Integrated acoustic resonators in commercial fin field-effect transistor technology

Abstract

In radio communication, the growth of beamforming and multiple-input–multiple-output technologies, which increase transceiver complexity, have led to a drive to reduce the size, weight and power of radio components by integrating them into a single system on chip. One approach is to integrate the frequency references of acoustic microelectromechanical systems (MEMS) with complementary metal–oxide–semiconductor processes, typically through a MEMS-first or MEMS-last approach that requires process customization. Here we report unreleased acoustic resonators that are fabricated in 14 nm fin field-effect transistor technology and operate in the X-band frequency range (8–12 GHz). The devices use phononic waveguides for acoustic confinement and exploit metal–oxide–semiconductor capacitors and transistors to electromechanically drive and sense acoustic vibrations. Fifteen device variations are analysed across 30 bias points, quantifying the importance of phononic confinement on resonator performance and demonstrating the velocity-saturated piezoresistive effect in active resonant transistors. Our results illustrate the feasibility of integrating acoustic devices directly into standard complementary metal–oxide–semiconductor processes.

Main

There is currently an increased focus on the functional diversification of existing semiconductor process nodes to create new technologies^1,2. This approach increases performance, supply chain resilience and security by reducing the number of chips from different process technologies that must be integrated and packaged into the final product. For technologies such as the fifth generation of wireless communications technology, such innovation is necessary to enable high-performance adaptable radios, where high-frequency resonators are a key element in both filters and voltage-controlled oscillators used. Recent developments in this area include thin-film bulk acoustic resonators with ferroelectric materials, as well as high-frequency Lamb- and Lamé-wave resonators using piezoelectric lithium niobate or aluminium nitride thin films^3,4,5,6.

To address band congestion, multiple-input–multiple-output arrays are becoming increasingly common as a way to multiplex transmissions between users in the same band, with large arrays allowing for increased performance across end users sharing the spectrum⁷. The beamforming enabled by such an antenna array is of particular use for higher-frequency bands, where propagation conditions are less stable due to increased radio-frequency (RF) absorption. These RF front ends require many more analogue components to be integrated in a compact form factor, driving research in RF integration into traditional digital processes.

Many high-performance technologies require integration using microelectromechanical systems (MEMS)-first or MEMS-last process schemes^8,9,10, which provide space and power savings compared with off-chip RF integration. The use of phononic-crystal (PnC) confinement, however, could allow resonator integration directly into a standard complementary metal–oxide–semiconductor (CMOS) process, potentially leading to larger multiple-input–multiple-output arrays in a smaller footprint at lower power^11,12. In addition to reducing parasitics from routing high-frequency signals over long distances, this also provides the opportunity to use high-performance transistors for active transduction, leading to potentially enhanced performance. Such an approach also provides a route to future acoustic coupling between devices co-located on the same chip, which reduces the need for power-hungry phase-locked loops and allows scaled coupled oscillator systems for neuromorphic computing to be explored^13,14,15,16. In this Article, we report CMOS fin field-effect transistor (FinFET)-based resonators that utilize acoustic waveguiding confinement operating in the Institute of Electrical and Electronics Engineers (IEEE) X-band of 8–12 GHz.

Resonator cavity design

The designed resonator structure, referred to as a fin resonant body transistor (fRBT) (Fig. 1), is fully integrated in the GlobalFoundries 14LPP commercial process and occupies a space of 9 μm × 15 μm (ref. ¹⁷). The device is a four-port network, differentially driven between adjacent gates along the fin length with the output of the resonator taken as the differential transconductance (equation (1)), which is a function of three main items: the electrical-to-acoustic transduction efficiency in the drive transistors, acoustic energy confinement and amplification in the resonance cavity, and acoustic-to-drain current conversion in the output transistors. The first of these items, namely, drive transduction, is electrostatic due to the 14 nm fabrication process used, although the potential exists for future piezoelectric drive using CMOS-compatible thin-film ferroelectrics^4,18,19. The third item, namely, acoustic-to-drain current conversion, is also largely a function of the process and materials used in device fabrication. Although this conversion will be examined utilizing a simplified model, the initial device design is focused on maximizing the acoustic energy confinement by varying the gate length, termination scheme and back-end-of-line (BEOL) confinement conditions:

$${g}_{\mathrm{mdd}}=\frac{{i}_{\mathrm{d}}}{{v}_{\mathrm{d}}}={Y}_{\mathrm{dd}21}-{Y}_{\mathrm{dd}12}.$$

(1)

Fig. 1: Overview of FinFET resonator.

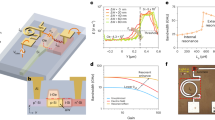
a, Cross-section of one period of the FinFET resonator, modelled in COMSOL, with the inset highlighting the Si fin (dark green) and epitaxial raised source and drain with silicide²⁰. The metal and contact layers are highlighted in orange and dark grey, respectively, and the dielectric layers are coloured blue and green. The target mode is primarily defined along the x direction (L_gate) via the 180°-phase constraint due to the differential drive and sense. b, Representative acoustic cavity, consisting of a sense block sandwiched between two drive blocks, with terminations at either end to increase acoustic confinement. A differential input is applied in the two drive blocks, with the output current taken from the sense transistors at the centre of the cavity. The grounded gates act as electrical isolation between the sense and drive blocks. c, Simulated target mode, with periodicity driven by L_gate, showing stress concentrated in the FinFET channel and confined by the BEOL metal layers. d, Experimentally measured mode, with f₀Q product of 8.2 × 10¹¹, placing it within an order of magnitude of the released MEMS resonators. e, Combined with a differential transconductance amplifier, the fRBT enables a high-frequency mechanically referenced two-phase oscillator in the standard CMOS process. Oscillator design considerations for active transduction resonators are presented elsewhere³⁹. f, Acoustically coupled (blue lines) network of oscillators in CMOS FEOL with local electrical clock routing (bronze lines), eliminating power-hungry phase-locked loops used for clock distribution. This could also enable scalable oscillatory computing for neuromorphic applications, directly interfacable with a classical CMOS circuit.

Figure 1a depicts a three-dimensional (3D) unit cell of the resonator with a 14-nm-wide FinFET at the front-end-of-line (FEOL) condition and periodically arranged metal blocks at the BEOL, categorized into Mx and Cx layers shown based on the thickness and minimum lateral feature sizes (Fig. 2a). The target resonant mode for the unreleased resonator is along the length direction of the fin transistors. To obtain a lower insertion loss and higher quality (Q) factor, the radiated acoustic energy needs to be concentrated at the metal–oxide–semiconductor capacitor drive transducers and sensing transistors. Compared with more traditional suspended resonators, this represents a challenge in the unreleased resonant body transistor design in commercial CMOS processes.

Fig. 2: BEOL acoustic confinement.

a, Representative unit cell for the simulated periodic PnC and plate structures (Mx 76-32 and Cx plates are shown), including the metal layer and interlayer dielectric (ILD) films present between each metal layer. The orange region represents the metal, whereas the surrounding layers are the dielectric. These structures extend throughout the width of the cavity (k_z = 0); hence, the band structure is shown over the irreducible Brillouin zone (IBZ) for a two-dimensional (2D) rectangular lattice, with x and y directions chosen to give the typical lattice points. Note that this swaps the y and z dimensions from the 3D device coordinates given in Fig. 1. The thickness of each layer is set by the process technology and varies between the Mx and Cx layers. b,c, Dispersion relationships for the 108 nm periodic PnC (b, utilized in L_gate = 106 nm devices with two PnC unit cells per device unit cell) along with the upper (Cx) metal layer of the 160 nm periodic PnC (c, utilized in all the unit cells). d–f, Dispersion relationship for Mx 130-60 PnCs (d, 190 nm periodic), utilized in L_gate = 80 nm devices, along with the Mx (e) and Cx (f) plate geometries. As expected, the plates show no complete bandgap over two dimensions, with propagation of the waveguided modes possible in the x direction. PnC arrangements, although exhibiting waveguided modes in the z direction, still have complete bandgaps in the x and y dimensions. Due to continuous translation symmetry in the plates, the periodicity (and hence the definition of periodic cell dimension a and point X) is somewhat arbitrary. The frequency at which these propagating modes reach the X point depends on the definition of X, with the dispersion relations in e and f corresponding to a width of 190 nm (for L_gate = 80 nm devices). Longer L_gate devices will have a smaller relative momentum and hence will reach the X point at lower frequencies, as evident from the dispersion relations in Fig. 4.

Integrating a PnC at the BEOL of the standard CMOS process and leveraging the mechanical bandgaps of such structures has proven to be an effective tool to confine the energy and boost the resonance Q factor^4,12. As shown by M1 in Fig. 3a, these periodic metals are uniform along the length (y direction) of the transistor gates (orthogonal to the fin direction) within the resonant cavity.

To study and optimize the bandgap induced by the PnCs, several 3D simulations were performed in COMSOL Multiphysics²⁰. Specifically, by mapping the real coordinates to reciprocal coordinates and searching for the eigenmodes along the first irreducible Brillouin zone in the 3D reciprocal lattice, a 130 × 60 nm² PnC (such as one that can be designed within the constraints of the Mx layers in the 14 nm process) yields a partial bandgap at the operating point (X) from 9.0 to 14.0 GHz (complete from 11.9 to 12.5 GHz; Fig. 2d). For the longer 106-nm-gate-length device, the design rules are such that a 76 × 32 nm² PnC can be utilized with two periods per unit cell. This smaller periodicity of PnC leads to complete bandgaps (Fig. 2b) from 8.7 to 9.9 GHz and from 12.3 to 14.6 GHz. At X, partial bandgaps exist from 8.2 to 12.0 GHz and from 12.0 to 14.6 GHz.

Fig. 3: Variations in resonant cavity design.

a, Top-down view of the device shows the central sense transistors with five pairs of capacitors on either side, allowing for a differential drive, capped on either end by termination (ten gates in the actual devices, abbreviated to three in the figure) and surrounded by a ground ring. The first-level metal M1 is used for routing within the structure, whereas higher-level metals in Mx and Cx (not shown for clarity in this diagram) rest above this routing in either the continuous plate or the PnC form. The Kx layer represents higher-level metal layers used for device-to-pad routing. b, Depiction of termination schemes investigated for use at the ends of the resonant cavity. c, View of a subset of the resonant cavity of devices A3 and A4, showing fins extending in the x direction and gates extending into the y direction. The RF drive signal is differentially applied, with alternating gates 180° out of phase. d, Variations in device design that were implemented and tested.

To further confine the elastic energy, a separate PnC designed under the design rules of the Cx metal layer is also considered for a subset of devices. The corresponding dispersion relationship is shown in Fig. 2c. A complete mechanical bandgap is then obtained between 8.7 and 9.8 GHz (a partial one from 9.8 to 11.8 GHz at X), which overlaps with the bandgap induced by the Mx metal PnC. Together, these PnC designs indicate that elastic waves with a frequency of 9–14 GHz propagating along the fin can be prohibited from propagating into the BEOL, with a subset of that frequency range experiencing a complete bandgap. For this reason, the devices are designed for a waveguided mode with a differential drive that exhibits a large momentum (k_x = π/a) at a frequency below the sound cone for the bulk silicon substrate, laterally confining the mode towards the driving/sensing transistors¹². When the design rules do not allow fine-pitched PnCs, continuous metal plates may be used as acoustic Bragg reflectors, although their translational symmetry in two dimensions can only lead to partial bandgaps (Fig. 2e,f)²¹.

Although the PnCs in the main resonant cavity enhance energy confinement and wave reflection from the BEOL, there also exists wave scattering at the two ends of the resonator. Reducing this scattering further increases the horizontal confinement, reduces the insertion loss, and hence increases the Q. The adiabatic theorem in photonic-waveguide design is leveraged here, which states that when the wave is propagated down the waveguide, scattering vanishes because of the limitation of sufficiently slow perturbation²¹. Therefore, the key to reduce this scattering is to introduce different units as terminations at the two ends for slower transitions. The unit cell for all the PnC structures in the major termination section throughout the paper is kept as 150 nm × 60 nm.

Although all the measured devices have ten terminating gates at each end of the cavity, two types of cavity termination spacing are explored to provide acoustic confinement in the lateral direction, namely, abrupt and gradual termination schemes (Fig. 3b). Abrupt termination refers to the scenario where a terminating periodic array with a constant pitch shifted from that of the resonance cavity array is immediately adjacent to the main resonance region. In this case, the gate length of the termination immediately transitions to the L_term value (Fig. 3d) and stays constant until the end of the device. As such, the guided waves are abruptly transitioned from the main cavity towards the ends. In the gradual termination scenario, the periodicity of the main resonant cavity adiabatically transitions from L_gate to the periodicity of the terminating array (L_term), resulting in a termination gate length gradually transitioning from 80 to 140 nm. This serves to reduce scattering from the two ends and boost Q (ref. ¹²).

FinFET active sensing

To understand the conversion from stress to drain current in the sense transistors, the modulation of three separate FET properties is examined: oxide capacitance, channel mobility due to piezoresistivity, and silicon bandgap. For ease of visualization, an initial analysis is performed with the source-referenced simplified strong-inversion model with α = 1 (the traditional ‘square-law model’ or SPICE level 1)²²:

$${I}_{\mathrm{d0}}=\mu_0 {C}_{\mathrm{ox}0}\frac{W}{L}\left(({V}_{\mathrm{GS}}-{V}_{\mathrm{T}}){V}_{\mathrm{DS}}-\frac{{V}_{\mathrm{DS}}^{2}}{2}\right),$$

(2)

where I_d is the drain current; μ is the carrier mobility; C_ox is the gate capacitance; V_DS and V_GS are the drain-to-source and gate-to-source bias, respectively; W and L are the channel width and length, respectively; and V_T is the threshold voltage required for substantial channel conduction.

This model has only a handful of parameters to describe the device operation, as opposed to the more advanced BSIM model commonly used in industry (Supplementary Information), which includes many empirically fit parameters to give the best device models for commercial applications²³. Additional information on the methods to simulate fRBTs in BSIM using a commercial process design kit is provided elsewhere²⁴.

Capacitance modulation in these devices is the same mechanism used in the electrostatic drive of these devices, except that rather than directly sensing the gate current, the capacitance modulation is being amplified through transistor action into a change in drain current. The piezoresistive effect, where the semiconductor carrier mobility is modulated through stress in the transistor channel, similarly appears as a multiplier on the transistor drain current. Modulation of semiconductor bandgap, on the other hand, largely affects the threshold voltage of the transistor. Supplementary Section 1 provides a complete derivation of these effects. Modified to include the effects of stress on μ, C_ox and V_T (modelled as μ(σ) = μ₀ + Δμ), the original expression for current in the linear region becomes the following:

$$\begin{array}{lll}{I}_{\mathrm{d}}(\sigma )&=&\left({\mu }_{0}{C}_{\mathrm{ox}0} +{\mu }_{0}{{\Delta }}{C}_{\mathrm{ox}} +{C}_{\mathrm{ox}0} {{\Delta }}\mu +{{\Delta }}\mu {{\Delta }}{C}_{\mathrm{ox}} \right)\\ && \times \frac{W}{L}\left(({V}_{\mathrm{GS}}-{V}_{\mathrm{T}0}){V}_{\mathrm{DS}}-\frac{{V}_{\mathrm{DS}}^{2}}{2}\right)\\ && -{{\Delta }}{V}_{\mathrm{T}}{V}_{\mathrm{DS}}\frac{W}{L}\left({\mu }_{0}{C}_{\mathrm{ox}0} \right. \\ && +\left. {\mu }_{0}{{\Delta }}{C}_{\mathrm{ox}} +{C}_{\mathrm{ox}0} {{\Delta }}\mu +{{\Delta }}\mu {{\Delta }}{C}_{\mathrm{ox}} \right),\end{array}$$

(3)

where

$$\begin{array}{lll}{{\Delta }}{I}_{\mathrm{d}}(\sigma )&=&({\mu }_{0}{{\Delta }}{C}_{\mathrm{ox}} +{C}_{\mathrm{ox}0} {{\Delta }}\mu +{{\Delta }}\mu {{\Delta }}{C}_{\mathrm{ox}} ) \\ && \times \frac{W}{L}\left(({V}_{\mathrm{GS}}-{V}_{\mathrm{T}0}){V}_{\mathrm{DS}}-\frac{{V}_{\mathrm{DS}}^{2}}{2}\right)\\ &&-{{\Delta }}{V}_{\mathrm{T}}{V}_{\mathrm{DS}}\frac{W}{L}\left({\mu }_{0}{C}_{\mathrm{ox}0} +{\mu }_{0}{{\Delta }}{C}_{\mathrm{ox}} \right. \\ && +\left. {C}_{\mathrm{ox}0} {{\Delta }}\mu +{{\Delta }}\mu {{\Delta }}{C}_{\mathrm{ox}} \right).\end{array}$$

(4)

Similarly, in saturation,

$${I}_{\mathrm{d}0}=\mu_0 {C}_{\mathrm{ox}0}\frac{W}{2L}\left({({V}_{\mathrm{GS}}-{V}_{\mathrm{T}})}^{2}\left(1+\lambda [{V}_{\mathrm{DS}}-({V}_{\mathrm{GS}}-{V}_{\mathrm{T}0})]\right)\right),$$

(5)

where λ represents the channel-length modulation coefficient (typically, 0.05 to 0.25) and

$$\begin{array}{lll}{{\Delta }}{I}_{\mathrm{d}}&=&({\mu }_{0}{{\Delta }}{C}_{\mathrm{ox}} +{C}_{\mathrm{ox}0} {{\Delta }}\mu +{{\Delta }}\mu {{\Delta }}{C}_{\mathrm{ox}} ) \\ && \times \frac{W}{2L}\left({({V}_{\mathrm{GS}}-{V}_{\mathrm{T}})}^{2}(1+\lambda ({V}_{\mathrm{DS}}-{V}_{\mathrm{GS}}+{V}_{\mathrm{T}}))\right)\\ &&-\frac{W}{2L}({\mu }_{0}{C}_{\mathrm{ox}0}+{\mu }_{0}{{\Delta }}{C}_{\mathrm{ox}}+{C}_{\mathrm{ox}0}{{\Delta }}\mu +{{\Delta }}\mu {{\Delta }}{C}_{\mathrm{ox}})\\ && \left[\right.{{\Delta }}{V}_{\mathrm{T}}\left[\lambda {({V}_{\mathrm{GS}}-{V}_{\mathrm{T}0})}^{2}-2({V}_{\mathrm{GS}}-{V}_{\mathrm{T}0})\times \right.\\ && \left. \left(1+\lambda \left[{V}_{\mathrm{DS}}-({V}_{\mathrm{GS}}-{V}_{\mathrm{T}0})\right]\right)\right]\\ && +{{\Delta }}{V}_{\mathrm{T}}^{2}\left[\left(1+\lambda \left[{V}_{\mathrm{DS}}-({V}_{\mathrm{GS}}-{V}_{\mathrm{T}0})\right]\right)-2\lambda ({V}_{\mathrm{GS}}-{V}_{\mathrm{T}0})\right]\\ && + \left.{{\Delta }}{V}_{\mathrm{T}}^{3}[\lambda ]\right]\end{array}.$$

(6)

For modern submicron devices, carriers do not exhibit constant mobility, but rather undergo velocity saturation at high fields. A simplified way to analytically model this is through a piecewise equation involving the saturation field (E_sat) and lateral field (E_x) in the direction of carrier motion as

$${v}_{\mathrm{d}}=\left\{\begin{array}{l}\frac{\mu | {E}_{x}| }{1+| {E}_{x}| /{E}_{\mathrm{sat}}}\,\,,\,\,| {E}_{x}| < {E}_{\mathrm{sat}}\quad \\ {v}_{\mathrm{sat}},\,\,| {E}_{x}| > {E}_{\mathrm{sat}}\quad \end{array}\right.,$$

(7)

which, solved at v_d = v_sat, gives

$${E}_{\mathrm{sat}}=\frac{2{v}_{\mathrm{sat}}}{\mu }$$

(8)

and leads to a modified expression for drain current, namely,

$${I}_{\mathrm{d}0}=\left\{\begin{array}{l}\mu_0 {C}_{\mathrm{ox}0}\frac{W}{L}\frac{1}{1+\frac{{V}_{\mathrm{DS}}}{{E}_{\mathrm{sat}}L}}\left(({V}_{\mathrm{GS}}-{V}_{\mathrm{T}}){V}_{\mathrm{DS}}-\frac{{V}_{\mathrm{DS}}^{2}}{2}\right)\,\,,\,\,{V}_{\mathrm{DS}} < {V}_{\mathrm{DSsat}}\quad \\ \quad \\ {C}_{\mathrm{ox}0}W{v}_{\mathrm{sat}0}\frac{{({V}_{\mathrm{GS}}-{V}_{\mathrm{T}})}^{2}}{({V}_{\mathrm{GS}}-{V}_{\mathrm{T}})+{E}_{\mathrm{sat}}(L-{{\Delta }}L)},\,\,{V}_{\mathrm{DS}} > {V}_{\mathrm{DSsat}}\quad \end{array}\right.,$$

(9)

where

$${V}_{\mathrm{DSsat}}=\frac{({V}_{\mathrm{GS}}-{V}_{\mathrm{T}}){E}_{\mathrm{sat}}L}{({V}_{\mathrm{GS}}-{V}_{\mathrm{T}})+{E}_{\mathrm{sat}}L}.$$

(10)

An important nuance for acoustic resonators is that both saturation velocity and change in mobility (piezoresistive effect) are related to the change in carrier effective mass caused by the acoustic deformation of the crystal lattice—saturation velocity by m*^−1/2 and mobility by a factor between m*^−1/2 and m*^−5/2 depending on doping (Supplementary Section 2 provides a detailed analysis). This relation means that although d.c. may saturate, the a.c. piezoresistive effect can still change the drain current to an extent, even in the saturation region. For this reason, a compound model is utilized that incorporates velocity saturation in the calculation of direct drain current but allows mobility to freely vary for a.c. calculations. Under this approach, the contribution to RF output from both electrostatic forces and mobility modulation should scale linearly with the drain current. The contribution from any threshold-voltage shift is seen to be related to drain bias only in the linear regime and is scaled by the impact of mobility and capacitance changes. In the saturation regime, on the other hand, the threshold-voltage shift is primarily a function of gate bias and is modified by drain bias only through channel-length modulation. These expressions for ΔI_d represent one half of the device transfer function g_mdd (equation (1)), with the other half being given by the voltage-to-strain conversion and subsequent strain confinement/resonance. Although the direct measurement of strain in the solid-state resonator in FEOL poses a challenge, all three of these aspects are subsequently investigated using the measured electrical results.

Analysis of design variations

The d.c. results, shown as an example for the 80-nm-gate-length device (A1; Supplementary Section 6), indicate that the sense transistors in all the devices were working as intended. The large current values of approximately 2 mA when the gate and drain are biased at V_dd are due to the parallel d.c. connection of the two sense transistors and large effective width of the individual transistors, where 40 fins span the resonant cavity (in the y direction) and are electrically connected in parallel.

Although the d.c. results were similar for all the devices (outside the expected differences due to gate-length variations), resonance-mode confinement was highly dependent on the design variations studied. A comparison of their differential transconductance spectra are shown in Fig. 4 along with the dispersion relations of the 80 and 106 nm devices with Mx PnC and Cx plates. From these data, it is evident that PnC confinement in the Mx layers results in a significantly improved Q factor and maximum transconductance. An offset in resonant frequencies between the simulated and experimental devices shows the challenge in simulating commercial CMOS devices, where a plethora of materials and complex geometries introduce opportunities for simulation error. Also visible is the role that the type of termination has in defining the centre frequency of nearby spurious modes in the device. This is not easily studied in simulation due to the computational intensity of simulating the full structure, highlighting the importance of experimental design splits in optimizing the performance.

Fig. 4: Experimental comparison of resonator designs.

a, Simulated dispersion relation of 80- and 106-nm-gate-length unit cells with Mx PnC and Cx plates (A3–A6). The regions of Mx and Cx modes are shaded in red, corresponding to the propagating mode shown in Fig. 2f. This is shifted down in frequency for the longer-gate-length device due to the smaller absolute momentum at the X point. Additional modes along reciprocal lattice vector ΓX (Supplementary Fig. 4) are caused by the finite number of metal layers in the device unit cell, unlike the infinite periodicity assumed in the BEOL simulation. Modes with high-elastic-energy percentage confined in the silicon fin (Supplementary Fig. 5) are highlighted for both devices. As expected from the simulations of BEOL confinement schemes, the 106 nm device with Mx 76-32 PnC shows fewer BEOL waveguided modes. b, Experimentally measured differential transconductance (0 dBm, V_drain = 0.8 V, V_gate = 0.8 V and V_drive = 0.8 V), separated by devices with Mx PnC (top) and Mx plates (bottom). Despite the discrepancy in absolute frequency, the simulated relative frequency offset between the modes and across the devices matches well with the experiment. The sudden increase in resonance frequency for the L_gate = 200 nm device may indicate that a harmonic mode is being driven, with the first-order mode falling below the range of confined frequencies.

Analysis of variance (ANOVA) was used to quantify the impact of these variations in device design on the spectrum of acoustic modes. Such an analysis including several modes does not give an exact value for mode frequency, Q factor or amplitude, but rather compares the average value that might be expected based on the selected design parameters. This analysis indicates an increased average transconductance in gradual transition devices (352 nS) versus abruptly terminated ones (302 nS), with a corresponding increase in the average Q factor (32 versus 24, respectively). In addition to this enhancement, the average resonance centre frequency was shown to slightly decrease from 11.29 to 11.16 GHz, driven by the downward shift in the left-most peak of the high-Q cluster of modes seen in PnC-confined devices.

The investigation of PnC confinement showed no significant change in the centre frequency of the modes, but it did show significantly improved average transconductance (204, 379 and 451 nS) and Q factor (20, 38 and 44, respectively) with increasing layers of PnC confinement. These trends are highlighted in Supplementary Fig. 10 along with an example of the peak-fitting results used for parameter extraction.

A comparison between the 80- and 106-nm-gate-length devices showed increasing average mode frequency at shorter gate lengths (11.66 versus 10.71 GHz, respectively), as expected given that this alters the resonator unit-cell dimensions. The complete ANOVA results are provided in Supplementary Table 1, where the centre frequency, Q factor and height of the resonant peaks in g_mdd are compared for the three design splits.

As the device with the highest performance, resonator A2 was selected for further analysis, with the maximum transconductance of the 11.75 GHz mode examined as a function of device biasing. This was done at a drive bias of V_dd, as g_mdd was seen to linearly increase with the increase in metal–oxide–semiconductor capacitance at higher drive bias (Supplementary Section 6). The dependence of g_mdd on sense transistor biasing (Fig. 5) highlights that device transconductance, as expected, is modulated in a manner consistent with piezoresistive and bandgap modulation. Although the transistor parameters are of the correct order of magnitude in the reported data fit, they slightly vary from real-world values due to the simplified model used. For example, the square-law model does not accurately capture the subthreshold (accumulation and weak inversion) behaviour, and thus, the fit favours a slightly lower V_T to more closely fit the bias currents near zero. This, in turn, leads to an overestimation of current at higher biases, which is compensated by a lower than expected value for mobility and a slightly larger equivalent oxide thickness. On the a.c. side, the fit is hindered by the presence of a noise floor in the S-parameter measurements that may obscure the lower peak levels. This, along with the poor near-threshold characteristics of the square-law model, contributes to the fitting error at lower values of g_mdd. Future devices incorporating ferroelectric drive capacitors would mitigate this issue by greatly increasing the efficiency of electromechanical conversion²⁵ and hence boosting the vibration amplitude and/or lowering power consumption. Moving away from the square-law model to a more advanced model such as that derived in another work²⁶ that captures all the regions of operation may decrease this error. Similarly, adopting band-structure simulations of silicon as a result of acoustic deformation could provide a unified source of mobility and threshold-voltage changes in the transistor, at the expense of increased computational requirements.

Fig. 5: Bias dependence of active sensing.

a, Simulated contributions to ΔI_d from bandgap modulation (threshold voltage), piezoresistive modulation (mobility), electrostatic modulation (oxide capacitance) and cross-term. For short-channel devices that are constrained by supply voltage, bandgap and piezoresistive modulation are of similar magnitudes and dominate over the electrostatic terms. b, These two terms, along with the overall drain current modulation, are plotted against the d.c. bias current of the sense transistor (x axis) for the simulated (top) and experimental (bottom) devices. The gate bias is shown by the marker colour (blue to yellow) and ranges from 0.0 to 0.8 V in steps of 0.1 V. The drain bias is represented by the marker size, moving from small to large as the bias increases from 0.0 to 0.8 V in steps of 0.1 V. The large cluster of points with equal gate biases and similar drain currents indicate saturation-mode operation for those bias conditions with channel-length modulation. The mobility term is linear with drain current, whereas the threshold-voltage term due to bandgap modulation has both a flat region (i) in the linear regime with no V_GS dependence for constant V_DS and a slight V_DS dependence (ii) for constant V_GS in the saturation regime. The experimental data roughly show a linear dependence of drain current on gate voltage (a hallmark of velocity saturation²² versus the ${V}_{\mathrm{GS}}^{2}$ dependence of the long-channel model). Some deviation between the model fit and experimental results can be seen at high drain bias and low gate bias, which may be indicative of mobility degradation due to vertical fields, which is not currently modelled. Additionally, the fit becomes worse when approaching the subthreshold, due to the abrupt cutoff in the drain current at V_T in the square-law model. Otherwise, the experimental results show a similar shape to that of the simulated device, indicating the dominance of both piezoresistive and bandgap modulation in the experimental resonator. c, Model fit to the experimental results (μ = 50 cm² V^–1 s^–1; equivalent oxide thickness, 1.2 nm; V_T = 0.24 V; v_sat =2.72 × 10⁷ cm s^–1; λ = 0.24; W = 3.9 µm; total stress, 0.97 MPa). A basin-hopping algorithm is used to find a global minimum fit for the d.c. transistor parameters, which are then fixed for the a.c. fit achieved by varying the stress.

For n-type metal–oxide–semiconductor devices oriented in the <110> direction, the negative piezoresistive coefficients ensure that the contribution of threshold-voltage shift and mobility is additive. If fRBT devices are implemented with p-type metal–oxide–semiconductor devices or in processes with different fin orientations, care should be taken to ensure that the dominant stress-dependent effects do not compete with each other. This may not be as much of an issue for long-channel resonant body transistor devices, as piezoresistive modulation dominates for long-channel devices that are not constrained by the supply voltage.

The highest-magnitude peak fit occurred in device A2 (L_gate = 80 nm, gradually terminated, dual PnC) at 11.73 GHz with a differential transconductance of 4.49 μS and Q = 69.8, for an f × Q product of 8.19 × 10¹¹ at drain, gate and drive biases of 0.6, 0.8 and 0.8 V, respectively. Although previously demonstrated unreleased resonators in the 32 nm silicon-on-insulator (SOI) process have achieved an f × Q product of 3.8 × 10¹³ with phononic confinement at 3.3 GHz, these 14 nm devices exhibit 50 times higher transconductance and show an almost three times improvement in Q over a similar frequency-measured mode in 32 nm SOI devices^27,28. Compared with some contemporary resonators in the X-band and adjacent K_u-band (12–18 GHz; Table 1), the unreleased devices in this work achieve moderate f × Q in an area smaller than comparable released devices. This, combined with the fact that the devices are integrated in the FEOL of a commercial CMOS technology node, opens the door for tight logic integration with minimum routing (and associated parasitics). Additional optimizations to the PnC and termination, although challenging due to process design rules, may further boost the Q factor of these devices. Furthermore, the incorporation of PnC confinement in longer gate lengths would enable this enhanced performance to be achieved across the IEEE X-band.

Table 1 Comparison with contemporaneously reported X-band and K_u-band (8–18 GHz) resonators

Conclusions

We have reported unreleased resonant fin transistors fabricated in standard 14 nm FinFET technology. An analytical model was developed that predicts resonator performance across sense transistor biasing conditions, using a combined velocity-saturated current at d.c. and unsaturated mobility variation at a.c. This highlights how the acoustic perturbation of carrier effective mass simultaneously modulates the saturation velocity and mobility. PnC confinement, which was experimentally shown to be the most important parameter in improving the unreleased resonator performance (an improvement on average of 2.2 times), provides a considerable opportunity for integrating acoustic devices into standard CMOS platforms. Our highest performing resonator—a gradually terminated 80-nm-gate-length device with both Mx and Cx PnC confinement—exhibits a transconductance amplitude of 4.49 μS and Q of 69.8, in the 11.73 GHz mode, resulting in an f × Q product of 8.2 × 10¹¹. This technology—combined with advances in CMOS-compatible ferroelectric and piezoelectric thin films—could be used to develop compact, low-cost, CMOS-integrated and electrically controllable resonators that require no additional packaging.

Characterization methods

Device measurement

An overview of the entire data pipeline is depicted in Supplementary Fig. 6. This process begins with S-parameter measurements taken at room temperature and pressure, with an input power of –10 dBm using an Agilent Technologies N5225a PNA instrument, with biasing provided by three Keithley 2400 source measure units (Supplementary Fig. 7). All the four devices were connected via General Purpose Interface Bus and synchronized via published Python3 scripts^29,30. WinCal XE 4.7 software (FormFactor) was used to facilitate the pre-measurement calibration, and hybrid Line-Reflect-Reflect-Match-Short-Open-Load-Reciprocal calibration was performed using an impedance standard substrate (ISS 129-246). Infinity ground–signal–signal–ground probes were used to allow for a compact biasing scheme, saving die real estate at the expense of increased cross-talk between the adjacent signal lines. Gate bias for the sense transistors was provided via a separate d.c. needle probe.

Measurement data post-processing

The acquired Touchstone files were first analysed using scikit-rf, which was used to perform open de-embedding and transform the single-ended parameters collected into their mixed-mode equivalent matrices³¹. From these, g_mdd was extracted to allow for the analysis of the designed differential mode. The magnitude of g_mdd for each sample at a bias of V_drain = 0.6 V, V_gate = 0.8 V and V_drive = 0.8 V was modelled as a collection of Gaussian peaks and fit via Lmfit using the Levenberg–Marquardt algorithm with initial guesses for frequency and peak height provided via user input through matplotlib’s ginput method³². These preliminary fits were then used as the initial conditions for the remainder of the 450 collected measurements taken at drain biases of 0.2, 0.4 and 0.6 V; drive biases of 0, 0.2, 0.4, 0.6 and 0.8 V; and sense FET gate biases of 0 and 0.8 V, These were again fit via Lmfit and parallelized using Dask³³. Due to the noisy nature of the data, with varying spectra between devices, a number of constraints were added to improve the fitting accuracy over all the design variations. The fitting was weighted by the g_mdd amplitude to emphasize the primary peaks over smaller spurious modes and background noise. Variation in peak standard deviation between the biases was constrained to two times the original standard deviation, reflecting the fact that Q is a function of the physical mode confinement. The centre frequency for each sample was constrained to a maximum of 5% deviation as a function of bias to improve the fitting accuracy and reflect the fact that mode shape—and thus the frequency of operation—again is primarily dictated by device geometry and not biasing.

Design variation analysis

The extracted peak properties were analysed in SAS JMP Pro 14 statistical discovery software to investigate the relationship between the splits in device design and variation in performance as a function of device bias³⁴. Before the analysis was carried out, high-error peak fits were eliminated (mean square error, >0.025; ≈5% of the data overall). The device splits (Fig. 2) are not entirely orthogonal due to a variety of constraints in device design related to the PnCs and gate lengths. Thus, one-way ANOVA was used on subsets of the experimental devices rather than trying to fit a multidimensional model to the entire sample set. To increase the number of statistical samples (and thus the chance of significance), all the bias combinations for each device were included in the analysis. For termination, this process is straightforward as there exists an abrupt and gradually terminated copy of every device, resulting in a comparison of all the devices. To investigate PnC confinement, the analysis was limited to designs with 80 nm gate length (A1–A4 and B0–B1) and the confinement treated as a three-level categorical factor.

Compared with the other factors studied, L_gate is unique in that it is the primary design variable for selecting the centre frequency due to the mode being defined by source/drain spacing. This means that the different values studied dramatically change the cavity shape and thus all the peaks detected in the studied frequency span of 9.5–13.5 GHz cannot be used in the analysis, as they are not present in this range in all the devices. To overcome this, a much smaller comparison of A3 and A4 (L_gate = 80 nm) to A5 and A6 (L_gate = 106 nm) was performed using only the prominent modes with transconductance above 500 nS and Q above 25 that were present towards the centre of the spectra. The downside of this approach is that the gate length is confounded with a change in Mx PnC design that is necessary for the different device geometries due to challenges in design rules. Despite this, the fact that the confinement method showed no significant change in centre frequency for 80 nm devices points towards this shift being dominated by gate length, as expected.

Transistor modelling

The examination of expected device performance using the derived analytical model was performed in Python. The contribution for each of the three components (bandgap, mobility and capacitance modulation) was taken as the difference between the positive- and negative-stress components. Lmfit was used to perform the optimization routine, using a basin-hopping algorithm to find a global minimum for d.c. The fit of g_mdd was performed using the Levenberg–Marquardt algorithm. The simplified one-dimensional model of a 3D transistor led to substantial cross-correlation between the stress directional components; however, the magnitude of the total stress remained relatively constant across the fit iterations.