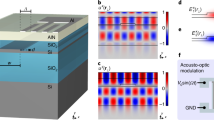
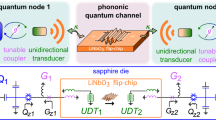
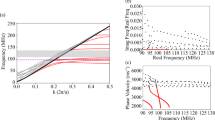
Abstract
Acoustic waves at microwave frequencies are widely used in wireless communication and are potential information carriers in quantum applications. However, most acoustic devices are passive components, and the development of phononic integrated circuits is limited by the inability to control acoustic waves in a low-loss, scalable manner. Here we report the electrical control of gigahertz travelling acoustic waves at room temperature and millikelvin temperatures. We achieve phase modulation by tuning the elasticity of a lithium niobate acoustic waveguide via the electro-acoustic effect. This phase modulator is then used to build an acoustic frequency shifter based on serrodyne phase modulation, and phase modulators in a Mach–Zehnder interferometer configuration are used to create an electro-acoustic amplitude modulator. By tailoring the phase matching between acoustic and quasi-travelling electric fields, we achieve reconfigurable non-reciprocal modulation with a non-reciprocity of over 40 dB. To illustrate the potential of the approach in quantum applications, we show that our electro-acoustic modulator can provide coherent modulation of single-phonon-level acoustic waves at 50 mK.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are provided with the paper. Other data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Campbell, C. Surface Acoustic Wave Devices and their Signal Processing Applications (Academic Press, 1989).
Chu, Y. et al. Quantum acoustics with superconducting qubits. Science 358, 199–202 (2017).
Manenti, R. et al. Circuit quantum acoustodynamics with surface acoustic waves. Nat. Commun. 8, 975 (2017).
Satzinger, K. J. et al. Quantum control of surface acoustic-wave phonons. Nature 563, 661–665 (2018).
Arrangoiz-Arriola, P. et al. Resolving the energy levels of a nanomechanical oscillator. Nature 571, 537–540 (2019).
Bienfait, A. et al. Phonon-mediated quantum state transfer and remote qubit entanglement. Science 364, 368–371 (2019).
Andersson, G., Suri, B., Guo, L., Aref, T. & Delsing, P. Non-exponential decay of a giant artificial atom. Nat. Phys. 15, 1123–1127 (2019).
Gustafsson, M. V. et al. Propagating phonons coupled to an artificial atom. Science 346, 207–211 (2014).
Whiteley, S. J. et al. Spin–phonon interactions in silicon carbide addressed by Gaussian acoustics. Nat. Phys. 15, 490–495 (2019).
Maity, S. et al. Coherent acoustic control of a single silicon vacancy spin in diamond. Nat. Commun. 11, 193 (2020).
Jiang, W. et al. Efficient bidirectional piezo-optomechanical transduction between microwave and optical frequency. Nat. Commun. 11, 1166 (2020).
Shao, L. et al. Microwave-to-optical conversion using lithium niobate thin-film acoustic resonators. Optica 6, 1498–1505 (2019).
Eggleton, B. J., Poulton, C. G., Rakich, P. T., Steel, M. J. & Bahl, G. Brillouin integrated photonics. Nat. Photon. 13, 664–677 (2019).
Forsch, M. et al. Microwave-to-optics conversion using a mechanical oscillator in its quantum ground state. Nat. Phys. 16, 69–74 (2020).
MacCabe, G. S. et al. Nano-acoustic resonator with ultralong phonon lifetime. Science 370, 840–843 (2020).
Hann, C. T. et al. Hardware-efficient quantum random access memory with hybrid quantum acoustic systems. Phys. Rev. Lett. 123, 250501 (2019).
Pechal, M., Arrangoiz-Arriola, P. & Safavi-Naeini, A. H. Superconducting circuit quantum computing with nanomechanical resonators as storage. Quantum Sci. Technol. 4, 015006 (2018).
Dahmani, Y. D., Sarabalis, C. J., Jiang, W., Mayor, F. M. & Safavi-Naeini, A. H. Piezoelectric transduction of a wavelength-scale mechanical waveguide. Phys. Rev. Appl. 13, 024069 (2020).
Hatanaka, D., Mahboob, I., Onomitsu, K. & Yamaguchi, H. Phonon waveguides for electromechanical circuits. Nat. Nanotechnol. 9, 520–524 (2014).
Fang, K., Matheny, M. H., Luan, X. & Painter, O. Optical transduction and routing of microwave phonons in cavity-optomechanical circuits. Nat. Photon. 10, 489–496 (2016).
Mayor, F.M. et al. Gigahertz Phononic Integrated Circuits on Thin-Film Lithium Niobate on Sapphire. Phys. Rev. Applied 15, 014039 (2021).
Fu, W. et al. Phononic integrated circuitry and spin-orbit interaction of phonons. Nat. Commun. 10, 2743 (2019).
Yang, Y., Lu, R., Gao, L. & Gong, S. 10–60-GHz electromechanical resonators using thin-film lithium niobate. IEEE Trans. Microw. Theory Techn. 68, 5211–5220 (2020).
Shao, L. et al. Non-reciprocal transmission of microwave acoustic waves in nonlinear parity–time symmetric resonators. Nat. Electron. 3, 267–272 (2020).
Mansoorzare, H. & Abdolvand, R. Acoustoelectric non-reciprocity in lithium niobate-on-silicon delay lines. IEEE Electron Device Lett. 41, 1444–1447 (2020).
Hackett, L. et al. Towards single-chip radiofrequency signal processing via acoustoelectric electron–phonon interactions. Nat. Commun. 12, 2769 (2021).
Bandhu, L. & Nash, G. R. Controlling the properties of surface acoustic waves using graphene. Nano Res. 9, 685–691 (2016).
Liang, B., Guo, X. S., Tu, J., Zhang, D. & Cheng, J. C. An acoustic rectifier. Nat. Mater. 9, 989–992 (2010).
Fleury, R., Sounas, D. L., Sieck, C. F., Haberman, M. R. & Alù, A. Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science 343, 516–519 (2014).
Walker, E. et al. Nonreciprocal linear transmission of sound in a viscous environment with broken P symmetry. Phys. Rev. Lett. 120, 204501 (2018).
Devaux, T., Cebrecos, A., Richoux, O., Pagneux, V. & Tournat, V. Acoustic radiation pressure for nonreciprocal transmission and switch effects. Nat. Commun. 10, 3292 (2019).
Xu, H., Jiang, L., Clerk, A. A. & Harris, J. G. E. Nonreciprocal control and cooling of phonon modes in an optomechanical system. Nature 568, 65–69 (2019).
Nomura, T. et al. Phonon magnetochiral effect. Phys. Rev. Lett. 122, 145901 (2019).
Zhu, D. et al. Integrated photonics on thin-film lithium niobate. Adv. Opt. Photon. 13, 242–352 (2021).
Cho, Y. & Yamanouchi, K. Nonlinear, elastic, piezoelectric, electrostrictive, and dielectric constants of lithium niobate. J. Appl. Phys. 61, 875–887 (1987).
Shao, L. et al. Phononic band structure engineering for high-Q gigahertz surface acoustic wave resonators on lithium niobate. Phys. Rev. Appl. 12, 014022 (2019).
De, S. K. & Aluru, N. R. Theory of thermoelastic damping in electrostatically actuated microstructures. Phys. Rev. B 74, 144305 (2006).
Tabrizian, R., Rais-Zadeh, M. & Ayazi, F. Effect of phonon interactions on limiting the f.Q product of micromechanical resonators. 2009 International Solid-State Sensors, Actuators and Microsystems Conference (TRANSDUCERS 2009), 2131-2134.
Ekström, M. K. et al. Surface acoustic wave unidirectional transducers for quantum applications. Appl. Phys. Lett. 110, 073105 (2017).
Zheng, L., Wu, D., Wu, X. & Lai, K. Visualization of surface-acoustic-wave potential by transmission-mode microwave impedance microscopy. Phys. Rev. Appl. 9, 061002 (2018).
Zheng, L., Shao, L., Loncar, M. & Lai, K. Imaging acoustic waves by microwave microscopy: microwave impedance microscopy for visualizing gigahertz acoustic waves. IEEE Microw. Mag. 21, 60–71 (2020).
Kurizki, G. et al. Quantum technologies with hybrid systems. Proc. Natl. Acad. Sci. USA 112, 3866–3873 (2015).
Fu, W. et al. Cavity electro-optic circuit for microwave-to-optical conversion in the quantum ground state. Phys. Rev. A 103, 053504 (2021).
Acknowledgements
We thank C. Wang and C. Chia for fruitful discussion. This work is supported by the US Navy Office of Naval Research (ONR) QOMAND grant no. N00014-15-1-2761, DOE HEADS-QON grant no. DE-SC0020376, National Science Foundation (NSF) grant no. DMR-2004536, the Welch Foundation Grant F-1814 and NSF RAISE/TAQS grant no. NSF ECCS-1839197. N.S. is supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) and the AQT Intelligent Quantum Networks and Technologies (INQNET) research programme. D.Z. is supported by the Harvard Quantum Initiative (HQI) postdoctoral fellowship and A*STAR Science and Engineering Research Council (SERC) Central Research Fund (CRF). L.S. is supported by the Virginia Tech Foundation.
Author information
Authors and Affiliations
Contributions
L.S.: conceptualization, methodology, investigation, formal analysis, visualization, writing (original draft). D.Z.: methodology, investigation, writing (original draft). M.C.: investigation, writing (review and editing). D.L.: investigation, writing (review and editing). N.S.: methodology, investigation, writing (original draft). Y.H.: writing (review and editing). P.T.R.: writing (review and editing). K.L.: resources, methodology, writing (review and editing, and supervision). K.K.B.: resources, writing (review and editing, and supervision). M.L.: resources, writing (review and editing, and supervision).
Corresponding authors
Ethics declarations
Competing interests
M.L. is involved in developing LN technologies at HyperLight Corporation. President and Fellows of Harvard College has a patent pending (Application number: PCT/US21/60426) on the electro-acoustic modulators, in which M.L. and L.S. are listed as inventors. The other authors declare no competing interests.
Peer review
Peer review information
Nature Electronics thanks Anton Kockum and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Simulated acoustic phase velocities for varying directions on X-cut LN.
The direction is defined by the angle respective to the crystal Z axis. The electromechanical coupling coefficient \(k^2 = 2\;(v_o - v_m)/v_o\), where vo and vm are the phase velocities when the top surface is free and electrically shorted, respectively. The direction of the waveguide used in our device is 30°, as indicated by the dash line.
Extended Data Fig. 2 Measured transmission spectra of the acoustic modulator at temperatures of 300 and 1.3 K.
The results indicate a 25 dB improvement in peak transmission at low temperature. The frequency shift of the spectrum is due to the temperature dependent elasticity of LN.
Extended Data Fig. 3 Measured Peak-to-peak acoustic phase changes due to sinusoidal modulating signals of varying peak-to-peak voltage (Vpp) at room and cryogenic temperatures.
The sinusoidal modulating signals are of the frequency fmod =10 kHz. Linear fits show Vπ of 53 V at room temperature (300 K) and 135 V at 1.3 K, respectively. The same device is measured as that in Fig. 2.
Extended Data Fig. 4 Modulation bandwidth of the 1-cm-long electro-acoustic phase modulator.
The modulation efficiency is indicated by the first sideband power due to the phase modulation. The measured 3-dB bandwidth is 110 kHz. The modulation approaches zero at fmod = 336 kHz when the acoustic traveling time through the modulator equals 1/fmod. The same device is measured as that in Fig. 2.
Extended Data Fig. 5 Fifty millikelvin measurement setup.
The electro-acoustic modulator is mounted on a mixing plate of a dilution fridge with a base temperature below 50 mK. The input microwave signal is provided by a signal generator and, to ensure negligible contribution of thermal noise, passed through attenuators at various temperature stages of the fridge before going into our device. The output microwave signal from the modulator passes through a circulator, a high-electron-mobility transistor (HEMT) amplifier at 4 K, two low-noise amplifiers at room temperature, and is finally detected by a real-time spectrum analyzer (RSA). The modulation signal is provided by a function generator. A controlled and thermally isolated thermal source, which consists of a heater, temperature sensor, and a 30 dB attenuator, is installed in the microwave line before our electro-acoustic modulator to calibrate the gain and added noise in the output/readout line.
Extended Data Fig. 6 Noise measurement of the electro-acoustic modulator at 50 mK.
Total noise power spectrum density near fc when (1) no signal is applied to the electro-acoustic modulator (black), (2) only the carrier microwave signal is applied (blue), and (3) both the carrier microwave and modulation signals are applied (red). The total noise power \(N_{tot} = N_{dev} + N_{add}\), where Ndev is the noise of the electro-acoustic modulator and Nadd is the added noise from the readout chain. Nadd is mainly determined by the high-electron-mobility transistor (HEMT) at the 4 K stage. The electro-acoustic modulation adds negligible noise and is thus suitable for quantum phononics. The same device is measured as that in Fig. 2. The error bars indicate the standard deviation of measured noise power spectrum density.
Extended Data Fig. 7 Phase matching between a traveling acoustic wave and a quasi-traveling electric field.
The modulation sideband power is measured with varied modulation frequency and phase delay between the three electrodes. The maximum modulations that satisfy the phase matching condition are indicated by the red line. The condition for the maximum nonreciprocity in phase modulation is indicated by the black dots, as the counter propagating acoustic waves experience opposite phase delays compared to the propagating waves. The sideband power is normalized to the unmodulated carrier acoustic wave power. The measured date is from the same device as in Figs. 4C and 4D, which consists of three electrodes with overall modulation length of 1 cm.
Supplementary information
Supplementary Video 1
Principle of non-reciprocal acoustic phase modulation. The first (last) 30 s depict a wavefront of the acoustic wave as a blue (red) dot travelling in the forward (backward) direction. The top window illustrates three electrodes of the modulator (labelled as V1, V2 and V3) that have sinusoidal signals applied that are 120° out of phase with each other. The bottom window depicts the signals in the time domain, depicting the electrode regions for each signal. The middle window indicates the phase accumulation experienced by the wavefront as it propagates through the modulator.
Source data
Source Data Fig. 1
Source data for plots.
Source Data Fig. 2
Source data for plots.
Source Data Fig. 3
Source data for plots.
Source Data Fig. 4
Source data for plots.
Source Data Extended Data Fig. 1
Source data for plots.
Source Data Extended Data Fig. 2
Source data for plots.
Source Data Extended Data Fig. 3
Source data for plots.
Source Data Extended Data Fig. 4
Source data for plots.
Source Data Extended Data Fig. 6
Source data for plots.
Source Data Extended Data Fig. 7
Source data for plots.
Rights and permissions
About this article
Cite this article
Shao, L., Zhu, D., Colangelo, M. et al. Electrical control of surface acoustic waves. Nat Electron 5, 348–355 (2022). https://doi.org/10.1038/s41928-022-00773-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41928-022-00773-3
This article is cited by
-
Acoustic resonances in non-Hermitian open systems
Nature Reviews Physics (2023)
-
Multi-beam ultrafast laser processing of free-standing nanofilms
Applied Physics A (2023)
-
Electrical control of quantum acoustics
Nature Electronics (2022)