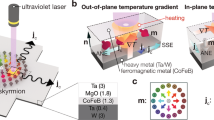
Abstract
The efficient generation, manipulation and detection of magnetic skyrmions are important for the development of future spintronic devices. One approach is to use electric-current-induced spin torques. Recently, thermally induced skyrmion motion has also been observed, but wider experimental evidence and its capabilities remain limited. Here we report the thermal generation, manipulation and thermoelectric detection of nanoscale skyrmions in microstructured metallic multilayers integrated with on-chip heaters. The local application of heat can facilitate a domain morphological transition and the formation of skyrmions at the device edge, where a low energy barrier exists. We observe the unidirectional diffusion of skyrmions from hot regions to cold regions, which is due to the interplay among the repulsive forces between skyrmions, thermal spin–orbit torques, entropic forces and magnonic spin torques. The thermally generated skyrmions can also be electrically detected via the Nernst voltage.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots in this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Yu, X. Z. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Jonietz, F. et al. Spin transfer torques in MnSi at ultralow current densities. Science 330, 1648–1651 (2010).
Fert, A., Cros, V. & Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 8, 152–156 (2013).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013).
Bogdanov, A. N. & Rößler, U. K. Chiral symmetry breaking in magnetic thin films and multilayers. Phys. Rev. Lett. 87, 037203 (2001).
Heinze, S. et al. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 7, 713–718 (2011).
Romming, N. et al. Writing and deleting single magnetic skyrmions. Science 341, 636–639 (2013).
Jiang, W. et al. Blowing magnetic skyrmion bubbles. Science 349, 283–286 (2015).
Chen, G., Mascaraque, A., N'Diaye, A. T. & Schmid, A. K. Room temperature skyrmion ground state stabilized through interlayer exchange coupling. Appl. Phys. Lett. 106, 242404 (2015).
Woo, S. et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 15, 501–506 (2016).
Moreau-Luchaire, C. et al. Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature. Nat. Nanotechnol. 11, 444–448 (2016).
Fert, A., Reyren, N. & Cros, V. Magnetic skyrmions: advances in physics and potential applications. Nat. Rev. Mater. 2, 17031 (2017).
Everschor-Sitte, K., Masell, J., Reeve, R. M. & Klaui, M. Perspective: magnetic skyrmions—overview of recent progress in an active research field. J. Appl. Phys. 124, 240901 (2018).
Jiang, W. et al. Skyrmions in magnetic multilayers. Phys. Rep. 704, 1–49 (2017).
Mochizuki, M. et al. Thermally driven ratchet motion of a skyrmion microcrystal and topological magnon Hall effect. Nat. Mater. 13, 241–246 (2014).
Everschor, K. et al. Rotating skyrmion lattices by spin torques and field or temperature gradients. Phys. Rev. B 86, 054432 (2012).
Zázvorka, J. et al. Thermal skyrmion diffusion used in a reshuffler device. Nat. Nanotechnol. 14, 658–661 (2019).
Bauer, G. E. W., Saitoh, E. & van Wees, B. J. Spin caloritronics. Nat. Mater. 11, 391–399 (2012).
Koshibae, W. & Nagaosa, N. Creation of skyrmions and antiskyrmions by local heating. Nat. Commun. 5, 5148 (2014).
Lin, S. Z., Batista, C. D., Reichhardt, C. & Saxena, A. AC current generation in chiral magnetic insulators and skyrmion motion induced by the spin Seebeck effect. Phys. Rev. Lett. 112, 187203 (2014).
Lemesh, I. et al. Current-induced skyrmion generation through morphological thermal transitions in chiral ferromagnetic heterostructures. Adv. Mater. 30, 1805461 (2018).
Kovalev, A. A. & Tserkovnyak, Y. Thermoelectric spin transfer in textured magnets. Phys. Rev. B 80, 100408 (2009).
Kong, L. Y. & Zang, J. D. Dynamics of an insulating skyrmion under a temperature gradient. Phys. Rev. Lett. 111, 067203 (2013).
Wild, J. et al. Entropy-limited topological protection of skyrmions. Sci. Adv. 3, e1701704 (2017).
Shiomi, Y., Kanazawa, N., Shibata, K., Onose, Y. & Tokura, Y. Topological Nernst effect in a three-dimensional skyrmion-lattice phase. Phys. Rev. B 88, 064409 (2013).
Seki, S., Yu, X. Z., Ishiwata, S. & Tokura, Y. Observation of skyrmions in a multiferroic material. Science 336, 198–201 (2012).
Kézsmárki, I. et al. Néel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8. Nat. Mater. 14, 1116 (2015).
Legrand, W. et al. Hybrid chiral domain walls and skyrmions in magnetic multilayers. Sci. Adv. 4, eeat0415 (2018).
Li, W. et al. Anatomy of skyrmionic textures in magnetic multilayers. Adv. Mater. 31, 1807683 (2019).
Muller, J., Rosch, A. & Garst, M. Edge instabilities and skyrmion creation in magnetic layers. New J. Phys. 18, 065006 (2016).
Bottcher, M., Heinze, S., Egorov, S., Sinova, J. & Dupe, B. B–T phase diagram of Pd/Fe/Ir(111) computed with parallel tempering Monte Carlo. New J. Phys. 20, 103014 (2018).
Yan, P., Wang, X. S. & Wang, X. R. All-magnonic spin-transfer torque and domain wall propagation. Phys. Rev. Lett. 107, 177207 (2011).
Zhang, X. C. et al. Skyrmion-skyrmion and skyrmion-edge repulsions in skyrmion-based racetrack memory. Sci. Rep. 5, 7643 (2015).
Jiang, W. et al. Direct observation of the skyrmion Hall effect. Nat. Phys. 13, 162–169 (2017).
Litzius, K. et al. Skyrmion Hall effect revealed by direct time-resolved X-ray microscopy. Nat. Phys. 13, 170–175 (2017).
Chumak, A. V., Vasyuchka, V. I., Serga, A. A. & Hillebrands, B. Magnon spintronics. Nat. Phys. 11, 453–461 (2015).
Rohart, S. & Thiaville, A. Skyrmion confinement in ultrathin film nanostructures in the presence of Dzyaloshinskii-Moriya interaction. Phys. Rev. B 88, 184422 (2013).
Bessarab, P. F. et al. Lifetime of racetrack skyrmions. Sci. Rep. 8, 3433 (2018).
Lin, S.-Z. Edge instability in a chiral stripe domain under an electric current and skyrmion generation. Phys. Rev. B 94, 020402(R) (2016).
Tomasello, R. et al. Micromagnetic understanding of the skyrmion Hall angle current dependence in perpendicularly magnetized ferromagnets. Phys. Rev. B 98, 224418 (2018).
Schlickeiser, F., Ritzmann, U., Hinzke, D. & Nowak, U. Role of entropy in domain wall motion in thermal gradients. Phys. Rev. Lett. 113, 097201 (2014).
Kim, D. J. et al. Observation of transverse spin Nernst magnetoresistance induced by thermal spin current in ferromagnet/non-magnet bilayers. Nat. Commun. 8, 1400 (2017).
Zeissler, K. et al. Discrete Hall resistivity contribution from Néel skyrmions in multilayer nanodiscs. Nat. Nanotechnol. 13, 1161–1166 (2018).
Maccariello, D. et al. Electrical detection of single magnetic skyrmions in metallic multilayers at room temperature. Nat. Nanotechnol. 13, 233–237 (2018).
Kanazawa, N. et al. Discretized topological Hall effect emerging from skyrmions in constricted geometry. Phys. Rev. B 91, 041122 (2015).
Scarioni, A. F. et al. Thermoelectric signature of individual skyrmions. Preprint at https://arxiv.org/pdf/2001.10251 (2020).
Nayak, A. K. et al. Magnetic antiskyrmions above room temperature in tetragonal Heusler materials. Nature 548, 561 (2017).
Yu, X. Z. et al. Transformation between meron and skyrmion topological spin textures in a chiral magnet. Nature 564, 95–98 (2018).
Das, S. et al. Observation of room-temperature polar skyrmions. Nature 568, 368–372 (2019).
Acknowledgements
Work carried out at Tsinghua was supported by the Basic Science Center Project of NSFC (grant no. 51788104), the National Key R&D Program of China (grant nos. 2017YFA0206200 and 2016YFA0302300), the National Natural Science Foundation of China (grant no. 11774194, 51831005, 1181101082 and 11804182), Beijing Natural Science Foundation (grant no. Z190009), Tsinghua University Initiative Scientific Research Program and the Beijing Advanced Innovation Center for Future Chip (ICFC). The work at LANL was carried out under the auspices of the US Department of Energy (DOE) NNSA under contract no. 89233218CNA000001 through the Laboratory Directed Research and Development (LDRD) Program and was supported by the Center for Nonlinear Studies at LANL. This research used resources of the Advanced Light Source, a U.S. DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. K.-S.L. acknowledges support from the National Research Foundation (NRF) of Korea grant funded by the Korean government (MSIT) (2019K1A3A7A09033400 and 2019R1A2C2002996). M.-Y.I. acknowledges support from the NRF of Korea funded by the Ministry of Education, Science and ICT (2018K1A4A3A03075584 and 2016M3D1A1027831), DGIST R&D program of the Ministry of Science, ICT and Future Planning (18-BT-02) and support by Lawrence Berkeley National Laboratory through the LDRD Program. W.H. acknowledges support from the National Natural Science Foundation of China (no. 11574006). R.T. and G.F. thank the ‘ThunderSKY’ project funded from the Hellenic Foundation for Research and Innovation (HFRI) and the General Secretariat for Research and Technology (GSRT) under grant no. 871. We thank N. Nagaosa, M. Garst, J. Zang, X. Zhang, G. Yu and Y. Wang for fruitful discussions.
Author information
Authors and Affiliations
Contributions
W.J. conceived the idea and designed the experiments. H.Z. and T.X. fabricated the thin film. Z.W., H.Z., L.Z., Y.D. and C.S. performed lithographic processing. Z.W. did the COMSOL Multiphysics simulation. M.G., H.B. and H.W. did the anomalous Nernst measurements. Y.Y., H.Z. and W.H. carried out the ferromagnetic resonance experiments. S.L. performed the atomistic micromagnetic simulation and Fokker–Planck calculation. R.T. and G.F. performed the layer-dependent micromagnetic simulations. M.C. and G.F. implemented the micromagnetic solver for multilayer calculations. Z.W., S.J., W.C., H.H., S.L., K.L., M.I. and W.J. performed the full-field, soft X-ray microscopy imaging experiments and data analysis. W.J. and S.L. wrote the manuscript with inputs from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Skyrmion generation and propagation in the [Ta/Co20Fe60B20/MgO]15 multilayer by using the lower heater.
At opposite magnetic fields, by applying pulse voltages (duration fixed at 100 μs) into the lower heater (H2), thermal generation of skyrmions, together with their subsequent propagation towards the cold side (upper side) are realized.
Extended Data Fig. 2 Skyrmion generation and propagation in the [Ta/Co20Fe60B20/MgO]15 multilayer at positive magnetic fields (+μ0H⊥) by using the upper heater.
At different positive magnetic fields, by applying pulse voltages (duration fixed at 100 μs) into the upper heater (H1), the thermal generation of skyrmions, together with the propagation towards the cold side are evident. The experimentally utilized parameters and the estimated temperatures at the upper edge (hot side) are also listed.
Extended Data Fig. 3 Domain morphological transition in the [Ta/Co20Fe60B20/MgO]15 multilayer at smaller magnetic fields by using the upper heater.
At smaller (positive/negative) magnetic fields and by applying pulse voltages (duration fixed at 100 μs) into the upper heater, thermally induced domain morphological transition is observed.
Extended Data Fig. 4 Skyrmion generation and propagation in the [Ta/Co20Fe60B20/MgO]15 multilayer by changing the pulse duration via the upper heater.
By increasing the duration of pulse voltages (amplitude is fixed at Vh= 0.526 V) in the upper heater, thermal generation of skyrmions and their propagation towards the cold side (lower edge) are observed.
Extended Data Fig. 5 Skyrmion generation and propagation in the [Pt/Co60Fe20B20/MgO/Ta]15 multilayer by using the upper heater.
At opposite magnetic fields, by applying increased amplitudes of pulse voltages (duration fixed at 300 μs) into the upper heater, thermal generation of skyrmions, together with their subsequent propagation towards the cold side are realized.
Extended Data Fig. 6 The phase diagram of skyrmion generation at different pulse durations in the [Ta/Co20Fe60B20/MgO]15 multilayer.
a, The response of competing magnetic phases to different pulse durations (with a fixed amplitude Vh = 0.526 V) and magnetic fields. b, The dependence of the maximum temperatures at the upper (hot) edge \(\left( {T_{{\mathrm{U}} - {\mathrm{E}}}^{\mathrm{S}}} \right)\) on the pulse duration (tpulse). The nonlinear increase of \({\mathrm{T}}_{{\mathrm{U}} - {\mathrm{E}}}^{\mathrm{S}}\) following the increase of pulse duration can be attributed to the fast dissipation of heat through substrate. c,d, Following the continuous increase of pulse duration above 4 ms, the system approaches thermal equilibrium with a constant temperature at the hot edge \(\left( {{\mathrm{T}}_{{\mathrm{U}} - {\mathrm{E}}}^{\mathrm{S}} = 496K} \right)\) (c) and a constant temperature gradient in the multilayer ∇T(x) = 1.3 K μm-1 (d).
Extended Data Fig. 7 Micromagnetic simulation results of transformation from stripe domains to densely packed skyrmion lattices driven by temperature gradients.
Following the increasing time, presented as the number of frames (1, 30, 100, 200, 300, 400), skyrmions are first nucleated at the hot edge, followed by the immediate thermal diffusion from the hot side towards the cold side. Meanwhile, skyrmions are also generated by breaking the stripe domains followed by relaxation in the hot side. The diffusion of skyrmions then pushes the stripe domains out of the simulation box. The time lapse between consecutive frames is \(\Delta t = 60J_{{\mathrm{ex}}}/\gamma D^2\). The temperature gradient is \(k = 0.01J_{{\mathrm{ex}}}/k_B\) and \({\it{H}}_a = 0.6{\it{D}}^2/{\it{J}}_{ex}\). Here we assume the film thickness is 0.1Jex/D. The scale bar is 20Jex/D. The open (periodic) boundary condition is used in the horizontal (vertical) direction.
Extended Data Fig. 8 Micromagnetic simulation results of the diffusion of skyrmions purely driven by temperature gradients.
The micromagnetic simulation of skyrmion diffusion in a nanowire geometry is performed by using the open boundary condition. First, skyrmions are thermally generated at high temperature side using a larger temperature gradient. Subsequently, the temperature gradient is reduced to avoid the nucleation of skyrmions at the hot side, which results in the diffusion of skyrmions towards the cold side. Some skyrmions exit the nanowire through the sample edge during the diffusion. The length and width of the nanowire are 120Jex/D and 40Jex/D, respectively. The thermal gradient for diffusion is k = 0.008Jex/kB. Disorders in spin anisotropy are introduced to suppress the magnonic spin torque by reducing the magnon mean free path. Here we assume the film thickness is 0.1Jex/D. The scale bar is 10Jex/D.
Extended Data Fig. 9 Anomalous Nernst effect measured under different temperature gradients in the [Ta/Co20Fe60B20/MgO]15 multilayer.
a, The evolution of anomalous Nernst voltages (VANE) measured with different currents supplied into the heater (IHeater). b, Following the increase of IHeater, a parabolic increase of saturated VANE(μ0H⊥ = 100mT) can be found. c, The evolution of VANE(μ0H⊥ = 100 mT) as a function of ∇T(x). d, The time evolution of VANE measured at a fixed IHeater = 3 mA and μ0H⊥ = 25 mT, after switching off skyrmion generation currents (from 3.5 mA to 6 mA in 0.5 mA steps). Upon removing the increased DC currents used for generating skyrmions, discretized steps are gradually resolved. e, The corresponding IHeater as a function of time used for the ANE measurement in d.
Supplementary information
Supplementary Information
The following parts are discussed here. Part 1. Magnetic measurements of [Ta/Co20Fe60B20/MgO]15 multilayer. Part 2. Layout of the integrated device. Part 3. Size determination of skyrmions in different multilayers. Part 4. Skyrmion generation in a bigger device made of the [Ta/Co20Fe60B20/MgO]15 multilayer. Part 5. Determination of the current-induced Oersted fields and damping parameters. Part 6. COMSOL simulation parameters and the temperature profiles of the device. Part 7. Thermal diffusion of a single skyrmion in the [Ta/Co20Fe60B20/MgO]15 multilayer. Part 8. Calibrations of temperatures and temperature gradients. Part 9. Estimate of the energy barrier by Monte Carlo simulations. Part 10. Energy barrier for the penetration of a skyrmion. Part 11. Transformation from stripe domain into skyrmions. Part 12. Details of the Fokker–Planck equation. Part 13. Estimation of the thermal spin torque and magnonic spin torque contributions. Part 14. Evaluation of the three-dimensional skyrmion profile with layer-resolved micromagnetic simulation studies.
Supplementary Video 1
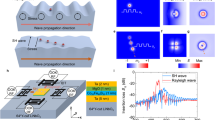
This video contains the whole set of raw images shown in Fig. 2a, where the morphological change from stripe domains to densely packed skyrmion lattice can be directly seen.
Supplementary Video 2
This video contains the whole set of raw images shown in Fig. 2b, where the generation of a skyrmion from the FM background and the subsequent motion of skyrmions from the hot region to the cold region is resolved.
Supplementary Video 3
This video contains the whole set of raw images shown in Fig. 2c for the [Pt/Co/Ta]15 multilayer, where the generation of skyrmions and their subsequent propagation can be seen.
Supplementary Video 4
This video contains the whole set of raw images shown in Fig. 3a; by applying an increasing temperature gradient, the diffusion of skyrmions can be identified.
Supplementary Video 5
This video corresponds to the micromagnetic simulation results shown in Fig. 3b, where the thermal generation of skyrmions from a pure FM background is fully reproduced.
Supplementary Video 6
This video corresponds to the micromagnetic simulation results shown in Extended Data Fig. 7, where the thermal generation of skyrmions from a stripe-domain phase is fully reproduced.
Supplementary Video 7
This video corresponds to the micromagnetic simulation results shown in Extended Data Fig. 8, where the diffusion and annihilation of skyrmions in the presence of smaller temperature gradients are reproduced.
Supplementary Video 8
This video corresponds to the Monte Carlo simulation results shown in the Supplementary Information Part 11.
Rights and permissions
About this article
Cite this article
Wang, Z., Guo, M., Zhou, HA. et al. Thermal generation, manipulation and thermoelectric detection of skyrmions. Nat Electron 3, 672–679 (2020). https://doi.org/10.1038/s41928-020-00489-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41928-020-00489-2
This article is cited by
-
Acoustic-driven magnetic skyrmion motion
Nature Communications (2024)
-
Ordered creation and motion of skyrmions with surface acoustic wave
Nature Communications (2023)
-
Heat current-driven topological spin texture transformations and helical q-vector switching
Nature Communications (2023)
-
Reversible writing/deleting of magnetic skyrmions through hydrogen adsorption/desorption
Nature Communications (2022)
-
Topology dependence of skyrmion Seebeck and skyrmion Nernst effect
Scientific Reports (2022)