Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Generalized parity–time symmetry condition for enhanced sensor telemetry

Nature Electronics volume 1, pages 297–304 (2018)Cite this article

Subjects

A Publisher Correction to this article was published on 24 May 2018

This article has been updated

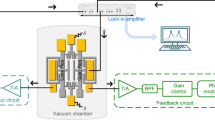
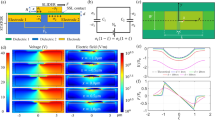
Abstract

Wireless sensors based on micromachined tunable resonators are important in a variety of applications, ranging from medical diagnosis to industrial and environmental monitoring. The sensitivity of these devices is, however, often limited by their low quality (Q) factor. Here, we introduce the concept of isospectral party–time–reciprocal scaling (PTX) symmetry and show that it can be used to build a new family of radiofrequency wireless microsensors exhibiting ultrasensitive responses and ultrahigh resolution, which are well beyond the limitations of conventional passive sensors. We show theoretically, and demonstrate experimentally using microelectromechanical-based wireless pressure sensors, that PTX-symmetric electronic systems share the same eigenfrequencies as their parity–time (PT)-symmetric counterparts, but crucially have different circuit profiles and eigenmodes. This simplifies the electronic circuit design and enables further enhancements to the extrinsic Q-factor of the sensors.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Non-Hermitian telemetric sensor system.
Fig. 2: MEMS-based wireless pressure sensor.
Fig. 3: Evolution of eigenfrequencies and reflection spectra as a function of the non-Hermiticity parameter γ and coupling strength κ.
Fig. 4: Pressure-induced spectral changes for conventional and PT-symmetric telemetric sensors.
Fig. 5: Evolution of the eigenfrequencies and reflection spectra for PTX-symmetric telemetric sensors.

Change history

  • 24 May 2018

    In the version of this Article originally published, a division symbol was mistakenly omitted from both of the y axis labels in Fig. 5a. The label in the left panel should have read ‘Re((ω×ω0)/2π) (MHz)’ and the label in the right panel should have read ‘Im((ω×ω0)/2π) (MHz)’. This has now been corrected.

References

  1. Nopper, R., Niekrawietz, R. & Reindl, L. Wireless readout of passive LC sensors. IEEE Trans. Instrum. Meas. 59, 2450–2457 (2010).

    Article  Google Scholar 

  2. Collins, C. C. Miniature passive pressure transensor for implanting in the eye. IEEE Trans. Biomed. Eng. 2, 74–83 (1967).

    Article  Google Scholar 

  3. Pozar, D. M. Microwave Engineering 4th edn (John Wiley & Sons, New York, 2012).

    Google Scholar 

  4. Mokwa, W. Medical implants based on microsystems. Meas. Sci. Technol. 18, R47–R57 (2007).

    Article  Google Scholar 

  5. Chavan, A. V. & Wise, K. D. Batch-processed vacuum-sealed capacitive pressure sensors. J. Micro. Syst. 10, 580–588 (2001).

    Article  Google Scholar 

  6. Chen, P. J., Rodger, D. C., Saati, S., Humayun, M. S. & Tai, Y. C. Microfabricated implantable parylene-based wireless passive intraocular pressure sensors. J. Micro. Syst. 17, 1342–1351 (2008).

    Article  Google Scholar 

  7. Chen, L. Y. et al. Continuous wireless pressure monitoring and mapping with ultra-small passive sensors for health monitoring and critical care. Nat. Commun. 5, 5028 (2014).

    Article  Google Scholar 

  8. Huang, H., Chen, P. Y., Hung, C. H., Gharpurey, R. & Akinwande, D. A zero power harmonic transponder sensor for ubiquitous wireless μL liquid-volume monitoring. Sci. Rep. 6, 18795 (2016).

    Article  Google Scholar 

  9. Yvanoff, M. & Venkataraman, J. A feasibility study of tissue characterization using LC sensors. IEEE Trans. Antenna Propagat. 57, 885–893 (2009).

    Article  Google Scholar 

  10. Bender, C. M. & Boettcher, S. Real spectra in non-Hermitian Hamiltonians having P T symmetry. Phys. Rev. Lett. 80, 5243 (1998).

    Article  MathSciNet  MATH  Google Scholar 

  11. Makris, K. G., El-Ganainy, R., Christodoulides, D. N. & Musslimani, Z. H. Beam dynamics in PT symmetric optical lattices. Phys. Rev. Lett. 100, 103904 (2008).

    Article  Google Scholar 

  12. Rüter, Ch. E. et al. Observation of parity–time symmetry in optics. Nat. Phys. 6, 192–195 (2010).

    Article  Google Scholar 

  13. Regensburger, A. et al. Parity–time synthetic photonic lattices. Nature 488, 167–171 (2012).

    Article  Google Scholar 

  14. Lin, Z. et al. Unidirectional invisibility induced by PT-symmetric periodic structures. Phys. Rev. Lett. 106, 213901 (2011).

    Article  Google Scholar 

  15. Mostafazadeh, A. Invisibility and PT symmetry. Phys. Rev. A 87, 012103 (2013).

    Article  Google Scholar 

  16. Longhi, S. PT-symmetric laser absorber. Phys. Rev. A 82, 031801 (2010).

    Article  Google Scholar 

  17. Chong, Y. D., Ge, L. & Stone, A. D. PT-symmetry breaking and laser-absorber modes in optical scattering systems. Phys. Rev. Lett. 106, 093902 (2011).

    Article  Google Scholar 

  18. Feng, L., Wong, Z. J., Ma, R. M., Wang, Y. & Zhang, X. Single-mode laser by parity-time symmetry breaking. Science 346, 972–975 (2014).

    Article  Google Scholar 

  19. Hodaei, H., Miri, M. A., Heinrich, M., Christodoulides, D. N. & Khajavikhan, M. Parity–time-symmetric microring lasers. Science 346, 975–978 (2014).

    Article  Google Scholar 

  20. Wong, Z. J. et al. Lasing and anti-lasing in a single cavity. Nat. Photon. 10, 796–801 (2016).

    Article  Google Scholar 

  21. Lee, J. M. et al. Reconfigurable directional lasing modes in cavities with generalized PT symmetry. Phys. Rev. Lett. 112, 253902 (2014).

    Article  Google Scholar 

  22. Peng, B. et al. Parity–time-symmetric whispering-gallery microcavities. Nat. Phys. 10, 394–398 (2014).

    Article  Google Scholar 

  23. Ramezani, H., Kottos, T., El-Ganainy, R. & Christodoulides, D. N. Unidirectional nonlinear PT-symmetric optical structures. Phys. Rev. A 82, 043803 (2010).

    Article  Google Scholar 

  24. Chang, L. et al. Parity-time symmetry and variable optical isolation in active-passive-coupled microresonators. Nat. Photon. 8, 524–529 (2014).

    Article  Google Scholar 

  25. Schindler, J., Li, A., Zheng, M. C., Ellis, F. M. & Kottos, T. Experimental study of active LRC circuits with PT symmetries. Phys. Rev. A 84, 040101 (2011).

    Article  Google Scholar 

  26. Schindler, J. et al. PT-symmetric electronics. J. Phys. A 45, 444029 (2012).

    Article  MATH  Google Scholar 

  27. Bender, N. et al. Observation of asymmetric transport in structures with active nonlinearities. Phys. Rev. Lett. 110, 234101 (2013).

    Article  Google Scholar 

  28. Fleury, R., Sounas, D. & Alù, A. An invisible acoustic sensor based on parity–time symmetry. Nat. Commun. 6, 5905 (2015).

  29. Lu, X. Y., Jing, H., Ma, J. Y. & Wu, Y. PT-symmetry-breaking chaos in optomechanics. Phys. Rev. Lett. 114, 253601 (2015).

    Article  Google Scholar 

  30. Xu, X. W., Liu, Y. X., Sun, C. P. & Li, Y. Mechanical PT symmetry in coupled optomechanical systems. Phys. Rev. A 92, 013852 (2015).

    Article  Google Scholar 

  31. Wiersig, J. Sensors operating at exceptional points: general theory. Phys. Rev. A 93, 033809 (2016).

    Article  Google Scholar 

  32. Chen, P. Y. & Jung, J. PT-symmetry and singularity-enhanced sensing based on photoexcited graphene metasurfaces. Phys. Rev. Appl. 5, 064018 (2016).

    Article  Google Scholar 

  33. Liu, Z. P. et al. Metrology with PT-symmetric cavities: enhanced sensitivity near the PT-phase transition. Phys. Rev. Lett. 117, 110802 (2016).

    Article  Google Scholar 

  34. Chen, W., Özdemir, Ş. K., Zhao, G., Wiersig, J. & Yang, L. Exceptional points enhance sensing in an optical microcavity. Nature 548, 192–196 (2017).

    Article  Google Scholar 

  35. Hodaei, H. et al. Enhanced sensitivity at higher-order exceptional points. Nature 548, 187–191 (2017).

    Article  Google Scholar 

Download references

Acknowledgements

This work has been supported by the NSF ECCS grant no. 1711409 (to P.-Y.C.), the Air Force Office of Scientific Research, the Welch Foundation with grant no. F-1802 (to A.A.) and the Army Research Office (ARO) grant no. W911NF-17-1-0481 (to R.E.-G.). Device fabrication was carried out in the Nano Fabrication Service Core (nFab) at the Wayne State University.

Author information

Authors and Affiliations

  1. Department of Electrical and Computer Engineering, Wayne State University, Detroit, MI, USA

    Pai-Yen Chen, Maryam Sakhdari, Mehdi Hajizadegan, Qingsong Cui & Mark Ming-Cheng Cheng

  2. Department of Physics and Henes Center for Quantum Phenomena, Michigan Technological University, Houghton, MI, USA

    Ramy El-Ganainy

  3. Department of Electrical and Computer Engineering, Michigan Technological University, Houghton, MI, USA

    Ramy El-Ganainy

  4. Advanced Science Research Center, City University of New York, New York, NY, USA

    Andrea Alù

  5. Graduate Center of the City University of New York, New York, NY, USA

    Andrea Alù

  6. Department of Electrical Engineering, City College of New York, New York, NY, USA

    Andrea Alù

Authors
  1. Pai-Yen Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Maryam Sakhdari
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mehdi Hajizadegan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Qingsong Cui
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Mark Ming-Cheng Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Ramy El-Ganainy
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Andrea Alù
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

M.S., M.H. and Q.C. designed the PT and PTX circuits and performed experimental measurements. M.S., M.H., Q.C. and M.C. designed and fabricated the MEMS pressure sensor. P.-Y.C., M.S. and M.C. conceived the experimental concepts. P.-Y.C., M.C., R.E.-G. and A.A. developed the concepts. P.-Y.C. and A.A. planned and directed the research. P.-Y.C., R.E.G. and A.A. wrote the manuscript.

Corresponding authors

Correspondence to Pai-Yen Chen or Andrea Alù.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Notes 1–3 and Supplementary Figures 1–10

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Chen, PY., Sakhdari, M., Hajizadegan, M. et al. Generalized parity–time symmetry condition for enhanced sensor telemetry. Nat Electron 1, 297–304 (2018). https://doi.org/10.1038/s41928-018-0072-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41928-018-0072-6

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing