Abstract
Solar-based water sanitation is an environmentally friendly process for obtaining clean water that requires efficient light-to-heat-to-vapour generation. Solar-driven interfacial evaporation has potential, but the inability to control interfacial evaporators for solar tracking limits efficiency at large solar zenith angles and when using optical concentration. Furthermore, clogging affects the efficiency of the device. Here, we create a super-wicking and super-light-absorbing (SWSA) aluminium surface for efficient solar-based water sanitation. The measured evaporation rate exceeds that of an ideal device operating at 100% efficiency, which we hypothesize resulted from a reduced enthalpy of vaporization within the microcapillaries. Limited solar absorber–water contact for water transport minimizes heat losses to bulk water and maximizes heat localization at the SWSA surface. The device can be mounted at any angle on a floating platform to optimize incident solar irradiance and can readily be integrated with commercial solar-thermal systems. With a design that is analogous to bifacial photovoltaic solar panels, we show a 150% increase in efficiency compared with a single-sided SWSA. Given the open capillary channels, the device surface can be easily cleaned and reused. Using the SWSA surface to purify contaminated water, we show a decrease in the level of contaminants to well below the WHO and EPA standards for drinkable water.
Similar content being viewed by others
Main
The combined effects of global warming, population increase, dietary changes, and competition over water resources have led to the growing global water crisis that threatens underdeveloped and developed countries1. In particular, the lack of access to clean and affordable water is a major obstacle for the development and health of 30% of the world’s population1. Although some regions have access to water, they lack access to safe and drinkable water. Sanitation of domestic and industrial wastewater would be a feasible and economically viable solution for reducing stress on groundwater resources and expenses on water imports2. To sanitize water, solar-based water disinfection is a viable and environmentally friendly solution. However, although solar-based water disinfection eliminates microbial pathogens and reduces diarrhoeal morbidity, it cannot sanitize water from other contaminants, such as heavy metals and industrial, domestic and agricultural pollutants2.
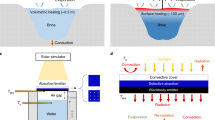
A solution to the global water sanitation crisis should realize efficient water sanitation with low cost materials, which should require low maintenance and should be universally viable to all types of contaminants. In a similar manner to the rain cycle, wastewater can be completely sanitized using solar energy for evaporating water and condensing vapour into drinkable water. Solar-thermal water-evaporation systems require a solar absorber that converts absorbed light to heat to evaporate water. Conventional solar-driven evaporation systems, which rely on bottom heating, suffer from low efficiency as heat is generated at the surface of the solar absorber, while evaporation occurs at the water–air interface, leading to unnecessary thermal losses3,4 (Fig. 1a). More recently, higher-efficiency solar-based water evaporation was demonstrated using the interfacial evaporation approach5 (Fig. 1b), whereby solar-thermal heat and vapour generation occur at the same location—that is, heat is localized at the absorber surface. The solar absorber is buoyant and floats on the water surface and water is delivered to the absorber using a porous substrate or hydrophilic fibres6,7. Furthermore, by adding thermally insulating material to the solar absorber, the heat loss to bulk water is further minimized8,9.
a, Solar-based water evaporation is traditionally realized using volumetric or bottom heating, in which heating and evaporation are spatially decoupled5. For a–d, the yellow arrows indicate sunlight. b, Solar-based interfacial heating overcomes the spatial-decoupling problem and maximizes the water-evaporation efficiency using buoyant light-absorber devices and by ensuring that water is transported to the solar absorber where heat is localized5. c, Interfacial heating using an SWSA surface ensures that water is transported to the solar absorber even if the device is not horizontally floating, which minimizes heat waste and renders the system mountable at any angle to directly face the Sun. d, A schematic comparing an SWSA sheet (left) and a conventional horizontally lying absorber surface (right). The SWSA enables it to operate at any angle to maximize the incident solar flux and the device efficiency when the Sun is at a large zenith angle. e, Water sanitation using light-absorbing porous materials with closed capillaries suffer from clogging over time (left). By contrast, using an open capillary architecture, similar to SWSA, the light-absorber surface can be easily cleaned with, for example, water spraying, and can be reused (right).
Although the previously demonstrated interfacial evaporation is efficient, it suffers from several drawbacks. The demonstrated devices generally use multiple layers to absorb light, wick water and thermally insulate the device to prevent dissipation of heat to bulk water, which makes the device relatively complex. Furthermore, interfacial evaporators have to float on the water horizontally and, therefore, cannot be mounted at different angles to face the Sun to optimize incident solar irradiance and are not compatible with well-matured solar tracking technologies. Accordingly, floating interfacial evaporators can be a part of solar stills as survivor kits10, but cannot be integrated with commercial solar-thermal systems5. Finally, the closed capillaries in porous wicking materials that are used to transport water suffer from clogging, which degrades the device efficiency5 and increases the maintenance cost. This problem was partially addressed in recent studies using a multi-layer solar evaporation structure for salt rejection only, but was not extended to other contaminants11,12. The clogging problem is particularly alarming in regard to solar-based water sanitation as a possible solution to the lack of clean water access in underdeveloped regions, where 35–50% of water projects are estimated to fail during the first 5 years owing to a lack of maintenance13. A real solution to the clean water crisis should therefore be easy to maintain and reuse with minimal operation costs. Moreover, tackling the global water shortage crisis requires a solution that can be integrated with large-scale solar-thermal technologies and that is mountable and compatible with solar tracking.
Here, we introduce a SWSA metal surface for water sanitation. The surface is made of single-step femtosecond-laser-treated aluminium (Al), where a burst of femtosecond (fs) laser pulses turns a normal, low-cost and shiny Al sheet into an SWSA surface. We demonstrate high-efficiency solar-based generation of water-vapour with evaporation rates exceeding that of an ideal device operating at 100% efficiency which we hypothesize is due to the reduced enthalpy of water vaporization (HLV) within the microcapillaries. Our super-wicking surface, on which water runs uphill against gravity at a steady-state speed of 2.1 mm s−1, directly delivers water to the solar absorber surface mounted at any angle. Accordingly, the SWSA sheet realizes interfacial heat localization with minimal contact with bulk water; there is therefore minimal heat loss (Fig. 1c). Furthermore, SWSA-based water evaporation reduces the complexity of the device; a thermally insulating layer6 and an additional wicking material14 are not necessary to realize high efficiencies. Although a floating aid using a buoyant material can add additional functionality to the SWSA-based sanitation device to self-manage water level5,6,9,15,16, the buoyant material is not necessary for the purpose of heat localization. The solar panel design of SWSA sheets enables them to be used as a solar-thermal panel for water sanitation as water transport to the solar absorber surface requires minimal contact with the water surface (Fig. 1d). The SWSA surface can be mounted at any angle to directly face the Sun to optimize available solar irradiance at the absorber surface to increase the device performance at large solar zenith angles. This is because, for a location at a zenith angle Θ, a Sun-faced solar receiver (Fig. 1d, left) collects more solar flux compared with a flat one (Fig. 1d, right) by a factor of (cosΘ)−1. The SWSA can therefore be integrated with commercial solar-thermal technologies to increase the total available solar flux for efficient vapour generation. In contrast to porous interfacial absorbers with closed capillary tubes that can suffer from clogging and salt precipitation (Fig. 1e, left), the SWSA has open capillary tubes that can be cleaned and reused from all types of contaminants without an additional salt/contaminant rejecting layer (Fig. 1e, right).
SWSA Al
The material used to realize super-wicking and super-light absorption should be widely available. Although Al is an abundant and cheap metal, it is highly reflective with no wicking properties. Using femtosecond laser processing (Supplementary Fig. 1), which we described previously17,18,19,20,21, a shiny Al sheet is converted to a super-light absorber (Fig. 2a) with a high hemispherical absorption of, on average, αλ ≈ 97% over the entire solar spectrum and ≈85% in non-solar region, demonstrating efficient absorption of solar and thermal radiation by the SWSA surface (Fig. 2b and Extended Data Fig. 1b). For solar-thermal technologies, angular insensitivity is highly desirable to operate a device efficiently, even when the Sun is at a wider azimuth angle during sunrise and sunset. Specular absorption measurement shows that our absorber has more than 97% absorbance for solar radiation up to 75° zenith angle for the Sun (Extended Data Fig. 1), which corresponds to sun hours from 05:56:41 to 17:53:32 at New York City (latitude, 40° 43′ 0″ N; longitude, 74° 01′ 05″ W) on summer month of 7 June 2017. By contrast, the total solar absorptance given by \(\alpha _{{\mathrm{solar}}} = G^{ - 1}\mathop {\int}\limits_0^\infty {\alpha _\lambda } \left( \lambda \right)G_\lambda \left( \lambda \right){\mathrm{d}}\lambda\) ≈ 92%, where G is the total solar irradiance, and Gλ is the spectral solar irradiance at a given wavelength λ. The SWSA surface consists of a hierarchical nano- and microstructures, with periodic microgrooves superimposed by finer nanoscale structures. The super-absorption comes from these hierarchical patterns. Figure 2c shows scanning electron microscopy (SEM) images of the SWSA Al surface at different scales, showing the hierarchical structures (Supplementary Figs. 2 and 3). Randomly formed Al nanoparticles during laser surface processing exhibit strong light absorption due to the excitation of localized plasmon resonances. The broad absorption band is due to the hybridization of the plasmon modes of randomly distributed nanoparticles with different sizes and shapes22,23. The microchannels in which the nanoparticles reside further trap the scattered light and enable efficient light absorption (Supplementary Figs. 4 and 5).
a, A photograph of an Al sheet that was processed using a femtosecond laser to render it SWSA. Scale bar, 10 mm. b, The optical absorption spectrum of an SWSA sheet for the wavelength range corresponding to the solar spectrum. c, SEM images of the SWSA sheet showing the hierarchical microstructures and nanostructures. From left to right, scale bars, 100 µm, 10 µm, and 200 nm. d, High-speed camera images of an SWSA sheet showing a water droplet wicking the SWSA surface. Scale bar, 5 mm. e, The water wet-front (Wwf) propagation versus time, fitted with a Washburn fit.
The microchannels act as capillary tubes in which a water droplet at the bottom of SWSA quickly springs uphill (Extended Data Fig. 2, Supplementary Videos 1 and 2))18,19,20 and the position of water wet front Wwf follows the Washburn–Rideal equation \(W_{{\mathrm{wf}}}^2 = {K}\left( {{\alpha }},{\theta} \right)\frac{{\gamma h}}{\mu }t\), where γ is the liquid surface tension, μ is the bulk liquid viscosity and K(α,θ) is a geometric term that depends on the groove angle α and the liquid/surface contact angle θ (ref. 24,25). Owing to K(α,θ) ∝ cosθ, the intrinsic hydrophilicity of Al enables the capillary action to take place due to the low water-Al contact angle. The capillary action is further enhanced due to the presence of micro/nanoparticles (Supplementary Fig. 6) that increase the surface roughness because cosθrough = r cosθ, where the roughness parameter r > 1 (ref. 26). To study the water wicking dynamics, we vertically mounted the sample surface then added a 200 µl water drop and used a high-speed camera to image Wwf progression over time (Fig. 2d and Extended Data Fig. 2, Supplementary Videos 1 and 2). Water runs uphill against gravity with initial speed of 6.5 cm s−1 and it reaches a steady-state speed of ~2.1 mm s−1 after wetting a sample with a height of 35 mm (Extended Data Fig. 2b,c). The results shown in Fig. 2e are well fitted by a classical Washburn fit and show that \(W_{{\mathrm{wf}}} \propto \sqrt t\). Water is pumped uphill on the SWSA surface at a rate of ~71.8 ± 7.15 mg s−1 (Supplementary Fig. 7).
Thermodynamics of water evaporation in the SWSA microcapillaries
The water-evaporation rate on an SWSA sheet and of bulk water with the same surface area (400 mm2) was measured simultaneously with no external heat input by placing both samples in a dark and controlled environment (temperature, 21 °C; room humidity, 33%). An equal sensible heat from ambient is available to the water at the SWSA surface and to the bulk water as the input thermal energy (Pin) for evaporation. As shown in Supplementary Fig. 9, the dark-condition evaporation rate from the SWSA surface is much larger than the bulk-water evaporation rate. The enhanced rate of water evaporation from the SWSA surface compared with the bulk water could be due to an increased mass transfer coefficient owing to a larger effective surface area at the water–air interface in the SWSA sheet and/or due to reduction in the HLV. The estimated value of the effective surface area at the water–air interface at the SWSA surface is 76.5 ± 0.5% of the area of the bulk water (Supplementary Fig. 8), ruling out the first possibility. Consequently, the reduction in HLV can be considered to be the possible reason behind the enhanced rate of vaporization from the SWSA surface. Our estimated value of HLV at the SWSA surface is 1,220 ± 19 kJ kg−1 (Supplementary Note 6), that is, approximately half of the bulk water value (2,440 kJ kg−1)27.
To understand the origin of the reduced HLV in the SWSA microcapillaries, we performed Raman spectroscopy analysis of bulk water and water confined in SWSA microcapillaries at room temperature (Supplementary Fig. 10). We showed that, owing to the molecular bonding of water with the SWSA surface, water molecules convert to a state with a higher number of hydrogen bonds, confirming the formation and activation of larger-size water clusters in the microcapillaries (Supplementary Notes 7 and 8, Supplementary Figs. 11–13). According to the water-cluster theory28,29, water molecules escape from the liquid-water surface to water-vapour either in the form of monomers or in large-sized water clusters. Bulk-water evaporation, where water molecules escape liquid-water surface in the form of monomers, requires that all hydrogen bonds to be broken. However, clustered evaporation requires that hydrogen bonds are broken only at the surface of the clusters. As a consequence, clustered evaporation has a lower HLV value compared with bulk-water evaporation. The hypothesis of reduced HLV is further supported by the presence of liquid water clusters in the vapour phase (Supplementary Fig. 14) and thermodynamic analysis of the phase transition of liquid water to water vapour (Supplementary Note 11, Supplementary Fig. 15).
Solar-based water evaporation using SWSA Al sheets
We first investigated the thermal leakage from the SWSA sheet to the bulk water. Figure 3a (left) shows a photograph of the vertically mounted SWSA sheet in contact with the water surface, and corresponding thermal image after illumination from a solar simulator at 1 Sun (1,000 W m−2; Fig. 3a, right). The temperature of the SWSA sheet was increased while the bulk water remained close to ambient temperature. Figure 3b shows the time evolution of the temperature of the SWSA sheet, the water surface and the bulk water. The results show that the heat dissipation to the bulk water was negligible (Supplementary Note 12). To measure the evaporation efficiency of the device, the SWSA sheet was attached to a piece of thermally insulating foam to float on the water surface and the entire setup was placed onto a digital scale to measure the water mass with time (Fig. 3c, Extended Data Fig. 3). The SWSA sheet was bent into a U shape and mounted on a thermally insulating foam to ensure a minimal contact with the contaminated water surface (Fig. 3c, top right; for schematic, and bottom right; actual photograph of the system). Note that we used this configuration for convenience to perform the evaporation measurements, that is, the SWSA sheet does not need a floating aid, as we discussed above, for the purpose of thermal insulation (Extended Data Fig. 4). The mass of water evaporated per unit area over time for various optical concentrations is shown in Fig. 3d with and without the SWSA sheet. In all cases, we subtracted the dark-condition evaporation rate to control for evaporation without solar irradiation6. The evaporation-rate slope changed over time until it reached an equilibrium state, which enabled us to determine the steady-state rate of mass loss \(\dot m\). For the case of water without the SWSA sheet (the bulk water evaporation), the equilibrium was reached after ~1,500 s, whereas, with the SWSA sheet, it was reached after only ~50 s. We note that, for different optical concentrations without introducing water, the average response time of the SWSA sheet τ90, that is, the time it takes for the sheet to reach 90% of its maximum temperature, was ~81 ± 7 s, and the average relaxation time τ10—that is, the time it takes for the temperature to drop up to 10% of its maximum value—was 103 ± 6 s (Extended Data Fig. 5).
a, A photograph of an SWSA sheet mounted vertically and brought into contact with the water surface (left), and the corresponding infrared thermal camera image after illumination with a solar simulator at an optical concentration of 1 Sun (right). b, Time evolution of the temperature of the SWSA sheet (black), water surface (red), and bulk water (blue). c, The experimental setup that was used to measure the solar water-evaporation efficiency of the device (left). The setup consists of an SWSA sheet that was floated on contaminated water using a thermally insulating foam. Light incident on the sample from a solar simulator is absorbed and water vapour is generated. The mass of generated vapour is measured using a balance. A schematic of a cross-sectional view (top right) and a photograph of the SWSA sheet on a thermally insulating foam floating on contaminated water at room temperature (bottom right) are shown. The thick grey arrows in the top-right panel show vapour transport direction, while the thin blue arrows show directions for the water transport. d, The measured change in the water mass (ΔM) due to evaporation over time for bulk water (solid lines) and an SWSA sheet (dashed lines) with the same interfacial area for COpt = 1, 3 and 5. e, The extracted mass evaporation rate for COpt = 1−5 for bulk water (blue triangles), SWSA (black dots) and an ideal device operating at 100% efficiency (red stars) showing the superior performance of the SWSA sheet. The error bars for each data point show the s.d. (SWSA and water) of the linear fitting of corresponding mass loss versus time curve, and the error bars in the optical concentration were obtained using the method described in Supplementary Note 13.
Furthermore, the evaporation rate for the SWSA sheet shows a 20-fold increase compared with that of bulk water at 3 Suns. From the water-evaporation data, it is customary to calculate the efficiency of steam generation (\(\eta = \dot mH_{{\mathrm{LV}}}/C_{{\mathrm{Opt}}}P_0\))4,6,9,23,27, where COpt is the optical concentration and P0 = 1,000 W m−2 is solar irradiance at 1 Sun. However, this criterion is inaccurate in conveying the device water-evaporation efficiency, as the HLV considerably decreases for water confined in SWSA microcapillaries, as described above. Reducing the HLV could decrease the efficiency of water evaporation but, eventually, it will increase the evaporation rate—that is, the end goal of water sanitation. Accordingly, the energy-efficiency formula penalizes a device that efficiently reduces the HLV and increases the water-evaporation rate. To provide an accurate description of the device evaporation efficiency, we compared \(\dot m\) from the SWSA sheet with the evaporation rate of an ideal device operating at 100% efficiency with bulk water HLV,bulk, that is, a perfect absorber with no radiation, conduction or convection losses9 (Fig. 3e). The obtained \(\dot m\) from our device (black dots) was higher than an ideal device (red stars) for all COpt ≥ 2. Moreover, the effective empirical value of HLV, when used in the efficiency formula, makes the efficiency numbers plausible.
The dependence of the device performance on COpt is due to the importance of water transport management in the solar-driven water-evaporation process. For a given capillary dimension and orientation, the water transport rate through the capillaries \(\left( {\dot m_{{\mathrm{trans}}}} \right)\) is constant while the solar-thermal heat generation (\({\dot Q_{{\mathrm{gen}}}}\)) depends on the optical concentration. At lower optical concentrations, \(\dot Q_{{\mathrm{gen}}} = \dot m_{{\mathrm{evap}}} \times H_{{\mathrm{LV}}} < \dot m_{{\mathrm{trans}}} \times H_{{\mathrm{LV}}}\) where \(\dot m_{{\mathrm{evap}}}\) is the corresponding rate of water evaporation. At COpt = 1, \({\dot m_{{\mathrm{trans}}}} \gg {\dot m_{{\mathrm{evap}}}}\) leading to heat delocalization due to parasitic losses, which leads to a lower evaporation rate compared with an ideal device. At higher optical concentrations, (COpt ≥ 2), \(\dot Q_{{\mathrm{gen}}}\) increases at a given \(\dot m_{{\mathrm{trans}}}\) and approaches the ideal condition where \(\dot Q_{{\mathrm{gen}}} = \dot m_{{\mathrm{evap}}} \times H_{{\mathrm{LV}}} \approx \dot m_{{\mathrm{trans}}} \times H_{{\mathrm{LV}}}\). A balance in heat generation and water transport is therefore critical in all interfacial evaporation systems. The rate of evaporation at 1 Sun can be improved by tailoring the geometric parameters of the capillaries or its orientation to decrease \(\dot m_{{\mathrm{trans}}}\) to realize optimal water and heat management conditions.
It is worth noting that, in the context of water evaporation, the open-capillary nature of the SWSA sheet provides major advantages. First, the thermal resistance of a water film sustained inside the open capillary tubes of the SWSA sheets is given by \(R_{{\mathrm{film}}}^{{\mathrm{Open}}} = L/(A \times k)\), where k(W/(mK)) is the water thermal conductivity, A is the surface area of the capillary in contact with water and L is the average thickness of the water layer. The small value of L in open capillary tubes means that the temperature difference across the water film is minimal and the temperature at the water–air interface is close to that of the absorber–water interface. As the evaporation enthalpy is inversely proportional to the water temperature, the high temperature at the water–air interface leads to higher evaporation rates (Supplementary Note 15, Supplementary Fig. 19). Furthermore, the evaporation rate of water is also given by \(\dot m_{{\mathrm{water}}} = C_{{\mathrm{evap}}}A\left( {x_{{\mathrm{max}}} - x} \right)\) where Cevap is the evaporation coefficient, A is the area, xmax is the maximum humidity ratio of saturated air and x is the actual humidity ratio in air. The term (xmax − x) represents the concentration driving force that leads to evaporation30. For a closed capillary, the accumulated evaporation leads to an increase in the partial pressure of water vapour. Once the partial pressure is equal to the saturation pressure, P (x = xmax), evaporation becomes limited by the diffusion of water molecules from the closed capillary. The large A and small L of an open-capillary tube architecture overcomes the concentration-gradient problem that is associated with closed-capillary tubes.
Solar-panel properties of the SWSA sheets
Our super-wicking surface, on which water wicks the super-absorber surface spontaneously against gravity, can adopt already existing solar panel designs. Recently, double-sided solar panels were introduced as a solution to increase the efficiency of photovoltaic panels by absorbing scattered light, showing a ~50% increase in electric-power generation while reducing area-related costs31. Figure 4a shows the measured evaporation rate under COpt = 1 for single-sided versus double-sided SWSA sheets (Extended Data Fig. 6) mounted in the vertical plane. The double-sided SWSA evaporation rate is \(\dot m^{{\mathrm{Double}}}\) ≈ 1.26 kg m−2 h−1, whereas the single-sided SWSA evaporation rate is \(\dot m^{{\mathrm{Single}}}\) ≈ 0.5 kg m−2 h−1, showing ≈150% increase in the mass evaporation rate in the double-sided sheets compared with the single-sided sheets (Supplementary Note 16 and Supplementary Fig. 20). Note that the evaporation rates reported here are for a vertically mounted SWSA sheet, which changes the water transport properties and the overall evaporation rate compared with horizontally mounted SWSA sheets (Fig. 3e,f). Explosive steam generation from the double-sided SWSA surface at COpt = 2 is shown in Supplementary Video 3.
a, Mass loss of water over time for single-sided and double-sided SWSA sheets for COpt = 1. The double-sided SWSA sheets benefit from scattered light and demonstrate larger evaporation rates. b, Mass loss of water over time for COpt = 1 as a function of incidence angle. c, Outdoor measurement of water mass evaporation for a flat SWSA and an SWSA sheet tilted to maximize the incident solar flux over the course of 8 h on 30 June 2018 at Rochester, NY, United States. A photograph of the devices is shown in the inset. d, The corresponding solar irradiance over the same period.
Furthermore, the solar-panel geometry of the SWSA sheet enables the orientation angle of the device to be adjusted to maximize the incident solar flux at its surface. The average solar irradiance available at Earth’s surface varies throughout the year due to variation in the solar zenith angle and radial distance of Earth’s surface from the Sun. By adjusting the orientation angle of the solar panel, available solar flux can be increased by up to ∼1.5–1.7× over the flat surface. Even at some high-latitude geographical locations, such as Rochester, NY, United States (latitude, 43.1167° N; longitude, 77.6767° W), vertically mounted surfaces receive larger solar irradiance from the months of October to February over a flat surface (Extended Data Fig. 7). Figure 4b shows the change in water mass due to evaporation over time at COpt = 1 for different angles of light incidence. Clearly, the water-evaporation rate decreases with increasing the incidence angle, that is, with decreasing the solar flux. Note that the dark-condition water-evaporation rate changes as a function of the incidence angle, Θ, as the water transport properties and the effective surface area at the water–air interface have orientation-angle dependence (Supplementary Fig. 20). Moreover, the ability to control the evaporation rate by controlling the contact and relative angle of SWSA means that it can operate as an intelligent evaporation system that could function when needed as well as automatically tune the evaporation rate5. We conducted an outdoor measurement of mass-loss rate with two SWSA devices; a flat SWSA device and a tilted SWSA device (Fig. 4c, inset) with a tilt angle of 25° from horizontal to maximize the flux incident from the Sun on 30 June 2018 at Rochester, NY, United States, (solar zenith angle, ≈25°), that is, the tilted SWSA surface was normal to the incident solar radiation (Extended Data Fig. 8). Figure 4c shows the evaporated mass over the course of 8 h, demonstrating a ~3% increase in the water-evaporation rate for the tilted sample compared with the flat sample. The corresponding solar irradiance available at the flat surface is shown in Fig. 4d. Note that the difference in the average solar irradiance that is available at flat and tilted surfaces of the same area is minimum in the month of June at Rochester, NY (Extended Data Fig. 7d) leading to the small difference in water-evaporation rates between the two panels. The corresponding solar irradiance available at a flat surface is shown in Fig. 4d. Outdoor measurements for the next three consecutive days (1 July 2018–3 July 2018) of the same tilted device are shown in Extended Data Fig. 9 along with absorber surface temperature and corresponding solar irradiance. Similar to a photovoltaic (PV) solar panel, our SWSA panel can be mounted at a fixed angle over a given season and the angle of tilt can be manually changed from season to season to optimize incident solar flux. This strategy would both minimize the complexity that is associated with a live solar-tracking system and sanitize more water.
Water sanitation using the SWSA sheet
Figure 5a shows a schematic of the solar sanitation setup for water purification (see Methods; Supplementary Fig. 21). We demonstrated water sanitation for 14 of the most common types of contaminants, including various heavy metals (Fig. 5b), light metals (salts; Fig. 5c), and industrial, domestic and agricultural pollutants (Fig. 5d, Supplementary Figs. 21–25, Supplementary Table 1). A water sample collected from a nearby pond was also solar purified using the same SWSA surface and the density of bacteria in the contaminated and purified water samples was measured32 (Supplementary Fig. 25). The contamination level was reduced by 4–5 orders of magnitude for all contaminants and was well below the WHO standard for safe drinking water. Photographs of the Cr(ii)-contaminated and rhodamine 6G (R6G)-dye-contaminated and solar-purified water samples are shown in Fig. 5e. All of the sanitation experiments were performed using the same SWSA sheet. The reusability of the device for a wide spectrum of contaminants is important for practical applications, particularly in secluded and poor communities. Owing to the open-capillary architecture of SWSA surface, the contaminants that remain on the SWSA surface after several cycles of operation (Fig. 5f, top) can easily be cleaned by applying pressurized water (Fig. 5f, bottom; Extended Data Fig. 10) to its surface, which substantially reduces the maintenance cost for commercial and personal solar-based water sanitation systems (Supplementary Video 4).
a, A schematic of the water sanitation/desalination setup. b–d, Water sanitation of various heavy metals (b), salts (c) and industrial (dye, ethylene glycol (EG) and glycerin), domestic (glycerin and detergent) and human/animal excretory product/agricultural pollutants (urea/simulated urine) (d). e, Images from before (left) and after (right) water that was sanitized for Cr(ii) (top) and R6G dye (bottom). f, SWSA sheets after desalination show dry salt on the open capillaries (top), which can be easily removed (bottom).
Discussion and outlook
The demonstrated device has the potential to be used as part of the solution to the global water crisis due to its simplicity, durability, reusability, efficiency and compatibility with solar-thermal technology. While Al is cheap and abundant, other materials can be treated to become SWSA using femtosecond laser processing19. For example, Al electrodes at the back of silicon PV cells can be treated to become SWSA, which can increase the PV efficiency by cooling it, while simultaneously generating clean water19,33. Further investigations to realize large-scale SWSA sheets are essential for generating sufficient amounts of clean water for personal use and for commercial applications. Moreover, Al sheets can be laser treated to fabricate selective solar-absorber super-wicking surfaces to reduce radiation losses to further increase efficiency of the device at a given optical concentration34. Finally, sheets can be integrated with the already existing solar-panel tracking systems to increase their efficiencies. In fact, systems that assume high evaporation efficiencies using optical concentration are unrealistic unless they can be integrated with a solar tracking system such that the Sun radiation lies within the acceptance angle of the concentrating lenses. Although we used optical concentration to increase the device efficiency, the solar-panel architecture of the device allows for thermal concentration as well35.
Methods
Femtosecond laser fabrication of SWSA surfaces
A description of the experimental setup for fabricating the SWSA surface is provided in Supplementary Fig. 1a. In particular, a sheet of Al foil of 200 µm thickness and 22 mm × 40 mm dimensions, mounted on an xy translational stage, was scanned normal to the femtosecond laser beam (Ti: Sapphire, Spittfire, Spectra Physics) operating at a wavelength of 800 nm, 780 µJ per pulse energy and 1 kHz repletion rate. In a typical experimental procedure, the laser beam was focused onto the target surface with a focal spot size of ∼100 µm using a planoconvex lens with a focal length of 250 mm and scanned in a spiral manner. The scan speed was optimized for 0.5 mm s−1 and interline spacing was 100 µm to generate an SWSA surface with maximum optical absorbance.
Optical absorbance measurements in the ultraviolet–visible–near-inrared and mid-infrared regions
The hemispherical optical reflectance of the SWSA surface was measured in the spectral range of 0.25–2.5 µm using a PerkinElmer Lambda-900 double-beam spectrophotometer coupled with a 50-mm-diameter integrating sphere. Similarly, hemispherical reflectance in the mid-infrared region (2.5–25 µm) was measured using a Thermo Fisher Scientific Nicolet 6700 FTIR spectrometer coupled with a PIKE research integrating sphere. An accessory (B0137314) was used with the PerkinElmer 900 spectrophotometer to measure specular reflectance in the spectral range of 0.25–2.5 µm for incident angles ranging from 15° to 75° to demonstrate omnidirectional or Lambertian absorptive surfaces. In a similar manner, an accessory (PIKE VeeMAX III) coupled with the Thermo Scientific Nicolet 6700 FTIR spectrometer was used to measure specular reflection in the spectral range of 2.5–25 µm for incident angles ranging from 30° to 80°. As the SWSA sample is opaque, hemispherical/specular absorbance is complimentary to measured scattering/reflectance in ultraviolet–visible–near-infrared and mid-IR range; therefore, absorbance is obtained using A = 1 − R.
Surface topography and surface morphology measurements
The surface topography and depth profile of hierarchical microstructures on the surface of the SWSA sheets was measured using a 3D scanning laser microscope (Keyence VK 9710-K) with an elevation resolution of 0.2 µm. The surface morphology of the SWSA surface was measured using a SEM/FIB Zeiss-Auriga scanning electron microscope.
Wetting dynamics measurements
Two types of water-wetting-dynamics measurements were performed. In the first measurement, the SWSA sample was mounted onto a vertical platform (Supplementary Fig. 6) and 200 µl water was placed at the lower end of the SWSA sample. The video of water-wetting dynamics was recorded with a high-speed camera at 200 frames per s (Supplementary Videos 1 and 2). The video, shown in Supplementary Videos 1 and 2, speed was slowed down by 10× with video processing software and snapshots were captured at different moments to generate Fig. 2d and Extended Data Fig. 2a. In another set of measurements, the SWSA sample was mounted on a micrometre-control translational stage with motion in the vertical direction (Supplementary Fig. 7a). The lower end of the SWSA surface was allowed to touch the water surface placed on the computerized weighing balance. When the lower end of the SWSA surface touched the water surface, a sudden decrease in the mass of water was observed. The decrease in the water mass gives the water-wetting rate on a vertically mounted SWSA surface and, ultimately, the rate of water-mass uplifting.
Calibrating the solar simulator and power meter and designing the sample plane
The solar simulator (Sanyu) with an AM1.5G airmass filter was first calibrated for 1 Sun (1,000 W m−2) using a NREL-certified PV reference solar cell (PV Measurements). An output of a thermopile power meter (FieldMax II TO, Coherent), set at a wavelength of 500 nm, corresponding to 1,000 W m−2 from the calibrated solar simulator was used as a unit of 1 optical concentration. For example, thermopile power meter results for 283 mw for 1,000 W m−2 of incident flux from the solar simulator. The head of the pyroelectric power meter was circular in shape with a diameter of 19 mm (area, 2.83 cm2). A planoconvex lens (focal length, 300 mm; diameter, 150 mm) was mounted at the output port of the solar simulator to concentrate a 10 cm × 10 cm square beam of the solar simulator into a 4 cm × 4 cm square beam in the horizontal plane. The most uniform area of 2.5 cm × 2.5 cm (the sample size that was exposed with light is 2.0 cm × 2.0 cm) at the centre of the 4 cm × 4 cm beam was used for the measurement. To vary the optical concentration in the xy plane, we varied the current in the xenon lamp and waited for 20–30 min every time the current was changed for the solar simulator to stabilize before measurement. A time of 5–10 min was given to the thermopile head to obtain stabilized readings. For a given current passing through the xenon lamp, power was measured at the 2.5 cm × 2.5 cm central region of the 4 cm × 4 cm beam with an average time of 20 s. The detector was then moved 6 mm in the x direction to measure the time-averaged power at the next spot. Using this method, we measured the power at four locations in the xy plane (Supplementary Fig. 17) to estimate the error in the optical concentration (Fig. 3e). The current in the solar simulator was varied to adjust solar irradiance from 1,000 W m−2 (283 mW at thermopile head) to 5,000 W m−2 (1,415 mW). The solar simulator was turned on for 20–30 min to obtain a stabilized output, and times of 5–10 min were given to the thermopile head to obtain stabilized readings.
Temperature measurement of the SWSA surface
The SWSA sample was mounted onto the surface of polystyrene foam in the horizontal plane. Two thermocouples (TC1 and TC2) were mounted onto the front and back surface of the SWSA sheet or unprocessed Al sheet (Supplementary Fig. 17). The surface of the SWSA samples was irradiated with light from a vertically downward beam of the solar simulator. The outputs of the thermocouple were fed to the computer through an electronic data logger (TC08, Omega Engineering) and stored in the computer for further processing. The temperatures of the front and back surfaces of the SWSA and unprocessed Al sheets were measured for different optical concentrations (Extended Data Fig. 3).
Indoor water-evaporation measurements in the vertical and horizontal planes
Water-evaporation measurement in the horizontal plane
The SWSA sample of 20 mm × 36 mm was bent into a U shape to generate a square 20 mm × 20 mm horizontal light absorber and evaporator surface (working area) and two parallel surfaces, each of 8 mm × 20 mm, (auxiliary surfaces) to transport water on the absorber surface. The U-shaped sample was mounted onto a low-cost polystyrene thermal insulating foam (which is generally used in packaging; thickness, 7 mm), and cut into a circular shape to fit into the opening of a glass or plastic water container (Extended Data Fig. 4). The diameter of the insulating foam that was used for mounting was adjusted in such a way that it floated on the water surface. The water container along with the U-shaped SWSA sample mounted onto the insulating foam was placed onto a computerized electronic weighing balance (Radwag SMB-60/AS 60/220.R2) to measure the mass of the water with time with a sampling rate of 1 data point per second. A square aperture of 20 mm × 20 mm, which was cut into a piece of black thick cardboard and which was carefully aligned with the absorber surface, was used to prevent additional light falling onto the non-sample area to avoid additional solar-thermal heating (Extended Data Fig. 4e–g). First, the water vaporization mass in the dark, with and without the SWSA surface, under the same opening was measured for 1 h as a reference for self-evaporation. Later, the loss in water mass, with and without the SWSA surface, was recorded for different optical concentrations (COpt = 1–5). Water was changed after each measurement to delete any thermal storage history in the water.
Two K-type thermocouples, of which the first was mounted onto the SWSA surface and the second was installed just below the insulating foam, were used to measure the absorber surface and water temperature using an electronic data logger (TC08, Omega Engineering). Thermal images of the absorber surface and bulk water were recorded using an infrared camera (FLIR TG167; Extended Data Fig. 4h–k).
Water-evaporation measurements in the vertical plane
The SWSA sample (area, 20 mm × 28 mm) was used for water-evaporation measurements in the vertical plane. In this case, the surface area of 20 mm × 20 mm was used as a solar-thermal vapour generator (working area), while the remaining 8 mm × 20 mm area was used as an auxiliary surface to transport water to the absorber surface. The SWSA sample, which was vertically mounted onto the surface of polystyrene foam (Supplementary Fig. 20, Extended Data Fig. 4), was floated on the water surface. The complete system was placed onto a computerized balance to measure the loss in water mass for a different angle of mounting. The SWSA sample plane was bent at different angles (0°, 30°, 45° and 60°) from vertical to measure effects of angle of light incidence (light flux) on the evaporation rate. We first measured the dark-condition water-evaporation rate for each angle for 50 min, and then irradiated the absorber surface with COpt = 1 Sun to measure the loss in water mass under solar irradiation. The dark-condition evaporation rate was subtracted from the corresponding evaporation rate under light illumination. The average evaporation rate was measured by linear fitting of five different segments of 10 min.
Outdoor water-evaporation measurements
Two SWSA samples, each with an area of 20 mm × 30 mm, were bent at a height of 10 mm to obtain a 20 mm × 20 mm working area and a 10 mm × 20 mm auxiliary area for the water transport. The first sample was bent at a right angle to generate a flat absorber, whereas the second sample was bent at 65° from vertical to generate an absorber plane to directly face the Sun at a zenith angle of 25°. Both of these SWSA samples were installed onto the surface of polystyrene foam and allowed to float on the surface of the water. To compare the rate of water evaporation from flat and tilted samples (30 June 2018), the mass of water in each container was measured at intervals of 30 min for 8 h. For the next three consecutive days (1 July 2018–3 July 2018), the water container with the Sun-faced sample was placed onto a computerized balance to measure the water loss for 10 h, 12 h and 7 h (Extended Data Fig. 9) on 1 July, 2 July and 3 July, respectively. The temperature of the absorber surface was measured using a thermocouple and the corresponding solar irradiance was measured using a Apogee 420 pyranometer.
Solar-based water sanitation and water quality testing
Preparation of contaminated water
Contaminated water samples were prepared by dissolving a known amount of impurities into double-distilled water. To simulate 500 ppm of heavy-metal-contaminated water (Cd, Cr, Pb, Ni), 20 mg salt (Cd(NO3)2, Cr2O3, PbCl2 or NiCl2) of the corresponding heavy metal was dissolved into 40 ml of double-distilled water. Similarly, standard salt solutions of 104 ppm (saline water) were simulated by dissolving 400 mg of corresponding salts (NaCl, KCl, MgSO4 and CaCl2) into 40 ml of double-distilled water. Ethylene glycol and dyes are industrial pollutants used as coolants and colouring, respectively. A 10 ml solution (11.1 g) of ethylene glycol was ultrasonically dissolved into 40 ml of distilled water to prepare 2.77 × 105 ppm aqueous solution of ethylene glycol. Similarly, 4.33 mg of R6G dye was dissolved into 40 ml of double-distilled water to obtain a 108.25 ppm dye solution. Detergent and glycerin are two common domestic pollutants. Sodium dodecyl sulfate (SDS; C12H25SO4Na) is a surfactant that is generally used in detergents, dishwashing liquids, toothpaste and all types of soaps. The 10 mM solution of SDS was prepared by dissolving 144.186 mg of SDS in 50 ml of double-distilled water, which is the equivalent of 2.88 × 103 ppm detergent solution. Urea is an agricultural pollutant and the main component of human and animal excretory product. A urea solution of 800 ppm was prepared by dissolving 32 mg of urea (NH2CONH2) into 40 ml of double-distilled water.
Solar-based water-sanitation setup
The SWSA device, which consisted of the SWSA sample mounted onto polystyrene foam, floated on the water surface with the absorber surface in the horizontal plane. The water-wet absorber surface of the device was irradiated with normally incident light from a spectrally calibrated solar simulator to generate vapour. The water vapour condensates at the walls of a transparent and cleaned container were collected as pure water. In detail, the SWSA sample bent into a U shape with a working area of 30 mm × 30 mm and two parallel water transport surfaces of 30 mm × 8 mm was mounted onto the surface of polystyrene insulating foam (similar to that shown in Supplementary Fig. 21a,c). The system could float on the surface of contaminated water in a glass container (first container). The first container, with contaminated water and the absorber, was placed into another precleaned glass container (second container) with a transparent glass lid with ∼95% optical transparency. The outer surface of the first container and the inner surface of the second container was cleaned several times with double-distilled water to avoid pre-existing contaminants in the region between two containers in which pure water was collected. The complete system (Supplementary Fig. 21c) was placed below the solar simulator with COpt = 2. Water evaporated, condensed on the top and interior walls of the second container and collected in the region between two containers. Each contaminated water sample was evaporated for 2 h to obtain about 5–7 ml of purified water.
Water testing
Pure water samples, which were obtained from the solar sanitation of simulated contaminated water such as heavy metals and light metals (salts), were tested by Culligan Water—a NELAP-accredited water testing laboratory—using inductively coupled plasma mass spectroscopy. EPA standard method 200.8 R5.4 was used to measure the concentrations of heavy metal in the purified water, whereas EPA 200.7 R4.4 was used to measure the concentrations of Ca, Mg, K and Na.
Ultraviolet–visible optical absorption spectroscopy was used to measure the concentration of dye and urea in purified water using Beer–Lambert law. The standard solutions were first prepared by dissolving a known amount of solvents followed by its dilution. For example, 13.5 ppm to 0.005 ppm solutions of R6G were prepared to draw a calibration line. The concentration of dye/urea in the purified water was measured on the basis of the absorbance value at a given wavelength (Supplementary Fig. 24).
The concentration of ethylene glycol, glycerol and detergent in purified water was measured using a physical method of contact-angle measurements36. The standard solutions of each impurity in double-distilled water were prepared to draw a line of calibration. The contact angle for each of the standard solutions was measured by putting 200 µm droplets on a superhydrophobic surface. A calibration curve (contact angle versus concentration) was drawn for each impurity to obtain a concentration of impurity in the purified water.
A sample of dirty water, collected from a nearby pond, was solar sanitized using the SWSA surface (Supplementary Fig. 25a,b for dirty water and purified water, respectively). The water samples before and after solar sanitation were tested for the presence of bacteria using the commercially available Bacteria in Water Test Kit (PRO-LAB, BA110). The water sample (1 ml) from dirty or sanitized water sample was mixed thoroughly with the bacterial growth medium provided in the kit. The bacterial growth medium with the dirty or purified water sample was transferred separately into different sterilized Petri dishes and left for 48 h for bacterial growth. The bacterial density from solar-sanitized dirty water and the control sample was calculated using the colony-counting method32. The Petri dish corresponding to dirty water sample had more than 500 colonies (Supplementary Fig. 25c), whereas no colony was visible in the other Petri dish (Supplementary Fig. 25d) in which sanitized water was used.
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
References
Florke, M. et al. Water competition between cities and agriculture driven by climate change and urban growth. Nat. Sustain. 1, 51–58 (2018).
Porse, E. et al. The economic value of local water supplies in Los Angles. Nat. Sustain. 1, 289–297 (2018).
Ni, G. et al. Volumetric solar heating of nanofluids for direct vapor generation. Nano Energy 17, 290–301 (2015).
Bae, K. et al. Flexible thin-film black gold membranes with ultrabroadband plasmonic nanofocusing for efficient solar vapour generation. Nat. Commun. 6, 10103 (2015).
Tao, P. et al. Solar-driven interfacial evaporation. Nat. Energy 3, 1031–1041 (2018).
Ghasemi, H. et al. Solar steam generation by heat localization. Nat. Commun. 5, 4449 (2014).
Yu, S. et al. The impact of surface chemistry on the performance of localized solar-driven evaporation system. Sci. Rep. 5, 13600 (2015).
Li, X. et al. Graphene oxide-based efficient and scalable solar desalination under one Sun with a confined 2D water path. Proc. Natl Acad. Sci. USA 113, 13953–13958 (2016).
Ni, G. et al. Steam generation under one Sun enabled by a floating structure with thermal concentration. Nat. Energy 1, 16126 (2016).
Jackson, R. D. & Van Bavel, C. H. M. Solar distillation of water from woil and plant materials: a simple desert survival technique. Science 149, 1377–1379 (1965).
Xu, W. et al. Flexible and salt resistant Janus absorbers by electrospinning for stable and efficient solar desalination. Adv. Energy Mater. 8, 1702884 (2018).
Ni, G. et al. A salt-rejecting floating solar still for low-cost desalination. Energy Environ. Sci. 11, 1510–1519 (2018).
Sutton, S. Preliminary Desk Study of Potential for Self Supply in Sub-Saharan Africa (RWSN/WaterAid, 2004).
Liu, Y. et al. A bioinspired, reusable, paper-based system for high-performance large-scale evaporation. Adv. Mater. 27, 2768–2774 (2015).
Hu, X. et al. Tailoring graphene oxide-based aerogels for efficient solar steam generation under one Sun. Adv. Mater. 29, 1604031 (2017).
Wang, X., He, Y., Liu, X., Cheng, G. & Zhu, J. Solar steam generation through bio-inspired interface heating of broadband-absorbing plasmonic membranes. Appl. Energy 195, 414–425 (2017).
Vorobyev, A. Y. & Guo, C. Colorizing metals with femtosecond laser pulses. Appl. Phys. Lett. 92, 041914 (2008).
Vorobyev, A. Y. & Guo, C. Metal pumps liquid uphill. Appl. Phys. Lett. 94, 224102 (2009).
Vorobyev, A. Y. & Guo, C. Laser turns silicon superwicking. Opt. Express 18, 6455–6460 (2010).
Vorobyev, A. Y. & Guo, C. Making human enamel and dentin surfaces superwetting for enhanced adhesion. Appl. Phys. Lett. 99, 193703 (2011).
Vorobyev, A. Y., Makin, V. S. & Guo, C. Brighter light sources from black metal: significant increase in emission efficiency of incandescent light sources. Phys. Rev. Lett. 102, 234301 (2009).
ElKabbash, M. et al. Tunable black gold: controlling the near-field coupling of immobilized Au nanoparticles embedded in mesoporous silica capsules. Adv. Opt. Mater. 5, 1700617 (2017).
Zhou, L. et al. 3D self-assembly of aluminium nanoparticles for plasmon-enhanced solar desalination. Nat. Photon. 10, 393–398 (2016).
Rye, R. R., Mann, J. A. & Yost, F. G. The flow of liquids in surface grooves. Langmuir 12, 555–565 (1996).
Washburn, E. W. The dynamics of capillary flow. Phys. Rev. 17, 273–283 (1921).
Drelich, J., Chibowski, E., Meng, D. D. & Terpilowski, K. Hydrophilic and superhydrophilic surfaces and materials. Soft Matter 7, 9804–9828 (2011).
Zhao, F. et al. Highly efficient solar vapour generation via hierarchically nanostructured gels. Nat. Nanotechnol. 13, 489–495 (2018).
Miyazaki, M. et al. Infrared spectroscopic evidence for protonated water clusters forming nanoscale cages. Science 304, 1129–1137 (2004).
Fujii, A. & Kenta, M. Infrared spectroscopic studies on hydrogen-bonded water networks in gas phase clusters. Int. Rev. Phys. Chem. 32, 266–307 (2013).
Engel, Y. A. Heat And Mass Transfer: Fundamentals And Applications 3rd edn (McGraw-Hill, 2006).
Guerrero-Lemus, R., Vega, R., Kim, T., Kimm, A. & Shephard, L. E. Bifacial solar photovoltaics—a technology review. Renew. Sustain. Energy Rev. 60, 1533–1549 (2016).
Bhardwaj, A. K. et al. Power and time dependent microwave assisted fabrication of silver nanoparticles decorated cotton (SNDC) fibers for bacterial decontamination. Front. Microbiol. 8, 330 (2017).
Wang, Wenbin et al. Simultaneous production of fresh water and electricity via multistage solar photovoltaic membrane distillation. Nat. Commun. 10, 3012 (2019).
Jalil, S. A. et al. Spectral absorption control of femtosecond laser-treated metals and application in solar-thermal devices. Light Sci. Appl. 9, 14 (2020).
Kraemer, D. et al. High-performance flat-panel solar thermoelectric generators with high thermal concentration. Nat. Mater. 10, 532–538 (2011).
Kaufmann, T. C., Engel, A. & Rémigy, H.-W. A novel method for detergent concentration determination. Biophys. J. 90, 310–317 (2006).
Acknowledgements
We thank M. Mann for his assistance in recording high-quality videos. We acknowledge financial support from the Bill & Melinda Gates Foundation (OPP1157723), the National Science Foundation: Partnership for Innovation grant (no. 1701163), and the US Army Research Office (W911NF-15–1–0319).
Author information
Authors and Affiliations
Contributions
S.C.S. and C.G. discussed and defined the project. S.C.S. initiated and led the project in experimental design, sample fabrication and procurement, and performed most of the measurements. Z.L. and X.L. participated in the wicking-dynamics and water-evaporation measurements. B.R. and M.M. participated in the outdoor water-evaporation measurements and graphical design. S.A.J. performed air–water surface area measurements. Z.Z. and J.Z. participated in project discussions. S.C.S. coordinated all measurements, organized manuscript figures and technical content. M.E. assisted in figure organization and technical content. S.C.S., M.E. and C.G. discussed results and interpretation, prepared and finalized the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Optical absorption of SWSA sheets.
a, Hemispherical optical absorbance of two SWSA sheets (Black metal shallow grooves (BMSG; Magenta) and black metal deep grooves (BMDG; red) with absorbance of a polished Al sheet as a reference in UV-visible-NIR. b, Hemispherical absorbance of BMSG-SWSA sheets in mid-IR region with absorbance of a polished Al sheet as a reference. Specular optical absorbance of BMSG-SWSA surface for different incident angles in c, visible-NIR and d, mid-IR spectral regions. Inset of (c) shows schematic of solar zenith angle with flat floating surface. The persistence of strong absorption at a wide range of angles, that is, omnidirectional absorption, is an important advantage of our SWSA system.
Extended Data Fig. 2 Water-wicking dynamics of SWSA sheet.
a, Time-snapshots of water wetting (up-hilling) dynamics on the SWSA surface (see also Supplementary Vidoes 1 and 2). b, The position of water wet-front (left black line) and corresponding velocity with time (vWF = dWWF/dt) (right blue line) graphs for water wet-front. c, Variation in the velocity of water-wet-front with distance on the vertically mounted SWSA surface.
Extended Data Fig. 3 Indoor water evaporation measurements from horizontally mounted SWSA sheet.
a, An SWSA sheet turned into “U” shape with 20 mm×20 mm surface for soalr-absorption and water-evaporation. The “U” shaped SWSA sheet mounted on a polystyrene foam b, top view and c, bottom view. d, An assembly of SWSA surface/ polystyrene foam floating on the dirty water surface. A similar set-up in a smaller water container covered with a black cardboard with an aperture of 20 mm × 20 mm for e, dark measurement and f, under solar simulator (top view) and g, a side view showing foam. Thermal imaging of temperature on h, SWSA surface, i, of foam j, water just below the foam and k, bulk water after 30 minutes of turning on the solar simulator at Copt = 3.
Extended Data Fig. 4 Demonstration of heat localization on the SWSA susrafce shown in Extended Data Fig. 3.
Temperatures of the SWSA surface and bulk water just below the insulating foam, in Extended Data Fig. 4, over time at 1 sun and 3 sun optical concentration. The high-temperature difference between the SWSA sheet and water indicates heat localization at the SWSA surface. This is enabled through the thermally insulating foam that limits heat conduction to water as well as the minimal contact required by the SWSA surface and water.
Extended Data Fig. 5 Solar-thermal heating of SWSA and polished Al sheets.
a, The schematic for the temperature measurement of the front and back surfaces of SWSA and polished Al surface under different optical concentrations. The SWSA sample was placed at thermally insulating foam. TC1 and TC2 are thermocouples recording temperature through an electronic data logger (TC 08 Omega engineering), where TC2 was mounted through a small hole made on the insulating foam. Temperature rise at the front and back surfaces of b, unprocessed Al and c, SWSA surface under different optical concentrations. d, Variation in the dT/dx scattered data and corresponding linear fit for SWSA and unpolished Al samples with incident optical flux. The average response time of the SWSA sheet τ90, that is, the time it takes for the sheet to reach 90% of its maximum temperature, is ~ 81 ±7 s, and the relaxation time τ10, that is, the time it takes for the temperature to drop to 10% of its maximum value, is 103±6 s.
Extended Data Fig. 6 Enhanced evaporation from double sided SWSA sheet.
Double-sided SWSA mounted vertically a,b, front view, and c, back view under Copt = 1 Sun, and d, back view under Copt = 2 Sun showing steam generation, e, water evaporation with time for one-sided and double-sided SWSA along with corresponding dark evaporation. A white plan paper is vertically mounted at the back side to scatter/reflect light.
Extended Data Fig. 7 Annual variation in the average solar irradiance at three geographical locations of United States.
Monthly variation of a, cosθ, where θ is zenith angle for sun. Available average solar flux on b, flat surface in the horizontal plane (inset schematic of orientation of absorber surface relative to the sun), and c, on the solar trackable SWSA surface, d, Monthly variation of average solar irradiance on flat surface in horizontal plane, in vertical plane and at the surface directly facing to the sun at Rochester, NY, USA (Latitude: 43.1167; Longitude:-77.6767). We calculated average available solar irradiance at the flat surface using online resource (www.solarelectricityhandbook.com) (b) and then divide average solar irradiance available at flat surface with corresponding cos θ values (shown in a) to get values for direct sun facing panel (c).
Extended Data Fig. 8 Outdoor water evaporation measurements from flat-lying and sun-faced SWSA sheets.
a, Photographs of two 30 mm × 20 mm SWSA samples. The first sample was bent at right angle to make flat mounted SWSA device while the second SWSA sample was bent at 65 degree from vertical to directly face the Sun at zenith angle 25° in July Month at Rochester, NY, USA (Latitude: 43.1167; Longitude:-77.6767). Both the samples were bent at the height of 10 mm to make 20 mm × 20 mm surface area available for solar-absorption and water evaporation. b, Both samples were mounted at polystyrene foams. The surface of polystyrene foam was flat to fabricate flat system, while the surface of a thick polystyrene foam was slanted at 25 degrees from vertical to support tilted SWSA sheet. Both of the SWSA samples along with polystyrene foam was fixed on the surface of water in two similar containers. Water containers were wrapped with thick-white adhesive tapes to avoid direct heating of water from ambient heat or Sunlight. Apogee smart USB pyranometer, SP-420, was used to measure solar irradiance throughout the experiment. c, Experimental arrangement for water evaporation measurements. Containers with flat and tilted SWSA samples were placed on two electronic balances connected with computer to measure mass of the water remained in the container with time. d, The flat SWSA sample on the balance e,f, SWSA sample mounted at 25° from vertical to directly face the Sun (e) Front view, and (f) side views of sun-faced SWSA sample. Small holes were cut on adhesive tapes, wrapped on glass container, as viewing ports to see water level.
Extended Data Fig. 9 Outdoor water evaporation measurements from the Sun-faced SWSA sheet.
Outdoor water evaporation measurements (Top panels; black curves) from the SWSA sample mounted at 65° from vertical (solar zenith angle is 25 degree) on three consecutive days starting from July 1st, 2018 to July 3rd, 2018 under a, partially cloudy b, heavily cloudy and c, sunny days with corresponding temperatures of absorber surface (Top panels; blue curves) and solar irradiances (Bottom panel; red curves) available. It is important to notice that intermittent drop in solar irradiance due to cloud has little or no effect on the absorber temperatures and water evaporation. The same SWSA sample was continuously used for more than thirty hours.
Extended Data Fig. 10 Open capillary architecture facilitation in the salt cleaning.
Accumulation of salt on the SWSA surface after two hours of evaporation of concentrated (104 mg/liter) salt solution in the horizontal plane (Extended Data Fig. 4). The SWSA surface can transport and evaporate water until entire surface get covered with thick layer of salt. c, The accumulated salt can be easily removed from SWSA surface by flushing water for reusability of absorber and cheap maintenance of solar sanitation device, d, The SWSA, surface after contaminant removal, ready to reuse. (see Supplementary Video 3).
Supplementary information
Supplementary Information
Supplementary Figs. 1–25, Table 1 and Notes 1–21, and captions for Supplementary Videos 1–4.
Supplementary Video 1
Water upfilling dynamics on a vertically mounted SWSA sheet in a close view (sample height, 12 mm). The video was slowed by 10× for better measurement and to obtain a larger number of data points.
Supplementary Video 2
Water upfilling dynamics on the same vertically mounted SWSA sheet in full view (sample height, 36 mm). The video was slowed by 10× for better measurement and to obtain a larger number of data points.
Supplementary Video 3
Steam generation from a vertically mounted double-sided SWSA sheet under COpt = 2.
Supplementary Video 4
Video demonstration of the easy cleanability of the SWSA sheet.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Singh, S.C., ElKabbash, M., Li, Z. et al. Solar-trackable super-wicking black metal panel for photothermal water sanitation. Nat Sustain 3, 938–946 (2020). https://doi.org/10.1038/s41893-020-0566-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41893-020-0566-x
This article is cited by
-
High-efficiency bio-inspired hybrid multi-generation photovoltaic leaf
Nature Communications (2023)
-
Biomimetic surface engineering for sustainable water harvesting systems
Nature Water (2023)
-
Rough capillary rise
Communications Physics (2023)
-
Solar steam-driven membrane filtration for high flux water purification
Nature Water (2023)
-
Optimization of bamboo-based photothermal interfacial solar evaporator for enhancing water purification
Environmental Science and Pollution Research (2023)