Abstract
The discovery of two-dimensional (2D) van der Waals (vdW) materials often provides interesting playgrounds to explore novel phenomena. One of the missing components in 2D vdW materials is the intrinsic heavy-fermion systems, which can provide an additional degree of freedom to study quantum critical point (QCP), unconventional superconductivity, and emergent phenomena in vdW heterostructures. Here, we investigate 2D vdW heavy-fermion candidates through the database of experimentally known compounds based on dynamical mean-field theory calculation combined with density functional theory (DFT+DMFT). We have found that the Kondo resonance state of CeSiI does not change upon exfoliation and can be easily controlled by strain and surface doping. Our result indicates that CeSiI is an ideal 2D vdW heavy-fermion material and the quantum critical point can be identified by external perturbations.
Similar content being viewed by others
Introduction
In recent years, there has been a significant interest in 2D vdW materials due to the realization of magnetism in the 2D limit. Over just the past 5 years, various 2D vdW magnetic materials, such as CrI31, Cr2Ge2Te62, VSe23, MnSe24, and FexGeTe2 (x = 3–5)5,6 have been reported. These materials contain 3d magnetic elements in their 2D atomically thin crystals and thus exhibit intrinsic magnetic properties. Compared to bulk 3D materials, the 2D vdW magnetic materials provide additional controllability via strain, surface doping, gating, Moiré potential, etc. Therefore, the discovery of 2D vdW magnetic materials has provided an interesting route to explore new physical phenomena and design novel devices. The realization of magnetic 2D vdW materials is reminiscent of the possible existence of the heavy-fermion state in 2D materials.
The heavy-fermion materials containing rare-earth or actinide ions can be regarded as prototypes of lattice Kondo systems, where the interplay between the Ruderman–Kittel–Kasuya–Yoshida (RKKY) interaction and the Kondo effect determines the ground state. When the RKKY interaction dominates, local moments tend to form long-range magnetic order at low temperatures, usually the antiferromagnetic (AFM) phase. On the other hand, when the Kondo effect prevails, local magnetic moments are screened by itinerant conduction electrons leading to the paramagnetic (PM) Kondo resonance state (strong hybridization between f electrons and conduction electrons; f−c hybridization). Due to the small energy scales of two competing interactions, the ground state can be easily tuned through a quantum phase transition by external perturbations, such as pressure, chemical doping, or magnetic field7,8,9,10,11,12,13,14,15,16,17. In the vicinity of QCP, anomalous phenomena often occur including unconventional superconductivity and non-Fermi liquid. If a heavy-fermion state can be realized in 2D vdW materials, it can provide a new platform to study QCP, magnetism, and superconductivity with additional controllability.
There have been several attempts to realize the heavy-fermion state in the 2D limit. The dimensionality tuning from 3D to 2D heavy-fermion state was firstly reported by using the epitaxially grown CeIn3/LaIn3 superlattice18. Several other artificial Kondo superlattices have been studied to investigate the interaction between two different phases, such as unconventional superconductivity and magnetic order, in the quasi-2D regime19,20,21,22,23,24. Recently, it was reported that the artificial 2D rare-earth free heavy-fermion state can be realized from a 1T/1H-TaS2 heterostructure25,26. The Kondo coupling between the localized moment in the 1T-TaS2 layer and the itinerant electrons in the 1H-TaS2 layer gives rise to a heavy-fermion state. Trilayer twisted graphene was also suggested as a vdW platform for the realization of heavy-fermion physics27. However, a genuine 2D heavy-fermion state within the monolayer limit has not yet been reported.
A recent high-throughput computational study proposed 1036 easily exfoliable compounds from experimentally known compounds28. Their calculations using vdW density functional theory were validated against random phase approximation calculation and experimental results in already well-known 2D materials. This large portfolio of materials enables us to investigate the novel 2D vdW exfoliable materials with desired properties. In order to explore the potential 2D vdW heavy-fermion candidates, we considered 32 lanthanide materials containing 4f orbitals, which is the essential ingredient of the intrinsic heavy-fermion state. We believe that this is a good starting point to explore new 2D vdW heavy-fermion materials.
In this study, we investigate possible 2D vdW heavy-fermion materials based on the reported exfoliable lanthanide materials28. By analyzing the electronic structure and the Kondo resonance state, Our result reveals that the CeSiI system is the most promising 2D vdW heavy-fermion candidate. The dynamical mean-field theory calculation combined with density functional theory (DFT+DMFT) shows that the electronic properties do not change upon exfoliation and the Kondo resonance state of the CeSiI monolayer can be sensitively tuned by strain and surface doping. Based on these findings, we predict the ground state of the CeSiI monolayer in response to the external perturbation by comparing it with other well-known Ce-based heavy-fermion materials.
Results
Screening from the database
We first briefly investigate the electronic structures for 32 layered lanthanide materials proposed to be exfoliable. Not only localized f electrons but also itinerant conduction electrons are essential to forming a heavy-fermion state. Thus, one can easily get an important clue to identify heavy-fermion materials by simply checking the conduction bands at the Fermi level (EF). Therefore, we perform DFT open-core calculations, which consider f electrons as core electrons, to examine the existence of non-f conduction bands at EF.
Figure 1 shows the density of states (DOS) at EF for 32 layered lanthanide materials obtained from DFT calculation within the open-core approach. Open symbols indicate La (f0) and Lu (f14) compounds. Since they have empty or fully occupied 4f shells, the lattice Kondo effect cannot be expected. On the other hand, the compounds denoted by square symbols also cannot be heavy-fermion compounds since they exhibit an insulating nature, indicating that there are no itinerant conduction bands to screen localized 4f electrons. Finally, we are left with only four compounds (CeSiI, ErHCl, TmI2, and YbI2) satisfying the minimal necessary conditions. The four remaining candidates can be again divided into two categories. The conduction bands of CeSiI at EF are mainly coming from the ligand atoms, while those of other compounds are coming from solely lanthanide 5d orbitals.
The open-core DFT calculations were performed to check non-f contribution at EF. Materials can be classified into three different groups; insulating (squares), conduction bands (CB) from La d orbitals (triangles), and conduction bands from ligand atoms (circles). Open and filled symbols represent the materials having empty (or fully occupied) 4f orbitals and partially filled 4f orbitals, respectively.
For comparison, α-Ce is a typical heavy-fermion system whose 4f electron is screened by its own 5d orbitals. In contrast, γ-Ce, which has an isostructure with a larger volume, shows weak 4f–5d hybridization yielding a small Kondo resonance peak29,30. Since ErHCl, TmI2, and YbI2 have ligand atoms between their lanthanide atoms, the distance between the lanthanide atoms of those compounds is even greater than that of γ-Ce (3.65 Å). Therefore, 4f electrons are hardly screened by neighboring lanthanide 5d orbitals or the Kondo cloud at each lanthanide site hardly sees each other to form the coherent heavy-fermion state.
Although CeI2 is not classified into exfoliable compounds from the previous study28, it has the same structure as TmI2 and YbI2. CeI2 has a magnetically ordered ground state and the previous photoemission spectroscopy (PES) study showed that the f1 peak is almost absent at EF, indicating 4f–5d hybridization in CeI2 is much smaller than α and γ-Ce cases30. Our DFT+DMFT calculation on CeI2 also verifies the absence of a Kondo peak near EF (see Supplementary Fig. 1). Considering these aspects, we conclude CeSiI is the most promising candidate for 2D vdW heavy-fermion systems among 32 exfoliable lanthanide compounds. Very recently, it was reported that bulk CeSiI has a magnetically ordered ground state31. However, it can be sensitively tuned by external perturbations, which will be discussed in later sections.
Structural and electronic properties of CeSiI
The CeSiI vdW layer consists of a silicene layer, surrounding triangular Ce cage (orange dashed line), and outer iodine layers. The vdW gap can be defined as the iodine to iodine as depicted in Fig. 2a. The electronic structures calculated by DFT within the open-core approach are presented in Fig. 2b in terms of DOS (right) and band dispersion (left). Analysis of DOS and band dispersion leads to the following observation: (1) The iodine p state occurs primarily between −5 and −2 eV indicating that the iodine p state is fully occupied, and their contribution at EF is negligible. (2) The band dispersion near EF resembles that of pure silicene compound while the Dirac point at K point is moved to −2 eV in contrast to pure silicene, where the Dirac point is located at EF32. This indicates there is charge transfer from the Ce atom to the silicene layer. (3) Therefore, the bands crossing EF should be coming from Si px and py antibonding state. However, the contribution from Si at EF is quite small compared to the total DOS as shown in the right panel of Fig. 2b.
The most of contribution at EF is originated from the interstitial region. Figure 2c shows the calculated charge density distribution near EF (energy range −1.5 to 1.5 eV with respect to EF) for CeSiI on (110) plane (see the red thick line in the left lower panel in Fig. 2a). The electron density is delocalized all over the Ce cage (between Ce atoms and silicene layer), not localized at specific atoms. This feature agrees well with the Zintl–Klemm feature of [Ce3+I−Si−]⋅e− as suggested by the previous study33. Floating electrons on the silicene layer and the interstitial region can be the ingredient of a heavy-fermion state.
To investigate the hybridization between Ce 4f and conduction electrons (f−c hybridization) properly, DFT+DMFT calculations are performed. The calculated spectral function of bulk and monolayer CeSiI are shown in Fig. 3a at 10 K. Unlike CeI2 case, the Kondo resonance peak is clearly observed near EF, indicating substantial hybridization between Ce 4f and conduction electrons. Therefore, CeSiI is located in the vicinity of the PM heavy-fermion state. The electronic structures of bulk and monolayer CeSiI are almost identical, from which similar chemical and physical properties are expected. The temperature-dependent evolution of the Kondo resonance peak also does not change upon exfoliation as shown in the inset of Fig. 3a, b. Therefore, the CeSiI monolayer can provide an ideal platform for exploring the heavy-fermion state in the 2D monolayer limit.
Effect of strain and surface doping
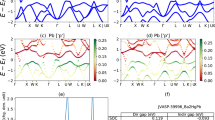
Now we investigate the external perturbation effect on the Kondo resonance state of the CeSiI monolayer. Figure 4 shows the electronic structure of the CeSiI monolayer with biaxial strain from −4% to 4%. Upon compressive (tensile) strain, the volume of the Ce cage (orange dashed line in Fig. 2a, c) surrounding the silicene layer decreases (increases). Therefore, one can easily expect stronger f−c hybridization under compressive strain due to the enhanced conduction electron density in the Ce cage. Figure 4a shows the spectral function of Ce 4f state at 10 K depending on the strain. The Kondo resonance peak is sensitively affected by the strain.
The T-dependent 4f spectral function at EF, A4f(ω = 0) is shown in Fig. 4b. The Kondo resonance peak is enhanced by the compressive strain for a wide temperature range, resulting in a higher Kondo temperature, TK energy scale. TK can be estimated from the logarithmic T dependence behavior of A4f(ω = 0) ~ ln(TK/T) (dashed line in Fig. 4b)34,35. The estimated TK for monolayer without strain is 120 K. TK slightly decreases to 110 K upon 4% tensile strain while it is strongly enhanced up to 200 K upon the compressive strain. The strain-induced f−c hybridization change is also clearly observed in the momentum-resolved spectral function as shown in Fig. 4c–e. Not only the Kondo resonance state from j = 5/2 state at EF but also those from j = 7/2 state at 0.3 eV are clearly enhanced upon the compressive strain. The kink feature at 0.3 eV above EF associated with j = 7/2−c hybridization is very weak for 4% tensile strain but it becomes much clear and stronger for compressive strain (dashed circle in Fig. 4c). In general, the kink feature in the spectral function is related to the formation of the Kondo resonance and the f−c hybridization in heavy-fermion systems36.
Another notable aspect is band-dependent f−c hybridization. This feature is most clearly observed in the case of −4% compressive strain. At the one-third point along the K−Γ line (white arrow), two dispersive bands are hybridized with Ce 4f states. However, the hybridization strengths of the two bands are quite different. One band is strongly hybridized with the Ce 4f state resulting in a large hybridization gap of 50 meV while the hybridization gap from the other band is only 10 meV. This difference arises from the different orbital character of the conduction band. The left conduction band mainly comes from Ce \({d}_{{z}^{2}}\), whereas the right band mainly comes from Si px+py orbitals (see Supplementary Fig. 2). The hybridization between Ce 4f and Si px+py states is much stronger and sensitively affected by the strain compared to the hybridization between Ce 4f and Ce \({d}_{{z}^{2}}\) state.
Next, we investigate the surface doping effect on the Kondo resonance state. There are two Ce-I layers above and below the silicene layer within a monolayer as shown in Fig. 5a. By using the virtual crystal approximation, we control the number of electrons of the upper iodine layer, mimicking the surface doping situation. The calculated Ce 4f orbitals occupancy of each upper and lower Ce layer is presented in Fig. 5b. Regardless of surface doping, Ce 4f electron occupancy remains constant for both Ce layers. However, the Kondo resonance peak of the upper Ce layer is sensitively affected by surface doping while that of the lower Ce layer does not change as shown in Fig. 5c. The surface hole doping significantly enhances only the Kondo resonance state of the upper Ce layer. This suggests that by adjusting surface doping, the Kondo resonance peaks of the upper and lower layer are separately controlled within the monolayer. In addition, I substitution by Te, CeSiI1−xTex, would be considered an effective way to enhance the Kondo resonance of CeSiI monolayer.
Phase diagram and ground state prediction
An important remaining question is how sensitive the ground state of the CeSiI monolayer can be controlled by strain or surface doping. To answer this question, we construct a phase diagram as shown in Fig. 6, by calculating the inverse DOS (1/A4f(ω = 0)) at EF (x-axis) and inverse quasiparticle lifetime Γ = −ZImΣ(0) (where Z−1 = m*/m = 1−∂ReΣ(ω)/∂ω∣ω→0) (y-axis) based on PM DFT+DMFT calculations (at T ~ 46 K) and in comparison with well-known Ce-based heavy-fermion materials as shown in Fig. 6. Both quantities of each material are normalized by those of CeCoIn5 for better comparison. The materials having PM heavy-fermion ground states are denoted by circles while those having magnetically ordered ground states are denoted by diamonds, respectively. Note that CeCoIn5 is located in the close vicinity of the QCP and magnetically ordered CeRhIn5 undergoes a superconducting transition only above 2 GPa, indicating the proximity to the QCP. Interestingly, the well-known Ce-based materials are well classified with respect to the CeCoIn5 point. The typical PM heavy-fermion systems are located below the CeCoIn5 point and magnetically ordered systems are located above the CeCoIn5. The PM ground state of CeRhIn5 under 7 GPa is also well captured8,9,37.
Along with the well-known Ce-based compounds, CeSiI monolayers with and without external perturbation (strain, surface doping, and Si substitution) are also displayed with black and open squares in Fig. 6. For the surface doping case, only the Γ and 1/A4f(ω = 0) of upper layer Ce are shown in the figure because those of lower layer Ce do not change upon surface doping on the upper iodine layer. CeSiI monolayer is located above the CeCoIn5 point, indicating a magnetically ordered ground state and it is consistent with the recent experimental result on bulk CeSiI31. It is rather located closer to CeIn3 and CeCu2Ge2. Although CeRhIn5, CeIn3, and CeCu2Ge2 have magnetically ordered ground states, they have been intensively considered as AFM heavy-fermion systems since their ground state can be easily turned into PM heavy-fermion states by external pressure or chemical doping7,8,9,10,11,12,13,14,15,16,17. Therefore, CeSiI should also be located not far from the QCP, and its ground state can be easily tuned by external perturbations like CeIn3 and CeCu2Ge2.
As we have discussed above, compressive strain and surface hole doping strongly enhance the Kondo resonance peak of the CeSiI monolayer. With 4% compressive strain, it is located right below the CeCoIn5 indicating a possible quantum phase transition to PM heavy-fermion state. With 0.1 surface hole doping, it moves further below CeCoIn5 and is located near the well-known PM heavy-fermion materials CeIrIn5 and CeCu2Si2. Therefore, CeSiI monolayer is a promising 2D vdW heavy-fermion candidate and its ground state can be tuned by strain or surface doping (or I substitution by Te), providing alternative ways to explore the QCP, magnetism, and unconventional superconductivity.
Discussion
The interesting points of this new type of heavy-fermion system are low dimensionality and frustration originating from its own triangular lattice. During the last couple of decades, the degree of quantum fluctuation has been studied in addition to the Kondo coupling and RRKY interaction. This quantum fluctuation can be enhanced by both lattice frustration and geometrical low-dimensionality. Together with the Kondo coupling strength, this new microscopic quantity (i.e., frustration) enables the construction of a 2D parameter space, zero-temperature global phase diagram38,39. So far, a complete understanding of this global phase diagram is still lacking.
By enhancing spatial dimensionality to reduce the quantum fluctuation, the cubic Ce3Pd20Si6 was studied40. One can tune Ce3Pd20Si6 from a small Fermi surface (FS) AFM state, through a large FS AFM phase, into a large FS PM state. Recently, it is reported that geometrically frustrated CePdAl hosts a stable quantum critical phase, possibly PM small FS phase. YbRh2Si241 and β-YbAlB442 also show similar quantum phase transitions. Although they do not have geometrical frustration, their quasi-2D crystal structure may enhance the quantum fluctuation and lead to a similar quantum phase transition trajectory on the global phase diagram.
However, an understanding of the microscopic processes remains missing. CeSiI monolayer can provide a new platform to study the global phase diagram. Due to its low dimensionality and lattice frustration, one can study the upper part of the global phase diagram, where the quantum fluctuation is strong. Besides, this 2D vdW heavy-fermion system has additional control parameters. In addition to magnetic field and pressure (uniform strain), uniaxial strain can be an external tuning parameter in the CeSiI monolayer. By inducing anisotropy via uniaxial strain, frustration can be controlled, providing a unique opportunity to explore the entire global phase diagram.
Another interesting aspect is the critical behavior of resistivity near this QCP with low dimensionality or frustration. In the epitaxially grown CeIn3/LaIn3 superlattice, the quantum phase transition within the 2D limit was observed by reducing the superlattice period. Near the QCP, the resistivity shows T-linear behavior deviating from the Fermi liquid behavior ρ(T) = ρ0 + ATα, where α = 2. This linear T-dependence (α = 1) is also in contrast to the resistivity behavior observed near the pressure-induced QCP in the bulk CeIn3 (α = 1.5)18. YbRh2Si2 also shows T-linear resistivity near the QCP41,43, while β-YbAlB4 recovers the Fermi liquid behavior (α = 2) at a very low temperature42. Therefore, it would be interesting to study the resistivity behavior in the CeSiI monolayer to further understand the strange metallic behavior in the global phase diagram.
Finally, the CeSiI monolayer is a new building block to study emergent phenomena in vdW heterostructures. Although 1T/1H-TaS2 heterostructure and twisted trilayer graphene can also be 2D heavy-fermion building blocks, delicate preparation is required since those heavy-fermion states are not intrinsic. It would be interesting to study vdW heterostructures which consist of CeSiI monolayer and other 2D vdW components, including magnetic materials. Although the epitaxially grown Kondo superlattice, such as CeCoIn5/CeIn3 and CeCoIn5/CeRhIn5, have been used to study the dimensionality effect and the interactions between heavy-fermion state (or superconducting state) and magnetism (bosonic excitations)22,23, CeSiI monolayer provides more degrees of freedom to make various interfaces in combination with other 2D vdW materials or substrates.
To summarize, we have investigated 2D vdW heavy-fermion systems from the experimentally known bulk compounds by using DFT+DMFT calculations. Among them, CeSiI is the most promising candidate. We have found that the Kondo coupling strength of CeSiI does not change upon exfoliation and can be easily controlled by strain and surface doping. Finally, we have predicted the ground state of the CeSiI monolayer in response to external perturbations. Although the CeSiI monolayer has a magnetically ordered ground state, we found that the compressive strain and surface hole doping strongly enhance the Kondo coupling strength, indicating a possible quantum phase transition to PM heavy-fermion state. Our result thus suggests that the CeSiI monolayer can be a genuine 2D vdW heavy-fermion system and provide a new playground to study the QCP and emergent phenomena in vdW heterostructures.
Methods
DFT and DFT+DMFT calculations
We first performed DFT open-core calculation using the Vienna ab-initio Simulation Package (VASP) for the screening process44. The experimental crystal structure of 32 lanthanide materials employed from the Inorganic Crystal Structure Database (ICSD) was used in the calculations. For structural relaxations of the strained CeSiI cases, DFT open-core calculations with VASP were also employed since DFT calculations with 4f orbitals significantly overestimate f−c hybridization, resulting in a smaller lattice constant. DFT open-core calculation with vdW correction well reproduced the experimental crystal structure of CeSiI. The internal atomic positions were fully relaxed for biaxial strained case, while the CeSiI monolayer structure was just adopted for surface doping cases.
To study the f−c hybridization properly, we employed a DFT+DMFT calculation as implemented in DFT+Embedded DMFT (eDMFT) Functional code45. DFT calculations were performed by using WIEN2k code46 and the correlation effect of Ce 4f orbitals is treated by a DMFT loop. The hybridization energy window from −10 to 10 eV with respect to the EF was chosen and U = 5 eV and J = 0.68 eV were used for all Ce-based compounds. The continuous-time quantum Monte Carlo (CTQMC) solver was basically adopted for all calculations (Fig. 6)47. The temperature evolution of the Kondo resonance peak on the real axis was analyzed by using vertex corrected one-crossing approximation (OCA) solver to avoid the ambiguity arising from analytic continuation, which is inevitable for the CTQMC solver (Figs. 3 and 4)45.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270 (2017).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265 (2017).
Bonilla, M. et al. Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates. Nat. Nanotechnol. 13, 289 (2018).
O’Hara, D. J. et al. Room temperature intrinsic ferromagnetism in epitaxial manganese selenide films in the monolayer limit. Nano Lett. 18, 3125 (2018).
Kim, K. et al. Large anomalous Hall current induced by topological nodal lines in a ferromagnetic van der Waals semimetal. Nat. Mater. 17, 794 (2018).
Seo, J. et al. Nearly room temperature ferromagnetism in a magnetic metal-rich van der Waals metal. Sci. Adv. 6, eaay8912 (2020).
Hegger, H. et al. Pressure-induced superconductivity in quasi-2D CeRhIn5. Phys. Rev. Lett. 84, 4986 (2000).
Park, T. et al. Hidden magnetism and quantum criticality in the heavy fermion superconductor CeRhIn5. Nature 440, 65 (2006).
Seo, S. et al. Controlling superconductivity by tunable quantum critical points. Nat. Commun. 6, 6433 (2015).
Jiao, L. et al. Fermi surface reconstruction and multiple quantum phase transitions in the antiferromagnet CeRhIn5. Proc. Natl. Acad. Sci. USA 112, 673 (2015).
Küchler, R. et al. Quantum criticality in the cubic heavy-fermion system CeIn3−xSnx. Phys. Rev. Lett. 96, 256403 (2006).
Sebastian, S. E. et al. Heavy holes as a precursor to superconductivity in antiferromagnetic CeIn3. Proc. Natl. Acad. Sci. USA 106, 7741 (2009).
Knebel, G., Braithwaite, D., Canfield, P. C., Lapertot, G. & Flouquet, J. Electronic properties of CeIn3 under high pressure near the quantum critical point. Phys. Rev. B 65, 024425 (2001).
Iizuka, T., Mizuno, T., Hun Min, B., Seung Kwon, Y. & Kimura, S.-i Existence of heavy fermions in the antiferromagnetic phase of CeIn3. J. Phys. Soc. Jpn. 81, 043703 (2012).
Yamaoka, H. et al. Role of valence fluctuations in the superconductivity of Ce122 compounds. Phys. Rev. Lett. 113, 086403 (2014).
Yuan, H. et al. Observation of two distinct superconducting phases in CeCu2Si2. Science 302, 2104 (2003).
Ren, Z. et al. Giant overlap between the magnetic and superconducting phases of CeAu2Si2 under pressure. Phys. Rev. X 4, 031055 (2014).
Shishido, H. et al. Tuning the dimensionality of the heavy fermion compound Celn3. Science 327, 980 (2010).
Mizukami, Y. et al. Extremely strong-coupling superconductivity in artificial two-dimensional Kondo lattices. Nat. Phys. 7, 849 (2011).
Shimozawa, M. et al. Controllable Rashba spin–orbit interaction in artificially engineered superlattices involving the heavy-fermion superconductor CeCoIn5. Phy. Rev. Lett. 112, 156404 (2014).
Goh, S. K. et al. Anomalous upper critical field in CeCoIn5/YbCoIn5 superlattices with a Rashba-type heavy fermion interface. Phys. Rev. Lett. 109, 157006 (2012).
Naritsuka, M. et al. Tuning the pairing interaction in a d-wave superconductor by paramagnons injected through interfaces. Phys. Rev. Lett. 120, 187002 (2018).
Naritsuka, M. et al. Coupling between the heavy-fermion superconductor CeCoIn5 and the antiferromagnetic metal CeIn3 through the atomic interface. Phys. Rev. B 100, 024507 (2019).
Naritsuka, M., Terashima, T. & Matsuda, Y. Controlling unconventional superconductivity in artificially engineered f-electron kondo superlattices. J. Phys.: Condens. Matter 33, 273001 (2021).
Vaňo, V. et al. Artificial heavy fermions in a van der Waals heterostructure. Nature 599, 582 (2021).
Ruan, W. et al. Evidence for quantum spin liquid behaviour in single-layer 1T-TaSe2 from scanning tunnelling microscopy. Nat. Phys. 17, 1154 (2021).
Ramires, A. & Lado, J. L. Emulating heavy fermions in twisted trilayer graphene. Phys. Rev. Lett. 127, 026401 (2021).
Mounet, N. et al. Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds. Nat. Nanotechnol. 13, 246 (2018).
Kim, J. et al. Topological phase transition in the archetypal f-electron correlated system of cerium. Phys. Rev. B 100, 195138 (2019).
Jungmann, A. et al. Photoemission of LaI2 and CeI2. Z. Phys. B 97, 25 (1995).
Okuma, R., Ritter, C., Nilsen, G. J. & Okada, Y. Magnetic frustration in a van der Waals metal CeSiI. Phys. Rev. Mater. 5, L121401 (2021).
Cahangirov, S., Topsakal, M., Aktürk, E., Şahin, H. & Ciraci, S. Two- and one-dimensional honeycomb structures of silicon and germanium. Phys. Rev. Lett. 102, 236804 (2009).
Mattausch, H. & Simon, A. Si6, Si14, and Si22 Rings in iodide silicides of rare earth metals. Angew. Chem. Int. Ed. 37, 499 (1998).
Choi, H. C., Min, B. I., Shim, J. H., Haule, K. & Kotliar, G. Temperature-dependent Fermi surface evolution in heavy Fermion CeIrIn5. Phys. Rev. Lett. 108, 016402 (2012).
Kang, H., Haule, K., Kotliar, G., Coleman, P. & Shim, J.-H. Energy scales of the doped Anderson lattice model. Phys. Rev. B 99, 165115 (2019).
Choi, H. C., Haule, K., Kotliar, G., Min, B. I. & Shim, J. H. Observation of a kink during the formation of the Kondo resonance band in a heavy-fermion system. Phys. Rev. B 88, 125111 (2013).
Kumar, R. et al. The crystal structure of CeRhIn5 under pressure. Phys. B: Condens. Matter 359–361, 407 (2005).
Si, Q. Global magnetic phase diagram and local quantum criticality in heavy fermion metals. Phys. B: Condens. Matter 378–380, 23 (2006).
Si, Q. Quantum criticality and global phase diagram of magnetic heavy fermions. Phys. Status Solidi (b) 247, 476 (2010).
Custers, J. et al. Destruction of the Kondo effect in the cubic heavy-fermion compound Ce3Pd20Si6. Nat. Mater. 11, 189 (2012).
Friedemann, S. et al. Detaching the antiferromagnetic quantum critical point from the Fermi-surface reconstruction in YbRh2Si2. Nat. Phys. 5, 465 (2009).
Tomita, T., Kuga, K., Uwatoko, Y., Coleman, P. & Nakatsuji, S. Strange metal without magnetic criticality. Science 349, 506 (2015).
Nguyen, D. et al. Superconductivity in an extreme strange metal. Nat. Commun. 12, 1 (2021).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Haule, K., Yee, C.-H. & Kim, K. Dynamical mean-field theory within the full-potential methods: electronic structure of CeIrIn5, CeCoIn5, and CeRhIn5. Phys. Rev. B 81, 195107 (2010).
Blaha, P. et al. WIEN2k: an APW+lo program for calculating the properties of solids. J. Chem. Phys. 152, 074101 (2020).
Haule, K. Quantum Monte Carlo impurity solver for cluster dynamical mean-field theory and electronic structure calculations with adjustable cluster base. Phys. Rev. B 75, 155113 (2007).
Acknowledgements
B.G.J. thanks Junwon Kim and Young-Woo Son for the fruitful discussion. Work at Los Alamos was carried out under the auspices of the U.S. Department of Energy (DOE) National Nuclear Security Administration (NNSA) under Contract No. 89233218CNA000001. It was supported by UC Laboratory Fees Research Program (Grant Number: FR-20-653926) and in part by the Center for Integrated Nanotechnologies, a DOE BES user facility. J.H.S. and C.L. were supported by the National Research Foundation of Korea (NRF) grant funded by the Korea Government (Grant Nos. 2020R1A5A1019141, 2020M3H4A2084418, 2021R1A2C2010972, 2021R1F1A1063478, and 2022M3H4A1A04074153).
Author information
Authors and Affiliations
Contributions
B.G.J. conceived the work. B.G.J. performed the DFT and DFT+DMFT calculations and analyzed the calculation results together with C.L., J.H.S., and J.-X.Z. All authors discussed the results and participated in the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jang, B.G., Lee, C., Zhu, JX. et al. Exploring two-dimensional van der Waals heavy-fermion material: Data mining theoretical approach. npj 2D Mater Appl 6, 80 (2022). https://doi.org/10.1038/s41699-022-00357-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-022-00357-x
This article is cited by
-
A quantum collaboration for flat bands
Nature Physics (2024)
-
Two-dimensional heavy fermions in the van der Waals metal CeSiI
Nature (2024)
-
Two-dimensional heavy fermion in a monoatomic-layer Kondo lattice YbCu2
Nature Communications (2023)