Abstract
The layered transition-metal dichalcogenide WTe2 is characterized by distinctive transport and topological properties. These properties are largely determined by electronic states close to the Fermi level, specifically to electron and hole pockets in the Fermi sea. In principle, these states can be manipulated by changes to the crystal structure. The precise impact of particular structural changes on the electronic properties is a strong function of the specific nature of the atomic displacements. Here, we report on time-resolved X-ray diffraction and infrared reflectivity measurements of the coherent structural dynamics in WTe2 induced by femtosecond laser pulses excitation (central wavelength 800 nm), with emphasis on a quantitative description of both in-plane and out-of-plane vibrational modes. We estimate the magnitude of these motions, and calculate via density functional theory their effect on the electronic structure. Based on these results, we predict that phonons periodically modulate the effective mass of carriers in the electron and hole pockets up to 20%. This work opens up new opportunities for modulating the peculiar transport properties of WTe2 on short time scales.
Similar content being viewed by others
Introduction
Layered transition-metal dichalcogenides are an important class of materials, structurally characterized by the formation of quasi-two dimensional, buckled atomic layers that are connected to each other via weak van der Waals forces. A prominent example of such a material is tungsten ditelluride (WTe2). At standard conditions, WTe2 crystallizes in the non-inversion-symmetric orthorhombic space group Pmn21 (Td)1. In this phase the material hosts a number of interesting and promising properties, including an extremely large and non-saturating magnetoresistance2, possible type-II Weyl semimetal character3, quantum spin hall effect4 and room-temperature ferroelectricity5. These characteristics are strongly linked to the underlying structure, which suggests that selective modifications to the structure may offer a way to modulate these emergent properties.
Although such peculiar structural modifications are difficult to achieve in equilibrium, it is possible to generate a variety of transient structural changes using ultrashort optical pulses. In particular, these pulses are able to generate “coherent phonons”, i.e., vibrations with a well-defined phase with respect to the triggering optical pulse, and often large amplitude6,7,8. These vibrations can actively modulate the optical and transport properties of materials in a non-equilibrium condition9.
WTe2 exhibits several vibrational modes that can be excited coherently by ultrafast laser excitation7,8. Among others, an optical mode at 0.24 THz, with a coherence time of several tens of picoseconds, is particularly significant. It involves an anti-phase motion of adjacent layers along an in-plane crystallographic axis, reminiscent of a high-frequency acoustic shear mode. Exciting the structure along the shear mode has been proposed as a method to control topology via a modification of the number and type of Weyl points3,10,11,12,13, moving towards an inversion-symmetric metastable state with trivial topology, as observed by Sie et al.10 using ultrafast electron diffraction and second-harmonic-generation spectroscopy. Other, higher-frequency, coherent optical modes involve both in- and out-of-plane motion and decay on a time scale significantly faster than the shear mode. While they are not able to move the structure toward an inversion-symmetric state by themselves, they are coupled to the electronic structure and can have a potentially strong influence on transport and optical properties. Although signatures of their influence on the electronic structure have been revealed in previous works8,14, their impact has not been fully explored, partially due to a limited amount of information regarding the achievable magnitude of these vibrations. To provide this information, direct structural probes with sufficient time resolution are required.
Pump-probe diffraction using ultrashort X-ray or electron pulses is one possible experimental route to address this problem. The excitation of zone-center optical modes in WTe2 results in coherent modulation of the structure factor, which, in turn, modulates the intensity of diffraction peaks15. Since the contribution given by each optical mode varies with the momentum transfer of the diffraction peak, systematic measurement of several diffraction peaks yields quantitative information on mode frequencies, eigenvectors and displacement amplitudes16. These experiments require access to X-ray pulses with durations on the order of 100 fs or shorter, providing the necessary time resolution to reveal the high-frequency modes. X-ray free-electron laser (FEL) facilities are particularly well-suited to perform such experiments.
In this work, we quantify the coherent structural dynamics of WTe2 that result from excitation with a near-infrared (800 nm) pump pulse using ultrafast X-rays derived from the SwissFEL free-electron laser17. We compare our findings with those from complementary time-resolved near-infrared reflectivity measurements, and we estimate through density functional theory (DFT) calculations the impact of these structural perturbations on the electronic structure. We show that the coherent atomic motion perturbs the semimetallic pockets, leading to a periodic change of their energy levels and associated effective masses. For the experimentally determined phonon amplitudes we estimate a relative change of the effective mass up to ±20% in specific regions of the hole and electron pockets.
These structural modulations are followed by long-lived changes of the average unit cell structure, the Debye-Waller factor and strain that likely arise from an incoherent heating of the lattice on long time scales.
Results
Time-resolved X-ray diffraction (TRXD)
In order to estimate the amplitude of coherent optical vibrations induced by the infrared laser pulse, we measure the changes in the intensity of a selected number of X-ray diffraction peaks (see in “Methods”). Figure 1c shows these data acquired over a time range of ~30 ps for the peaks (075), \((\bar{1}46)\), \((\bar{1}62)\), and \((\bar{1}63)\) for an absorbed fluence of a 3.2 mJ/cm2. The intensity variation is represented as ΔI/I, defined as the ratio between the diffraction intensity variation due to the pump excitation and the intensity in equilibrium conditions.
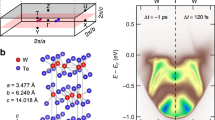
a Scheme of the time-resolved X-ray diffraction experiment. b WTe2 crystal structure projected in the yz plane where the red rectangles delimit the orthorhombic unit cell; the atomic labels are used for discussion in the text. c Time-resolved modification of the diffraction intensity ΔI/I for the (075), \((\bar{1}46)\), \((\bar{1}62)\), and \((\bar{1}63)\) diffraction peaks, where the traces are shifted for visualization purposes, and d for the \((\bar{1}63)\) reflection using a tenfold shorter time step; in the latter panel, the fit model takes into account four oscillatory contributions (see text). In the graphs, the markers correspond to experimental data, while the continuous lines are the fit curves. e Fourier transform of panel d after subtracting the non-oscillatory response; the right part of the curve multiplied was by 3 to highlight the peaks indicated by the black arrows. The data were acquired at 3.2 mJ/cm2 absorbed fluence at T = 295 K. The error bars represent one standard deviation uncertainty.
At t = 0, where pump and probe are superimposed in time, the peak intensities start to deviate from the equilibrium value with the clear appearance of a 0.24 THz modulation. This oscillation decays with a time scale of tens of picoseconds. Using a smaller time step (Fig. 1d) for peak \((\bar{1}63)\), higher-frequency modes emerge as well.
We fit the experimental data with the empirical expression
where \(H(t)=[S* G](t)\) is a convolution itself,
represents the binning of the relative delays into intervals of width τbin, taking into account the X-ray/infrared jitter within the time step, and G(t) is a Gaussian function representing the probe pulse temporal shape. The chosen value of τbin varies with pump-probe delay, ranging from 50 fs near t = 0 to 500 fs at much later pump-probe delays. These bin values are larger than the FWHM duration of the pump pulse (τFWHM = 35 fs). The system response due to the pump perturbation is modeled as
θ(t) is the Heaviside function, which we use to approximate the change in the electronic state occupation due to the pump pulse, here justified since the pump pulse duration is significantly shorter than the expected time scales of electronic relaxation6. The parameters A and B approximate contributions from the pump-induced aperiodic atomic reorganization and thermal motion. The index i runs over a number n of different oscillatory modes with amplitudes Ci, angular frequencies ωi = 2πfi, initial phases ϕi and time-decay constants τi. An alternative procedure, based on a displacive excitation model, is reported in the Supplementary Note 1. Figure 1e shows the Fourier transform of the data presented in Fig. 1d after subtracting the non-oscillatory components of the fit from the data. We observe several resonances, each of which can be identified with A1 zone-center optical phonon modes based on the correspondence with frequencies determined by density functional perturbation theory (DFPT) calculations (see Supplementary Note 2). The two highest-frequency oscillations, labeled 3 and 4, have frequencies with values close to those of several A1 modes and so it is not possible to uniquely identify them. Indeed, the fact that several distinct modes may contribute to these oscillations may explain the larger width of the corresponding peak in the Fourier transform.
Using the empirical model (Eq. (1)) to fit the experimental data in Fig. 1c, we obtain a shear mode frequency 0.244 ± 0.002 THz and a time-decay constant of 26 ± 9 ps. From the \((\bar{1}63)\) dynamics reported in Fig. 1d we find another prominent mode with a frequency of 2.392 ± 0.004 THz and a lifetime of 4.6 ± 0.8 ps. Other oscillatory contributions, using in total four damped cosine terms, were found at 3.41 ± 0.02 THz and 6.14 ± 0.07 THz. The last mode only marginally contributes in the first few hundreds of femtoseconds (see Supplementary Note 1). The results are summarized in Table 1. The uncertainties reported here and elsewhere in this work are equivalent to one standard deviation.
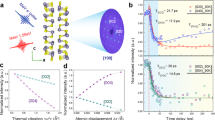
These dynamics change with the excitation fluence. Figure 2a reports the fluence dependence for \((\bar{1}46)\) in the 1.6 − 3.2 mJ/cm2 range. Figure 2b, c show the fluence dependence of some of the parameters resulting from a fit to Eq. (1). These figures show a clear quasi-linear enhancement of the shear mode amplitude together with a minor redshift on increasing fluence. At the same time, there is a pronounced decrease of time-decay constant τ1 (see Supplementary Note 3).
Figure 3a, b shows the fluence dependence for data collected at the \((\bar{1}63)\) reflection in the 3.2−9.6 mJ/cm2 range for two separate time windows. Figure 3c, d shows the fluence dependence of the amplitude and frequency parameters from a fit to Eq. (1). Since the 6.14 THz mode contribution is small with respect to the others (see peak 4 in Fig. 1e and Supplementary Note 1); here we used a three-phonon model to limit the number of free parameters. We observe that the shear mode amplitude decreases with fluence in this range, differently from the other modes.
The frequencies of the modes show a small redshift as the fluence increases, aside from the shear mode where frequency variation is rather small. The time-decay constants show no clear trend with fluence, in contrast to the behavior observed for the \((\bar{1}46)\) reflection in a lower fluence range (see Fig. 2 and Supplementary Note 3).
Time-resolved near-infrared reflectivity
Time-resolved reflectivity traces, acquired using 800 nm pump and 950 nm probe wavelengths with 250 kHz repetition-rate laser (see details in “Methods”), are reported in Fig. 4a. The non-equilibrium reflectivity is expressed as ΔR/R, i.e., the ratio between the reflectivity difference due to the presence of the pump pulse and the equilibrium value. At time zero (t = 0), ΔR/R quickly decreases with a subsequent partial recovery, which becomes slower as the fluence is increased, then reaching a quasi-equilibrium plateau in the investigated time window.
a Experimental data; fit results for b maximum ΔR/R variation (left axis, green) and its time position with respect to the one at the lowest fluence (right axis, black), c initial amplitude for the shear mode (left axis, red) and for the second-lowest A1 mode (right axis, blue), d shear mode (left axis, red) and second-lowest A1 mode frequencies (right axis, blue), e second-lowest A1 mode time-decay constant. The error bars represent one standard deviation uncertainty.
This description becomes less appropriate as the fluence grows: a saturation of the first drop occurs together with a time shift of the maximum reflectivity change (Fig. 4b) and a pronounced slower ΔR/R decrease sets in at about 5 ps after the initial dynamics are over.
We model the reflectivity changes as
where
represents electronic effects, and
represents the influence of structural changes in manner analogous to Eq. (3). In Eq. 5, Cr represents the pump-probe cross-correlation and \({A}_{k}^{\prime}\) are amplitude and τr,k time-decay constants related to electronic relaxation phenomena6. In Eq. 6, A″ and B″ are additional background terms related to slower electronic relaxation phenomena, while \({C}_{i}^{\prime}\), \({\omega }_{i}^{\prime}=2{{{\rm{\pi }}}}{f}_{i}^{\prime}\), \({\phi }_{i}^{\prime}\) and τo,i are the amplitude, angular frequency, initial phase and time-decay constant of an oscillatory response.
In Fig. 4c–e, we report the initial amplitudes, frequencies and time-decay constants. The latter for the shear mode is not included in panel e because the time-window is much shorter than the previously reported value (about 77 ps at 0.7 mJ/cm2 absorbed fluence), preventing a reliable evaluation at low fluences8. Moreover, the highest fluence in Fig. 4a was excluded in the analysis due to the high damping and small amplitude of the shear mode effects leading to a poor fit using the two exponentially damped cosine terms. At 3.2 mJ/cm2, the time-decay constant for the shear mode is found to be 27 ± 6 ps.
As the fluence increases, the amplitudes of both modes initially grow. The shear mode amplitude then rapidly decreases, while the amplitude of the 2.4 THz mode saturates. A frequency redshift is detected for both modes as the fluence grows, although a much higher relative change is observed for the shear mode. Finally, the decay time of both modes decreases with higher fluences. The fluence dependence of time-resolved near-infrared reflectivity shows a saturation of the maximum ΔR/R variation for the highest investigated fluences (Fig. 4b). Above these values, we found that for a ≈ 9.1 mJ/cm2 absorbed fluence, the near-infrared response is gradually, but permanently, modified (see Supplementary Note 4).
Numerical simulations
WTe2 has an orthorhombic Brillouin zone with semimetallic electron and hole pockets centered on the Γ-X direction, which determine several of its properties2,3. The hole pockets are closer to Γ, while the electron pockets are closer to X. The relative size of the electron and hole pockets in the simulations is comparable with that expected at room-temperature where the electron carriers dominate18.
The coherent phonon dynamics in WTe2 directly impact the bandstructure and, consequently, the optical properties of the system; their spectral dependence can be reproduced with a displacive model starting from the relaxed equilibrium configuration derived from DFT calculations8,14. The coherent optical phonon response retains analogous time-dependent characteristics over the entire range shown in Fig. 4, which overlaps with the fluence values employed in the ultrafast X-ray measurements and in the cited works. Consequently, we follow an analogous approach to study in detail the electronic structure modifications (see “Methods”). We focus on the two most prominent modes at the lowest frequencies among the A1 zone-center optical phonons, i.e., the 0.24 THz (shear) and the 2.4 THz modes. A full gallery of the A1 zone-center eigendisplacements is reported in Supplementary Note 2.
Coherent displacement of the lattice along the eigendisplacements of each mode leads to distinct modifications of the electronic structure. To focus on the most significant changes, we selected specific maxima and minima of the bandstructure close to the Fermi level (Fig. 5d), relevant for the transport properties, and calculate the absolute effective mass19
where + and – are used for electron-like and hole-like bands, respectively, and ε(k) is the energy-momentum dispersion relation. Each electronic dispersion was fitted using a 6th order polynomial expression around the extrema. The effective mass values were extracted at the point where the first derivative is zero. In the following, we will limit our discussion to the diagonal components i = j = x, which are the most relevant when considering the magnetoresistance effects2. The electronic dispersion along the \(\hat{{{{{\bf{k}}}}}_{{{{\bf{y}}}}}}\) and \(\hat{{{{{\bf{k}}}}}_{{{{\bf{z}}}}}}\) directions is generally much flatter than for \(\hat{{{{{\bf{k}}}}}_{{{{\bf{x}}}}}}\), leading to heavier effective masses around the examined k-points in those directions, limiting the electron/hole mobility (see Supplementary Note 2 and20,21). We report the numerically averaged shear mode displacement, i.e., along the y-coordinate, for the atoms from the DFPT calculations, while the 2.4 THz modifications are presented as the z-shift of one of the tungsten atoms (W#1 as tagged in Fig. 5b, c).
a Fermi surface of WTe2 plotted using FermiSurfer57. The color scale indicates the modulus of the Fermi velocity. Coherent optical phonons at b ≈0.24 THz (shear mode) and c ≈ 2.4 THz as derived from DFPT and plotted using XCrySDen58. d Band dispersion along X* (0.3 0 0) – Γ (0 0 0) around the Fermi level. Selected interesting regions are highlighted for the following analysis. e Example of band structures modifications at P1 due to the phononic displacements (from –700 to 700 fm with the steps shown in panel g, i. f–i Effective mass changes around P1 (0.228 0 0), P2 (0.123 0 0), P3 (0.117 0 0), and P4 (0.093 0 0); these coordinates are expressed in reciprocal lattice units. W#1 refers to the labeling for the unit cell atoms reported in Fig. 1b.
In contrast to the shear mode, which is a uniform anti-phase shift of subsequent layers, the 2.4 THz phonon involves non-uniform y- and z-shifts, which perturb the intralayer covalent bonds between the atoms.
In Fig. 5f–i, we show the effective mass variations linked to the phononic shifts. For each spot highlighted in Fig. 5d, we present the results in terms of the percentage change in the effective mass. The individual band oscillations together with the equilibrium electronic bands are showcased in Supplementary Note 2. At P1, where the electron pocket has its energy minimum, the bands are almost unaffected by the shear mode, while for the other examined regions, the shear effects are much more pronounced (Fig. 5f, h).
The DFT calculations used to estimate the effective mass changes reported in Fig. 5 do not consider electron correlations. The inclusion of Hubbard and other many-body corrections has, however, been reported to improve the agreement with experimental observations in the case of a similar layered dichalcogenide such as MoTe222,23. Regarding WTe2, it has been shown that many-body effects can perturb the shape of the calculated bands24, although experimental validation of these changes is particularly challenging due to the high-resolution requirements and the fact that small changes in the growth process can have a significant impact on the magnetoresistance and other transport properties associated with the electronic states close to the Fermi level2,25,26. Nonetheless, we repeated our calculations with an approach going beyond the standard ground-state density functional theory, DFT + U, to approximate the effects of Hubbard correlations and obtain substantially similar results (see Supplementary Note 2).
Discussion
When a material is subjected to a displacive excitation mechanism, the excitation of electrons from their ground state drives the system into a new transient configuration, which involves reorganization of the atomic coordinates. In principle, the photon excitation involves a large number of electronic states; nonetheless, the removal of electrons from the states close to the Fermi level, in particular from the electron and hole pockets bands, is believed to be the driving mechanism of the shear mode bringing the system towards the centrosymmetric 1T’(*) phase10,12,27.
The coherent X-ray diffraction intensity is directly related to the distribution of the atoms in the unit cell28. In general, for a (hkl) reflection, the structure factor is
where Ghkl is the modulus of the reciprocal lattice vector, λ is the X-ray wavelength, fj(Ghkl, λ) is the atomic form factor and uxj, uyj, uzj are the coordinates in the unit cell for the j-th atom of the basis normalized by the corresponding lattice parameter. The atomic form factors can be obtained from the model and data found in refs. 29,30 including the first-order corrections due to the X-ray photon energy28. In the kinematic approximation, the diffracted intensity is then proportional to \({\left|S({G}_{hkl},\lambda )\right|}^{2}\).
The estimate of the coherent phonon amplitudes using the X-ray diffraction data was performed as follows. The relaxed structure from the DFT calculation was perturbed by stretching it along the phonon eigendisplacements found through DFPT. As a function of the displacement amplitude, diffraction intensity curves with respect to the equilibrium value (ΔI/I) were calculated for the examined peaks. The initial amplitudes of the modes were then found by interpolation comparing the empirical fit data with the calculated values. When data of multiple peaks were available, e.g., in Fig. 1c, the amplitude was averaged over the individual peak results. For the 3.2 mJ/cm2 fluence, we obtained 3.3 ± 1.0 pm for the oscillation amplitude of the 0.24 THz shear mode along the y-axis and a 218 ± 15 fm amplitude along the z-axis direction associated with the 2.4 THz mode for the tungsten atoms W#1 (Fig. 1b). For the electronic bands analyzed in Fig. 5f–i, the effects are as large as 20% for the shear mode and 10% for the 2.4 THz mode.
Differences among the amplitude values derived from the individual peaks in Fig. 1c can be attributed to the limitations of the DFPT as well as small variations of the optical penetration depth with respect to the crystalline axes (see Supplementary Note 5) and of the X-ray penetration angle among the investigated peaks, which affect the recorded diffraction intensity variation16.
The coherent response in the reflectivity data shows analogous trends to the ones observed in the semimetal bismuth31. As the deposited energy is increased, the transient electronic and lattice temperature grow accordingly, leading to shorter coherent phonon decay times connected to three-phonon decay processes, or higher when favored by elevated temperatures giving larger phonon occupations. Moreover, the damping of the modes is expected to increase due to larger anharmonic effects as the atoms are driven further away from the bottom of the interatomic potential well and thus from the harmonic approximation.
Comparing the coherent phonon parameters obtained from the X-ray diffraction and near-infrared reflectivity datasets (Figs. 2b, 3c, 4c), we notice that the phonon amplitudes follow an analogous trend. However, a better agreement is found with the reflectivity results for close, albeit lower, fluences. This can be understood by considering a probe depth longer than the pump penetration in the diffraction study, in contrast to the near-infrared reflectivity experiment where they are almost matched (see “Methods” and Supplementary Note 5). In fact, the pump absorption along the direction perpendicular to the surface leads to different excitation levels at different depths. This effect also contributes to the discrepancy of the phonon frequencies dependence on the absorbed fluence. In this case, a redshift was clearly resolved in the near-infrared data Fig. 4d, while the frequency value undergoes only minor changes in the fluence range examined in the X-ray experiment (Figs. 2c and 3d). A more advanced analysis of this effect would require, however, a study of the X-ray incidence angle dependence16.
The coherent shear motion does not heavily perturb the electronic density associated with the covalent bonds, but rather the interlayer region influenced by the weaker van der Waals interactions. This is likely the reason why the shear mode damping time constant is much longer than the higher-frequency modes, which instead perturb the electronic density around the bonds. This different impact on the charge distribution leads to much larger changes in the bandstructure when considering higher-frequency modes with respect to the shear mode under comparable strain amplitudes. Charge-density maps are provided in Supplementary Note 2 together with Helmholtz free energy curves showing the larger impact of the 2.4 THz mode for comparable displacements along the y-direction. Interestingly, the parabolic potential of a harmonic oscillator is much more suited for the 2.4 THz mode even at high displacements, while for a uniform shear displacement the free energy curve has a double-well shape. The local maximum configuration is close to the 1T’(*) structure with inversion symmetry10.
As shown in Fig. 5f–i, coherent displacements of this magnitude are predicted to affect strongly the effective mass of carriers near the Fermi level. This last property for these bands has a large influence on transport properties, in particular the carrier mobility. This is evidenced by previous experimental and theoretical work on WTe2 that has demonstrated the impact mechanical strain can have on both electronic bandstructure and magnetoresistance8,32. Using a simple deformation-potential-based model33, we can estimate the relationship between mobility and effective mass within a single band as \({\mu }^{{{{\rm{bulk}}}}}\propto {({m}^{* })}^{-5/2}\). Owing to this relationship, even small changes in the effective mass can have a large impact on the magnetoresistance2. In fact, for the case of perfect electron and hole carrier compensation, the magnetoresistance is given by \({{{\rm{MR}}}}={\mu }_{{{{\rm{e}}}}}^{{{{\rm{bulk}}}}}{\mu }_{{{{\rm{h}}}}}^{{{{\rm{bulk}}}}}{B}_{{{{\rm{m}}}}}^{2}\), where “e” and “h” refer to the electron and hole species and Bm is the magnetic field amplitude. This suggests that in laser-excited WTe2 coherent phonons periodically modulate both the mobility and magnetoresistance.
These transport properties would, at least for short times after excitation, also be strongly influenced by the transient electronic excitation of the material. This may suppress the potential influence of the coherent phonons on the transient carrier dynamics. We note, however, that the shear mode oscillations persist on time scales of 25 ps, much longer than the time scales for both carrier relaxation and quasi-thermalization6,8. The Fermi velocity in WTe2 is estimated as ≈ 2 ⋅ 105 m/s with moderate anisotropy34,35. This implies that in high-quality samples with sufficiently uniform excitation, carriers can travel for hundreds of nanometers over time scales small compared to the ≈ 4 ps period of the shear mode. Such sample quality has been demonstrated as feasible, with measured carrier mean free paths of several microns for in-plane directions35,36,37.
The idea of such ultrafast and large-scale modulations of transport properties might be an interesting direction to pursue in thin-film devices based on WTe2, with possible applications in THz and sub-THz electronics and photonics. It is reported in several works38,39,40 that films of WTe2 have a very high magnetoresistance even down to ≈ 30 nm thickness. This roughly matches the intensity penetration depth at 800 nm (see Supplementary Note 5), which suggests that it is possible to uniformly excite such a film. The depth limitation could be further lifted by employing a lower photon energy pump with a larger penetration depth, which was shown to efficiently launch the shear mode as well. Lower photon energy pumps may also help to mitigate heating effects; for example, excitation at 0.6 eV photon energy has been predicted to lead to a larger initial shear displacement10,12. It has also been shown via optical measurements that these coherent phonons are also excited at lower sample temperatures where the magnetoresistance is much higher2,6,7,8. It may also be fruitful to explore the influence of doping on the dynamics, since the magnetoresistance is highly sensitive to the balance between electron and hole densities18.
In addition to the oscillatory dynamics, the data also show marked non-oscillatory time-dependent changes in diffraction efficiency. Our measurements of the diffracted intensity as a function of rotation angle ϕ about the sample surface normal (see Fig. 1a and Supplementary Note 3) show small changes in the optimal diffraction conditions that are consistent with an expansion of the unit cell caused by a transient temperature increase31,41,42. Such an increase in temperature is also expected to decrease the overall peak intensity because of an accompanying increase in ionic disorder (Debye-Waller factor)28,43. An increase in local temperature may also quasi-statically alter the relative position of ions within the unit cell, resulting in a change in structure factor that is highly dependent on the reflection. For the \((\bar{1}62)\) reflection we observe an overall increase in the diffraction efficiency at time delays longer than 25 ps, whereas at similar times we registered a marked decrease for \((\bar{1}63)\) (Supplementary Figs. 3d, g in Supplementary Note 3). Differently, measurements of the \((\bar{1}46)\) and (075) reflections show evidence of only a shift, but with a negligible overall diffraction efficiency change (Supplementary Fig. 3c, h in Supplementary Note 3). These longer-term modifications of the structure factor are consistent with the change of the structure along the shear mode coordinate towards the centrosymmetric 1T’(*) phase proposed by Sie et al.10 and supported by recent time-dependent density functional theory and molecular dynamics simulations12.
In summary, we studied the structural response of WTe2 to a 800 nm light excitation with particular focus on coherent phonon modes. This collective motion has a significant impact on the electronic properties of the material leading to measurable changes in the energy levels and, consequently, the optical properties. In particular, the electronic bandstructure is subjected to a non-uniform change of the energy levels, which modifies the curvature of the bands close to the Fermi level leading to a variation of the effective masses. The impact of the coherent phonon oscillations is expected to influence various transport properties such as electrical transport through a high-frequency modulation of its extremely high magnetoresistance2,33 and thermoelectric performance44, which is of particular interest for low effective mass systems. Such oscillations could be implemented as modulators, simple function generators and test devices for high-frequency applications, which are expected to become increasingly relevant for fast big-data transfer and telecommunications.
Methods
Sample
Our WTe2 sample, grown by HQ Graphene45, is a ≈ 3.5 x 3 mm2, few-hundred-micron thick, freshly cleaved sample studied in an ambient air environment; the layers of the material are parallel to the exposed (001) surface. Bulk WTe2 is stable under such conditions. Although flakes may present a few-layer oxidation film over time, this is much thinner than the penetration depth of the beams in our experiment46,47,48. The sample crystallographic axes were pre-oriented using Fourier transform infrared (FT-IR) spectroscopy and verified in-situ by checking the angular settings required to observe the specific Bragg reflections49.
Time-resolved X-ray diffraction
The time-resolved X-ray diffraction experiment (Fig. 1a) was performed at the Bernina beamline at SwissFEL, Paul Scherrer Institute, in Villigen (Switzerland)17. The X-ray beam was generated by the FEL with a 50 Hz repetition rate and pulse duration shorter than 30 fs (rms).
The X-rays passed through a Si (111) double-crystal monochromator that selected X-rays at 8 keV photon energy with a bandwidth of 0.014%. A pair of Kirkpatrick-Baez mirror pair then focused the X-rays onto a spot with a highly elliptical 5 x 50 μm2 (FWHM) shape, such that the smaller dimension was vertical. The sample was then inserted at this location and aligned such that the incidence plane was horizontal, at a grazing angle of 0.7∘. This incidence angle was chosen to limit the X-ray penetration depth to match that of the exciting optical pump pulse. Owing to sample surface inhomogeneities we estimate a rather large ± 0.2∘ uncertainty in the X-ray incidence angle that may vary systematically with choice of reflection.
To excite the system, a near-infrared p-polarized laser pulse (800 nm), shorter than 35 fs (FWHM) and with a 100 Hz repetition rate, was employed and chopped to set the pump-probe scheme. It arrived at the sample with a 80∘ angle with respect to the surface normal with a 200 x 200 μm2 (FWHM) spot size, considering the section normal to the wavevector. The plane of incidence was the same as that of the X-rays, such as to minimize the angle between the two beams. This limits the loss in time resolution from geometrical factors to less than 35 fs while also suppressing reflection losses (see Supplementary Note 5). The fluences reported are the absorbed fluences using an estimate of the reflection of the material based on reported optical data48.
The jitter between the near-infrared and X-ray beams was corrected using a timing tool17. The Bragg conditions were obtained by rotating the sample along detector azimuthal angle ϕ. The diffracted X-ray beams were registered by a 1.5 Megapixels JUNGFRAU detector50, set 76 cm away from the sample. The diffracted intensities were then obtained by integrating the values registered by each pixel over a region of interest (ROI). A discussion about the fluence estimation can be found in Supplementary Note 5. The experiment was performed in ambient temperature and pressure conditions.
Time-resolved near-infrared reflectivity
To support the interpretation of the X-ray results, we performed time-resolved reflectivity measurements using a Ti:sapphire amplifier producing ≈50 fs and 800 nm pulses with a 250 kHz repetition rate. Divided by a beam splitter, part of the outcoming beam was directed in a 3-mm sapphire window to generate a supercontinuum of wavelengths between 550 and 1550 nm. The resulting light was directed to the sample to be used as a probe beam, together with the 800 nm pump, in a quasi-normal incidence configuration. The reflected beam was then filtered at 950 nm using a bandpass filter to acquire single-color measurements. The 800 nm pump beam and a 950 nm probe beam were linearly polarized along the y and x directions, respectively (see Supplementary Note 2). We measured the reflectivity signal as a function of the pump-probe delay and pump fluence conditions. The choice of the probe wavelength was made in order to observe significant contributions from at least the two most prominent modes (0.24 THz, shear mode, and 2.4 THz) based on previous results obtained on WTe2 by probing the coherent phonons effects with white light8. Here, these two phonons dominate the oscillatory response and thus we use a two-phonon empirical model to derive the associated parameters.
DFT simulations
To support our results, density functional theory (DFT) simulations were carried out using the QUANTUM ESPRESSO (QE)51 suite of codes. Pseudopotentials based on the projected augmented wave method (PAW)52 with the generalized gradient approximation (GGA) in the Perdew–Burke–Ernzerhof (PBE) parametrization for the exchange-correlation functional53 from the PSLIBRARY 1.0.054 were employed. The equilibrium configuration was obtained starting from an orthorhombic simulation cell with lattice constants a = 3.496 Å, b = 6.282 Å, and c = 14.073 Å crystallographic coordinates at room-temperature1. The electronic density and bandstructure were obtained using a 80 Rydberg plane wave kinetic energy cutoff and uniform 14 × 12 × 8 k-point mesh for integrations over the Brillouin zone under a fully relativistic description including spin–orbit coupling. The spin–orbit contribution is required to accurately reproduce the electronic structure around the Fermi level3. To obtain the zone-center phonon eigenvalues and eigenvectors, the dynamical matrix was calculated and diagonalized in a DFPT55 approach under the scalar relativistic approximation56 as implemented in QE; a kinetic energy cutoff of 50 Rydberg and a 8 × 6 × 4 k-point mesh were used. An additional characterization of the simulated system is presented in Supplementary Note 2.
Data availability
The data that support the findings of this study are available from the corresponding authors upon request.
References
Brown, B. E. The crystal structures of wte2 and high-temperature mote2. Acta Crystallogr. 20, 268–274 (1966).
Ali, M. N. et al. Large, non-saturating magnetoresistance in WTe2. Nature 514, 205 (2014).
Soluyanov, A. A. et al. Type-II Weyl semimetals. Nature 527, 495–498 (2015).
Wu, S. et al. Observation of the quantum spin hall effect up to 100 kelvin in a monolayer crystal. Science 359, 76–79 (2018).
Sharma, P. et al. A room-temperature ferroelectric semimetal. Sci. Adv. 5, eaax5080 (2019).
Dai, Y. M. et al. Ultrafast carrier dynamics in the large-magnetoresistance material wte2. Phys. Rev. B 92, 161104 (2015).
He, B. et al. Coherent optical phonon oscillation and possible electronic softening in wte2 crystals. Sci. Rep. 6, 30487 (2016).
Soranzio, D., Peressi, M., Cava, R. J., Parmigiani, F. & Cilento, F. Ultrafast broadband optical spectroscopy for quantifying subpicometric coherent atomic displacements in wte2. Phys. Rev. Res. 1, 032033 (2019).
Gu, L. L. et al. Optical-phonon-mediated photocurrent in terahertz quantum-well photodetectors. Appl. Phys. Lett. 106, 111107 (2015).
Sie, E. J. et al. An ultrafast symmetry switch in a Weyl semimetal. Nature 565, 61–66 (2019).
Amin, B., Kaloni, T. P. & Schwingenschlögl, U. Strain engineering of ws2, wse2, and wte2. RSC Adv. 4, 34561–34565 (2014).
Guan, M.-X., Wang, E., You, P.-W., Sun, J.-T. & Meng, S. Manipulating weyl quasiparticles by orbital-selective photoexcitation in wte2. Nat. Commun. 12, 1885 (2021).
Ji, S., Grøanäs, O. & Weissenrieder, J. Manipulation of stacking order in td-wte2 by ultrafast optical excitation. ACS Nano 15, 8826–8835 (2021).
Hein, P. et al. Mode-resolved reciprocal space mapping of electron-phonon interaction in the weyl semimetal candidate td-wte2. Nat. Commun. 11, 2613 (2020).
Sokolowski-Tinten, K. et al. Femtosecond X-ray measurement of coherent lattice vibrations near the lindemann stability limit. Nature 422, 287 (2003).
Johnson, S. L. et al. Nanoscale depth-resolved coherent femtosecond motion in laser-excited bismuth. Phys. Rev. Lett. 100, 155501 (2008).
Ingold, G. et al. Experimental station Bernina at SwissFEL: condensed matter physics on femtosecond time scales investigated by X-ray diffraction and spectroscopic methods. J. Synchrotron. Radiat. 26, 874–886 (2019).
He, P. et al. Nonlinear magnetotransport shaped by fermi surface topology and convexity. Nat. Commun. 10, 1290 (2019).
Ashcroft, N. & Mermin, N. Solid State Physics, chap. 21 (Saunders College, 1976).
Jha, R. et al. Anisotropy in the electronic transport properties of weyl semimetal wte2 single crystals. AIP Adv. 8, 101332 (2018).
Wang, Q. et al. Anomalous photothermoelectric transport due to anisotropic energy dispersion in wte2. Nano Lett. 19, 2647–2652 (2019).
Xu, N. et al. Evidence of a coulomb-interaction-induced lifshitz transition and robust hybrid weyl semimetal in Td − mote2. Phys. Rev. Lett. 121, 136401 (2018).
Kang, S.-H. et al. Reshaped weyl fermionic dispersions driven by coulomb interactions in mote2. Phys. Rev. B 105, 045143 (2022).
Di Sante, D. et al. Three-dimensional electronic structure of the type-ii weyl semimetal wte2. Phys. Rev. Lett. 119, 026403 (2017).
Ali, M. N. et al. Correlation of crystal quality and extreme magnetoresistance of wte2. Europhys. Lett. 110, 67002 (2015).
Lv, Y.-Y. et al. Dramatically decreased magnetoresistance in non-stoichiometric wte2 crystals. Sci. Rep. 6, 26903 (2016).
Kim, H.-J., Kang, S.-H., Hamada, I. & Son, Y.-W. Origins of the structural phase transitions in mote2 and wte2. Phys. Rev. B 95, 180101 (2017).
James, R. W. The optical principles of the diffraction of x-rays, The crystalline state - vol. II. (G. Bell & Sons, London, 1962).
Henke, B., Gullikson, E. & Davis, J. X-ray interactions: Photoabsorption, scattering, transmission, and reflection at e = 50-30,000 ev, z = 1-92. At. Data Nucl. Data Tables 54, 181 – 342 (1993).
Brown, P. J., Fox, A. G., Maslen, E. N., O’Keefe, M. A. & Willis, B. T. M. Intensity of Diffracted Intensities, vol. C, chap. 6.1 (International Union of Crystallography, 2006).
Garl, T. et al. Birth and decay of coherent optical phonons in femtosecond-laser-excited bismuth. Phys. Rev. B 78, 134302 (2008).
Jo, N. H., Wang, L.-L., Orth, P. P., Bud’ko, S. L. & Canfield, P. C. Magnetoelastoresistance in wte2: Exploring electronic structure and extremely large magnetoresistance under strain. Proc. Natl. Acad. Sci. USA 116, 25524–25529 (2019).
Lv, H. Y. et al. Perfect charge compensation in wte2 for the extraordinary magnetoresistance: From bulk to monolayer. Europhys. Lett. 110, 37004 (2015).
Pan, X.-C. et al. Carrier balance and linear magnetoresistance in type-II weyl semimetal wte2. Front. Phys. 12, 127203 (2017).
Zhu, Z. et al. Quantum oscillations, thermoelectric coefficients, and the fermi surface of semimetallic wte2. Phys. Rev. Lett. 114, 176601 (2015).
Wang, L. et al. Direct observation of a long-range field effect from gate tuning of nonlocal conductivity. Phys. Rev. Lett. 117, 176601 (2016).
Li, P. et al. Evidence for topological type-ii weyl semimetal wte2. Nat. Commun. 8, 2150 (2017).
Na, J. et al. Tuning the magnetoresistance of ultrathin wte2 sheets by electrostatic gating. Nanoscale 8, 18703–18709 (2016).
Wang, Y. et al. Direct evidence for charge compensation-induced large magnetoresistance in thin wte2. Nano Lett. 19, 3969–3975 (2019).
Zhang, X., Kakani, V., Woods, J. M., Cha, J. J. & Shi, X. Thickness dependence of magnetotransport properties of tungsten ditelluride. Phys. Rev. B 104, 165126 (2021).
Callanan, J. E., Hope, G., Weir, R. D. & Westrum, E. F. Thermodynamic properties of tungsten ditelluride (wte2) i. the preparation and lowtemperature heat capacity at temperatures from 6 k to 326 k. J. Chem. Thermodyn. 24, 627 – 638 (1992).
Liu, G., Liu, H., Zhou, J. & Wan, X. Temperature effect on lattice and electronic structures of wte2 from first-principles study. J. Appl. Phys. 121, 045104 (2017).
Ligges, M. et al. Observation of ultrafast lattice heating using time resolved electron diffraction. Appl. Phys. Lett. 94, 101910 (2009).
Pei, Y., LaLonde, A. D., Wang, H. & Snyder, G. J. Low effective mass leading to high thermoelectric performance. Energy Environ. Sci. 5, 7963–7969 (2012).
HQ graphene. http://www.hqgraphene.com/ (2022).
Lee, C.-H. et al. Tungsten ditelluride: a layered semimetal. Sci. Rep. 5, 10013 (2015).
Woods, J. M. et al. Suppression of magnetoresistance in thin wte2 flakes by surface oxidation. ACS Appl. Mater. Interfaces 9, 23175–23180 (2017).
Frenzel, A. J. et al. Anisotropic electrodynamics of type-ii weyl semimetal candidate wte2. Phys. Rev. B 95, 245140 (2017).
Schlepütz, C. M., Mariager, S. O., Pauli, S. A., Feidenhans’l, R. & Willmott, P. R. Angle calculations for a (2+3)-type diffractometer: focus on area detectors. J. Appl. Crystallogr. 44, 73–83 (2011).
Mozzanica, A. et al. The jungfrau detector for applications at synchrotron light sources and xfels. Synchrotron Radiat. News 31, 16–20 (2018).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Condens. Matter Phys. 21, 395502 (2009).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P. et al. Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 46, 6671–6687 (1992).
Dal Corso, A. Pseudopotentials periodic table: From H to Pu. Comput. Mater. Sci. 95, 337–350 (2014).
Baroni, S., de Gironcoli, S., Dal Corso, A. & Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515–562 (2001).
Takeda, T. The scalar relativistic approximation. Z. Phys. B 32, 43–48 (1978).
Kawamura, M. Fermisurfer: Fermi-surface viewer providing multiple representation schemes. Comput. Phys. Commun. 239, 197–203 (2019).
Kokalj, A. Xcrysden-a new program for displaying crystalline structures and electron densities. J. Mol. Graph. Model. 17, 176–179 (1999).
Acknowledgements
D.S. acknowledges support from the European Social Fund Operational Programme 2014/2020 of Region Friuli Venezia Giulia. High-performance computing resources were obtained from CINECA through the ISCRA initiative and the agreement with the University of Trieste and from Elettra Sincrotrone Trieste. V.O. acknowledges funding support from the Swiss National Science Foundation through Grant 200020_192337. E.A. acknowledges funding support from the Swiss National Science Foundation through Ambizione Grant PZ00P2_179691. M.P. acknowledges support from the Italian Ministry of University and Research (MIUR)—Progetti di ricerca di Rilevante Interesse Nazionale (PRIN 2017)—grant 2017KFY7XF. This work was supported by the NCCR Molecular Ultrafast Science and Technology (NCCR MUST), a research instrument of the Swiss National Science Foundation (SNSF). The research leading to these results received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 730872, project CALIPSOplus.
Author information
Authors and Affiliations
Contributions
The time-resolved X-ray experiment was performed by D.S., M. Savoini, F.C., L.B., J.D., V.O., S.H., E.A. and S.L.J. together with P.B., M. Sander, S.Z., Y.D., R.M., and H.T.L. who prepared and operated on the experimental endstation. The time-resolved optical reflectivity experiment was performed by D.S. under the supervision of F.C. The numerical simulations were performed by D.S. under the supervision of M.P. The experiment was conceived by F.P. and S.L.J. The manuscript was written by D.S., M. Savoini, and S.L.J.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Soranzio, D., Savoini, M., Beaud, P. et al. Strong modulation of carrier effective mass in WTe2 via coherent lattice manipulation. npj 2D Mater Appl 6, 71 (2022). https://doi.org/10.1038/s41699-022-00347-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-022-00347-z