Higher-indexed Moiré patterns and surface states of MoTe₂/graphene heterostructure grown by molecular beam epitaxy

Abstract

Stabilization of the 2H phase of MoTe₂ during molecular beam epitaxy (MBE) growth on graphene terminated 6H-SiC(0001) is highly desirable in order to take advantage of its promising properties in electronic applications. By properly adjusting the conditions, direct growth of the highly crystalline 2H phase of MoTe₂ has been achieved. In such van der Waals heterostructure, the atomically-clean interface between graphene and MoTe₂ permits the electronic coupling between the adjacent layers and the emergence of a high variety of Moiré patterns. In this paper, we investigate a single layer of 2H-MoTe₂ grown on graphene by MBE and we present scanning tunneling microscopy (STM) investigations combined with density functional theory (DFT) calculations and simulations of STM images. Our results show that the STM images of the MoTe₂/graphene heterostructure surprisingly amplify the otherwise weak Moiré potential modulations leading to the appearance of unique higher-indexed Moiré patterns. These patterns are unusually rich with many Fourier-overtones and show a remarkable variety of different applied bias voltages, revealing the complex electronic features of the heterostructure.

Introduction

In recent years, the progress of 2D materials growth and characterization has been significantly governed by the study of transition metal dichalcogenides (TMDs)¹. TMDs exhibit unique electrical and optical properties due to their tunable bandgap and the transition from an indirect bandgap in bulk to a direct bandgap in monolayer. Strong photoluminescence² and large exciton binding energy³ make them a promising candidate for a variety of optoelectronic devices, including solar cells⁴, photo-detectors⁵, light-emitting diodes⁶, and photo-transistors⁷. However, defect-free growth and detailed structural and electronic characterization of monolayer TMDs on desired substrates are still challenging.

Compared with other TMD materials, MoTe₂ possesses some distinct properties that make it attractive for research. Of the two phases (1T’ and 2H) that are stable at room temperature^8,9, the 2H phase displays a direct bandgap of ~1 eV, similar to that of Si, making it desirable for ambipolar field-effect transistors¹⁰. Many recent studies report on the growth of MoTe₂ on different substrates using various methods such as the Te flux controlled chemical vapor deposition (FCCVD)^11,12,13, chemical vapor transport (CVT)^14,15, chemical vapor deposition (CVD)^16,17,18, magnetron sputtering¹⁹, and molecular beam epitaxy (MBE)^20,21,22,23. MBE has proven the great advantages of precise growth control under highly reproducible conditions due to slow growth rates and the deposition in an ultra-high vacuum environment at lower growth temperatures⁹. The phase and the crystalline quality of MoTe₂ are also closely related to the choice of the suitable substrate. Graphene is recognized as one of the most promising ones for growing high-quality MoTe₂ because it is chemically inert with honeycomb structure, ideal for van der Waals (vdW) epitaxy and unstrained growth²¹. However, the practical production of the desired MoTe₂ phase encounters difficulties as a result of the very small formation energy difference between 2H and 1T’ phases in the films (~0.04 eV/MoTe₂)²⁴ and therefore requires very precise control of the growth conditions. In this context, we have previously reported MBE growth of MoTe₂ on graphene with the desired phase and good crystallinity^9,25. We have found that single-layer 2H-MoTe₂ films (referred to as 1H hereafter) grown on graphene induce the formation of Moiré patterns with various twist angles in a wide interval⁹. This phenomenon is also influenced by the synthesis conditions such as substrate temperature, beam flux, and post-growth annealing time^9,26.

Moiré pattern between 2D heterostructures²⁷ is very common as these systems are held together by vdW forces, which allow them to rotate relative to each other easily. These Moiré patterns have important consequences on the physical properties of the systems. A prime example is the particular electronic behavior of bilayer graphene with a small magic angle, which has opened a new area of research, the twistronics^28,29. As first described by Zeller et al. in detail^30,31 and later by ref. ³², Moiré patterns can be categorized according to the indices (mnpq) based on the reciprocal lattice vectors of the constituent layers (${\overrightarrow{G}}_{mn}$, ${\overrightarrow{G}}_{pq}^{\prime}$). Zeller et al. treated the frequency domain of the patterns transferring the problem of a Moiré lattice to the optical analog of a beat. In hexagonal systems, the most common Moiré pattern is the one with the lowest possible (mnpq) indices i.e., (1010) as commonly observed in several heterostructures such as graphene on graphene³³, graphene on hexagonal boron nitride (h-BN)³⁴, MoTe₂ on MoS₂³⁵ to name a few examples. Higher-indexed patterns typically have weaker potential modulation, and therefore their detection by scanning tunneling microscopy (STM) is limited. However, such higher-indexed patterns are expected to be observable around the twist angle of 30^∘36,37 because at such twist angles in hexagonal lattices, the wavelength of the dominant (1010) pattern becomes comparable to the atomic lattice, and therefore will no longer be observable, not masking anymore the higher-indexed patterns. The observation of the higher-indexed patterns is further complicated for commensurate heterostructures having finite supercells. In this case, the perfect atomic periodicity, i.e., the size of the supercell, can be larger than the Moiré periodicity, which appears beside the different Moiré patterns. While ref. ³² only treated the occurring frequencies of the pattern and left out the question of commensurability, Zeller et al. focused on this issue. In this context, the question arises whether or not patterns contain a quasiperiodic motif (introduced by ref. ³⁶) or a true commensurate unit cell.

In this paper, we show that unusual higher-indexed Moiré patterns together with the periodicity of commensurate supercells are observed by STM in the MoTe₂/graphene heterostructure around 30^∘ rotation angles. Moreover, we observe that these Moiré patterns depend strongly on the bias voltage. In heterostructures, some features of Moiré patterns can depend on the bias voltage. This can affect the amplitude of electronic corrugation³⁸, or even contrast inversion³⁹ can occur. However, here we report the unique drastic change of the Moiré periodicity with the bias voltage, indicating the presence of several higher-indexed patterns, amongst which one can selectively switch by changing the bias. This variability of the charge density is attributed to the competing contribution of Mo and Te orbitals for different bias voltages and to the strong influence of the graphene substrate, as revealed by our density functional theory (DFT) calculations. The presence of the higher-indexed Moiré makes the apparent patterns unusually rich and complex in the case of the MoTe₂/graphene heterostructure grown by MBE with high crystalline quality.

Results and discussion

STM of MoTe₂ on graphene

The experimental analyses of STM images before and after 2H-MoTe₂ grown on graphene are presented in Fig. 1.

Fig. 1: STM images of MoTe₂ formation on graphene over terminated 6H-SiC(0001) substrate.

a 500 × 500 nm² of bare graphene on terminated 6H-SiC(0001) substrate (V_Sample = +1 V, I_Tunnel = 800 pA) with an inset of the honeycomb structure, b After 2H-MoTe₂ formation taken on the same 500 × 500 nm² area (V_Sample = −0.6 V, I_Tunnel = 700 pA) with an inset of LEED pattern, and c 40 × 40 nm² of 1H-layer (V_Sample = +1 V, I_Tunnel = 5 pA), d–f Close-up observation of each Moiré pattern on local scan areas (I): $2\sqrt{3}$R30^∘, (II) $\sqrt{39}$R16.1^∘, and (III) $2\sqrt{7}$R19.1^∘ (in Wood's notation) taken on the black squares of corresponding regions as marked on the STM image (c), g Height profile of 2H layer taken along the black line of panel (b), h Schematic view of the STM tip-2H-MoTe₂ sample geometry where the distances on the figure are given as an illustration. G as marked on the STM images stands for graphene.

In Fig. 1a, a large STM image of 500 × 500 nm² with proper flat terraces of pristine graphene is shown together with an atomic resolution of the honeycomb structure in the inset, confirming the high crystalline quality of prepared graphene. After MoTe₂ formation (Fig. 1b), domains of a 2H structure are visible along with a small fraction of exposed graphene which can still be observed, labeled as “G” on the figure. The first layer of 2H-MoTe₂ (named 1H) covers most of the graphene surface. Small portions of a second layer (named 2H) form on the top of the first layer in the AB stacking order as evidenced by our previous study⁹. The LEED pattern (inset) shows a bright diffraction ring corresponding to the 2H phase. The additional diffraction spots originate from graphene and SiC substrate exclusively, which confirms that only the 2H-MoTe₂ phase was grown on graphene with high crystalline quality. The ring pattern is associated with a large number of micron-size crystallites of 2H-MoTe₂ with random in-plane orientations around a preferential orientation that is aligned with the graphene substrate. For further detailed information on single-phase stabilization, the tunneling current density of corresponding STM images together with RHEED and LEED (at low beam energy) patterns are also provided in Supplementary Fig. 1.

The height of the 2H layer is measured along the black line of Fig. 1b and shown in Fig. 1g. The average height between 1H and graphene (~4–6 Å) is lower than the height between 1H and 2H-MoTe₂ (~6–7 Å) from the measured height profile (see in Fig. 1h). The apparent height difference between the first and second layer of MoTe₂ is explained by the difference in the local density of states (LDOS) of the graphene and the MoTe₂ probed by the STM measurements at the applied bias voltage. Our DFT calculations proved that the lower LDOS on the domain of 1H-MoTe₂ requires the STM tip to move closer to the sample surface by ~2 Å to maintain the same tunneling current as on graphene support.

By zooming on 40 × 40 nm² of the 1H domain, three different periodic structures can be observed, marked as regions (I), (II), and (III) in Fig. 1c. Close-up imaging on the black squares of each region reveals Moiré patterns with surprisingly rich and complex inner textures shown in Fig. 1d–f. Figure 2 shows high-resolution STM images on a region at the interface between (I) and (III) using different sample biases. At the atomic scale, Moiré patterns can be clearly identified with supercells marked by black and green rhombuses on each region. As can already be seen here, these patterns are quite sensitive to the bias voltage. It is worth noting that previous STM studies show a dense triangular network of line defects in TMD samples grown by MBE, which are associated with mirror twin boundaries (MTBs)^{40,41,42,43,44}. However, those MTBs in the literature usually preserve their line format and do not show such a variation of the STM image with the bias voltage in sharp contrast with our Moiré patterns. Based on the periodicity of each supercell (~1.23 and ~1.85 nm respectively) in Fig. 2, this information along with theoretical lattice constants served as an input to a simple geometrical model to iterate through a large number of possible commensurate supercells as described in refs. ^45,46, finding the ones that match the experimental layouts. We kept here the lattice constant of the graphene substrate at a fixed value of 2.46 Å. Consequently, the possible commensurate structures are formed only at well-defined, discrete value pairs of the twist angle and MoTe₂ lattice parameter (see Supplementary Fig. 2). By utilizing commensuration conditions, we identified the superstructure in the region (I) as a $2\sqrt{3}\times 2\sqrt{3}$ arrangement, which has a twist angle of 30^∘, a Moiré angle of 30^∘, a supercell period of 1.23 nm, and a MoTe₂ lattice constant of 3.55 Å (hereafter $2\sqrt{3}$R30^∘ in Wood’s notation). In region (III), we found the supercell to display a different structure, namely $2\sqrt{7}\times 2\sqrt{7}$ with twist angle of 34.3^∘, a Moiré angle of 19.1^∘, a supercell period of 1.85 nm, and a MoTe₂ lattice constant of 3.51 Å (hereafter $2\sqrt{7}$R19.1^∘). As the lattice constant of MoTe₂ was reported previously to be 3.52 Å⁴⁷, our calculations show slight variations compared to this (~+0.8% and~−0.28%) in the different regions. Such a slight change in the lattice parameter (<1%) however is easily accommodated by van der Waals layers, as the commensuration can compensate for the excess elastic energy. We note that strain in this range (<1%) does not have a significant effect on the intrinsic electronic properties of MoTe₂. We also confirmed the resulting commensurate structures from the direct analysis of FFT images using the technique described in ref. ⁴⁸ (see Supplementary Fig. 3). The superlattice corresponding to the found commensurate structures and the MoTe₂ lattice line up remarkably well in the FFT images (see Supplementary Fig. 4), indicating indeed the commensurate nature of the Moiré domains.

Fig. 2: STM images of the same 10 × 10 nm² scan area taken at the interface between (I) and (III) shown in Fig. 1 c with different imaging conditions.

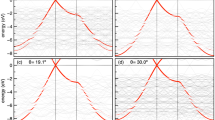
a 1 V/100 pA, b 0.5 V/100 pA, c 0.2 V/200 pA, d 2.0 V/20 pA, e 1.5 V/20 pA, f −0.5 V/100 pA. The twist angles (θ) between the graphene and the MoTe₂ lattices are 30^∘ and 34.3^∘ in the region (I) and (III). Supercells are marked by black and green hexagons in the two regions named as $2\sqrt{3}$R30^∘ and $2\sqrt{7}$R19.1^∘ in Wood's notation, respectively.

The two Moiré patterns are linked across a grain boundary between domains (I) and (III) as marked in Fig. 2a, which separates the two different surface structures, indicating that there are more than one crystallographic orientation formed in the 1H-MoTe₂ layer. As mentioned earlier, the LEED pattern suggests that these domains are randomly oriented. We emphasize here that the large size of the domain of the graphene grown on SiC almost excludes that this boundary is associated with the substrate. We extracted separate images of the two Moiré patterns corresponding to regions (I) and (III) from Fig. 2a, b, which are shown in Fig. 3. By applying fast Fourier transform (FFT) on these images (Fig. 3b, f for $2\sqrt{3}$R30^∘ and Fig. 3d, h for $2\sqrt{7}$R19.1^∘), further details about the Moiré patterns can be revealed. The Fourier components appearing as bright spots in the FFT can be directly matched to the supercell units marked with color vectors in the real space STM images. In order to precisely determine these components, we measured the FFT intensity by using the k-space profiles for the $2\sqrt{3}$R30^∘ and $2\sqrt{7}$ R19.1^∘ structures shown in Supplementary Fig. 5. We found that besides the periodic supercell of 1.23 and 1.85 nm, both Moiré patterns display an additional Fourier overtone corresponding to a periodicity of 0.7 nm. This component is a $\sqrt{3}$ overtone of the $2\sqrt{3}$ R30^∘ supercell and a $\sqrt{7}$ overtone of the $2\sqrt{7}$ R19.1^∘ supercell both having the same 2R0^∘ Wood’s notation. For the sake of clarity hereinafter these structures are referred to as 2R0^∘ and 2R’0^∘, respectively. With the help of Moiré theory, we will demonstrate later that these overtones incidentally coincide with the (2 × 2) lattice of the MoTe₂ in both cases. This is also evident in the FFT image of Fig. 3h, where the (2 × 2) peaks align perfectly with the (1 × 1) lattice (see also Supplementary Fig. 4, where we show in Fourier-space that the superlattice lines up very well with the MoTe₂ lattice, implying the commensurate property of the heterostructure). Moreover, the first (fundamental frequency) and second harmonics of the $2\sqrt{7}$R19.1^∘ are also visible. The observed FFT components illustrated with various hexagons are shown in Fig. 3i. The most fascinating aspect in this FFT analysis of our STM results is that the bias voltage influences dramatically the distribution of the Fourier intensities among the many Moiré overtones. For example in the case of the $2\sqrt{3}$R30^∘ structure, only the fundamental wavelength of 1.23 nm is observed at 1 V (Fig. 3f) while the second harmonic and $\sqrt{3}$ overtone become visible with higher intensity at a lower bias voltage of 0.5 V (Fig. 3b). It also occurs similarly in the $2\sqrt{7}$R19.1^∘ structure where the FFT intensity of the $\sqrt{3}$ overtone (Fig. 3d orange hexagon) appears very strong at 0.5 V besides the first and second harmonics, while the $\sqrt{7}$ overtone (Fig. 3h red hexagon) is prominent at 1 V rather than the $\sqrt{3}$ one. The appearance of different overtones and harmonics depending on the bias voltage makes the STM image of such Moiré patterns highly variable.

Fig. 3: Close-up STM images of the $2\sqrt{3}$R30^∘ (region (I)) and $2\sqrt{7}$R19.1^∘ (region (III)) Moiré structures and corresponding FFT images.

a–d taken on the same Fig. 2b while e–h taken on the same Fig. 2a; i The highlight of various Fourier components as illustrated by different color hexagons for both $2\sqrt{3}$R30^∘ and $2\sqrt{7}$R19.1^∘ Moiré patterns. θ marks the twist angle between the graphene and the MoTe₂ lattices.

The same analysis can be performed at the boundary of regions (II) and (III) as shown in Fig. 4a–c. Based on our STM images, we analyzed the Moiré structure in region (II) and we measured the Moiré periodicity to be about ~2.2 nm (Fig. 4d). Based on this, we identified the corresponding commensurate supercell (blue rhombus) to be a ($\sqrt{39}\times \sqrt{39}$) structure, having a twist angle of 33.1^∘, a Moiré angle of 16.1^∘, a 2.18 nm periodicity, and a MoTe₂ lattice parameter of 3.50 Å (hereafter $\sqrt{39}$R16.1^∘) (see also Supplementary Fig. 3c). The apparent morphology of the supercell in the STM image consists of two triangles with bright spots surrounding a void located at the center as circled (marked by dark blue circles). The distance along a side of the triangle is nearly three times the lattice constant of 1H-MoTe₂ and is illustrated in Fig. 4f. Model lattices of 1H-MoTe₂ and graphene are constructed with a twist angle of about 33.1^∘, showing a match with the STM image. More details of the observed Moiré pattern of $\sqrt{39}$R16.1^∘ are apparent in its corresponding FFT image in Fig. 4e. This pattern has an even richer Fourier spectrum compared to the previous ones. Not only the second (~1.1 nm) and third harmonics (~0.74 nm) of the fundamental frequencies of the supercell can be detected, but further Moiré overtones like $\sqrt{7}$ (~0.85 nm) and even a $\sqrt{13}$ (~0.63 nm) are visible. Indeed, we highlighted here such identified Fourier components of Fig. 4e in Fig. 4g with corresponding hexagons. Compared to Fig. 2, the similar behavior of the STM image taken on regions (II) and (III) with increasing the bias voltage (Fig. 4a–c) confirms the high variability of the measured real space Moiré patterns as a result of significant intensity changes in the Moiré overtones. Further details of FFT characterization for the Moiré patterns found in our system on other STM images are also provided in Supplementary Figs. 3, 4, 6, 7, 8.

Fig. 4: STM images of the same 10 × 10 nm² scan area taken at the interface between (II) and (III) shown in Fig. 1c using different sample biases.

a 1 V/100 pA, b 1.5 V/600 pA, c 2 V/5 pA; d Close-up STM image of the $\sqrt{39}$R16.1^∘ Moiré structure (region (II)) with the periodicity of ~2.2 nm with triangular shapes inside of the Moiré supercell (blue rhombus), and e corresponding FFT image taken on (d), f Model lattices of 1H-MoTe₂ within Moiré pattern $\sqrt{39}$R16.1^∘ on graphene (lattice constants of 0.246 nm for graphene and 0.352 nm for 1H-MoTe₂ and a twist angle θ of 33.1^∘), g schematic Fourier components illustrated with hexagons.

Moiré theory and DFT calculations of higher-indexed patterns

The Moiré patterns detected in our STM images have an unusually high degree of complexity compared to ones reported on other heterostructures in the literature. To reveal their nature, we analyzed the patterns in the context of Moiré theory found in refs. ^30,32. The possible Fourier components (${\overrightarrow{K}}_{mnpq}$) of the pattern are determined by the difference of the reciprocal lattices of the constituent layers, namely ${\overrightarrow{K}}_{mnpq}={\overrightarrow{G}}_{pq}^{\prime}-{\overrightarrow{G}}_{mn}$, where ${\overrightarrow{G}}_{mn}$ is a reciprocal lattice vector of the graphene and ${\overrightarrow{G}}_{pq}^{\prime}$ is a reciprocal lattice vector of the MoTe₂ lattice. During rotation of the layers whenever any ${\overrightarrow{G}}_{pq}^{\prime}$ and ${\overrightarrow{G}}_{mn}$ vectors get close to each other in reciprocal space, a Moiré pattern emerges in real space with a wavelength of ${\lambda }_{mnpq}=2\pi /| {\overrightarrow{K}}_{mnpq}|$. Based on this, we denote Moiré patterns with these four indices (mnpq), which define a unit cell vector in the k-space of this particular pattern. In this paper, we used an acute coordinate system, when defining the actual (mnpq) indices, so that the unit cell vectors of the atomic lattices form 60^∘ angle in reciprocal space (for details see Supplementary Fig. 9). In the case of simple geometrical lattices, the Moiré pattern, perceived by our eyes, arises from the lattices modulating the intensity of the visible light passing through them. In such an optical scenario, the larger the indices, the smaller the Fourier amplitudes following a heavily decreasing relationship³⁰. Such optical analogy turned out to be very well applicable to atomic lattices to describe the Fourier spectrum of Moiré patterns measured by STM³¹. On this basis, the most common Moiré pattern formed between hexagonal lattices is the one with the lowest possible (mnpq) indices i.e., (1010) with a maximum wavelength at 0^∘ twist angle, which was indeed found in the vast majority of cases^{39,49,50,51,52,53,54}, while patterns with higher indices were identified in a few occasions only (graphene/Ir(111)³⁶, graphene/Al(111)³⁷, and graphene/ReS₂⁵⁵). We assume that this is partly because their potential modulation is weak and therefore can not easily be detected by STM measurements.

In order to elaborate on higher-indexed Moire patterns in the context of the present study, we numerically calculated the λ_mnpq wavelength of some indices for the entire twist angle spectrum (θ = 0^∘ − 60^∘) of the MoTe₂/graphene heterostructure for a small range of MoTe₂ lattice parameters around the reported value of 3.52 Å (Fig. 5a). It is immediately noticeable that the wavelength of the (1010) pattern stays well below the experimentally measured Moiré periodicities of 1.23, 1.85, and 2.2 nm (see purple curves of Fig. 5a) and around 30^∘ its wavelength becomes comparable to the atomic lattice of the MoTe₂ surface layer. Then it will no longer be observable. The invisible (1010) pattern around 30^∘ provides an opportunity for other patterns to become observable as they do not overlap in real space with the dominant Moiré anymore. The (1110) pattern for example, with a wavelength peak at the twist angle of 30^∘ (see yellow curves of Fig. 5a) is the second visually most prominent pattern after (1010). Therefore, it immediately becomes visible to the eye in real space as we rotated a model of atomic lattices on top of each other to form the $2\sqrt{3}$R30^∘, $2\sqrt{7}$R19.1^∘, and $\sqrt{39}$R16.1^∘ superstructures (see red rhombus in Fig. 5b) and yellow rhombuses in Fig. 5c, d). The (1110) pattern apparent in Fig. 5b can be directly matched with the experimental Moiré pattern, in particular with the $2\sqrt{3}$R30^∘ structure previously shown in Fig. 3e both having the same 1.23 nm period. However, the further experimental values of 1.85 and 2.2 nm exceed the maximum wavelength of the (1110) pattern, indicating additional mechanisms to be revealed. Specifically, it can be shown that these larger periods equal the length of commensurate supercells of the $2\sqrt{7}$R19.1^∘ and $\sqrt{39}$R16.1^∘ structures. Commensuration in real space implies that a supercell can be defined besides the usual Moiré patterns. This supercell, in contrast to Moiré patterns in general, possesses perfect atomic periodicity, which happens only for particular discrete twist angles and lattice mismatches⁴⁵. In Fig. 5b–d, we displayed these commensurate supercells with red rhombuses.

Fig. 5: Analysis of the Moiré-wavelength and the identified MoTe₂/graphene commensurate superstructures near twist angle θ of 30^∘ between the hexagonal lattices.

a Calculated wavelength of differently indexed Moiré patterns in the twist angle range of θ = 0^∘−60^∘ with MoTe₂ lattice parameters 3.56 Å (lower curves) and 3.49 Å (upper curves). Blue stars represent the STM measured Moiré periods with the corresponding Wood's notations and twist angle values (θ) of the structures. b–d Model MoTe₂ and graphene lattices rotated above each other. Red rhombuses correspond to commensurate supercells of the Moiré domains experimentally identified in Figs. 2–4, yellow rhombuses correspond the λ₁₁₁₀ Moiré pattern. The relationship between the supercells (red rhombus) and the λ₁₁₁₀ pattern are the following: (1 × 1)λ₁₁₁₀ for $2\sqrt{3}$R30^∘, $(\sqrt{3}\times \sqrt{3}){\lambda }_{1110}$ for $2\sqrt{7}$R19.1^∘, and (2 × 2)λ₁₁₁₀ for $\sqrt{39}$R16.1^∘ structure.

As can be seen from these images, the supercells fit the (1110) pattern in different ways. In the case of $2\sqrt{3}$R30^∘, the supercell is equivalent to the (1110) Moiré: (1 × 1)λ₁₁₁₀ (see Fig. 5b), while for $2\sqrt{7}$R19.1^∘ we have $(\sqrt{3}\times \sqrt{3}){\lambda }_{1110}$ (see Fig. 5c) and a (2 × 2)λ₁₁₁₀ structure in the case of $\sqrt{39}$R16.1^∘ (see Fig. 5d). The supercells represent an extra modulation in the (1110) pattern that becomes visible on the STM images. Indeed, the Moiré beatings differ slightly on the atomic scale and only become perfectly identical with the period of the supercell in the (1110) pattern for the $2\sqrt{7}$R19.1^∘ and $\sqrt{39}$R16.1^∘ structures (corners of the red rhombuses in Fig. 5c, d). Only perfectly identical beatings will have the same STM contrast, therefore highlighting the supercell periods. The strong appearance of the supercell periods suggests that STM images of the MoTe₂/graphene system have a high sensitivity to the electronic properties in which the small atomic deviations of the Moiré stackings result in significant differences in the tunneling current. This will be further analysed in our DFT calculations below. Therefore, the (1110) pattern with the commensurate supercell periods displayed in Fig. 5b–d describe quantitatively the experimental patterns shown in Figs. 3e, g, 4d. Moreover, the commensurate supercells can be interpreted in Moiré theory as even higher-indexed Moiré patterns. To highlight this, we indicated the experimentally measured Moiré periods with blue stars in Fig. 5a. The measured Moiré periods sit very well on a calculated higher-indexed ${\lambda }_{313\overline{1}}$ curve, which has a maximum wavelength of 2.28 nm at θ = 33^∘ twist angle (see the red curve of Fig. 5a) supporting the higher-indexed origin of the experimental patterns.

The concept of the higher-indexed patterns and supercells is further verified by calculating the ${\overrightarrow{K}}_{mnpq}$ Moiré reciprocal vectors of the abovementioned commensurate supercells. We plotted them for each measured structure (Fig. 6a–c blue dots). In the figure, the smaller the indices of a ${\overrightarrow{K}}_{mnpq}$ component have, the bigger the blue dot we choose. It can be seen that the experimentally detected Fourier components in Figs. 3, 4 are fully reproduced by this method. We note that among the calculated Fourier components, the atomic lattice and the (1010) pattern (blue and dotted hexagons) are also highlighted, which are usually absent in the FFT images of the measurement. The fundamental frequencies correspond to the supercell periods of 1.23 nm (Fig. 6a), 1.85 nm (Fig. 6b), and 2.18 nm (Fig. 6c) are in perfect agreement with the experimentally measured periodicities. As can be seen, the dots depicting the fundamental frequencies are small compared to other points on the spectrum, which means that these patterns have high indices, namely the (313$\overline{1}$) mentioned earlier. The additional Moiré overtones detected in the measurements as patterns with smaller wavelengths (~0.7 nm) such as 2R0^∘ (θ = 30^∘) and 2R’0^∘ (θ = 34.3^∘) structures are also fully reproduced (see red hexagons in Fig. 6a, b), among the other experimental overtones of the $\sqrt{39}$R16.1^∘ structure (Fig. 6c). Figure 6a–c show the possible Fourier components of the investigated geometries with the corresponding Moiré indices in Fig. 6d. The complex electronic properties of the system define which Fourier component will be appeared in the STM image at different voltages among the many possible Moiré overtones. Based on the overtones, we found that the smaller Moiré periods such as 2R0^∘(θ = 30^∘) (detected under lower bias voltage in Fig. 3b) and 2R’0^∘ (θ = 34.3^∘) (detected at higher bias voltage in Fig. 3h) correspond to the (0211) higher indices (see red hexagons in Fig. 6d and the green theoretical λ₀₂₁₁ curve in Fig. 5a). Therefore, we conclude that the variation of the bias voltage transforms the Moiré pattern from (313$\overline{1}$) to (0211).

Fig. 6: Fourier components of the different Moiré structures.

a–c Calculated ${\overrightarrow{K}}_{mnpq}$ Moiré reciprocal vectors (blue dots) of the corresponding $2\sqrt{3}$R30^∘, $2\sqrt{7}$R19.1^∘, and $\sqrt{39}$R16.1^∘ superstructures (the bigger the blue dot the smaller the (mnpq) Moiré indices). d The colored hexagons and their Moiré indices (mnpq) shown in the image indicate the Fourier components that can be matched directly with the experimental FFT images from Figs. 3, 4, where the same color notation is used. The components of the (1 × 1) MoTe₂ lattice and the (1010) pattern are marked with blue and dotted hexagons in the images.

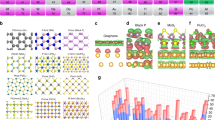
In order to investigate the connection between higher-indexed Moiré patterns and the electronic properties, we performed DFT electronic structure calculations taking into account the vdW interaction effects. For the calculations, we choose the 2$\sqrt{3}$R30^∘ geometry which has the smallest supercell size among the experimentally observed structures. The geometry relaxation revealed negligible corrugation effects, therefore both the graphene and the MoTe₂ layers remain flat at 30^∘ rotation angle similar to the case of the previously investigated MoS₂/graphene heterostructure⁵⁶. The absence of the atomic corrugation highlights the electronic structure origin of the observed Moiré patterns. The calculated total density of states (DOS) and also the sum of the partial DOS of the different atoms (C, Te, Mo) in the supercell are presented in Fig. 7a. The Fermi level is situated in the bandgap of the MoTe₂ (~1 eV), where no additional gap states are formed. We note that in the DFT calculations the Fermi level coincides with the Dirac point of the graphene (see Supplementary Fig. 10), while in the measurements the graphene is strongly n-doped (E_D ~ −0.4 eV) due to the SiC(0001) substrate (see Supplementary Fig. 11), rendering the Fermi level close to the conduction band minimum (CBM) of the MoTe₂. Therefore, substrate-induced doping should be considered when comparing the simulated and measured STM images at a given bias voltage.

Fig. 7: DFT electronic structure calculation and STM simulations for the $2\sqrt{3}$R30^∘ MoTe₂/graphene superstructure.

a Total density of states (DOS) and the sum of the partial DOS of the different atoms, Mo (blue), Te (green), C (red) in the supercell. Yellow lines mark the energy values of the maps shown in (c–e). b Relaxed geometry, where the red circles show the corner of the commensurate supercell and the blue square highlights the spatial area shown in (c–e) and in (f–h) upper panels. c–e Simulated dI/dV maps at z = 5 Å for +0.7, +1.0, +1.8 V, respectively. Each map is renormalized individually to its maximum. Maximum (minimum) values are 1.22 × 10⁻⁵ (9.26 × 10⁻⁶), 2.32 × 10⁻⁴ (2.26 × 10⁻⁴), and 1.27 × 10⁻³ (1.06 × 10⁻³) in 1/(ųV) units. f–h Simulated STM topography images calculated for V = +0.7, +1.0, and +1.8 V tip-bias voltages. Each map is renormalized individually to its maximum apparent height. Maximum (minimum) values are 6.23 (6.05), 6.14 (6.12), and 6.24 (6.22) in Å. Upper panels show the STM topography images in the spatial area used in (c–e), while lower panels are the same topography images in larger spatial dimensions. The distinct higher-indexed Moiré-patterns, such as the λ₁₁₁₀ (black rhombus in g, h) and the λ₀₂₁₁ (red and light-blue arrows in f, g) are explicitly apparent on the simulated STM images. A transition from λ₁₁₁₀ (1.23 nm) to λ₀₂₁₁ (0.7 nm) can be seen as the bias changes from +1.8 to +0.7 V, displaying a similar variable feature of the simulated patterns with the bias as detected in the experiments.

Figure 7c–e show the calculated dI/dV maps at z = 5 Å tip-sample distance for +0.7, +1.0, and +1.8 V bias values in the area marked in Fig. 7a. We found significant differences on these maps originating from the highly variable spatial distributions of the charge density due to the complex electronic structure of the system. The maximum dI/dV values at different bias voltages are located in some cases on the Mo atoms (V = 0.7 V), in other cases on the Te atoms (V = 1.0 V), and even they can be situated on the center of MoTe₂ hexagons (V = 1.8 V). However, we revealed that this property is intrinsic to the single-layer MoTe₂, irrespective of the graphene substrate. As can be seen from Fig. 7a, at +0.7 eV only Mo atoms have finite DOS values resulting in maxima on the Mo atoms in the corresponding simulated dI/dV map (Fig. 7c). By contrast, the Te atoms appear much brighter in the dI/dV map at +1.0 V (Fig. 7d), despite the fact that the Mo atoms still present higher DOS values. This means that the geometrical effect arising from the height difference of the Mo and Te atomic planes, i.e., the Te atoms are located at 1.8 Å higher than the Mo atoms, compensates for the larger Mo contribution to the DOS. We observed further contrast change at an increased bias value (+1.8 V), where the dI/dV maxima are localized at the center of the MoTe₂ hexagons (Fig. 7e). This spatial distribution originates from the increased weight of the in-plane p_x, p_y orbitals of Te and d_xz, d_yz orbitals of Mo atoms (see Supplementary Fig. 12). Besides the varying location of the dI/dV maximum with the bias voltage intrinsic to the MoTe₂ layer, the dI/dV values are further perturbed by the electronic interactions mediated between the graphene substrate and the MoTe₂ resulting that the same type of atoms are not equivalent inside the supercell. This is further illustrated by the inhomogeneous electronic density redistribution⁵⁷ resulting from the charge transfer between the graphene and MoTe₂ layers (see Supplementary Fig. 13). In detail, our DFT calculations indicate the accumulation of localized electrons on the bottom Te layer atoms while the depletion of delocalized electrons occurs from the graphene layer. This localized nature of the charge transfer causes spatial sensitivity because the relative positions between the carbon and Te atoms play a more important role. This sensitivity to small deviances in atomic positions is crucial for higher-indexed patterns to become visible in STM measurements. In accordance with this, it can be seen that even small changes in the local environment of the Mo and Te atoms in the supercell can result in significantly different dI/dV maxima along the corresponding Moiré periods, for example, those Te atoms have dI/dV maximum in Fig. 7d, which are situated on top of C-C bonds. This implies the important effect of the otherwise weak Moiré potential modulations. From the simulated dI/dV maps, we can conclude that the competing contributions to the DOS from the Mo and Te atoms together with the effect of the underlying graphene substrate lead to various patterns in the dI/dV maps at different bias voltages, explaining the sensitivity of the STM images in the measurements.

More importantly, simulated surface topographies (STM images) confirm the existence of higher-indexed patterns with different periodicities (see Fig. 7f–h). Due to substrate doping effects, the first dominant DOS peak of the CBM is situated at +0.2 V in the STS measurement. However, this DOS peak is located at +1 V in our DFT calculations, where the doping effect of the SiC substrate is neglected. Therefore, the +1.0 and +1.8 V bias voltages used in the simulated STM images (Fig. 7g, h) correspond to roughly +0.2 and +1.0 V in the experiments (Fig. 2c, a). We note, that this correspondence can only be approximate, due to the differences in the fine details between the theoretical and experimental band structures. For example, the SiC substrate doping is not rigidly shifting the bandstructure, as it is unevenly distributed between the layers of the heterostructure. From our DFT calculations, we found that the commensurate supercell dominates in the simulated STM image at a larger tip-bias voltage (+1.8 V) (Fig. 7h), where the center of the MoTe₂ hexagons at the supercell corners are visible. This pattern is equivalent to the λ₁₁₁₀ Moiré pattern with a 1.23 nm wavelength in perfect agreement with the experimentally observed periodicity in the measured STM image in Fig. 3e. For comparison, we have shown again side by side the measured and simulated STM images in Supplementary Fig. 12. At lower voltage (+1 V) in the simulation (Fig. 7g), second neighbor Te atoms appear as protrusions and their center as depression resulting in an additional 0.7 nm periodicity in the simulated STM image besides the supercell periodicity. This 0.7 nm periodicity is equal to the $\sqrt{3}$ overtone (λ₀₂₁₁), which is also detected in the measured STM image at the corresponding voltage in Fig. 2c. As the higher-indexed λ₀₂₁₁ tends to have a weaker potential modulation, it is more prone to be perturbed by weak substrate effects such as the presence of the SiC, which is neglected in our simulations. This may contribute to the small differences found between the simulated STM image and the measurements in this case. Nevertheless, our simulated STM images clearly show the change of the Fourier intensities and the appearance of different simultaneous Moiré periods with the bias voltage, while presenting a great variety of patterns, which we have already seen in the STM experiments.

Finally, based on our findings we address the question of the presence of higher-indexed Moiré patterns in other vdW heterostructures. As we have shown several conditions have to be fulfilled for the higher-indexed Moiré patterns to be visible in STM. Namely, (I) the twist angle between the hexagonal lattices should be around 30^∘, (II) the wavelength of higher-indexed Moiré patterns has to be in the measurable range (i.e., of the order of the nm), and (III) the weak potential modulations of the higher-indexed Moiré have to lead to changes of the electronic properties of the heterostructure with measurable STM fingerprints. Condition II constrains the lattice parameter of the constituent lattices. Based on these criteria higher-indexed Moiré patterns might have a chance to be observable in other heterostructures such as those based on graphene with other TMDs. Indeed, TMD lattice parameters are similar to MoTe₂ one (~3.1−3.5 Å), which makes the wavelength of higher-indexed Moiré patterns to be in the measurable range. Their electronic properties also show similarities including the orbital contributions of the transition metal and the chalcogen atoms. We note that the Moiré pattern observed on graphite/MoS₂ heterostructures around 27^∘ twist angle⁵⁸ is probably the signature of a higher-indexed Moiré. However, the main importance of the higher-indexed Moiré patterns lies in the fact that Moiré physics can also occur in many other heterostructures, which has not been considered previously in the field of twistronics. For example, recent measurements⁵⁹ show that higher-indexed Moiré patterns in graphene/xenon heterostructures effectively tailor the Dirac fermions, similar to the case of twisted bilayer graphene.

In conclusion, we investigated the formation of a variety of Moiré structures in 1H-MoTe₂ films on graphene terminated 6H-SiC(0001) under appropriate MBE growth conditions by STM. Three different patterns ($2\sqrt{3}$R30^∘, $\sqrt{39}$R16.1^∘, and $2\sqrt{7}$R19.1^∘) were observed using various tunneling conditions. They exhibit unusually rich and complex Moiré structures with the appearance of higher-indexed Moiré patterns predicted by Moiré theory. Additional Moiré overtones appeared in the measurements, which predominated in the pattern at certain voltages, making the electronic Moiré highly variable with the bias in the real space STM images. Our results also show a strong signature in the STM images of commensurate supercells around 30^∘, which are very faint in most heterostructures. DFT calculations and STM simulations have explained the complex Moiré patterns by revealing the importance of the electronic coupling between the layers in the MoTe₂/graphene heterostructure even for weaker Moiré potential modulations. Due to the important role that Moiré patterns already play in twistronics phenomena, we believe that higher-indexed patterns can further expand the possibilities of Moiré physics in the field of vdW heterostructures.

Methods

Sample preparation

In this study, graphene on n-type doped 6H-SiC(0001) was used as a substrate for the growth of MoTe₂ films. Following a vacuum graphitization process of 6H-SiC(0001) as detailed by ref. ⁶⁰, large-scale uniform double-layer graphene with the root mean square surface roughness of ~0.1–0.2 nm was obtained. The high crystalline quality of single-layer 2H-MoTe₂ films was formed on top of graphene by a multi-step MBE process as reported in our previous work⁹. After the 2H-MoTe₂ formation, a sample was taken out of the MBE chamber and preserved in a clean dry box filled with nitrogen gas from a pressurized nitrogen gas cylinder (≥99.9% pure) to avoid oxygen contamination as much as possible due to air exposure during transportation⁶¹.

STM characterization

Samples were transferred to low-temperature STM (Omicron) working at ~5 K and at a pressure lower than 1 × 10⁻¹¹ mbar. Before STM imaging, the sample was outgassed around ~250 ^∘C for 10 min to clean its surface. The STM topographic images were taken at constant current mode using an electro-chemically etched tungsten tip.

Computational details

Electronic structure calculations were performed in the framework of DFT implemented in the Vienna ab initio simulation package (VASP)⁶² using the plane-wave basis set and projector augmented wave method⁶³. The rev-vdW-DF2 functional was used to include properly the vdW interaction^64,65. The hexagonal supercell of the MoTe₂/graphene heterostructure ($2\sqrt{3}$R30^∘) has a supercell period of a = 12.23 Å and contains 24 Te, 12 Mo, and 50 C atoms, respectively. Atomic positions were relaxed using the conjugate-gradient method until the forces of the atoms were reduced to 0.01 eV/Å and the cut-off energy for the plane-wave basis set was chosen to be 500 eV. To avoid artificial interactions between periodic replicas of the MoTe₂/graphene layers, a vacuum interval of 18 Å was introduced in the z-direction. The Brillouin zone was sampled with (5 × 5 × 1) Monkhorst–Pack mesh⁶⁶ for geometry optimization, and (30 × 30 × 1) for density-of-states calculations. Simulated STM images were obtained by using the Tersoff-Hamann approximation⁶⁷ implemented as an s-type tip in the revised Chen method⁶⁸ in the BSKAN code^69,70.