Introduction

Friction exists in almost all mechanical systems with moving parts and it accounts for about a third of the world’s energy consumption1,2. Consequently, friction is the process of energy dissipation when the surfaces of moving parts slide against each other. The friction reduction is desirable at all scales from macro to nano for saving energy3,4. Atomically thin 2D materials such as graphene, transition metal dichalcogenides (e.g., MoS2), and boron nitride (h-BN) exhibit excellent lubrication properties and attract wide attention as solid lubricants in confined layers of molecular thickness for various micro-and nanoelectromechanical systems (MEMS/NEMS)5,6,7,8. Also, alternating hold and release the interfacial parts for steady operation in the control knob and sliding actuators of 2D materials-based MEMS/NEMS3 require controllable friction. It is necessary to not only seek the contributions but also the basic science such as energy dissipation to be understood to the friction on 2D materials effectively. The atomic force microscopy (AFM) methods have allowed basic studies of friction mechanisms on atomically thin 2D materials which intensively address how energy is dissipated at a sliding contact9.

There has been considerable progress in understanding the energy dissipation of friction on atomically thin 2D materials in the past few decades10. The structure11,12 and substrate13,14,15 affect the friction on atomically thin 2D materials deposited on the substrate due to the elastic deformation15, adhesion induced puckering16, and contact quality17,18. The kinetic energy associated with the AFM tip sliding on atomically thin 2D materials could attribute to dissipation by coupling the atomic relaxations to phonon modes that propagate away and the elastic deformation energy due to the out of plane deformation16,17,18. Then the defect generation and chemical functionalization of atomically thin 2D materials could tune the friction by increasing locally the potential corrugation and lowing the bending rigidity, but destroy the structure permanently19,20,21. The friction on the surface of atomically thin graphene is reduced dramatically by enhancing interfacial adhesion between graphene and supporting SiO2/Si substrate via plasma treatment of the substrate to suppress the puckering effect16,22. However, the tuning of the friction on atomically thin graphene is irreversible because the interfacial bonding is hard to recover to the initial state23. The friction on monolayer graphene can be modulated reversibly by tuning the atomic-level contact quality with simple mechanical straining under the relatively small range of applied load18. In a word, the energy dissipation of friction on atomically thin 2D materials is still undefined for controllable tuning.

The sliding AFM tip during friction involves the direct transfer of energy into the phononic dissipation and electron-hole pairs before transfer to the phonon populations. The electron-phonon coupling (EPC) becomes another channel for energy dissipation and builds a link between electronic and phononic effects12. Consequently, the energy of friction can be dissipated through phononic consumption and electronic contribution24,25,26. Electronic contributions to energy dissipation of friction on atomically thin 2D materials need to be manifested in many physical phenomena. Dong27 quantitatively calculated the effect of EPC on the friction of monolayer graphene by MD simulation with a Langevin equation and found the friction increases slightly with the increase of EPC. Filleter et al.12 found that the nanofriction on monolayer graphene was twice than that on bilayer graphene due to the strong EPC in monolayer graphene by means of angle-resolved photoemission spectroscopy. While a deep understanding of the EPC affects the frictional properties of 2D materials in essence is still required. Park et al.28 discovered that the accumulation of carriers near the semiconducting surface leads to excess friction due to high carrier density. Furthermore, the electron doping for single-layer and bilayer graphene transistors has been investigated with non-destructive Raman spectroscopy characterization based on the renormalization of the G and 2D modes as a function of carrier concentration29. However, the electronic contribution to friction during sliding contacts provides a possible method to tune the friction on atomically thin 2D materials through the carrier concentration30.

The semiconductor materials offer an interesting platform to investigate the electronic contribution to energy dissipation where energy dissipation is linked to interaction with the electron system. The charge carrier concentration and energy band alignment of semiconductors could be extensively and precisely controlled by the electric field31. In contrast to the zero gaps of graphene and wide gap of boron nitride32, mechanically exfoliated atomically thin MoS2 exhibits unique n-type semiconducting properties and tunable bandgap33. The carrier concentration in atomically thin MoS2 can be modulated easily with high sensitivity in a relatively large range from ~1013 to 1015 cm−2 by many orders of magnitude using the gate voltage34,35. Atomically thin MoS2 with semiconductive properties provides the possibility to study the effect of free charge carriers in the energy dissipation of friction because it is possible to reversibly change their density over many orders of magnitude. Scanning Kelvin force microscopy (SKPM) has been used to measure the contact potential difference (CPD) of atomically thin MoS2 under the gate voltage to calculate the variation of carrier concentration during the carrier accumulation and depletion36,37. The strengthening degree of EPC on atomically thin MoS2 could be detected by the Raman spectra. As the degree of EPC correlated strongly with carrier concentration, the potential distribution of atomically thin MoS2 provides the connection of carrier concentration with energy dissipation based on the modulation of gate voltage38. Then, the friction on atomically thin MoS2 could be tuned by regulation of the carrier concentration over many orders of magnitude based on field effect.

In this manuscript, the carrier concentration of atomically thin MoS2 deposited on SiO2/Si substrate is controlled by gate voltage (Vg) based on field effect. Then the electronic friction and energy dissipation on atomically thin MoS2 are investigated by modulating the degree of EPC with varying carrier concentration based on atomic-scale stick-slip calculation, surface potential, and in-situ Raman spectroscopy under the external electric field. The friction on atomically thin MoS2 is tuned dynamically, repeatably, and controllably based on the modulation of the carrier concentration further.

Results and discussion

Friction properties under the electric field

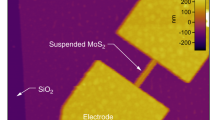
The topography of the atomically thin MoS2 on SiO2/Si substrate acquired by AFM in tapping mode is shown in Fig. 1b. The height of atomically thin MoS2 is about 0.9 nm corresponding to a single layer from the topography profile in the inset of Fig. 1b. Then, the nanofriction of atomically thin MoS2 deposited on SiO2/Si substrate was investigated using calibrated AFM under the gate voltage, as schematically shown in Fig. 1a. As shown in Fig. 1c, the Vg was sequentially applied in the order of 0–−5 V and then return to 0 V. The nanofriction on atomically thin MoS2 decreases at Vg = −5 V and then recovered fully to its initial state when Vg was returned to 0 V. The nanofriction has little change under relatively low negative Vg < −5 V (Supplementary Information Fig. 1). The nanofriction on atomically thin MoS2 at Vg = −5 V decreases about 20% contrast to the initial value from Fig. 1c. The nanofriction on atomically thin MoS2 is reduced obviously at the negative gate voltage of −5 V and decreases slightly with the increase of the negative bias when the gate voltage is beyond −5 V. However, the nanofriction on atomically thin MoS2 under the Vg = 5 V increases almost to 1.8 times than the initial value, as shown in Fig. 1d. The nanofriction on atomically thin MoS2 increases with the increase of positive gate voltage from 0 to 5 V, then recovered fully to its initial value when Vg was returned to 0 V, as shown in Fig. 1d. Therefore, the nanofriction on atomically thin MoS2 can be reversibly tuned by the regulation of Vg. Also, the polarity of the applied Vg exhibits a different effect on the nanofriction of atomically thin MoS2. Figure 1e shows the curves of nanofriction on atomically thin MoS2 versus the applied load measured under different Vg. Figure 1f shows the nanofriction on atomically thin MoS2 at a constant load of 10 nN under different Vg. The corresponding relationship between the magnitude of nanofriction and the applied Vg is shown in Fig. 1g. The high-resolution AFM image of atomically thin MoS2 denotes that it can remain stable after the friction test under the external electric field (Supplementary Information Fig. 2). It can be clearly seen that the nanofriction on atomically thin MoS2 was affected by the direction and magnitude of the Vg.

Fig. 1: The nanofriction experiments under different Vg.
figure 1

a Schematic of the nanofriction measurements on atomically thin MoS2 under different Vg. b AFM image and optical image(inset) of atomically thin MoS2 including the height profile of atomically thin MoS2 along the red dash line(inset). Scale bar: 2 μm. c Friction map with the applied load of 10 nN under the modulation of Vg from 0 V to −5 V and back to 0 V. The inset shows the profiles of the nanofriction indicated by the white arrow line. Scale bar: 100 nm. d Friction map with the applied load of 10 nN under the modulation of Vg from 0 V to 5 V, then back to 0 V. The inset shows the profiles of the nanofriction indicated by the white arrow line. Scale bar: 100 nm. e The nanofriction on atomically thin MoS2 as a function of applied load with different Vg. f The nanofriction at a constant load of 10 nN under different Vg. g The nanofriction on atomically thin MoS2 varied with the different Vg. Error bars represent standard deviations.

Full size image

Mechanism

The adhesion on atomically thin MoS2 were measured using AFM under different Vg. Figure 2a shows the adhesive force on atomically thin MoS2 and electrostatic force as a function of the Vg. The adhesion Fad approximately follows a parabolic law, i.e., Fad ∝ V 2, with little difference between positive and negative Vg. The Fad mainly consists of van der Waals force (FvdW), electrostatic force (Fele), capillary force (Fcap), and chemical bonding force (Fchem) in an ambient environment, which can be written as:

$$F_{{{{\mathrm{ad}}}}} = F_{{{{\mathrm{vdW}}}}} + F_{{{{\mathrm{ele}}}}} + F_{{{{\mathrm{cap}}}}} + F_{{{{\mathrm{chem}}}}}$$
(1)
Fig. 2: Force-distance curves on atomically thin MoS2 and variation of contact area under different Vg.
figure 2

a Adhesion and electrostatic force as a function of Vg. b Typical force-distance curves measured under the positive Vg. c Typical force-distance curves measured under the negative Vg. d Plots of the friction force versus the applied load on atomically thin MoS2 at Vg = 0 V. e The nanofriction caused by electrostatic force (fele) and additional effect (fextra). f Variation of the true contact area during AFM tip sliding on atomically thin MoS2 under different Vg. Error bars represent standard deviations.

Full size image

The surface properties of mechanically exfoliated atomically thin MoS2 keep highly hydrophobic and stable with barely dangling bonds under different Vg (Supplementary Information Fig. 3). Also, any effect of a changing tip structure, geometrically or chemically can be neglected during the nanofriction experiment under different Vg. The change of FvdW, Fcap, and Fchem can be neglected for the increase of the adhesion between the AFM tip and atomically thin MoS2 under different Vg. Consequently, the main reason for the change of adhesion force is the effect of Fele under different Vg. The electrostatic force caused by the electric field could be quantitatively calculated from the adhesion measurement of the single force curve under different Vg. So the Fele can be calculated using Eq. (1) at different Vg, as shown in Fig. 2a. Based on the quadratic fit of the electrostatic force, the relationship between the Fele and the Vg is

$$F_{{{{\mathrm{ele}}}}} = 0.14(V_{{{\mathrm{g}}}} - 0.64)^2 + 0.07$$
(2)

The electrostatic forces at Vg = 0 V, 5 V, 10 V, −5 V and −10 V are about 0 nN, 2.73 nN, 12.4 nN, 4.69 nN and 15.92 nN, respectively. The electrostatic force would increase the interaction between the tip and the atomically thin MoS2 and create additional friction. Therefore, the additional nanofriction (fele) caused by Fele was calculated while the Fele was treated as an additional load to the AFM tip. The typical single force curves on the atomically thin MoS2 were acquired with the AFM tip under the positive Vg, as shown in Fig. 2b. The difference of pull-off force between 0V and 6 V reveals the attraction contact because of the electrostatic interaction. The typical single force curves on the atomically thin MoS2 under the negative Vg shown in Fig. 2c have a similar tendency as the positive Vg.

The initial value of nanofriction starts with the adhesion force of 7.8 nN and the corresponding normal load is also 7.8 nN. Therefore, fele can be given by

$$f_{{{{\mathrm{ele}}}}} = \mu \times F_{{{{\mathrm{ele}}}}}$$
(3)

where μ is defined as the equal friction coefficient fitted from the friction as a function of load, as shown in Fig. 2d. The values of fele were calculated approximately to be 0 nN, 0.11 nN, 0.50 nN, 0.19 nN, and 0.64 nN at the Vg of 0 V, 5 V, 10 V, −5 V, and −10 V, respectively. Consequently, the increases of the nanofriction under different Vg are far more than the additional fele caused by electrostatic force. It can be concluded that there is an additional effect leading to the nanofriction increasing. Therefore, the nanofriction (fextra) caused by the additional action can be given by the equation:

$$f_{{{{\mathrm{extra}}}}} = f_{{{\mathrm{g}}}} - f_{{{{\mathrm{ele}}}}} - f_0$$
(4)

where f0 is the nanofriction at Vg = 0 V, fg is the nanofriction force under the different Vg with the applied load of 7.8 nN. The force of electrostatic attraction was supposed to increase the adhesion force, then increase nanofriction under the normal electric field. Figure 2e also shows that the electrostatic force is insufficient to increase the nanofriction to such an extent. Consequently, there is an additional mechanism for the increase on the nanofriction but the load. Considering that the change of adhesion force is closely related to the change of contact area, the nanofriction usually agrees well with the true contact area based on the contact model of Derjaguin-Müller-Toporov (DMT). As shown in Fig. 2f, the changes of contact area between the AFM tip and atomically thin MoS2 (Detailed calculation process in Supplementary Information Fig. 4) could not account for the obvious variation in nanofriction under different Vg. These findings indicate that the fele plays a small role in the change of nanofriction on atomically thin MoS2 under the different Vg. Meanwhile, the gate voltage induced another factor to change the nanofriction on atomically thin MoS2 besides the contact area.

The atomic-scale stick-slip behaviors on atomically thin MoS2 were measured using AFM to comprehend the underlying mechanism under different Vg further. The lateral force curves at atomic scale under different Vg are shown in Fig. 3a. The sawtooth shape of the trace shows the atomic lattice period of about 0.31 nm corresponding to the lattice constant of atomically thin MoS2. It is also clearly observed that the distance of the stick-slip period increases from 0.31 nm to 0.87 nm when the Vg was regulated from 0 V to 4 V. The atomic-level stick-slip behaviors of the lateral force on atomically thin MoS2 change with Vg, then return to the original. As the Vg increased, the stick-slip behaviors switch from single-slip to multiple-slip regime. The multiple-slip regime can also be fully recovered to a single-slip regime when Vg returns from 4 V to 0 V, as shown in Fig. 3a. The reversible transition between single slip and multiple slips indicates that the atomic-scale stick-slip behaviors can be reversibly modulated by the Vg. The lateral force map in the sliding process under different Vg is shown in Fig. 3b. Figure 3b was used to analyze the lateral force map in the sliding process under different gate voltages. Figure 3b indicated that the multiple-slip regime can also be fully recovered to a single-slip regime when Vg changes from 0 V to 6 V and then return to 0 V. Few regular atomic stick-slip motions are also observed when Vg ≥ 6 V (Supplementary Information Fig. 5). As shown in Fig. 3c, the mean lateral force increases with the increase of Vg. In the meantime, the total energy dissipation calculated from the atomic-scale stick-slip curves increased monotonically with the increase of the positive Vg shown in Fig. 3c. In addition, the distance between the trace and retrace values decreases demonstrating less energy dissipation for the decrease of average nanofriction under the negative Vg.

Fig. 3: Atomic-scale friction and stick-slip behavior on atomically thin MoS2 under different Vg.
figure 3

a Stick-slip behavior measured at Vg = −4–+4 V, respectively. b Lateral force mapping under different Vg: the gate bias voltage was dynamically modulated from 0 V to 6 V and return to 0 V. Scale bar: 1 nm. c Energy dissipation and lateral peak force under different Vg. d The lateral contact stiffness k under different Vg. Error bars represent standard deviations.

Full size image

The increase in the lateral force of stick-slip asymmetry suggests an incremental energy corrugation (see Supplementary Information Fig. 6)39. Therefore, a large lateral force is required to cross the barrier resulting in more energy dissipation under the positive Vg. The lateral contact stiffness was extracted from the slope of each stick phase in lateral force curves at the atomic scale in Fig. 3a. It has been reported that the value of lateral contact stiffness increases with load, indicating the increase of the contact area40. However, Fig. 3d shows that the lateral contact stiffness is almost kept stable under different Vg at a given load. Generally, the lateral contact stiffness would show a prominent deviation by the sliding energy barrier41. In addition, the average shear stress of the contact was analyzed. The friction (F) is proportional to the real contact area (A) as F = τ × A41, where τ is the shear strength. The real contact area under different gate voltages has been obtained based on the DMT model shown in Fig. 2f. The variation of the contact area and shear strength with gate voltages is shown in Supplementary Fig. 7 (see Supplementary Information). The shear strength increases under the positive gate voltages and decreases under the negative gate voltages. However, the data in Fig. 3 shows that the contact stiffness remains unchanged under different bias voltages. The reason is that Formula (1) holds if electronic contributions to friction are not involved28. These results indicated that the shear stress is hard to explain the experimental results of MoS2 under the electric field. Consequently, the variation of nanofriction on atomically thin MoS2 at different Vg can attribute to another factor beyond the energy dissipation from the energy barrier.

In addition to the changes in electrostatic force between the tip and atomically thin MoS2 under the external electric field, a more trivial effect of the Vg is to modulate the carrier concentration based on the electric field effect42. The carrier concentration can be calculated based on \(n = {{{\mathrm{N}}}}_{{{\mathrm{c}}}}{{{\mathrm{exp}}}}\left( {\frac{{ - \left( {E_{{{\mathrm{C}}}} - E_{{{\mathrm{F}}}}} \right)}}{{{{{\mathrm{K}}}}_{{{\mathrm{B}}}}{{{\mathrm{T}}}}}}} \right)\)43,44, where Nc = (2m*)/(πħ2) = 3.8 × 1014eV cm−2 is the density of states in the conduction band, EC is the bottom of the conduction band, KB is Boltzmann constant (KB = 1.380649 × 10−23 J/K), T is the temperature (300 K). EF is the Fermi energy level. EF can be calculated by measuring the surface potential through SKPM. Therefore, the SKPM test is used to calculate the carrier concentration of MoS2. The work function of MoS2 can be calculated by SKPM based on the formula of ΔCPD = (Wtip − Wsample)/e45, where Wsample and Wtip are the work functions of the MoS2 and tip, e is the electronic charge. The work function of MoS2 can be calculated by measuring ΔCPD with SKPM, and then the Fermi energy level of MoS2 can be calculated by W = 0−EF. However, the surface potential of MoS2 is not only determined by the work function of MoS2 but also directly affected by the electric field after applying the gate voltage. The surface potential of SiO2 under the different Vg was measured and the results are shown in Supplementary Fig. 8 (Supplementary Information). To minimize the influence of the applied electric field on the SKPM test, the surface potential of SiO2 was used as the reference. Because the relationship between the surface potential of SiO2 and gate voltage is linear. The surface potential of SiO2 is consistent with the Vg indicating that the work function of SiO2 as an insulator is very little affected by the Vg. Therefore, the surface potential difference between SiO2 and MoS2 (ΔCPD) was used to reflect the effect of electric field on MoS2, which is relatively more accurate. The surface potential of MoS2 deposited on SiO2/Si substrate under different Vg was shown in Fig. 4a–l. The yellow dotted box denotes the area of the atomically thin MoS2 on the surrounding SiO2/Si substrate. The surface potential of atomically thin MoS2 increases with the increase of positive Vg as presented in Fig. 4a–f. Also, the surface potential of atomically thin MoS2 decreases with a decrease of the negative Vg, as shown in Fig. 4h–l. The potential of MoS2 is lower than the potential of SiO2 under the positive gate voltages indicating that the MoS2 is an n-type semiconductor, while the potential of MoS2 is higher than the potential of SiO2 under the negative gate voltages indicating that the n region is reverse-biased causing depletion or weak inversion36. Surface potential profiles along the atomically thin MoS2 on the SiO2/Si substrate under the different Vg are shown in Fig. 4m. The values of ΔCPD are given in Fig. 4n after applied gate voltage from −6 to +6 V. Therefore, the carrier concentration was calculated based on \(n = {{{\mathrm{N}}}}_{{{\mathrm{c}}}}{{{\mathrm{exp}}}}\left( {\frac{{ - \left( {E_{{{\mathrm{C}}}} - E_{{{\mathrm{F}}}}} \right)}}{{{{{\mathrm{K}}}}_{{{\mathrm{B}}}}{{{\mathrm{T}}}}}}} \right)\), where EC = −3.9246, KBT = 0.0259 eV47, EF = −Wsample. The work function of conductive tip is 4.29 eV. The ΔCPD is 0.043 V at the gate voltage of 0V and the corresponding Fermi energy level is EF = −4.22. The ΔCPD is 0.102 V at the gate voltage of 5 V and the corresponding Fermi energy level is EF = −4.13. Therefore, the carrier concentration of MoS2 is 3.4 × 109 cm−2 at the gate voltage of 0 V (intrinsic carrier concentration) and 0.12 × 1012 cm−2 at the gate voltage of 5 V. Carrier concentration n can also be approximatively calculated using the idealized parallel-plate capacitor model with \(n = C_{{{{\mathrm{SiO}}}}_2} \times V_g\) (\(C_{{{{\mathrm{SiO}}}}_2}\) is ~15 nF cm−2 for 300 nm SiO2 dielectrics)48. Therefore, the alternate surface potential of atomically thin MoS2 suggests that the carriers accumulate under the positive Vg and dissipate under the negative Vg from the surface potential characterization and calculation.

Fig. 4: Surface potential mapping of atomically thin MoS2 on SiO2/Si substrate.
figure 4

a–l The surface potential mapping of atomically thin MoS2 under different Vg: −6–+6 V. Scale bar: 2 μm. m The line profiles of surface potential along the white line across the atomically thin MoS2 under different Vg. n ΔCPD of atomically thin MoS2 as a function of Vg. Error bars represent standard deviations.

Full size image

The variation of the CPD also indicates the direction and amount of energy band bending and the position of the Fermi level at the surface caused by surface electron states49. Since the atomically thin MoS2 is n-type semiconductor, the Fermi level in equilibrium is close to the conduction band (CB), as shown in Fig. 5a. The energy band bends downward and Fermi level is closer to the conduction band under the positive Vg. When a positive Vg is applied, only a few tenths of electron-volts shift at the conduction band edge50. This effect is clearly observed in Fig. 4n, where a positive Vg results in a little increase of △CPD due to its proximity to CB. However, the change of Fermi level under the negative is significantly changed due to the large distance between the Fermi level and the valence band (VB), as shown in Fig. 5c. Therefore, a large increase in ΔCPD was observed under the negative Vg. Furthermore, the variation in carrier concentration contributes to the shift of the position of Fermi level by the band bending. The energy band of atomically thin MoS2 bends downward and the Fermi level is closer to the conduction band resulting in carrier accumulation under a positive Vg. Figure 5c shows that the energy band bends upward and the Fermi level is closer to the valence band under the negative Vg, indicating that the carrier dissipates near the atomically thin MoS2 surface.

Fig. 5: Energy band diagram of atomically thin MoS2 with n-type semiconductor properties.
figure 5

a Energy band diagrams of atomically thin MoS2 at equilibrium. b The energy band bending and electron accumulation caused by the existence of donor-like surface states under the positive gate voltage. The band diagram of the MoS2/SiO2/Si structure. c The band diagram of the MoS2/SiO2/Si structure at negative gate voltage. The energy band bending and surface electron depletion under the negative gate voltage.

Full size image

Although the surface potential decreases significantly under the negative Vg, the corresponding carrier concentration decreases slightly. Similarly, the friction (or peak force) in Fig. 3c also shows a slight decrease as the voltage increases from 0 V to −4 V. Therefore, the decrease of ΔCPD in Fig. 4n indicates that the carrier concentration decreases under the negative gate voltage. Therefore, the decrease of carrier concentration under the negative Vg may be closely related to the decrease of nanofriction.

The nondestructive characterization of in-situ Raman spectroscopy was explored to investigate the effect of carrier concentration on the EPC on atomically thin MoS2 under different Vg. The schematic diagram of Raman spectroscopy analysis on the gate-modulated carrier concentration of atomically thin MoS2 was depicted in Fig. 6a. Figure 6b displays the evolution of zone-center phonon E12g and A1g modes of the atomically thin MoS2 under different Vg. As depicted in the inset of Fig. 6b, the A1g phonon involves the sulfur atomic vibration in the opposite direction along the c axis (perpendicular to the basal plane), whereas the E12g mode illustrates the displacement of Mo and S atoms are in the basal plane. The dependence of the change in different renormalization mode frequencies of the two modes A1g and E12g on the carrier concentration from the obtained Line-shape parameters show that the A1g mode frequency softens by 4 cm−1, as compared to only ~0.6 cm−1 for the E12g mode under the maximum voltage of 20 V. The linewidth of the A1g mode increases significantly by ~0.98 cm−1 for the maximum doping achieved, whereas the linewidth of the E12g mode does not show appreciable change. The renormalization A1g mode could be used as a sign of the quantitative EPC corresponding to the carrier concentration modulated by the Vg. The down-shift of A1g mode is due to the increase of carrier concentration leading to the occupation of an anti-bonding state in the conduction band of atomically thin MoS2. The occupation of an anti-bonding state increases the total electron energy of the system and weakens the Mo-S bond due to electron doping. Therefore, electron doping caused a significant change in the EPC of the A1g mode, while the E12g mode of Raman spectra with symmetry is quite insensitive to the external electric field. The phonon frequency and linewidth of the E12g mode are much less dependent on carrier concentration. Figure 6c, d show the shift of the mode frequencies and the corresponding full width at half maximum (FWHM) as a function of Vg, respectively. The A1g mode specifically exhibits a strong sensitivity to electron doping and the phonon frequency decreases by 4 cm−1 and the linewidth broadens by 1.1 cm−1 for electron doping at the Vg of 20 V. The FWHM of Raman mode derives from three factors as given below: ΓFWHM = Γ0 + Γanh + ΓEPC, where Γ0 is the intrinsic FWHM, Γanh denotes the phonon-phonon interaction, and ΓEPC is due to EPC51. Therefore, the ΓEPC can be used to illustrate the strength degree of EPC. The Γ0 and Γanh are expected to be the same at different Vg. The FWHM of A1g mode increases with the increase of carrier concentration. However, the FWHM of the E12g phonon was independent of the electron concentration38. The high level of carrier concentration causes the strong strength of EPC from the change in the A1g. The ΓEPC increases with the increased carrier concentration indicating that the strength of EPC increases with the increased carrier concentration. The friction increases with the increase of the carrier concentration, indicating that the energy dissipation of friction is consistent with the strengthening of EPC. Both the friction and carrier concentration increase with the increase of gate voltage confirming a strong correlation between the friction and carrier concentration from Fig. 6e. The data of friction and carrier concentration were fitted to quantify the relationship between the friction and carrier concentration. The fitted curve in Fig. 6f shows that the relationship between the friction (F) and carrier concentration (ne) is

$$F = 0.97n_e + 1.23$$
(5)

Therefore, the friction to the carrier concentration approximately follows a linear function of one variable.

Fig. 6: The influence of normal electric field on nanofriction using Raman spectroscopy.
figure 6

a Raman experimental setup. b Raman spectra of atomically thin MoS2 under different Vg. c FWHM and carrier concentration of A1g mode as a function of Vg. d FWHM and carrier concentration of E12g mode as a function of Vg. e Carrier concentration and friction as a function of gate voltage. f Plots of the friction as a function of carrier concentration. g AFM tip sliding on atomically thin MoS2 emitting electron and phonon pairs. h Schematic diagram of the energy dissipation as the AFM tip slides on atomically thin MoS2. Error bars represent standard deviations.

Full size image

Figure 6g shows the schematic diagram of the energy dissipation as the AFM tip slides on atomically thin MoS2 emitting phonon. The phonons produced by friction on atomically thin MoS2 interact with electrons and lead to an additional channel of energy dissipation by EPC, as schematically shown in Fig. 6h. Therefore, the strength of EPC in atomically thin MoS2 was significantly changed by the gate-modulated carrier concentration. The physical picture for the change in nanofriction on atomically thin MoS2 under different Vg was proposed: the instability of the stick-slip behavior would cause local vibration of the crystal lattice and the vibration energy is dissipated by the excitation and propagation of phonons. However, the associated lattice motion is damped by the creation of electronic excitations through EPC in atomically thin MoS2 with high electron doping. Also, the EPC could change the dynamic behavior of lattice motion. The trajectory of a nucleus in atomically thin MoS2 during the friction process follows a Langevin equation25,26. Therefore, the generalization of the Langevin equation can be used to demonstrate the energy dissipation due to EPC with a friction term Ri and a random force ζi25,52,

$$m_i\frac{{\partial v_i}}{{\partial t}} = F_i(t)-{\sum} {R_i({{{\mathrm{t}}}})\nu _i + \zeta _i({{{\mathrm{t}}}})}$$
(6)

where mi is the atom mass, vi is the velocity, Fi(t) denotes the total force exerted on atom (mean force), and Ri is the friction term representing the strength of EPC. ζi(t) is a random fluctuating force and subject to the fluctuation-dissipation theorem53. The random force ζi(t) can be solved with the equation of <ξ(t)ξ(t')≥ 2miRikBTe δ (t − t'), where δ is the Dirac delta function. Ri can be given as follows:

$$R_i = \frac{{m_ig_{ep}}}{{3Nk_B}},$$
(7)

N is the number of atoms. ζi is related to gep and gep is the EPC parameter54, which is \(g_{ep} = \frac{{\pi ^2m_eC_s^2n_e}}{{{{{\mathrm{6}}}}\tau \left( {{{{\mathrm{T}}}}_i} \right)T_e}}\), where me is the effective electron mass, Cs is the speed of sound, ne is the electrons density, and τ(Te) is the electron relaxation time defined as the electron-phonon scattering time. The EPC parameter is proportional to the electron density. Based on the equation of (7), the friction can be given as,

$$R_i = \frac{{m_im_e\pi ^2C_s^2}}{{{{{\mathrm{18}}}}k_B^2N\tau \left( {{{{\mathrm{T}}}}_e} \right)T_e}}n_e$$
(8)

The total friction Ftotal could be divided into two parts including the electronic contribution and phononic consumption. The friction caused by phononic consumption Fph could be described as Equation: \(F_{ph} = \frac{{\pi A}}{{b^2\omega }}\left[ {{{{\mathrm{E}}}}_0 + kT{{{\mathrm{ln}}}}\left( {\frac{\nu }{{\nu _0}}} \right)} \right]\)55. Thus,

$$F_{total} = F_{EPC} + F_{ph} = \frac{{m_im_e\pi ^2C_s^2}}{{18k_B^2N\tau \left( {T_e} \right)T_e}}n_e \times \nu _i + \frac{{\pi A}}{{b^2\omega }}\left[ {{{{\mathrm{E}}}}_0 + kT{{{\mathrm{ln}}}}\left( {\frac{\nu }{{\nu _0}}} \right)} \right]$$
(9)

The \(\frac{{m_im_e\pi ^2C_s^2}}{{18k_B^2N\tau \left( {T_e} \right)T_e}} \times \nu _i\) remains the same a can be treated as a constant α because only the carrier concentration was modulated by the electric field and other parameters such as temperature and velocity were kept the same. Furthermore, the friction caused by phononic consumption also remains the same. Thus, the Fph is also set as a constant \(\beta = \frac{{\pi A}}{{b^2\omega }}\left[ {{{{\mathrm{E}}}}_0 + kT{{{\mathrm{ln}}}}\left( {\frac{\nu }{{\nu _0}}} \right)} \right]\). Then the general formula of friction on atomically thin MoS2 under the electric field could be described as follows,

$$F_{total} = \frac{{m_im_e\pi ^2C_s^2}}{{18k_B^2N\tau \left( {T_e} \right)T_e}}\nu _i \times n_e + \frac{{\pi A}}{{b^2\omega }}\left[ {{{{\mathrm{E}}}}_0 + kT{{{\mathrm{ln}}}}\left( {\frac{\nu }{{\nu _0}}} \right)} \right] = \alpha \;n_e + \beta$$
(10)

If α and β are equal to 0.97 and 1.23, respectively. Then, the friction is linear with the carrier concentration from the Langevin equation which is in accordance with the fitting of friction and carrier concentration.

The strength of electron-phonon coupling in atomically thin MoS2 increases with the increase of gate voltage due to electron doping. Therefore, this lead us to the most likely scenario to explain the increased nanofriction of atomically thin MoS2 under the applied gate voltage. Phonons excited by the mechanical energy of the sliding tip in atomically thin MoS2 are much more likely to scatter with electrons, introducing a more efficient means of dissipating energy12. During the observed stick-slip motion, the lattice is locally distorted and released by the slipping probe tip transferring kinetic energy into lattice vibrations26. For the atomically thin MoS2 under the electric field, the lattice motion is damped by the creation of electronic excitations through electron-phonon coupling. This additional mechanism increases the efficiency of energy dissipation during slip events which are responsible for frictional energy losses.

The atomic-scale stick-slip curves under different gate voltages are shown in Fig. 3a. The Prandtl–Tomlinson model has been greatly accepted for depicting the universal stick-slip phenomena. Since only the carrier concentration is changed, the phononic friction is a constant under different gate voltages. We assume that a linear superposition of the phononic energy dissipation and an independent electronic friction channel caused by electron-phonon coupling (EPC)24,55. Then, the total energy corrugation can be given by Utot = Uph + UEPC, where Uph is the energy corrugation of phononic friction, UEPC is the energy corrugation of electric friction induced by EPC.

Therefore, a modified Prandtl−Tomlinson model was proposed, as shown in Fig. 7a. An AFM tip moves on MoS2 surface can be simplified to the motion of a point mass being dragged over a periodic potential by a supporting body M through a spring. The elastic spring of stiffness k represents the torsional stiffness of the AFM cantilever. The system is characterized by the following potential energy56,57:

$$V = -\frac{{U_{ph} + U_{EPC}}}{2}\cos \left( {2\pi \frac{{x_{{{{\mathrm{tip}}}}}}}{a}} \right) + \frac{1}{2}k\left( {x_{{{{\mathrm{tip}}}}}-x_{{{\mathrm{s}}}}} \right)^2$$
(11)
Fig. 7: Modified Prandtl−Tomlinson model and calculating of the energy corrugation.
figure 7

a Schematic of the modified Prandtl−Tomlinson model describing that the AFM tip moves on the monolayer MoS2. b Energy corrugation Utot as a function of gate voltage. c Energy corrugation UEPC of electronic friction as a function of gate voltage. Error bars represent standard deviations.

Full size image

According to the modified PT model, the maximum lateral force max (Fmax L) during the stick-slip motion is determined by the interface energy corrugation Uph and UEPC. The maximum of the absolute value of the force Fmax L is found at xtip = a/4, and we obtain

$$U_{tot} = {{{\mathrm{a}}}} \times F_L^{{{{\mathrm{max}}}}}/\pi$$
(12)

The Utot was shown in Fig. 7b. The Utot increases significantly under the positive gate voltage and decreases slightly under the negative gate voltage. When the gate voltage is below 0V, the electronic friction was suppressed due to the dissipation of charge carriers and the phonon dissipation is governed by the energy dissipation of friction. Therefore, the energy corrugation at −4 V is approximated as the Uph. For a better analysis of the electronic friction branch, we substract the Uph curve from the total Utot. What remains is the electronic friction contribution as a function of gate voltage in Fig. 7c. By fitting the UEPC as a linear function of the gate voltage, we find that the relationship between the energy corrugation of UEPC and the gate voltage is linear, which is consistent with the relationship between carrier concentration and friction.

The friction tuning effect induced by an electric current was investigated using conductive atomic force microscopy and DFT calculation by Song et al.58. DFT calculations propose that a larger electron density fluctuation during sliding tends to have a larger sliding barrier change resulting in a larger change of friction, which confirmed the contribution of electron density fluctuation to friction. The carrier concentration of MoS2 was tuned based on field effect modulation. Increasing carrier concentrations would increase the electron density fluctuation resulting in larger friction. Wang et al. has performed friction experiments of a single-asperity sliding on a high-Tc superconductor from 40 to 300 kelvin and they found that the electronic friction exceeds 50% of the total friction signal24. Friction on single-layer graphene is found to be a factor of two larger than on bilayer films due to the electron-phonon coupling12. In our manuscript, the phonon dissipation is governed by the energy dissipation of friction as the gate voltage is below 0V due to electron dissipation. The friction could be reduced by 17% under the negative voltage. Also, the nanofriction does not decrease further when the gate voltage exceeds −5 V. As a result, we infer that the electronic friction at the gate voltage of 0V is ~17% and phononic friction 83%. In addition, the charge carriers accumulate and the electron-phonon coupling is enhanced under the positive gate voltage, leading to more efficient energy dissipation due to electron doping. As a result, the electronic contribution dominates the energy dissipation in friction under the positive gate voltage. Considering phononic friction is a constant, the electronic friction to the relative contribution of the two components increases with the increase of gate voltage.

The nanofriction induced phonons in atomically thin MoS2 interact strongly with electrons due to EPC resulting in a new channel for energy dissipation of friction. The nanofriction on atomically thin MoS2 increases with the increase of the carrier concentration, indicating that the energy dissipation of friction is consistent with the strengthening of EPC. The background carrier concentration was reduced by applying the negative Vg. Therefore, the decreased carrier concentration depresses the strength of the EPC to decrease the additional energy dissipation efficiency in atomically thin MoS2. Then, the nanofriction on atomically thin MoS2 correlates strongly with the carrier concentration. Therefore, active controlling of nanofriction on atomically thin MoS2 could be obtained by tuning the carrier concentration based on gate voltage modulation.

Figure. 8a shows 500 × 500 nm2 frictional map (grayscale: bright, high nanofriction; dark, low nanofriction) on the atomically thin MoS2 under the cyclic Vg of 5 V. The Vg was sequentially and dynamically modulated in the order of 0-5-0-5-0-5-0-5-0-5 V. A strip of nanofriction was observed from nanofriction map under the applied electric field. As shown in Fig. 8b, it is clearly observed that the nanofriction increases as the increase of Vg. Also, the changes of nanofriction on atomically thin MoS2 are rapid and reversible during the switch of the Vg. Figure. 8c shows the frictional profiles during the dynamic tuning of Vg between −10 V and 0 V. The nanofriction is reduced reversibly at Vg = −10 V and the nanofriction can also be fully recovered when the Vg return to 0 V, as shown in Fig. 8c. Figure. 8d shows that the nanofriction is controlled stably and reversibly at high Vg, proving the high reliability of this nanofriction-tuning method. Figuer. 8d also shows that the nanofriction response has good repeatability and stability to the variation of Vg. The nanofriction can reduce by about 20% under the negative Vg (Fig. 8c) and increase about five times under the positive Vg (Fig. 8d). In particular, the effect of the negative and positive Vg on the nanofriction have a significant difference. Therefore, actively tuning of nanofriction on atomically thin MoS2 in a dynamic, reversible, and controllable way is achieved based on the field effect modulation of the carrier.

Fig. 8: Nanofriction modulation on atomically thin MoS2.
figure 8

a Mapping of the nanofriction on atomically thin MoS2 modulated dynamically under different Vg. Scale bar: 100 nm. b Corresponding profiles of the nanofriction indicated by the blue arrow line. c The nanofriction on atomically thin MoS2 modulated by applying the negative Vg. d The nanofriction on atomically thin MoS2 modulated by applying different positive Vg (the load for friction test was 10 nN).

Full size image

In summary, the electronic friction and energy dissipation on atomically thin MoS2 were investigated using calibrated AFM under different Vg. The electronic friction and energy dissipation on atomically thin MoS2 correspond strongly with the Vg modulated strength of EPC. The linear fitting of electronic friction and carrier concentration of atomically thin MoS2 was obtained by varying the strength of EPC with controllable carrier concentrations. The friction on atomically thin MoS2 can be tuned dynamically, repeatably, and controllably by gate-induced regulation of the carrier concentration. The electronic friction and energy dissipation of atomically thin MoS2 based on EPC provides a novel method to control friction and provide the possibility for recent emerging applications of superlubricity. The electronic friction could extend the potential application of atomically thin 2D with semiconductors in various MEMS/NEMS to achieve intelligent friction.

Methods

Fabrication of the atomically thin MoS2 and AFM probe calibration

The natural MoS2 bulk crystals used in this study are provided by SPI Supplies Inc. The atomically thin MoS2 was prepared by mechanical exfoliation and then transferred to the p-doped Si substrate with a 300 nm thick SiO2 insulation layer. The Si probes (Multi75Al-G, 3.0 N/m, Budget Sensors) with rectangular cantilevers were used for the nanofriction and topography measurements. The conductive probes with PtIr coating (EFM, Nano World Inc.) were used for surface potential measurements. The normal and lateral forces were calibrated using a noncontact method59.

Topography, friction, and adhesion measurements

The topography and thickness of atomically thin MoS2 were determined by AFM in tapping mode (MFP-3D, Asylum Research Inc). The nanofriction and adhesion measurements were accomplished on atomically thin MoS2 using AFM in contact mode in an ambient environment (temperature ~22 °C, relative humidity ~30%). The nanofriction on atomically thin MoS2 was measured in the scanning area of 500 × 500 nm2 at the scanning speed of 1.25 μm/s. The adhesions were evaluated by the pull-off force from force-distance measurements with a Si probe. Adhesion force was measured five times to take the average value. The SiO2/Si substrate was placed on the conductive gold foil for the connection of the external electric field. The positive and negative values of the gate voltages (Vg) were applied to the conductive gold foil during the nanofriction and adhesion measurements.

Surface potential measurements

The surface potential of atomically thin MoS2 was measured by scanning Kelvin force microscopy (SKPM) under an ambient condition with different gate voltages. The spring constant and resonance frequency of the conductive probe for surface potential measurements was 2.8 N/m and 75 kHz, respectively.

Raman spectroscopy characterization of atomically thin MoS2

Room-temperature Raman spectra were recorded with 532-nm line of an argon ion laser as exciting radiation with a Witec confocal spectrometer using a 50 × long working distance objective. Laser power was kept below 1 mW to avoid heating samples. The positive and negative gate voltages were also applied to the conductive gold foil on the SiO2/Si substrate during Raman measurements.