Introduction

Two-dimensional (2D) heterobilayers (HLs) assembled from atomically thin monolayers (MLs) of transition-metal dichalcogenides (TMDs)1,2 have shown various unique properties of strong interaction with light, fast interlayer charge transfer, and valley-dependent optical selectivity, highly promising for their applications in novel electronic/optoelectronic devices3,4,5,6. Two MLs with a slight lattice mismatch or rotational misalignment brought into contact forming a HL produce a moiré superlattice (mSL)7,8,9 with an additional in-plane periodic potential, and the resulting new length/energy scale provides a powerful means of controlling the quantum phenomena. The moiré period exceeds 100 nm in MoSe2/WSe2 HLs with a small lattice mismatch (<0.2%)10,11. The broad photoluminescence (PL) of the interlayer excitons (IX) commonly observed in these HLs breaks down into many extremely narrow peaks under extremely low optical pumping at low temperature (<4 K)10,12, originating from the excitons trapped in the individual minima of the mSL, called as moiré excitons. The mSL effects were also found in strongly lattice-mismatched (~4%) HLs such as WSe2/WS213 and MoSe2/WS214, where the moiré period is < 10 nm, but their optical behaviors were explained by the hybridization of the IX and intralayer excitons (X), resulting in the formation of hybridized excitons14.

The difference in the lattice parameter between MoS2 and WS2 MLs is only 0.16%15,16,17, indicating negligible lattice mismatch, and their heterojunction is classified as type II. In the type-II HLs, the conduction band minimum (CBM) and the valence band maximum (VBM) are localized to MoS2 and WS2 layers, respectively, and efficient charge transfer/separation occurs between the layers, resulting in the formation of the interlayer excitons with long lifetimes18,19,20. MoS2 and WS2 MLs showed strong PL at ~1.86 and ~1.96 eV21, respectively, corresponding to their intralayer A excitons of MoS2 and WS2 (MoS2-A and WS2-A), but both PL signals were considerably quenched by the heterojunction, resulting from the efficient charge transfer. The charge transfer in MoS2/WS2 HLs was shown to take place within 50 fs upon photoexcitation due to the strong interlayer coupling21,22. This results in a PL band at ~1.42 eV23, smaller than the PL energy of each constituent ML, indicating the formation of an additional state with reduced energy by the heterojunction16,24,25.

It has been expected that the mSL exciton states and multiple interlayer exciton resonances in the HLs strongly depend on interlayer twist angle (θ) between the adjacent MLs16,24,25,26. There have been a few reports on the PL peak shifts by twisted heterojunction of two different TMD MLs at θ far from 0 or 60°, but all of them are redshifts10,11,12,14,27,28. Here, we studied the effect of θ on optical properties of MoS2/WS2 HLs by employing Raman/PL/differential-reflection (DR) spectroscopies and second harmonic generation (SHG) technique, and first observed blue shift of energy and strong enhancement of intensity in the PL by the heterojunction in a particular range of θ. We discuss these novel light-emission behaviors with reference to theoretical predictions on the avoided crossing between the interlayer and intralayer excitons29 and the carrier population change and band edge shifts with respect to θ25.

Results and discussion

Fundamental characteristics of MoS2/WS2 heterobilayers

Triangle-shaped MoS2 and WS2 MLs were grown by NaCl-assisted chemical vapor deposition. More details for the growth are given elsewhere (see Methods section). Triangular-shaped MoS2 flakes were identified by optical microscopy (OM) images with uniform color contrast (Supplementary Fig. 1a). The surface of the MoS2 (or WS2) flake was smooth and flat and no residues were left between the flakes, as confirmed by atomic force microscopy (AFM) images (Supplementary Fig. 1b). The MoS2 flake was shown to be a ML by estimating its thickness (about ~0.8 nm) from the AFM height profile30,31. From the Raman \(E_{2{{{\mathrm{g}}}}}^1\) and A1g modes of the MoS2, observed at 385.8 and 404.4 cm−1, respectively (Supplementary Fig. 1c), their peak separation was estimated to be 18.6 cm−1, further demonstrating the ML nature30,32. To check the uniformity of the crystal in microscale, the Raman mapping was done for the \(E_{2{{{\mathrm{g}}}}}^1\) and A1g modes (Supplementary Fig. 1d, e). The PL spectrum of the MoS2 was peaked at ∼1.86 eV with a shoulder at ∼1.99 eV (Supplementary Fig. 2), corresponding to MoS2-A and -B (intralayer B excitons) direct transitions of the MoS2 ML, respectively33. The PL mapping images of the peak energy and intensity also demonstrated the uniformity of the samples. Similarly, the crystallinity and homogeneity of the triangular WS2 flakes were confirmed by OM, AFM, Raman, and PL (Supplementary Fig. 3). The thickness of the WS2 flake was estimated to be ~0.86 nm, and the Raman intensity of the \(E_{2{{{\mathrm{g}}}}}^1\) mode at 351.4 cm−1 was two times larger than that of the A1g mode at 416.2 cm−1 with their resulting frequency difference being 64.8 cm−1, confirming the ML nature of the WS2 flake34. The prominent PL peak observed at 1.98 eV corresponds to the excitonic emission of the WS2 ML33,35.

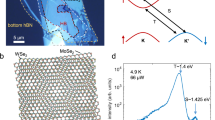
Figure 1a shows an OM image for two typical WS2/MoS2 HLs at θ = 0 and 30°, formed on SiO2/Si substrate. The larger bottom ML is MoS2 whilst the smaller top MLs are WS2. The θ was extracted by comparing the orientations of the flakes in the OM image. It has been shown that triangular TMD flakes have sharp or diffuse zigzag edge terminated with transition-metal or chalcogen atom, respectively, as shown in the microscopy images27,36,37. Considering these results, the θ between the WS2 and MoS2 flakes was determined with around 1° accuracy (Supplementary Fig. 4), but the uncertainties in the θ measurements exist inherently because the type of the edge was not clear frequently, depending on whether either transition-metal or chalcogen atom was located at the periphery. To make up for such possible inaccuracies, polarization-dependent SHG measurements were performed (Supplementary Fig. 5). The SHG signals provide useful information on the crystal orientation and homogeneity of TMDs as well as their thickness and stacking sequence38,39. Figure 1b shows a SHG mapping image for the same sample in Fig. 1a, made by assembling the SHG intensities averaged on 30 sample points of the ML and HL regions. From the characteristic six-fold SHG patterns, as shown in Fig. 1c, the θ values of 0 and 30ο, obtained from the OM image, were more accurately corrected to 0 ± 0.6 and 30 ± 1.4ο, respectively. Following this procedure, the θ values could be obtained within ±2o accuracies for the differently oriented WS2/MoS2 HLs. Here, it should be noted that the SHG intensity is normalized in Fig. 1c, but it was clearly shown to be stronger at 0o than at 30o in the real data (Supplementary Fig. 6). We also confirmed this θ-dependent behavior of the SHG intensity for various θ values (Supplementary Fig. 7).

Fig. 1: Twisted MoS2/WS2 heterobilayers.
figure 1

a, b Optical microscopy image (a) of typical bilayers at θ = 0 and 30°, and b corresponding SHG mapping image. c Polar plots of the polarization-resolved SH intensity as a function of azimuthal angle between the incident laser polarization and the armchair direction for the bilayers at θ = 0 and 30°. d Raman spectra of typical MoS2 and WS2 monolayers, and the MoS2/WS2 bilayer at θ = 0°. e Photoluminescence spectra of the MoS2 and WS2 monolayers, and the MoS2/WS2 bilayers at θ = 0 and 60°. Here, the PL peaks of the MoS2 and WS2 intralayer excitons (MoS2-A and WS2-A) are indicated.

Full size image

As shown in Fig. 1d, the \(E_{2{{{\mathrm{g}}}}}^1\) and A1g Raman modes, typical of MoS2 MLs, are observed in the bottom bare MoS2 ML region whilst two additional Raman peaks are found at ~351 and ~416 cm−1 in the HL region, corresponding to the wavenumbers of the \(E_{2{{{\mathrm{g}}}}}^1\) and A1g modes of the top bare WS2 ML region, respectively. Figure 1e shows room-temperature (RT) PL spectra of the MoS2 and WS2 MLs, and the HLs at θ = 0 and 60o. The major PL peaks at 1.86 (red curve) and at 1.98 eV (blue curve) arise from the resonances of MoS2-A and WS2-A, respectively21,22,23. The PL intensity of the WS2 ML is 15 ~ 20 times larger than that of the MoS2 ML. By the heterojunction of the MLs at θ = 0 and 60o, the MoS2-A PL peak slightly decreases whilst the WS2-A PL peak is 20 times quenched, resulting from the efficient interlayer charge transfer between the layers21,33. In principle, PL is quenched by two mechanisms in a HL: energy transfer and charge transfer22. Energy transfer quenches only the PL from a higher energy transition (the 1.98 eV PL in WS2), while it tends to enhance PL from a lower energy transition (the 1.86 eV PL in MoS2). In contrast, charge transfer quenches PL from all transitions. This explains why the PL of WS2-A is quenched more significantly than that of MoS2-A in MoS2/WS2 HLs. The Raman and PL behaviors of the HLs at θ = 0 and 60o are almost consistent with previously reported results16,21,22,23,40.

Blue-shifted and strongly enhanced light emission

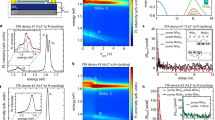
In the next step, the PL behaviors of the HLs were studied for 0 < θ < 60o. As a typical case, Fig. 2a–d shows an OM image and corresponding SHG/PL peak/PL intensity mapping images, respectively for the HL at θ = 57ο. In the HL region, the PL peak blueshifts (or redshifts) with respect to that of the MoS2 ML (or the WS2 ML), and the PL intensity is larger than even that of the WS2 ML. The PL mapping images further show that the PL emission is almost uniform over the entire HL region, which confirms spatial/spectral homogeneity of the PL over the μm-length scale, consistent with the Raman mapping image (Supplementary Fig. 8). Figure 2e shows typical PL spectra of the HLs for various θ between 0 and 60o together with those of the isolated MoS2 and WS2 MLs. The PL spectra at 0 < θ < 60o look very broad with only one peak, different from the cases at θ = 0 and 60 o, as shown in Fig. 1e. In the range of θ near 0 or 60ο, for example, at θ = 3 or 57ο, the peak energy (1.89 or 1.96 eV) is larger than that of the MoS2 ML (1.86 eV), but is smaller than that of the WS2 ML (1.98 eV). In contrast, in the intermediate range of θ, for example, at θ = 23ο, the peak energy (2.01 eV) is larger than even that of the WS2 ML.

Fig. 2: Photoluminescence of twisted MoS2/WS2 heterobilayers at room temperature.
figure 2

a–d Optical microscopy image (a) of a typical bilayer at θ = 57° and corresponding (b) SHG, (c) PL peak energy, and (d) PL peak intensity mapping images. e PL spectra of typical MoS2 and WS2 monolayers, and MoS2/WS2 bilayers at θ = 3, 23, and 57°. Here, the PL peaks of the MoS2 and WS2 intralayer excitons (MoS2-A and WS2-A) are indicated. f Shifts of the PL spectra by successive variation of θ from 3 to 57°. Here, the locations of the WS2-A peak are drawn by the guiding line. g, h PL peak (g) energy and (h) intensity as a function of θ.

Full size image

Figure 2f shows normalized PL spectra of the HLs for various θ in the range of 3 – 57o. The PL peak sequentially moves as the stacking approaches either the lattice alignment (towards θ = ∼0ο) or anti-alignment (towards θ = ∼60ο) between the layers. The θ-dependent PL peak shifts are summarized in Fig. 2g, in which two distinct trends can be noted: a steep variation (about 120 meV) in the peak energy as θ gets closer to 15 or 52° from 3 or 57°, respectively and a plateau at around 2.01 eV in the θ range from 15 to 52°. Here, for higher reliability, the peak energy was averaged on ~30 points of one sample, and 3 ~ 15 samples were used to obtain the data points at a single θ. Figure 2h summarizes the ratio of the integrated PL intensity (I) normalized to that of the WS2 ML (I0), for various θ from 3 to 57ο. The PL intensity was integrated in the range of 1.7~2.1 eV for I and I0. The I/I0 shows sharp changes as θ gets closer to 15 or 52° from 3 or 57°, respectively, similar to the θ−dependent PL peak shifts, as shown in Fig. 2g. Especially, in the range of 15 ≤ θ ≤ 52ο, the PL intensity is ∼4 or 80 times enhanced compared to that of the isolated WS2 or MoS2 ML, respectively. These θ-dependent abrupt changes were not observed in MoS2/MoS2 homobilayers (Supplementary Fig. 9).

Differential-reflectance spectra and theoretical explanations

Figure 3a, b compares PL and DR spectra at 80 K for the isolated MoS2 and WS2 MLs (see Supplementary Fig. 8 for the spectra at RT). The DR is usually regarded as the absorption coefficient, α(λ), based on the following equation41: \(\frac{{R - R_0}}{R} = \frac{{4n}}{{n_0^2 - 1}}\alpha \left( \lambda \right)\), where R/R0 and n/n0 are the DR intensities reflected by the flake/the substrate and their indices, respectively. It is well known that optically excited electrons and holes are thermalized to lower energy states before they recombine radiatively, as also confirmed in our samples by the energy difference between the PL and DR peaks at RT (Supplementary Fig. 10). Interestingly, the Stokes shift is not observed for the MoS2 ML at 80 K, as shown in Fig. 3a. The band gap of the semiconductors increases with decreasing temperature, based on the Varshni formula42, resulting from the decrease of the electron-phonon interaction and the contraction of the lattice at lower temperature. This explains why the PL as well as the DR blueshifts with decreasing temperature, as shown in Fig. 3a (and Supplementary Fig. 10a), where the PL and DR peak shifts of MoS2 can be estimated as follows. From 300 to 80 K, the A and B bands of the DR blueshift from 1.894 and 2.037 to 1.929 and 2.083 eV, respectively, while those of the PL blueshift from 1.864 and 1.999 to 1.929 and 2.074 eV, respectively. The temperature rates of the blueshifts cannot be same for the DR and PL due to their different physical mechanisms. Based on these considerations, it seems that the PL energy identical to the DR energy at low temperature for the MoS2 is just a coincidence and not based on a particular physical principle, consistent with the detailed temperature dependences of the PL and DR spectra, as previously reported for various 2D materials43.

Fig. 3: Differential reflectance of twisted MoS2/WS2 heterobilayers at 80 K.
figure 3

a, b DR and PL spectra of (a) typical MoS2 and (b) WS2 monolayers. c DR spectra of typical MoS2 and WS2 monolayers, and a typical MoS2/WS2 bilayer at θ = 27°. The spectrum is resolved into fitted curves, and the DR peaks of the MoS2 and WS2 intralayer excitons (MoS2-A/-B and WS2-A) are indicated. d Shifts of the DR spectra by successive variation of θ. Markers and dashed lines show the P1/P2/P3 and MoS2-A/WS2-A peaks, respectively. e P1, P2, and P3 peaks as functions of θ. Dashed lines show the locations of the MoS2-A and WS2-A peaks.

Full size image

Figure 3c compares DR spectra of the HL at θ = 27o and the MLs. The DR spectrum of the HL is well resolved into three spectra peaked at P1, P2, and P3 by a fitting program. In the literatures, two additional absorption peaks at higher energies were also observed for WSe2/WS213 and MoSe2/WS2 HLs14, possibly resulting from the folded excitonic bands, in contrast with the observation of only a single absorption peak attributed to the lowest energy excitonic transition in a WSe213 or MoSe2 ML14. The spectral information can be extracted in more detail from DR spectra than PL spectra. The energy of the P1 peak is only ~20 meV larger than that of the MoS2-A peak, and so the P1 peak seems to originate from the MoS2-A peak. The P3 peak is close in energy to the MoS2-B and WS2-A peaks whilst the P2 peak is located at a position about 50 meV lower than both the ML peaks.

Figure 3d shows the DR spectra of the HLs for various θ between 0 and 60° together with those of the isolated MoS2 and WS2 MLs. Figure 3e summarizes the shifts of the P1, P2, and P3 peaks as functions of θ. The P1 peak suddenly blueshifts as θ deviates from 0 or 60°. The higher energy peaks (P2 and P3) are almost degenerate at θ near 0 or 60°, but they are split in the intermediate range of θ (≈20 ∼ 50°). At some of these orientations, the P3 peak almost reaches the level of the WS2-A peak. The splitting can be attributed to the avoided crossing between the X of WS2-A and the IX. Such avoided crossing is absent at almost aligned & anti-aligned (θ ≈ 0 and 60o) orientations because the IX lies at an energy far below the X of the constituent MLs29. The IX varies with θ due to the θ dependence of the distance between the band edges of the two layers as well as of the Brillouin zone of the mSL. As a result, the energy of the IX shifts toward that of the WS2-A at θ between 15 and 52° and the avoided crossing of the IX and X is induced by the interlayer hole tunneling29, thereby making the DR peak at higher energy split into two different ones, P2 and P3, as shown in Fig. 3d. The PL spectra of the HLs (Fig. 2f) mainly originate from the transitions associated with the P2 and P3 peaks because the PL intensity of the WS2 ML is much stronger than that of the MoS2 ML (Fig. 1e). In a different view, the energy of the P3 peak is comparable to that of the WS2-A DR peak (Fig. 3e) whilst the PL peaks of the HLs are located at the energies higher than the WS2-A PL peak (Fig. 2f). This suggests that the degree of the thermalization seems to be smaller in the HLs than in the WS2 ML, which might be another reason for the blue shift of the PL by the heterojunction.

At θ ≈ 0 and 60o, the IX is dark since the interlayer interaction near the Brillouin zone corners of TMDs is weak. At θ between 15 and 52o, however, the conduction bands of the two monolayers overlap in energy. Thus, the X and IX associated with the bands form hX, thereby (i) making the X and IX move in opposite direction in energy by avoided crossing and also (ii) the IX bright by the band mixing and the formation of van Hove singularity. If the oscillator strength of the IX is comparable to that of the WS2-A, then the ~4I0 light will be emitted, as shown in Fig. 2h, which is consistent with previously reported theoretical prediction on the transition of mixed excitons44. The origin of the peak splitting of the DR peaks P2 and P3 (resulting blueshift of the PL) and the enhancement of the PL intensity at 15° ≤ θ ≤ 52° can be explained in more detail by a decoupled band scheme in the monolayer Brillouin zone of each layer (See Supplementary Theoretical Explanations).

In conclusion, we have shown blue shift of energy and strong enhancement of intensity in the PL by twisted heterojunction of MoS2 and WS2 MLs in the θ range from 15 to 52°, and explained their mechanism based on the optical transitions detailed in the DR. The blue shift of the PL peak was attributed to the avoided crossing of the X and IX excitons by the energy shift of the IX toward the X. The enhancement of the spectral intensity originated from the population change of charge carriers by the band edge shifts and the constructive interference of the oscillator strengths of the X and IX. This novel light-emission behavior may open the way to extendable tuning and strong enhancement of light emission from two-dimensional semiconductors by their twisted heterojunction in a proper θ range, very promising for the optoelectronic device applications.

Methods

Materials preparations

Triangle-shaped monolayers (MLs) of MoS2 and WS2 were produced by NaCl-assisted chemical vapor deposition growth. MoS2 MLs were grown on 300 nm SiO2/Si wafers by vaporization of mixed powders of MoO3, S, and NaCl in a quartz tube furnace under controlled gaseous environment. NaCl in the growth process was found to play a vital role in lowering the growth temperature (T)45,46. A typical run of growth was done by loading 12 mg MoO3 + 18 mg NaCl3 powder in one boat at the high-T zone and 40 mg S powder in the other boat at the low-T zone within the same quartz tube. The distance between the boats were about 15 cm, and the heating rate of all reactions was 25 °C min−1. A piece of SiO2/Si substrate was placed at the downstream location close to the high-T boat. The furnace was heated to 150 °C at a rate of 25 °C min−1 and kept at this temperature for 20 min. The furnace was then heated to 750 °C and kept at this temperature for 10 min for the growth of the MoS2 ML. All the reactions were carried out at atmospheric pressure. The vapor-phase reactants were transported by Ar gas flow at 50 sccm, and the sulfurization was carried out by flowing H2 reductant gas at 10 sccm, thereby facilitating the growth of the 2D crystals at the growth region. At the end of the growth, the furnace was left to naturally cool down to room temperature. For WS2 growth, mixture powder of 30 mg WO3 + 15 mg NaCl and 70 mg S powder were used. The furnace was heated to 800 °C and was maintained at the same T for 5 min under a mixed flow of Ar and H2 gas at 10 and 20 sccm, respectively. For fabrication of twisted heterobilayers (HLs), the ML MoS2 flakes were transferred onto another 300 nm SiO2/Si substrate using a wet-transfer process with poly(methyl methacrylate) (PMMA, sigma Aldrich) as a sacrificial layer. A PMMA solution was spin-coated onto the MoS2/SiO2/Si substrate at 4000 rpm for 60 s. The PMMA/MoS2/SiO2/Si stack was baked at 120 °C for 30 min and then floated in buffered oxide etchant (BOE 6:1, J. T. Baker) solution to separate the PMMA/MoS2 flake from the substrate. The floating PMMA/MoS2 flake was transferred onto a prepared SiO2/Si substrate and consecutively annealed at 75 oC for 4 h and at 180 oC for 2 h. After the annealing, the PMMA layer was dissolved in acetone. The MoS2/SiO2/Si stack was then cleaned by using isopropyl alcohol, and further heated at 200 oC for 5 min by rapid thermal annealing to remove the remnants on the sample surface and enhance the adhesion between the flake and the substrate. The floating PMMA/WS2 flake was also prepared through the similar process, and transferred onto the prepared MoS2/SiO2/Si substrate to form a HL, which was sequentially annealed at 75 oC for 4 h and at 180 oC for 2 h. Finally, the PMMA layer was dissolved in acetone, and the substrate was cleaned using isopropyl alcohol.

Characterizations

SHG measurements were performed on Zeiss 780 confocal microscopy. The fundamental laser field was provided by a tunable pulse Ti:sapphire laser with a pulse width of 150 fs and a repetition rate of 80 MHz. A 50× confocal objective lens (NA = 0.85) was used to focus the laser pulse to the sample. The SHG signals taken at a fundamental laser wavelength of 900 nm were collected by the same objective, separated by a beam splitter, and filtered by suitable optical filters to block the reflected fundamental radiation. For polarization-resolved SHG, an analyzer (polarizer) was used to select the polarization component of the SH radiation parallel to the polarization of the pump beam. The sample was rotated by a rotational stage to obtain the orientation dependence of the SH response. Raman and PL spectroscopy were carried out using a confocal Raman/PL microscope (HEDA, NOST, Korea) with 532 nm laser. The laser light with a typical incident power of 100 μW was linearly polarized and focused to a spot size of <1 μm by a 100× objective lens (numerical aperture, 0.9). The sample was mounted on a piezo-stepper table and scanned under the microscope. The spatial resolution of this setup is about 500 nm. The PL emission (or Raman scattering) signal was collected with the same objective, dispersed with a monochromator, and detected using a charge-coupled device (Andor Technology). Differential reflectance was measured in the same apparatus used for the PL/Raman spectroscopy. The low-temperature spectra were measured at 80 K on a cooled liquid-nitrogen stage (Linkam stage, LTS420). A ×50 (NA = 0.50) long working distance objective was used to focus the laser beam onto the sample.