Introduction

Excitons are charge-neutral excitations and can be well approximated by the eigenstates of a two-particle Hamiltonian. An electron–hole pair can form an excitonic bound state as the Coulomb interaction becomes strong. These two-particle bound states can form deep inside one-particle electronic bandgap in insulators. Usually in systems where the valence and conduction states are mostly dominated by s and p electrons, the Coulomb interaction is strongly screened and the excitons become weakly bound. Such excitons are referred to as Mott–Wannier excitons1 owing to their delocalized nature in real space, with diameters up to few nanometers. These excitons are heavily studied in the literature and usually their binding energies range between tens of meV to 500 meV2,3. The excitons observed in transition metal dichalcogenides2,3, LiF4 are the prototypical examples of Wannier–Mott excitons. Only the bottom of the conduction band and the top of the valence band take part in their formation. Nevertheless, as systems become more strongly correlated, for example, in systems with low-energy flat d-states, the Coulomb interaction between electron and hole increases and they can have large binding energies with a diameter approximately that of an atom in an extreme case. Such strongly localized excitons can have binding energies ~1 eV or more and they are referred to as Frenkel excitons5,6,7. They are heavily studied in molecular systems8,9,10 that are far from the band limit. In a crystalline environment where a band picture is applicable, an entire range of bands4 that contain character of the orbital where the exciton predominantly resides can contribute to their formation, in strong contrast to the Wannier–Mott excitons.

Recent observations of excitons with high-binding energies in two-dimensional ferromagnetic monolayers of CrX311,12 have rekindled the investigation of Frenkel excitons in real materials. In a purely atomic picture, the low-energy manifold of these systems are determined by the Cr-3d t2g↑ valence orbitals that contributes to magnetic moment of 3 μB/Cr atom and the Cr-3d eg↑ conduction orbitals. In a series of recent experimental studies that perform controlled photoluminescence and other optical measurements on these 2D magnets, excitons are observed at ~1 eV11,12 while the electronic band gaps of these systems are in the range of ~3–5 eV. These materials are, however, not new and their bulk variants had been studied for long with the earliest studies dating back more than half a century13,14,15,16,17. To realize these magnets in their 2D variant is very recent as ferromagnetism (FM) in a monolayer CrI3 was first reported in 201718,19, which was followed by observation of FM in CrBr311,20, CrCl321 and many other compounds22,23,24,25,26. Bulk and layered variants of the same compound have different electronic band gaps owing to differences in the screening environment originating from their effective dimensionality. Going from bulk to monolayer the electronic screening reduces significantly, leading to a screened Coulomb exchange that is larger than the bulk. Nevertheless, the observation of the same deep-lying excitons at almost the same energies both in bulk and monolayer (ml-) CrX3 is intriguing and suggests that these excitons are Frenkel-like and, could probably be, even the extreme limit of that where they emerge purely from the atomic d–d transitions12.

In a recent work27, we showed that both the electronic band gaps and the halogen components in the valence band manifold changes significantly in ml-CrX3 depending on the nature of the ligand (X) atom. There is significant hybridization of the Cr-3d states with the X-p states and the degree of hybridization increases significantly in the sequence Cl → Br → I. In the present work, we show that this hybridization fully controls the exciton intensity, and also to some extent its position.

We employ our advanced many-body perturbative Green’s function-based approach and show how in these materials excitons with high-binding energies are sensitive to fine details of the two-particle Hamiltonian. Following our earlier work27, we employ three different levels of theory: the local-density approximation (LDA), quasiparticle self-consistent GW theory28,29,30 (QSGW), which, in contrast to conventional GW, modifies the charge density and is determined by a variational principle31, and finally an extension QS\(G\widehat{W}\) of QSGW, where the polarizability needed to construct W is computed including vertex corrections (ladder diagrams) by solving a Bethe–Salpeter equation (BSE) for the two-particle Hamiltonian32. The electron–hole two-particle correlations are incorporated within this self-consistent ladder-BSE QS\(G\widehat{W}\) implementation32,33 within the Tamm-Dancoff approximation34,35. As the present work is a study of excitons, we consider here only QS\(G\widehat{W}\) calculations. A crucial difference in our implementation of QS\(G\widehat{W}\) from most other implementations of BSE is that the calculations are self-consistent in both self-energy Σ and the charge density27,36. The effective interaction W is calculated with ladder-BSE corrections and the self-energy, using a static vertex in the BSE. G, Σ, and \(\widehat{W}\) are updated iteratively until all of them converge. Thus, in contrast to most recent GW studies37,38 our calculations are completely parameter-free and have no starting point bias. In each cycle, the RPA polarizability is made anew, which determines the RPA W. In each cycle the four-point polarizability is recomputed from the (newly updated) static part of W, to update \(\widehat{W}\). Moreover, we checked the convergence in the QS\(G\widehat{W}\) bandgap27 and exciton positions by increasing the size of the two-particle Hamiltonian. We increase the number of valence (v) and conduction (c) states and observe that for all materials the QS\(G\widehat{W}\) bandgap stops changing once 24 valence and 14 conduction states are included in the two-particle Hamiltonian. This stands in stark contrast to the weakly bound case. It reflects the atomic molecular-like picture where any state with significant orbital character participating in the exciton (Cr-3d or X-p) modify it, not just the band edge states as in the Wannier picture. This allows us the flexibility to pin down the orbital characters that determine the position and intensities of the excitons.

Results and discussion

Dielectric response in bulk and monolayer

Within QS\(G\widehat{W}\), the Coulomb interaction \(\widehat{W}\) softens in comparison to QSGW, since the screening is enhanced by the electron–hole attraction, as captured by the ladder diagrams. The electronic bandgap reduces roughly by 20% within QS\(G\widehat{W}\) compared to QSGW for CrX3 both in their bulk and monolayer variants (see Table 1). In other strongly correlated materials, we have observed the electronic band gaps to reduce by 10–20% (material-dependent)32,39,40 within QS\(G\widehat{W}\) compared to QSGW. We compute the macroscopic dielectric response Imϵxx with the perturbing electric field applied along the (100) direction of the material, with the QS\(G\widehat{W}\) electronic one-particle eigenfunctions assuming the optical vertex Γ = I (identity matrix) and also using the explicitly computed Γ. The excitons inside the one-particle bandgap (E ≤ Eg) can only be present in the second case, and not in the first case where the optical transitions can only occur at or beyond the one-particle bandgap (E ≥ Eg).

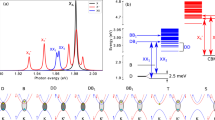
Table 1 Electronic band gaps in bulk and monolayer.
Full size table

Γ induces dramatic optical spectral weight transfer and series of excitons emerge inside the one-particle bandgap ≤Eg in Fig. 1. The optical weight transfers the most for X = Cl and the least for X = I. A series of exciton peaks can be observed in all cases inside the gap. Zoom into the low-energy (0−2 eV) part of the optical spectra, we observe two deepest lying excitons ex1 and ex2 (see Fig. 2) that are robust across all cases and also for both bulk and monolayer variants of CrX3. We observe a weak redshift of ~0.2 eV of these exciton peaks as the electronic screening reduces going from bulk to monolayer. From the deepest lying exciton ex1 position Eex and the electronic bandgap Eg at the QS\(G\widehat{W}\) level, we can compute the highest exciton-binding energies as Eb = Eg − Eex. Eb enhances significantly in going from bulk to monolayer (Table 2) since lesser screening implies stronger exciton binding in the ml. Note, although apparently Eex remains invariant in bulk and ml, both Eg and Eb are enhanced in the ml. Similar observations are made in earlier studies on dichalcogenides across different dimensions41.

Fig. 1: Optical response in bulk and monolayer.
figure 1

Imaginary part of macroscopic dielectric response Imϵxx with the perturbing electric field applied along the (100) direction of the material, for free-standing monolayers (ml) of CrX3 with (a) X = Cl, (b) X = Br, (c) X = I and bulk CrX3 with (d) X = Cl, (e) X = Br, and (f) X = I. The orange color stand for QS\(G\widehat{W}\) vertex Γ corrected optical response, while the green color stands for the vertex replaced by an identity matrix I effectively making it a RPA optical response with QS\(G\widehat{W}\) one-particle eigenfunctions. Energy-dependent optical broadening that linearly varies from 2 milli-Hartree at ω = 0 and 50 milli-Hartree at ω = 13.6 eV is used.

Full size image
Fig. 2: Robust two-peak deep-lying excitonic structure across bulk and monolayer.
figure 2

The low-energy (0−2 eV) part of imaginary part of macroscopic dielectric response Imϵxx with the perturbing electric field applied along the (100) direction of the material, for bulk and free-standing monolayers of CrX3 with (a) X = Cl, (b) X = Br, (c) X = I. Optical broadening of 2 milli-Hartree is used at all energies. The intensities of the peaks are multiplied by some constant factors to bring them to the same scale.

Full size image
Table 2 Exciton-binding energies in bulk and monolayer.
Full size table

Robust two-peak structure of deep-lying excitons in bulk and monolayer: experiments and theory

In bulk, these two exciton peaks (ex1,2) are experimentally well established in CrCl3 and CrBr3 from a series of works13,14,15,16,17 performed between 1960’s and 1980’s. In a recent work42 on CrCl3−xBrx, the same peaks are observed again, and also going from x = 3 to x = 0 a weak blueshift in the peak positions can be noticed. Within our parameter-free approach, we can reproduce the two peaks in both X = Cl and Br and also their relative spacing and intensities agree almost perfectly (see Fig. 3). Some of the crucial features like weak blue-shifting of the exciton peaks and change in their relative spacing in CrCl3 compared to CrBr3 are also reproduced in our calculations. However, these two peaks in our calculations are ~0.5 eV too deep compared to the experimental findings. The position of these excitons change and they become systematically red-shifted as more screening channels are included in the two-particle Hamiltonian we solve using QS\(G\widehat{W}\). As we show in the Supplemental Material, the two peaks already form when the two-particle Hamiltonian contains the minimal six valence bands (v) and four conduction bands (c), which are mostly of Cr-dt2g↑ character and Cr-deg↑ character. So these exciton peaks are triplet in nature and emerge from the 3dt2g−eg transitions within the bands of mostly Cr character. They redshift in tandem as two-particle Hamiltonian includes more bands.

Fig. 3: Benchmarking against experimental optical absorption in bulk CrCl3, CrBr3.
figure 3

Comparison between the adopted optical absorbance data from the recent experimental work on CrCl3−xBrx42 against our theoretical results. The theoretical spectra for Imϵxx is rigidly blue-shifted by ~0.5 eV as our exciton peaks from v24c14 were too deep compared to experiments. Note that the need for such manual blue-shifting would not emerge required if we used the dielectric response computed from a smaller two-particle Hamiltonian, say v12c14 (see Supplemental Material).

Full size image

In a recent photoluminescence (PL) study on ml-CrBr3 by Zhang et al.11, the authors observe a peak at 1.35 eV. They also observe that the PL peak energy is almost invariant of the thickness of the sample (thickness ranging between 6 and 73 nm), which suggests a localized transition. Based on that they argue that this transition is consistent with an atomic d − d transition. They further argue that since the Laporte rule prohibits such transition based on symmetry considerations, to relax the rule symmetry breaking must be introduced via at least one mechanism, such as spin–orbit coupling, Jahn–Teller distortion and formation of odd-parity phonons12 as we noted in the introduction. They observe a broad PL linewidth and argue that it serves as the evidence for the strong vibrionic coupling, resulting in photon sidebands. They also note that the absorption peak that Dhillon et al.13 observed at 1.67 eV in their work from 1966 in bulk CrBr3 is fundamentally the same peak Zhang et al.11 observes at 1.35 eV in ml-CrBr3, which is assigned to the absorption to the4T2 state at 1.5 K. They argue, further, that the Stokes shift of 320 meV, between absorption and PL peaks of Dhillon et al. and Zhang et al. respectively, is due to the strong electron–lattice coupling. Similar optical absorptions to that of Dillon et al.13 is also confirmed in a recent study on bulk CrBr342.

We agree with the general argument of Seyler et al.12, namely that some mechanism is needed to reduce the symmetry and to allow for d–d transitions. Our theoretical results are fully consistent with experimental observations, without the need for more commonly cited sources of symmetry reduction—spin–orbit coupling, lattice relaxations, or phonons. We find that indeed, the low-lying excitons ex1 and ex2 are robust in both bulk and monolayer, with modest differences in their position. Nevertheless, the symmetry-breaking mechanism, as we show, is primarily the dp hybridization between Cr and ligand states. Spin–orbit coupling is not fundamental to the emergence of these exciton peaks, however, they are certainly important in making these excitons “bright”. A strictly “triplet” exciton can not be “bright” since photons have spin angular momentum of ∣1∣. So, even though, spin–orbit coupling is not fundamental as the symmetry-breaking mechanism that relaxes Laporte rule, plays an important role in determining how bright they are.

We note in passing that the present simulations for a free-standing monolayer with a 60 Å vacuum, do not precisely correspond to a monolayer on a substrate. The substrate effect is likely to be nonnegligible in real systems, since even in the absence of significant covalent bonding to modify the energy band structure, the substrate will increase the dielectric response which should reduce the excitonic binding energy. This could be one reason for the slight overestimate of our predicted binding energy in the ml case. However, later in the paper, we discuss the intricate details of the vertex that we consider as one important reason for this overestimation in Eb. While the issue of the “exact position” of such excitons will be discussed in the following sections, clearly, their intensity drops rapidly from bulk to monolayer. Note in Fig. 2 the monolayer intensity is scaled differently to compare against the bulk. This is again fully consistent with experimental observations (see Fig. 1b in Zhang et al.11) and is probably one important reason why in ml-CrX3 careful PL experiments are needed to pick up these weak exciton intensities, while the conventional absorption or reflection spectroscopy is enough to pick up the excitons in bulk.

Before proceeding, we attempt to benchmark our results for CrI3 against the existing body of literature. In a recent PL study on ml-CrI312, an exciton peak is observed at 1.10 eV, and the position hardly changes as the thickness of the sample is increased (see Fig. 4d in Seyler et al.12). From our calculations we also observe the lowest energy exciton ex1 position at 1.0 eV which is robust across bulk and monolayer variants, much like CrCl3 and CrBr3. We perform a thorough benchmarking of our theoretical optical spectra against what is observed in recent experiments and the agreement is excellent for all energies up to ~3.5 eV (see Fig. 4). Also in the study by Seyler et al. where the PL intensities are shown for the 1.10 eV peak for bulk, monolayer and layers of different thickness a dramatic drop in the PL intensity can be observed as one goes from bulk to ml limit. This is fully consistent with our calculations (see Fig. 2c): for the same material the ex1,2 peaks can be ~10 times more intense in bulk compared to its ml counterpart. Among all these materials, the excitons are the most intense in CrI3 (see Fig. 2). This can be observed also in the old studies on the bulk samples13,14. This is again consistent with our calculations (see Fig. 2a, c) where the exciton peaks are the least intense in X = Cl and most intense in X = I. As we show, between ml-CrCl3 and ml-CrI3, the intensity of ex1 varies by a factor of ~10. This is a signature of the fact that although these two deepest lying excitons in all materials originate fundamentally from transitions between Cr-dt2g↑ and Cr-deg↑ states, their intensities are directly proportional to the hybridization of the atomic states with the environment. The (Cr-d, X-p) hybridization increases in the sequence Cl → Br → I, and is responsible for the enhancement in the ex1 intensity leading to brighter excitons. X = Cl is the closest to the purely atomic scenario where the hybridization Cl-p–Cr-d splitting is largest. To reach an unambiguous conclusion we need to perform a further careful analysis of the exciton spectral weights of all these excitons with high-binding energies (ex1,2,3) in the entire class of these bulk and ml magnets. This allows us the opportunity to pin down both their fundamental nature and sensitivity to the ligand states.

Fig. 4: Benchmarking against experimental optical absorption in monolayer CrI3.
figure 4

Comparison between the adopted differential reflectivity data combined with low-energy photoluminescence data from the recent experimental work on ml-CrI312 against our theoretical Imϵxx results. The theoretical spectra for Imϵxx are rigidly blue-shifted slightly as our exciton peaks from v24c14 were by ~0.2 eV too deep compared to experiments. The theoretical data for different optical broadening schemes are also plotted on top of the adopted experimental data.

Full size image

Momentum-space structure of Frenkel and Wannier–Mott excitons

We analyze which band pairs and k-points contribute to the Imϵxx(ω) exciton spectrum integrated over narrow energy ranges near the peaks of the exciton spectrum. We divide the QS\(G\widehat{W}\) exciton region in separate intervals depending on where the three deepest exciton peaks reside. For example in ml-CrCl3, the windows would be [0.6 − 1.4], [1.45 − 2.25], and [2.5 − 3.36] eV, corresponding each to a separate peak in the optical spectrum. Figure 5 shows which band states (n, k) contribute to the exciton eigenvalues. We obtain this figure by using the eigenvectors of the two-particle Hamiltonian as a weight at each k and band n and the relevant eigenvalues in a given energy range. This is then visualized as the size of the circles on the band structure. The valence bands of primarily of Cr-dt2g↑ characters and conduction bands of primarily Cr-deg↑ characters contribute to the ex1 formation in the window [0.6 − 1.4] eV. Intriguingly enough, ten entire bands (v6 and c4) contribute almost uniformly (see Fig. 5) across the Brillouin zone to the ex1 spectral weight. This is true for ex2 in the window of [1.45 − 2.25] as well, except for parts of the conduction and valence bands (third and fourth conduction bands counted from the conduction edge, third, forth, fifth, and sixth valence bands counted from the valence band top) contribute slightly less compared to other bands. Thus, bands contributing the least to the spectral weight have the most Cl-p character. However, the same analysis for ex3 shows that mostly the topmost valence band and bottom-most conduction band contribute to the exciton spectral weight, while the other bands weakly participate in the process. This gives clear indication that in CrCl3 ex1 and ex2 are significantly localized in real space and are of Frenkel nature, while ex3 is closer to the Wannier–Mott limit. We also note the situation remains invariant whether we perform a similar analysis for bulk or ml cases.

Fig. 5: Spectral weight analysis in the band basis for the excitons in monolayer CrCl3.
figure 5

The spectral weight analysis for the three deepest lying exciton ex1 (a, d), ex2 (b, e) and ex3 (c, f) from left to right respectively. The size of the colored circles corresponds to the band contribution to the exciton spectral weight. Almost all the bands containing Cr-3dt2g↑ and eg↑ orbital characters contribute to ex1,2. Exciton spectral weight is almost uniformly spread across these bands in case of ex1,2. Spectral weight for ex3, which has lesser binding energy compared to ex1,2, becomes localized in band basis. Different colors are used to identify different bands.

Full size image

Now, we analyze the same across the series Cl → Br → I. We raise the spectral weight to the fourth power in all cases to identify variations in the band contribution to the spectral weights. We observe that for ex1 in ml-CrCl3, while almost all of six valence bands and four conduction bands contribute uniformly across the BZ, the situation is quite different for the ex1 in CrI3. In the case of ml-CrI3, we observe that mostly the two bottom-most conduction bands and one topmost valence band contribute to ex1 spectral weight (see Fig. 6), suggesting that the ex1 in CrI3 is significantly delocalized in nature compared to the other extreme of CrCl3. Also, even for the topmost valence band, we can identify the red circles becoming larger closer to the M-point and fainter away from that. A careful analysis of the orbital component of this topmost valence band shows27 that the Cr-d orbital character is most prominent at and around M-point while it becomes more I-p-like away from it. Altogether, CrI3 emerges as the extreme case of this series where ex1 is partially localized in momentum space, in strong contrast to CrCl3. A similar analysis for both bulk and ml for all cases are performed and the results are shown in the Supplemental Material.

Fig. 6: Spectral weight analysis in the band basis for the excitons in bulk CrCl3, CrBr3, CrI3.
figure 6

The spectral weight analysis for the deepest lying exciton ex1 in each case; (a, d) for CrCl3, (b, e) for CrBr3 and (c, f) for CrI3. The spectral weight is raised to the fourth power to identify variations in the band contribution to the spectral weight. In the direction of Cl → Br → I the number of bands that contribute to the spectral weight of ex1 decreases. Also the exciton spectral weight becomes more localized in band basis for X = I, compared to X = Cl, Br.

Full size image

Mimicking the role of absent vertex from the self-energy by modifying the Cr-d-X-p hybridization

To further explore the crucial role of Cr-d-X-p hybridization in determining the intensities and positions of these excitons, we apply a range of weak perturbations to the QS\(G\widehat{W}\) two-particle Hamiltonian that modifies the hybridization. Such a physical situation could be simulated within our calculations by either down/upshifting the X-p center of mass, downshifting/upshifting the Cr-d center of mass or by adding a Hubbard U to the Cr-d that shifts the Cr majority spin sector down and the minority spin sector up. We try these options on ml-CrBr3: shift the center of mass of Br-p up by 0.1 Ry, shift the Cr-d center of mass down/up by 0.1 Ry and add U = 1 eV to Cr-d. We refer to them respectively as Br + 0.1 Ry, Cr − 0.1 Ry, Cr + 0.1 Ry and Cr, U = 1 eV for the rest of the discussion. The bandgap changes in all cases, so does the hybridization between Cr-d and X-p. For Cr + 0.1 Ry (see Fig. 7e) the hybridization reduces slightly compared to the original unperturbed case (see Fig. 7b) and that leads to less intense exciton peaks (see the blue and black curves in Fig. 7a). Also as the atomic nature of the Cr-d becomes more prominent and it reflects in the exciton peaks getting weakly red-shifted (larger exciton-binding energy Eb) compared to the unperturbed scenario. The reverse happens with Br + 0.1 and for Cr − 0.1 Ry. In both the cases, the intensity of the ex1,2 peaks increase significantly (see Fig. 7a, red and purple curves) which is a direct consequence of larger hybridization between Cr-d and Br-p (see Fig. 7c, d) while the peak positions also get weakly blue-shifted leading to lesser Eb. However, with Cr, U = 1 eV the ex1 gets significantly blue-shifted to 1.35 eV (see Fig. 7a, magenta curve). Note that 1.35 eV is the exact position of the ex1 from the recent PL study11 on ml-CrBr3). In this scenario the Cr-d valence states get pushed down in energy27 leading to larger hybridization with Br-p (see Fig. 7f). This also suggests that the missing details of the vertex Γ, whether it is the dynamics in Γ or the vertex left out of the exact \({{\Sigma }}=iG\widehat{W}{{\Gamma }}\), will most likely lead to the same qualitative effect leading to the correction in the absolute positions of these deep-lying excitons. One primary effect of including Γ in Σ is to modify the relative center of masses of Cr-d and X-p while pushing the valence bands deeper in energy43. Note that our \({E}_{e{x}_{1}}\) estimation was ~0.5 eV too deep in both bulk and ml. With Cr, U = 1 eV we can correct \({E}_{e{x}_{1}}\) by ~0.5 eV in both bulk and ml. Hence, the discrepancy between our theory and experiment is related to the exact nature of the vertex and not the dimensionality of the material. It is also intuitive that this discrepancy is large (~0.5 eV) in X = Cl, Br where the systems are most atomic in nature and smaller (~0.2 eV) in X = I, where it is least atomic or most band-like. It is expected that the dynamics in vertex or a better vertex altogether (possibly from approaches that are more “exact” than these many-body perturbative approaches) is more relevant in the atomic scenario.

Fig. 7: Tunability of excitons in monolayer CrBr3 by modifying dp hybridization environment.
figure 7

QS\(G\widehat{W}\) results in different circumstances. a The Imϵxx is shown for different conditions from (b–f). b Unperturbed (original) DOS in ml-CrBr3. c Br + 0.1 Ry shifts the Br-p center of mass up by 0.1 Ry, (d) Cr − 0.1 Ry and (e) Cr + 0.1 Ry down/up shifts Cr-d the center of mass by 0.1 Ry and CrU = 1 eV adds U = 1 eV Cr-d. In cases with larger Cr-d and Br-p hybridization the excitons become more intense and get blue-shifted and the reverse happens for lesser hybridization. However, the position of ex1,2 changes dramatically for (f) CrU = 1 eV.

Full size image

Tuning the excitons using strain as a perturbation

To further verify the Frenkel character of the excitons, we apply moderate volume conserving strain ϵ on the monolayers of CrBr3 and CrI3. We observe that the positions of the excitons ex1,2, Eex remain invariant with both tensile and compressive strains in X = Br while it changes in X = I by roughly 100 meV for compressive strain ϵ = 7% (see Fig. 8). Weak changes with tensile ϵ in X = I can also be observed. This is consistent with our conclusions of excitons being most Frenkel-like in X = Cl, Br and more Wannier–Mott like in X = I.

Fig. 8: Tunability of excitons in monolayer CrBr3, CrI3 under strain.
figure 8

Volume conserving tensile and compressive strains ϵ are applied. Eex does not change for X = Br, while it changes by 100 meV for compressive strain of ϵ = 7% in X = I. Intensities of the peaks are multiplied by a constant factor of three in ml-CrBr3 to bring them to the same scale as ml-CrI3.

Full size image

Real-space structure of the Frenkel and the Wannier–Mott excitons

It becomes apparent from the analysis that CrCl3 is the most Frenkel-like, becoming more Wannier like in the sequence CrCl3 → CrBr3 → CrI3. We show in Fig. 9 that the ex1 is almost entirely localized within the unit cell for all ml-CrX3. Nevertheless, the fraction of the spectral weight shared with the ligand enhances in the direction Cl → Br → I. A large chunk of the spectral weight in CrI3 can be found on Iodine, consistent with the significant dp hybridization27 present there. However, the ex3 with lesser binding energy ~2 eV in CrCl3 is found to be delocalized over at least three unit cells. It is also interesting to note that excitons with similar binding energies across different materials (see Fig. 9c, d) can have very different real-space range, suggesting their fundamentally distinct “atomic” or “band-like” origins. The situation is dramatically different in MoS2 where the ex1 with Eb = 0.55 eV is delocalized over several nanometers. Our real-space depiction of the exciton is consistent with previous work37,44.

Fig. 9: Excitons in real space in CrX3 and MoS2 monolayers.
figure 9

The real-space range for the deepest lying exciton Eex1 is shown for CrX3. Excitons in CrCl3 (a) and CrBr3 (b) have similar extent, while they are slightly more delocalized in CrI3 (c) . As the binding energy reduces in CrCl3 for the exciton with Eb ~2 eV (d), it delocalizes over three unit cells. However, in ml-MoS2 with Eb = 0.55 eV (e), exciton is significantly more delocalized.

Full size image

We show that the lighter the halogen, the weaker the exciton intensity, making it even more challenging experimentally to observe them. Nevertheless, for a given material, as we look for excitons with lesser binding energies, for example ex3, in all cases, is the closest analog of Wannier–Mott exciton, although the real-space range of the excitons can still be significantly different from what is observed in LiF or MoS2 (see Fig. 9). The degree of “Wannier–Mott”-ness is proportional to the degree of hybridization between the Cr-d and X-p states, thereby supporting the picture of a “band-origin” for these excitons in CrX3. The band origin also suggests that it is, probably, possible to tweak their binding energies and intensities by applying shear, strain, magnetic field or simply by scanning across the periodic table looking for elements with varying degree of hybridization. However, as we show tensile or compressive strains lead to no changes in X = Cl, Br and finite changes in X = I to the exciton positions. Our analysis, further, puts CrCl3 and CrBr3 into one group where the exact details of the exciton position is sensitive to the proper treatment of vertex and less sensitive to substrate and spin–orbit coupling, while another group contains CrI3 where it is less sensitive to the exact treatment of the vertex and more sensitive to the substrate and spin–orbit coupling. Our study on the tunability of two-particle responses in CrI3 through substrate-screening45 supports our recent observations.

Our work establishes the fact that in real systems with significantly localized d-orbitals dp hybridization can be the primary symmetry-breaking mechanism that relaxes the Laporte rule, which forbids the “atomic” d − d transitions, as a fundamental principle of origin of these excitons. We analyze their spectral weights in both momentum and real space and show that this is definitely the case for bulk and monolayer Chromium tri-halides. While the deepest lying excitons are mostly localized on the Cr-d orbitals, they delocalize within the unit cell on the X-p orbitals as well. The degree of delocalization and real-space range of these excitons increase as the halogen atoms become heavier and contains more core states that are shallower compared to the Cr-d states. This suggests if CrF3 exists that could host the most localized Frenkel-like excitons, with the largest binding energies, from the entire series with, probably, the closest analog of what can be characterized as purely atomic d − d transition. We explicitly show that it is possible to modify both the intensities and positions of these excitons by applying weak perturbation to the Hamiltonian that changes the electronic gap and hybridization environment.

Methods

LDA, QSGW, and QS\(G\widehat{W}\) self-consistency

Single-particle calculations (LDA, and energy band calculations with the static quasiparticlized QSGW self-energy Σ0(k)) were performed on a 12 × 12 × 1 k-mesh while the (relatively smooth) dynamical self-energy Σ(k) was constructed using a 6 × 6 × 1 k-mesh and Σ0(k) extracted from it. For each iteration in the QSGW self-consistency cycle, the charge density was made self-consistent. The QSGW cycle was iterated until the RMS change in Σ0 reached 10−5 Ry. Thus the calculation was self-consistent in both Σ0(k) and the density. Numerous checks were made to verify that the self-consistent Σ0(k) was independent of starting point, for both QSGW and QS\(G\widehat{W}\) calculations; e.g., using LDA or Hartee–Fock self-energy as the initial self-energy for QSGW and using LDA or QSGW as the initial self-energy for QS\(G\widehat{W}\).

Momentum convergence for QS\(G\widehat{W}\) calculations and dielectric-response functions

We have checked the k-convergence of the one-particle and two-particle gap from QS\(G\widehat{W}\). We find that for CrX3 6 × 6 × 1 k-mesh is sufficient. However, in ml-MoS2 we need at least 16 × 16 × 1 k-mesh to achieve similar accuracy in convergence. The (dominant) RPA part of the polarizability is computed with the tetrahedron method, which helps to facilitate convergence. In the Supplemental Material, a thorough discussion is included for such differences in k-convergence of response functions in these two classes of materials. Our results are benchmarked against previous theoretical2,46,47,48 and experimental studies49,50,51,52. Our results for ml-MoS2, Eg of 2.51 eV, and Eb of 0.55 eV are in excellent agreement with experimental observations. The size of the two-particle Hamiltonian that we have diagonalized for CrX3 6 × 6 × 24 × 14 (nk × nk × Nv × Nc), i.e., 12,096. For nk = 9, it is 27,216.

We achieve these optical spectra in Fig. 2 using a uniform optical broadening of 2 milli-Hartree at all energies so that the peaks can be identified clearly. By contrast, in Fig. 1 an energy-dependent broadening that linearly varies from 2 milli-Hartree at the lowest energies to a maximum of 50 milli-Hartree at the highest energy (at 1 Rydberg) was used.