Abstract
Van der Waals heterostructures composed of multiple few layer crystals allow the engineering of novel materials with predefined properties. As an example, coupling graphene weakly to materials with large spin–orbit coupling (SOC) allows to engineer a sizeable SOC in graphene via proximity effects. The strength of the proximity effect depends on the overlap of the atomic orbitals, therefore, changing the interlayer distance via hydrostatic pressure can be utilized to enhance the interlayer coupling between the layers. In this work, we report measurements on a graphene/WSe2 heterostructure exposed to increasing hydrostatic pressure. A clear transition from weak localization to weak antilocalization is visible as the pressure increases, demonstrating the increase of induced SOC in graphene.
Similar content being viewed by others
Introduction
Graphene-based van der Waals (vdW) heterostructures became one of the most studied physical systems in material science in recent years, which led to the emergence of designer electronics1,2. Since the electrons are localized at the surface for a single layer of graphene by definition, their properties can be easily modified by combining it with other few layer crystals leading to remarkable changes in its band structure. A prominent example is the moiré effect caused by the rotation (and possible small lattice mismatch) of the graphene and the underlying other lattice. This led to the Hofstadter physics and formation of secondary charge neutrality points (CNPs) when graphene is placed on hexagonal boron nitride (hBN)3,4,5,6,7,8,9,10, whereas correlated phases including superconductivity correlated insulators or ferromagnetic states have been found if it is placed on another graphene sheet11,12,13,14. Graphene-based heterostructures are also promising building blocks for spintronic devices15,16,17.
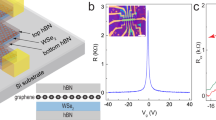
Although graphene is known to provide very long spin lifetimes18,19, the absence of spin–orbit coupling (SOC) also hinders electrical control and charge to spin conversion in it. However, a large SOC can be induced in graphene by proximity effect if placed on a transition metal dichalcogenide (TMDC) flake20,21,22 which can lead to topologically nontrivial states and the quantum spin Hall effect23. Recently, a wide range of experiments demonstrated the presence of proximity-induced SOC in various heterostructures by weak localization (WL), capacitance, or spin transport measurements, and it has been found that Rashba and valley–Zemann-like SOC is induced in graphene leading to a large spin relaxation anisotropy24,25,26,27,28,29,30,31,32,33,34,35. Since this enhancement of SOC originates from the hybridization of graphene’s π orbitals with the TMDC layer’s outer orbitals, the strength of the SOC depends strongly on the overlap of the orbital wavefunctions and, therefore, on the interlayer distance, which is determined by the vdW force. Compressing such a heterostructure by applying an external pressure (see Fig. 1a) is expected to increase the SOC, which can be captured by WL measurements, as shown by simulated magneto-conductivity curves in Fig. 1b21,36.
a Schematic side view of a hBN/graphene/WSe2 heterostructure in kerosene pressure transfer medium. Hydrostatic pressure reduces the distance d between the graphene and the WSe2 layers (among others), which leads to an enhancement of the proximity-induced SOC in graphene. b Simulated weak antilocalization curves using realistic parameters to demonstrate the potential effect of the application of ca. 2 GPa pressure on the heterostructure. The increased SOC leads to a more pronounced WAL peak in the magneto-conductivity curve. See Supplementary Note 1 for the simulation details.
In this work, we present experimental evidence of manipulation of the interlayer coupling and the proximity SOC in a graphene/WSe2 heterostructure using hydrostatic pressure. The pressure control adds another knob with which the electronic properties of 2D materials can be engineered, allowing to more robust proximity states or even engineer novel states of matter.
Results and discussion
General characterization of the device
The illustration of the studied device is shown in Fig. 1a, whereas an optical image is given in the inset of Fig. 2. It consists of a monolayer graphene, which is on top of a very thin (3 nm) WSe2 flake providing the SOC, and covered with a hBN flake to protect it from the kerosene pressure medium37 (see Fig. 1a). The device is also equipped with a top gate extending over the major part of the measured segment but it was grounded during the measurements. Another sample showing similar behavior is shown in Supplementary Fig. 1. Low-temperature (1.5 K) measurements have been carried out at four different hydrostatic pressure settings in increasing order (no pressure, 0.6 GPa, 1.2 GPa, 1.8 GPa). Each pressure change involved warming up the sample to room temperature, applying the pressure using a hydraulic press, clamping the pressure cell, and cooling the sample down again.
The curve minima, assumed to be the CNP, are shifted to Vg = 0 to maintain comparability of the curve shapes. The area considered for the comparison of the WAL signals, between 2.5 and 5.5 V, is highlighted by the gray background. Inset: Optical micrograph of the sample. Scale bar is 10 μm. The highlighted segment is measured in two-terminal measurements at 1.5 K for all pressures.
We characterized our devices by measuring the two-terminal conductance as a function of back gate voltage at each pressure, as shown in Fig. 2. The measured segment is highlighted in the inset. The CNP position was found at slightly different Vg back gate voltages in each case but remained between −5.2 and −0.6 V, which was corrected by shifting the curve minima to Vg = 0 for further use. The curves are quite similar in shape, with a minimum around the CNP. Using a simple parallel plate capacitor model for the estimation of the charge carrier density n(Vg), field effect mobility was calculated based on a linear fit on the two-terminal conductance. Electron mobility values were found between 11,000 and 24,000 cm2 V−1 s−1 without any systematic dependence on the applied pressure. A change in the scattering processes and the observed field effect mobility is not unusual in case of vdW heterostructures during subsequent cooldowns even without applied pressure and can be attributed to the rearrangement of scattering centers. Thus, we conclude that the sample conductance and quality are not significantly affected by the applied pressure.
WL measurements
Now we turn to low-field magneto-conductance measurements. WL is a low-temperature quantum correction to the magnetoconductance of diffusive samples and expected to show a conductance minimum (WL) or maximum (weak antilocalization, WAL) at zero field depending on the strength of SOC38.
We have recorded the two-terminal conductance curves as the B field was swept in a range of ±30 mT for several gate voltages, both in the up and down magnet ramping direction. At each gate voltage, we symmetrized the curves, then subtracted the zero-field conductance from the measured curve leading to 2D conductance maps ΔG(Vg, B). The zero-field conductance against the gate voltage for the no pressure case is plotted in Fig. 3a. The corresponding conductance map is shown in Fig. 3b, where a vertical dark gray line along B = 0 appears due to the correction method, and lighter gray tones on each side are a sign of positive magnetoconductance corresponding to WL. At higher magnetic fields, universal conductance fluctuations38 (UCF) of amplitude up to 0.4e2/h across the gate voltage axis are also visible on the map as saturated horizontal lines. To increase visibility of WAL signal, an averaging on a gate range of ±1.5 V was applied on the conductance, noted as ΔGavg(Vg, B). Cuts of ΔGavg at fixed Vg values are shown in Fig. 3c. All these cuts show a WL dip with slight changes in the curve shape as a function of the gate voltage. Here, the absence of a WAL peak suggests a weak SOC, which will be discussed later. This is in agreement with previous measurements on this device given in the Supplementary Material of ref. 31, which made this sample an ideal candidate for the pressure experiment.
a Zero-field conductance G(Vg, B = 0), used to extract D and τia, as detailed in the text. b 2D grayscale plot of the two-terminal conductance corrected by the zero-field conductance ΔG(Vg, B) = G(Vg, B) − G(Vg, B = 0). c Two-terminal magnetoconductance at fixed gate voltages marked in b with ±1.5 V averaging along the vertical axis to reduce the effect of UCF. The curves are shifted by 0.01 e2/h for clarity. At small magnetic fields (B < 5 mT), the well-formed conductance dip corresponds to weak localization (WL) effect that is present at all gate voltages, although the curve shape changes slightly. At higher fields (B > 5 mT), the influence of UCF leads to irregular line shapes and were not analyzed in the current work.
After having performed the above procedure for each pressure, we selected the curves at 4 ± 1.5 V, i.e., averaging the ΔG(Vg, B) curves between 2.5 and 5.5 V for all the pressures. We assume the characteristic times of the scattering processes do not change much across the gate range where the averaging is performed, while the contribution of UCF is reduced. The conductance was converted to conductivity for the extraction of scattering time scales by curve fitting. Background signal was also recorded simultaneously with the localization measurement and found to be constant, see Supplementary Fig. 2 for details.
Our main findings are presented in Fig. 4a, where the averaged magneto-conductivity Δσavg(Vg = 4 V, B) for all four pressures is plotted for low magnetic fields. The initial curve, at ambient pressure, shows a wide conductivity dip, which gets wider as the pressure increases to 0.6 GPa, and a sharp central peak appears at higher pressures. This transition of WL to WAL is a clear signature of the increasing proximity-induced SOC in the graphene layer. This tendency is robust for the entire gate voltage range as shown by the cuts at different gate voltages in Fig. 4b. See Supplementary Figs. 3 and 4 for the full comparison of all pressures at various gate voltages. Releasing the pressure again restores the WL dip, as presented in Supplementary Fig. 5.
a Comparison of averaged Δσavg(B) measurement curves for each pressure at 4 V. Clear signature of the WL→WAL evolution is visible. Solid blue lines for B > 0: fits using Eq. (1). b Two-terminal magnetoconductance for 1.8 GPa pressure at fixed gate voltages with ±1.5 V averaging to reduce the effect of UCF, similarly to 3c. The WAL peak observed in a is present at all gate values with changing amplitude but the width staying approximately the same. At higher fields (B > 5 mT) the influence of UCF is still dominant. c Summary plot of the fit values of τφ, τasy. The error bars represent uncertainty assessed by our method detailed in Supplementary Note 1. Decreasing τasy with increasing pressure indicates the presence of an increasing Rashba SOC and interlayer coupling strength between graphene and WSe2. d Fit values of τm. Due to the large uncertainty, the value of this parameter cannot be extracted. e λR parameter for each pressure, calculated using the previously extracted parameter values for τasy and τm. Calculated values based on the three-parameter formula (Eq. (1)) are plotted with orange, and values based on the five-parameter formula are plotted with green (see the Supplementary Note 1 for details). A clear growing tendency proves the enhancement of the proximity SOC induced by the WSe2 layer. The data points are slightly shifted horizontally to avoid overlapping error bars.
Curve fitting
To quantitatively demonstrate this transition, the data were fitted using the McCann–Falko WAL formula39
where Δσ(B) = σ(B) − σ(B = 0) is the correction to the magneto conductivity. We introduced the function \(F(x)={{\mathrm{ln}}}\,(x)+\psi (0.5+{x}^{-1})\) with ψ being the digamma function and h being the Planck’s constant. The rate \({\tau }_{B}^{-1}=4eDB/\hslash\) is associated to the magnetic field with D, the diffusion constant. τφ is the phase-breaking time, τasy is the scattering time due to SOC terms that are asymmetric upon z/-z inversion, and τsym is the corresponding time due to terms invariant under z/-z inversion. Using the previously calculated charge carrier density n(Vg), the Fermi velocity of graphene, and the Einstein relation, the diffusion constant and the momentum relaxation time can be extracted from the gate voltage curves and were found between D = 0.07–0.12 m2 s−1 and τm = 1.3–2.4 ⋅ 10−13 s for all pressure measurements without any systematic pressure dependence, but in correlation with the field effect mobility. Since τm is expected to be the shortest amongst the time scales, we set it as the lower bound for all fitting time parameters. Equation (1) is valid if the intervalley scattering time τiv is much shorter than the times corresponding to SOC, therefore the contribution of the effect of the charge carriers’ chiral nature can be neglected. We also performed fits with a more complex, five-parameter fitting formula including the τiv intervalley and τia intravalley scattering times as fitting parameters, which suggest that τiv is indeed at least an order of magnitude smaller than the other fitted time scales, supporting the validity of Eq. (1) (see Supplementary Note 1).
In Fig. 4a, fit curves are plotted using solid blue lines. The extracted fit parameters are summarized in Fig. 4c, d. A clear tendency of the reduction of τasy can be observed as its value decreases from 7.4 ⋅ 10−12 s to 2.7 ⋅ 10−12 s as the pressure increases to 1.8 GPa. This is a reduction by a factor of 2.7 and corresponds to an increasing SOC. This is the main proof to our initial expectation of increasing interlayer coupling. The phase-breaking time, τφ, also shows a moderately decreasing but fluctuating trend with pressure, obtaining values from 9.2 ⋅ 10−12 s to 5.5 ⋅ 10−12 s, staying well above τasy at all pressures. The reason for this decreasing tendency is unclear at the moment. The third fit parameter, τsym, obtains fit values that are much longer than τφ and the fit errors are more than an order of magnitude large (see Fig. 4d), which means that it has negligible effect on the magneto-conductance curve. Therefore, although there seems to be a decreasing trend in the lifetime, we cannot extract any reliable value for it at any pressure. Discussion on this result will be given later.
The spin relaxation times can be connected to band structure parameters via spin relaxation mechanisms. It has been established that two relevant spin orbit terms are formed in graphene/TMDC heterostructures. One of them is the Rashba term, described by the Hamiltonian HR = λR(κσxsy − σysx)40, which corresponds to the breaking of the lateral mirror symmetry due to the difference of the hBN and TMDC neighboring layers to the graphene sheet. Its strength is set by the λR parameter, κ = ±1 for the K and K′ valleys, the Pauli matrices σ are acting on the lattice pseudospin, and kx, ky are the electron wave vector components measured from the K (K′) points. This term leads to relaxation processes that are contained in τasy via the Dyakonov–Perel mechanism, from which the Rashba parameter can be expressed as \({\lambda }_{{{\mbox{R}}}}=\frac{\hslash }{2}\sqrt{{\tau }_{{{\mbox{m}}}}^{-1}{\tau }_{{{\mbox{asy}}}\,}^{-1}}\)41.
The increasing scattering rates lead to an increase in the Rashba parameter, which clearly demonstrates that we were able to tune the strength of the induced SOC. The values are summarized in Fig. 4e, shown by the orange curve. We have also plotted the value of the Rashba parameter from the five-parameter fitting formula in green (see Supplementary Note 1), which is in agreement with the values from the simplified formula within the error limits.
The second dominant spin orbit term in these systems is the HVZ = λVZκσ0sz valley–Zeeman term, where λVZ characterizes the coupling strength. This term corresponds to an effective Zeeman magnetic field which is opposite in the two valleys due to inversion symmetry breaking, but still preserving time reversal symmetry. It leads to relaxation contained in the τsym via a modified Dyakonov–Perel mechanism, where the intervalley scattering time, τiv, enters instead of the momentum scattering time \({\lambda }_{{{\mbox{vz}}}}=\frac{\hslash }{2}\sqrt{{\tau }_{{{\mbox{iv}}}}^{-1}{\tau }_{{{\mbox{sym}}}\,}^{-1}}.\)
The strength of the valley–Zeeman coupling cannot be extracted reliably in our experiments due to the uncertainty in τsym. The mean values from the fit show a slightly increasing trend and would give 4 and 23 eV for the lowest and highest pressure, respectively, but even taking the smallest obtained values from τsym, we arrive at values between 140 and 440 eV.
In order to quantify changes in the Rashba parameter and to compare it to expectations, we have performed ab initio calculations following our previous results in ref. 20,21. Using a structural supercell model of 4 × 4 graphene and 3 × 3 WSe2 with relaxed lateral atomic positions, 5%/GPa compressibility for the layer distance between the graphene and WSe2 layers was found. The applied 1.8 GPa pressure induces 9% compression in the z direction that leads to an increment of the calculated Rashba energy from 600 eV to 1.8 meV and of the calculated valley–Zeeman energy from 1.2 to 3.0 meV.
As plotted in Fig. 4e, the value of the Rashba energy λR increases from 0.3 to 0.5 meV, which is in the order of magnitude of the expected values, although slightly lower than them. The values of the valley–Zeeman energy are much smaller than expected theoretically.
Several reasons might be behind these low SOC values relative to the theoretical expectations originating from the imperfection of the stacking process. One possibility is that the interfaces are not clean enough and some contamination is trapped in-between, see Supplementary Fig. 8, which would lower the strength of the SOC. Another difference from other samples31 might come from the relative orientation of the graphene and the WSe2. It has been theoretically found42,43 that the rotation angle strongly modulates the strength of the SOC and for certain angles the SOC almost disappears. Since we did not control the twist angles between the layers during fabrication, they may have aligned such a way that it would lead to reduced SOC. The rotation angle affects the Rashba and the valley–Zeeman coupling in a different way, which can explain why we see stronger suppression for the λVZ than for λR, and why the former deviated between measured and simulated values. Finally, we note that the strength of SOC obtained from these formulas might also depend on how well the UCF is removed during averaging. This can be seen in Fig. 4b, where the different gate values lead to slightly different magneto-conductance trend. We stress here that although the absolute value of the extracted parameters has to be taken with care, the tendency visible in Fig. 4a clearly shows that the pressure indeed leads to an increase of the SOC. We neither expect that the twist angle is modulated by the applied pressure44 nor the functional form of the angle dependence is modified by it, only the overall strength of the SOC is affected.
In conclusion, we studied the effect of hydrostatic pressure on WL signal in graphene/TMDC heterostructure. We demonstrated the enhancement of the proximity-induced SOC using hydrostatic pressure. Our analysis of the measured signals supports an increasing SOC and is in qualitative agreement with theoretical expectations. The strength of SOC is an important parameter in graphene spintronics, since it determines charge to spin conversion efficiencies and also plays a central role in graphene–TMDC optoelectronic devices20. Our work also points out that hydrostatic pressure can be generally used to change the interlayer distance up to a remarkable 10%, which provides an experimental knob to boost proximity effects in vdW heterostructures, e.g., exchange interaction induced into graphene45,46,47,48 or into TDMCs49,50, furthermore, a strong proximity effect on correlated magic angle twistronics devices51,52, or to stabilize fragile states such as the topological insulator phase in graphene–TDMC heterostructures33.
Methods
Device fabrication
The heterostructure is built on a Si/SiO2 substrate using the dry stacking assembly method53, where the heavily doped silicon layer was used as a global back gate. The WSe2 crystal is from HQ Graphene, whereas the hBN crystal was grown at the National Institute for Materials Science, Japan. It is then shaped into a Hall bar and contacted using 1D Cr/Au electrodes54 using electron beam lithography and reactive ion etching (see Fig. 2 inset). The total length of the graphene segment was L = 8.3 m and the width was W = 1.1 m.
Sample preparation
The wafer carrying the device was cut tightly and bonded on a special high-pressure sample holder, then placed in kerosene environment in a piston-cylinder hydrostatic pressure cell. The setup is designed to overcome the technical difficulties of electronic measurements of nanocircuits in a hostile environment37. Measurements were carried out by standard lock-in technique at f = 177 Hz with an AC bias voltage VAC = 100 V and an external low-noise current amplifier.
Data availability
The data presented in this work are available at https://doi.org/10.5281/zenodo.4671804.
References
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419–425 (2013).
Giustino, F. et al. The 2021 quantum materials roadmap. J. Phys. Mater. 3, 042006 (2021).
Dean, C. R. et al. Hofstadter’s butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 497, 598 (2013).
Ponomarenko, L. A. et al. Cloning of Dirac fermions in graphene superlattices. Nature 497, 594–597 (2013).
Hunt, B. et al. Massive Dirac fermions and Hofstadter butterfly in a van der Waals heterostructure. Science 340, 1427 (2013).
Krishna Kumar, R. et al. High-temperature quantum oscillations caused by recurring Bloch states in graphene superlattices. Science 357, 181 (2017).
Krishna Kumar, R. et al. High-order fractal states in graphene superlattices. Proc. Natl Acad. Sci. USA 115, 5135 (2018).
Wang, L. et al. New generation of moiré superlattices in doubly aligned hBN/graphene/hBN heterostructures. Nano Lett. 19, 2371–2376 (2019).
Wang, Z. et al. Composite super-moiré lattices in double-aligned graphene heterostructures. Sci. Adv. 5, eaay8897 (2019).
Yankowitz, M., Ma, Q., Jarillo-Herrero, P. & LeRoy, B. J. Van der Waals heterostructures combining graphene and hexagonal boron nitride. Nat. Rev. Phys. 1, 112–125 (2019).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43 (2018).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80 (2018).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Han, W., Kawakami, R. K., Gmitra, M. & Fabian, J. Graphene spintronics. Nat. Nano 9, 794–807 (2014).
Avsar, A. et al. Colloquium: spintronics in graphene and other two-dimensional materials. Rev. Mod. Phys. 92, 021003 (2020).
Hu, G. & Xiang, B. Recent advances in two-dimensional spintronics. Nanoscale Res. Lett. 15, 226 (2020).
Kamalakar, M. V., Groenveld, C., Dankert, A. & Dash, S. P. Long distance spin communication in chemical vapour deposited graphene. Nat. Commun. 6, 6766 (2015).
Drögeler, M. et al. Spin lifetimes exceeding 12 ns in graphene nonlocal spin valve devices. Nano Lett. 16, 3533–3539 (2016).
Gmitra, M. & Fabian, J. Graphene on transition-metal dichalcogenides: a platform for proximity spin-orbit physics and optospintronics. Phys. Rev. B 92, 155403 (2015).
Gmitra, M., Kochan, D., Högl, P. & Fabian, J. Trivial and inverted Dirac bands and the emergence of quantum spin Hall states in graphene on transition-metal dichalcogenides. Phys. Rev. B 93, 155104 (2016).
Garcia, J. H., Cummings, A. W. & Roche, S. Spin Hall effect and weak antilocalization in graphene/transition metal dichalcogenide heterostructures. Nano Lett. 17, 5078–5083 (2017).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Avsar, A. et al. Spin-orbit proximity effect in graphene. Nat. Commun. 5, 4875 (2014).
Wang, Z. et al. Strong interface-induced spin-orbit interaction in graphene on WS2. Nat. Commun. 6, 8339 (2015).
Wang, Z. et al. Origin and magnitude of ‘designer’ spin-orbit interaction in graphene on semiconducting transition metal dichalcogenides. Phys. Rev. X 6, 041020 (2016).
Yang, B. et al. Tunable spin-orbit coupling and symmetry-protected edge states in graphene/WS2. 2D Mater. 3, 031012 (2016).
Ghiasi, T. S., Ingla-Aynés, J., Kaverzin, A. A. & van Wees, B. J. Large proximity-induced spin lifetime anisotropy in transition-metal dichalcogenide/graphene heterostructures. Nano Lett. 17, 7528–7532 (2017).
Yang, B. et al. Strong electron-hole symmetric Rashba spin-orbit coupling in graphene/monolayer transition metal dichalcogenide heterostructures. Phys. Rev. B 96, 041409 (2017).
Benítez, L. A. et al. Strongly anisotropic spin relaxation in graphene-transition metal dichalcogenide heterostructures at room temperature. Nat. Phys. 14, 303–308 (2018).
Zihlmann, S. et al. Large spin relaxation anisotropy and valley-Zeeman spin-orbit coupling in wse2/graphene/h-BN heterostructures. Phys. Rev. B 97, 075434 (2018).
Ringer, S. et al. Measuring anisotropic spin relaxation in graphene. Phys. Rev. B 97, 205439 (2018).
Island, J. O. et al. Spin-orbit-driven band inversion in bilayer graphene by the van der Waals proximity effect. Nature 571, 85–89 (2019).
Wakamura, T. et al. Spin-orbit interaction induced in graphene by transition metal dichalcogenides. Phys. Rev. B 99, 245402 (2019).
Amann, J. et al. Gate-tunable spin-orbit-coupling in bilayer graphene-WSe2-heterostructures. Preprint at https://arxiv.org/abs/2012.05718 (2020).
Carr, S., Fang, S., Jarillo-Herrero, P. & Kaxiras, E. Pressure dependence of the magic twist angle in graphene superlattices. Phys. Rev. B 98, 085144 (2018).
Fülöp, B. et al. New method of transport measurements on van der Waals heterostructures under pressure. J. Appl. Phys., Am. Inst. Phy. 130, 064303 (2021).
Ihn, T. Electronic Quantum Transport in Mesoscopic Semiconductor Structures (Springer-Verlag, 2004).
McCann, E. & Fal’ko, V. I. z→−z symmetry of spin-orbit coupling and weak localization in graphene. Phys. Rev. Lett. 108, 166606 (2012).
Konschuh, S., Gmitra, M. & Fabian, J. Tight-binding theory of the spin-orbit coupling in graphene. Phys. Rev. B 82, 245412 (2010).
Cummings, A. W., Garcia, J. H., Fabian, J. & Roche, S. Giant spin lifetime anisotropy in graphene induced by proximity effects. Phys. Rev. Lett. 119, 206601 (2017).
Li, Y. & Koshino, M. Twist-angle dependence of the proximity spin-orbit coupling in graphene on transition-metal dichalcogenides. Phys. Rev. B 99, 075438 (2019).
David, A., Rakyta, P., Kormányos, A. & Burkard, G. Induced spin-orbit coupling in twisted graphene–transition metal dichalcogenide heterobilayers: twistronics meets spintronics. Phys. Rev. B 100, 085412 (2019).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059 (2019).
Ghazaryan, D. et al. Magnon-assisted tunnelling in van der Waals heterostructures based on CrBr3. Nat. Electr. 1, 344–349 (2018).
Wang, Z., Tang, C., Sachs, R., Barlas, Y. & Shi, J. Proximity-induced ferromagnetism in graphene revealed by the anomalous Hall effect. Phys. Rev. Lett. 114, 016603 (2015).
Karpiak, B. et al. Magnetic proximity in a van der Waals heterostructure of magnetic insulator and graphene. 2D Mater. 7, 015026 (2019).
Ghiasi, T. S. et al. Electrical and thermal generation of spin currents by magnetic bilayer graphene. Nat. Nanotechnol. https://doi.org/10.1038/s41565-021-00887-3 (2021).
Zollner, K., Faria Junior, P. E. & Fabian, J. Giant proximity exchange and valley splitting in transition metal dichalcogenide/hBN/(Co, Ni) heterostructures. Phys. Rev. B 101, 085112 (2020).
Zhong, D. et al. Layer-resolved magnetic proximity effect in van der Waals heterostructures. Nat. Nanotechnol. 15, 187–191 (2020).
Arora, H. S. et al. Superconductivity in metallic twisted bilayer graphene stabilized by WSe2. Nature 583, 379–384 (2020).
Lin, J.-X. et al. Spin-orbit driven ferromagnetism at half moir\’e filling in magic-angle twisted bilayer. Science, in press (2021).
Zomer, P. J., Guimarães, M. H. D., Brant, J. C., Tombros, N. & van Wees, B. J. Fast pick up technique for high quality heterostructures of bilayer graphene and hexagonal boron nitride. Appl. Phys. Lett. 105, 013101 (2014).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Acknowledgements
This work was supported by the Topograph FlagERA network (OTKA NN-127903), the OTKA FK-123894 and PD-134758 grants, the Swiss Nanoscience Institute, the ERC project Top-Supra (787414), the Swiss National Science Foundation, the Swiss NCCR QSIT, the Ministry of Innovation and Technology, and the National Research, Development and Innovation Office within the Quantum Information National Laboratory of Hungary and by the Quantum Technology National Excellence Program (Project Nr. 2017-1.2.1-NKP-2017-00001), by VEKOP-2.3.3-15-2017-00015, by SuperTop QuantERA network, and by the FET Open AndQC network. This article is based upon work from COST Action CA16218 Nanocohybri, supported by COST (European Cooperation in Science and Technology)—www.cost.eu. P.M. and E.T. received funding from Bolyai Fellowship. M.G. acknowledges Scientific Grant Agency of the Ministry of Education of the Slovak Republic under the contract no. VEGA 1/0105/20. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan, Grant Number JPMXP0112101001, JSPS KAKENHI Grant Numbers JP20H00354 and the CREST(JPMJCR15F3), JST. The authors thank Andor Kormányos, András Pályi, and Péter Boross for fruitful discussions and Márton Hajdú and Ferenc Fülöp’s team for their technical support.
Author information
Authors and Affiliations
Contributions
S.Z., M.K. and P.M. fabricated the devices. Measurements were performed by B.F. and A.M. with the help of E.T. and B.S. Author B.F. did the data analysis. M.G. did the theoretical calculation. B.F., P.M. and C.S. wrote the paper. All authors discussed the results and worked on the manuscript. K.W. and T.T. grew the hBN crystals. The project was guided by S.C., P.M., C.S. and J.F.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fülöp, B., Márffy, A., Zihlmann, S. et al. Boosting proximity spin–orbit coupling in graphene/WSe2 heterostructures via hydrostatic pressure. npj 2D Mater Appl 5, 82 (2021). https://doi.org/10.1038/s41699-021-00262-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-021-00262-9
This article is cited by
-
Ballistic transport spectroscopy of spin-orbit-coupled bands in monolayer graphene on WSe2
Nature Communications (2023)
-
Spin–orbit coupling in buckled monolayer nitrogene
Scientific Reports (2022)