Introduction

Electrical contacts between metals and semiconductors are ubiquitous in modern electronic and optoelectronic devices. An interfacial potential barrier, known as the Schottky barrier (SB), is commonly formed at the metal/semiconductor interface. In electronics and optoelectronics applications, the presence of a sizable Schottky barrier height (SBH), typically larger than a few kBT, can severely impede the charge injection efficiency1. As the SBH is intimately linked to the contact resistance at the metal/semiconductor contact2,3, reducing the SBH at the metal/semiconductor contact has become one of the key challenges towards energy-efficient and high-speed semiconductor devices.

In a metal/semiconductor contact, SBH arises from the mismatch between the metal work function (WM) and the semiconductor electron affinity Eea (n-type Schottky contact) or ionization potential Eip (p-type Schottky contact). The SBH across a metal/semiconductor contact can be phenomenologically captured by the modified Schottky–Mott (SM) rule4,5,6,7,

$${{{\Phi }}}_{{{\mbox{Be}}}}={S}_{{{\mbox{e}}}}({W}_{{{\mbox{M}}}}-{E}_{{{\mbox{ea}}}})+{c}_{{{\mbox{e}}}}$$
(1)
$${{{\Phi }}}_{{{\mbox{Bh}}}}={S}_{{{\mbox{h}}}}({E}_{{{\mbox{ip}}}}-{W}_{{{\mbox{M}}}})+{c}_{{{\mbox{h}}}},$$
(2)

where the subscript “e” and “h” denote n-and p-type contacts, respectively, ce(h) is a material-and contact-dependent term7, and ΦBe and ΦBh is the electron-type and hole-type SBH, respectively. Here, the slope parameter, Se(h), is defined as

$${S}_{{{\mbox{e}}}({{\mbox{h}}})}\equiv \left|\frac{d{{{\Phi }}}_{{{\mbox{Be}}}({{\mbox{h}}})}}{d{W}_{{{\mbox{M}}}}}\right|$$
(3)

which is an important phenomenological parameter widely used in characterizing the deviation of the SBH from the ideal SM limit (S = 1). In realistic metal/semiconductor contacts, S ≪ 1 due to the presence of multiple nonideal factors, such as the formation of metal-induced gap states, defect-induced gap states, mid-gap states, and interface dipole, as well as the modifications of the electronic band structures of the semiconductor when contacted by metals6,7. In this case, the SBH is pinned to a narrow range of value— an adverse effect commonly known as the Fermi level pinning (FLP).

In the few-atom-thick limit, two-dimensional (2D) semiconductors8, such as MoS2 and WS29, continue to be plagued by FLP10. Although 2D semiconductors and their van der Waals (VDW) heterostructures has shown great promises in low-power electronics11, optoelectronics12, and neuromorphic applications13, the lack of wide-range tunable SBH—commonplace in most 2D semiconductors—has severely impeded the development of high-performance nanodevices. Particularly, the metallization of a 2D semiconductor by the contacting metal often substantially alters the electronic structures of the heterostructure via the generation of mid-gap states14,15, causing strong FLP effect that leads to a poor SBH tunability15. For the vast majority of 2D semiconductors, S is typically less than 0.4 as predicted by density functional theory (DFT) calculations, and are even lower in experimental measurements due to the inevitable presence of defects at the contact interface. To resurrect a wide-range tunable SBH in 2D semiconductors, atomically sharp VDW metal/2D-semiconductor electrical contacts have been proposed16. Such VDW-type contacts harness the weak VDW interfacial coupling to reduce the metal/semiconductor interactions, yielding an S ≈ 1 that approaches the ideal SM limit17,18,19. However, as VDW-type contact often involves complex fabrication techniques, a 2D semiconductor class that can inherently achieve substantial Fermi level unpinning without necessarily relying on the VDW contact paradigm remains elusive thus far.

In this work, we perform a first-principle DFT investigation to study the metal contact properties in the recently discovered synthetic 2D monolayers, MoSi2N4 and WSi2N420,21. We focus on face-type contact1 as it is widely employed in both the experimental design of 2D nanodevices18,19,22,23,24,25,26 and the computational contact simulation studies15,17,27,28,29. The recent demonstrations of ultralow contact resistance and the high on-state current in face-contacted 2D semiconductor18,19,22 also reveal the technological importance of face-type contact towards the development of high-performance 2D nanodevices30. We show that, in contrary to the common knowledge that 2D semiconductors are prone to strong FLP, MoSi2N4, and WSi2N4 monolayers exhibit strongly suppressed FLP and excellent SBH tunability without relying on the VDW-type contact engineering. The SBH is widely tunable in MoSi2N4 and WSi2N4 monolayers, reaching an exceptionally high slope parameter of S = 0.69 and S = 0.77, respectively—a value much larger than other commonly studied 2D semiconductors. The FLP suppression originates from the unusual morphology and the electronic properties of MoSi2N4 and WSi2N4 monolayers, in which the semiconducting states residing in Mo–N or W–N inner core-layer are protected by the outlying Si–N atomic layers—an intriguing mechanism not found in other classes of 2D semiconductors. Our results reveal MoSi2N4 and WSi2N4 monolayer as an unusual 2D semiconductor class with built-in atomic layer protection, thus opening up an alternative and complementary route to the VDW contact paradigm towards efficient SBH tuning and high-performance electrical contact engineering.

Results

Electronic properties of MoSi2N4 and WSi2N4 metal contacts

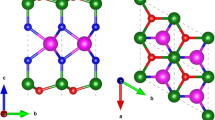
The 2D monolayers of MoSi2N4 and WSi2N4 blue [see Fig. 1a, b for the lattice structures of MoSi2N4 and WSi2N4] belong to the family of MA2Z4 synthetic 2D layered materials with no known 3D parent materials (M = early transition metal, A = Si or Ge, Z = N, P, or As). The MA2Z4 2D material family covers a wide variety of semiconducting, metallic, insulating, and magnetic phases, offering an exciting platform for the exploration of 2D semiconductor physics and device applications31,32,33,34,35. Structurally, MoSi2N4 (WSi2N4) monolayer is composed of a Mo–N (W–N) monolayer sandwiched by two Si–N layers. Electronically, MoSi2N4 and WSi2N4 monolayers are indirect band gap semiconductors with band gap values of 1.73 and 2.06 eV, respectively [Fig. 1c, d], and exhibit excellent structural stability and mechanical strength20.

Fig. 1: Lattice structures, energy band structures, and S parameters of MoSi2N4 and WSi2N4 monolayers.
figure 1

a Top and side view of MoSi2N4 monolayer, b same as a for WSi2N4 monolayer, c and d electronic band structures of isolated MoSi2N4 and WSi2N4 monolayer, respectively. e The slope parameter S versus the metal work function range (ΔWM) of a large variety of 2D semiconductors, showing exceptionally large S for MoSi2N4 and WSi2N4. Included are the DFT simulations of MoS2 [face contact14,15,27,41 and edge contact27], WS227,39, WSe240, MoSe227, MoTe227, black phosphorus42,43,44,45, blue phosphorus45, antimonene46, tellurene47, InSe [3D metal contact36 and 2D metal VDW contact37], ReS238, and the experimental results of MoS248,49 and SnS250. The notations “2L” and “3L” denote bilayer and trilayer, respectively. The MoSi2N4 and WSi2N4 are highlighted by the dashed box.

Full size image

We perform first-principles DFT simulations to model the heterostructure composed of MoSi2N4 and WSi2N4 monolayers contacted by a large variety of metals (3D metals Sc, In, Ti, Ag, Cu, Ni, Au, Pd, Pt; 2D semimetal graphene; and 2D metal NbS2 monolayer) with work function values ranging from 3.3 to 6.0 eV (see Method section for the DFT simulation procedures). Comparing with a large variety of previously reported 2D semiconductors14,15,27,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51 [Fig. 1e], our calculation reveals an exceptionally large S-parameter for MoSi2N4 and WSi2N4 of S = 0.69 and S = 0.77, respectively, which spans over a large contacting metal work function range of ΔWM = 2.7 eV.

In general, the metal contacts to MoSi2N4 and WSi2N4 cover a large variety of contact types, including n-type Schottky contact, p-type Schottky contact, and Ohmic contact with zero SBH. The interlayer distance between the metal and 2D monolayers is less than 3 Å for Cu, Pd, Ti, and Ni (see Supplementary Tables 1 and 2), suggesting the prevalence of non-VDW-type metal contacts. In the following, we shall take Au and Ti metal contacts as illustrative examples of Schottky (Fig. 2) and Ohmic contacts (Fig. 3), respectively (see Supplementary Fig. 1 for the relaxed lattice structures of all metal contacts calculated in this work). The lattice structures of the Au and Ti contacts to MoSi2N4 and WSi2N4 monolayers are shown in Figs. 2a and 3a, respectively.

Fig. 2: Schottky contacts of Au/MoSi2N4 and Au/WSi2N4 - Structural and electronic properties.
figure 2

a The contact is composed of six layers of Au atoms contacting the MoSi2N4 monolayer. The interlayer distance is 3.13 Å and the minimum distance between Au and N atoms is 3.55 Å. b The projected electronic band structure and the partial density of states of Au/MoSi2N4 contact. The panels in c from left to right, show the spatial charge density distribution of VBM states, mid-gap states between VBM and CBM, and the CBM states, the differential charge density, and the electrostatic potential profile across the heterostructures. d–f Same as a, b, and c, respectively, for Au/WSi2N4 contact. The interlayer distance is 3.13 Å and the minimum distance between Au and N atoms is 3.54 Å.

Full size image
Fig. 3: Ohmic contacts of Ti/MoSi2N4 and Ti/WSi2N4—structural and electronic properties.
figure 3

a The contact is composed of six layers of Ti atoms contacting the MoSi2N4 monolayer. The interlayer distance is 1.75 Å and the minimum distance between Ti and N atoms is 2.43 Å. b The projected electronic band structure and the partial density of states of Ti/MoSi2N4 contact. The panels in c from left to right, show the spatial charge density distribution of VBM states, mid-gap states between VBM and CBM, and the CBM states, the differential charge density, and the electrostatic potential profile across the heterostructures. d–f Same as a, b, and c, respectively, for Ti/WSi2N4 contact. The interlayer distance is 1.78 Å and the minimum distance between Ti and N atoms is 2.45 Å.

Full size image

A closer inspection of the electronic band structures of the metal/MoSi2N4 and metal/WSi2N4 reveals intriguing behaviors. The metal/semiconductor heterostructures are nearly free of mid-gap states for all metals as revealed in the projected band structures and the partial density of states (PDOS) [Fig. 2b, e for Au Schottky contacts and Fig. 3b, e for Ti Ohmic contact, see also Supplementary Fig. 2 for the projected band structures and PDOS of other metal contacts]. By projecting the 2D semiconductor electronic states onto the band structures, we find that the semiconducting bands, particularly the electronic states around the valence band maximum (VBM) and the conduction band minimum (CBM), remain intact in all metal contacts, suggesting the near absence of mid-gap states within the semiconductor band gap. For Ti contact, despite being a close contact type with an exceedingly small interlayer distance of 1.75 and 1.78 Å, mid-gap states remain nearly absent [see PDOS in Fig. 3b, e], which is in stark contrast to metal-contacted MoS2 where a large abundance of mid-gap states localizing in the Mo sites are created15,52.

We further calculate the spatial charge density distribution around the VBM and the CBM, as well as the states between the VBM and the CBM. Intriguingly, the semiconducting electronic states are embedded deeply within inner Mo–N [Figs. 2c and 3c] and W–N core layer [Figs. 2f and 3f], while the mid-gap states between the VBM and CBM are mostly located in the metals and sparsely distributed in the outlying Si–N layers. Such metal-induced mid-gap states decay rapidly without penetrating into the semiconducting inner core layer, thus leading to a much-weakened FLP. We also calculate the differential charge density (Δρ) which reveals a significant charge redistribution across the metal/semiconductor contact interface [Figs. 2c, f and 3c, f]. As Δρ across the contact interface is asymmetrical, the formation of interface dipole is expected to modify the S parameter from the ideal SM limit (see Supplementary Fig. 4 for the calculated Δρ of other metal contacts).

The effective electrostatic potential profile, Veff, across the metal/semiconductor contact is shown in the left-most panels of Fig. 2c, f for Au contact, and Fig. 3c, f for Ti contact. For contacts with Veff higher than the Fermi level at the metal/semiconductor interface, the Veff forms an interfacial tunneling potential barrier (denoted as ΦTB in Figs. 2 and 3), which significantly impedes the charge injection efficiency. In the case of Au contact, the presence of a sizable barrier of ΦTB ≈ 3.13 eV [Fig. 2c, f] reveals a much-reduced electron transmission across the metal/semiconductor contact. In contrast, the absence of ΦTB in the case of Ti contact [Fig. 3c, f] reveals the potential of Ti as an efficient electrode to MoSi2N4 and WSi2N4 with a large electron transmission probability. The ΦTB and the corresponding electron transmission probability of various metal contacts to MoSi2N4 and WSi2N4 will be discussed in detail below.

The absence of mid-gap states in the inner core layer and the finite charge transfer at the outlying Si–N layers reveals that the metal/semiconductor interaction affects mostly the outlying Si–N layers, predominantly via charge redistribution, without penetrating semiconducting Mo–N and W–N inner cores. Here the Si–N layer serves as an encapsulating layer and plays a vital role in preserving the semiconducting characteristics of MoSi2N4 and WSi2N4 monolayers. To verify the protective effect of Si–N layers53, we simulate a close contact type of Au/MoSi2N4 and Au/WSi2N4 heterostructures by forcing the interlayer distance to 1.5 Å, compared to the fully relaxed value of about 3.13 Å (see Supplementary Fig. 3). The semiconducting band structures are well-preserved at this close-contact limit, thus confirming the robustness of the semiconducting states residing in the MoSi2N4 and WSi2N4 monolayers and the resilience against mid-gap states formation. Such unusual behavior, enabled by the septuple-layered morphology of MoSi2N4 and WSi2N4 monolayer, is not found in other commonly studied 2D semiconductors, such as transition metal dichalcogenides (TMDCs) and black phosphorus, in which an external insertion layer is often required to unpin the Fermi level54,55,56. We further perform a comparison with monolayer MoS2 by calculating the charge density distribution39 and the electronic band structures of Sc/MoSi2N4 and the Sc/MoS2 contacts in Fig. 4. The charge density plots in Fig. 4a, c shows the presence of a large amount of electrons from Sc atoms overlapping strongly with the MoS2 layer [Fig. 4c] while the MoSi2N4 layer remains well-isolated from the electrons of Sc atoms [Fig. 4a]. Such electron overlap in Sc/MoS2 directly leads to strong metal-semiconductor hybridization as evident from the band structure and the PDOS plot in Fig. 4d, which is in strong contrast to the case of Sc/MoSi2N4 in Fig. 4b where the electronic states around CBM and VBM remain intact.

Fig. 4: Comparing Sc contacts to MoSi2N4 MoS2.
figure 4

a Contour plots of total electron distribution of Sc/MoSi2N4. b Band structure and projected density of states of Sc/MoSi2N4. c, d Same as b and c, respectively, but for Sc/MoS2.

Full size image

As the CBM and VBM electronic states contribute dominantly to the carrier transport, the suppression of FLP due to the atomic-layer protection as discussed above can also be understood as the consequence of having a transport channel that is spatially well-separated from the influence of the contacting metal atoms. In the case of MoS2—a triple-layered structure which is morphologically much thinner than the septuple-layered MoSi2N4, the transport channel residing around the Mo atoms is in closer proximity with the contacting metal and hence the presence of stronger hybridization leads to a more severe FLP effect.

Interfacial tunneling potential barrier and Schottky barrier

As discussed above, the formation of a tunneling potential barrier, ΦTB, at the metal/semiconductor gap impedes the charge injection efficiency52. The ΦTB and the barrier width, dTB can be determined from the effective electrostatic potential across the metal/semiconductor interface (see Supplementary Fig. 5). For both MoSi2N4 and WSi2N4 monolayers, ΦTB ranges between 2.8 and over 5.1 eV, and the thickness dTB ranges between 1.1 and 2 Å (see Supplementary Tables 1 and 2). The corresponding electron tunneling probability across the interface can be then calculated as,

$${{{\mathcal{T}}}}({{{\Phi }}}_{{{\mbox{TB}}}},{d}_{{{\mbox{TB}}}})=\exp \left(-\frac{4\pi \sqrt{2{m}_{e}{{{\Phi }}}_{{{\mbox{TB}}}}}{d}_{{{\mbox{TB}}}}}{\hslash }\right),$$
(4)

where me is the free electron mass. The \({{{\mathcal{T}}}}({{{\Phi }}}_{{{\mbox{TB}}}},{d}_{{{\mbox{TB}}}})\) calculated via Eq. (4) for various metal contacts are shown in Fig. 5a. For Sc, Ti, and Ni, the tunneling probability reaches 100% as ΦTB = 0. Particularly for Sc and Ti, both ΦTB and ΦB are zero in both MoSi2N4 and WSi2N4 monolayers—an indication of good Ohmic contacts with high charge injection efficiency. In contrast, the VDW-type contacts, such as graphene and NbS2 with interlayer distances greater than 3 Å, exhibit very low \({{{\mathcal{T}}}}\) of less than 2%, which suggests a low electron transparency in such VDW-type interfaces.

Fig. 5: \({{{\mathcal{T}}}}\) and SBH of the contact heterostructures.
figure 5

a Transmission probability (\({{{\mathcal{T}}}}\)) of various metal/MoSi2N4 and metal/WSi2N4 heterostructures. b and c show the Schottky–Mott plot for the electron SBH of MoSi2N4 and WSi2N4, respectively. d and e same as b and c, respectively, but for the hole SBH.

Full size image

Apart from tunneling probability, the extracted dTB and ΦTB can also be used to estimate the tunneling-specific resistivity (ρt)22. Based on Simmons tunneling injection model57, ρt can be obtained as,

$${\rho }_{{{\mbox{t}}}}\approx \frac{4{\pi }^{2}\hslash {d}_{{{\mbox{TB}}}\,}^{2}}{{e}^{2}}\frac{\exp \left[\frac{2{\left(2{m}_{e}\right)}^{1/2}}{\hslash }\alpha {d}_{{{\mbox{TB}}}}{{{\Phi }}}_{\,{{\mbox{TB}}}\,}^{1/2}\right]}{\frac{{\left(2{m}_{e}\right)}^{1/2}}{\hslash }\alpha {d}_{{{\mbox{TB}}}}{{{\Phi }}}_{\,{{\mbox{TB}}}\,}^{1/2}-1}$$
(5)

where α = 1 under the square-barrier approximation. For Ti and Sc contacts, ρt ≈ 0 because of the absence of the interfacial tunneling barrier. For other metal contacts, the calculated ρt lies in the typical range of 10−9 Ωcm2 which is comparable to that of the recently reported Bi/MoS2 contact of ultralow contact resistance22. The calculated ρt is listed in Supplementary Table 3 which can be readily employed for contact resistance calculation and for the analysis of device transport measurements22.

We now examine the SBHs of various metal contacts. As the semiconducting band structures of MoSi2N4 and WSi2N4, especially the CBM and VBM states, are well preserved, the electron and hole SBH can be determined from the energy differences between the CBM and the Fermi level (εF) of the metal/semiconductor heterostructure, and that between the εF and the VBM via the projected band structures and the PDOS data (see Supplementary Fig. 2). The SM plot of the metal-contacted MoSi2N4 and WSi2N4 is shown in Fig. 5b–e for both electron-type and hole-type SBH. In general, the SM plot of the electron-type SBH exhibits a positive slope with increasing metal work function. Conversely, the hole-type SBH exhibits a negative slope as dictated by the SM relation in Eq. (2). A linear fit across the 11 metal contacts reveals a remarkably large slope parameter of Se ≈ Sh = 0.69 for MoSi2N4 where Se and Sh denote electron and hole slope parameters, and Se = 0.77 and Sh = 0.76 for WSi2N4. Although being lower than that of the 2D/2D and 3D/2D VDW-type contacts17,18, these S values— achieved intrinsically without relying on VDW-type contact engineering—are still significantly higher than that of almost all previously reported 2D semiconductors14,15,27,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51 [Fig. 1e], such as MoS2 monolayer and bilayer, WS2, InSe, black and blue phosphorene, arsenene, and silicene. Such exceptionally large S values, which spans over a large metal work function range of ΔWM = 2.7 eV (i.e., WM ranging from 3.3 to 6.0 eV), indicates greater flexibility in designing metal/MoSi2N4 and metal/WSi2N4 heterostructure with a specific SBH as required by the specific device applications. For completeness, the interface potential difference ΔV is also calculated and is presented in the Supplementary Notes and Supplementary Fig. 6.

Close contacts of Pd/MoGe2P4 and Pd/WGe2P4

To further understand whether the above described built-in atomic layer protection is also present in other sister 2D semiconducting monolayers in the MA2Z4 family, such as the MoGe2P4 and WGe2P4 monolayers, we perform a close contact simulation of Pd/MoGe2P4 and Pd/WGe2P4 heterostructures. The close contact of Pd/MoGe2P4 and Pd/MoGe2P4 heterostructures are simulated by matching the 2 × 2 MoGe2P4 (WGe2P4) with the \(\sqrt{7}\times \sqrt{7}\) Pd(101) with a fixed interlayer separation of 2 Å. The lattice parameters are fixed to a/b = 3.54 Å for MoGe2P4 and a/b = 3.55 Å for WGe2P4. The lattice structures are shown in Fig. 6a, d for Pd/MoGe2P4 and Pd/WGe2P4, respectively. In the monolayer form, MoGe2P4 and WGe2P4 exhibit a band gap of 0.50 [Fig. 6b] and 0.48 eV [Fig. 6e], respectively, which are significantly smaller than those of the MoSi2N4 and WSi2N4 monolayer. Importantly, when forming contact heterostructures with Pd, although some metalization and mid-gap states are observed in the band structures and the projected electronic DOS calculations due to the stronger interaction between the metal atoms and the outermost P atoms Fig. 6c, f for Pd/MoGe2P4 and Pd/WGe2P4, respectively], it is remarkable to see that even with such a “close contact”, the semiconducting bands at the K points remain intact. The weak FLP and the protection of the semiconducting electronic bands are thus expected to present in the broader family of (Mo,W)A2Z4 with A = Si, Ge and Z = N, P. The physics of metal contacts to (Mo,W)Ge2N4 and (Mo,W)Ge2P4 shall form an interesting topic to explore in future works.

Fig. 6: Close contact simulations of Pd/MoGe2P4 and Pd/WGe2P4 with an interlayer distance of 2 Å.
figure 6

a the structure of Pd/MoGe2Si4, b electronic band structure of MoGe2P4 monolayer, c the projected electronic band structure and the partial density of states of Pd/MoGe2Si4. d–f same as a–c, respectively, for Pd/WGe2P4 contact.

Full size image

Metal contacts to bilayer MoSi2N4, MoGe2N4, and WGe2N4

We further examine three examples of metal contacts to semiconducting monolayers from the MA2Z4 family58 beyond the MoSi2N4 and WSi2N4 monolayers, namely: (i) Au/bilayer–MoSi2N459; (ii) Au/MoGe2N460; and (iii) Au/WGe2N4 contacts. The lattice structure and the electronic band structure of Au/bilayer–MoSi2N4 contact are shown in Fig. 7a, b, respectively. The MoSi2N4/Au contact exhibits a convenient Ohmic behavior with minimal metal-semiconductor hybridization. For Au/MoGe2N4 [Fig. 7c–e], an Ohmic contact is also obtained while for Au/WGe2N4 [Fig. 7f–h], the contact type exhibits an n-type Schottky contact characteristic. Importantly, the bands correspond to the semiconducting monolayers, particularly the electronic states around the VBM and CBM, remain well-intact in these contact heterostructures. These results thus suggest that the resistance against strong hybridization with the contacting metal appears to be a rather common feature among the septuple-layered semiconducting members of MA2Z4.

Fig. 7: Metal contacts to several other species of MA2Z4 monolayers.
figure 7

a, b Lattice structure, and the electronic band structure as well as the projected density of states of Au/bilayer–MoSi2N4 contact, respectively. c–e shows the lattice structure, band structure of isolated monolayer, and the band structure of the contact heterostructure with the corresponding projected density of states of Au/MoGe2N4 contact, respectively. f–h same as c–e but for Au/WGe2N4 contact.

Full size image

Discussions

Experimentally, the S values are found to be lower than the theoretically calculated S values and such deviation is often associated with the presence of defects61. For example, the presence of S vacancies in metal contacts to MoS2 has been theoretically and experimentally62,63 shown to create defect states that can pin the Fermi level and hence reduces the S value. First-principle simulations of defected metal contacts to MoSi2N4 and WSi2N4 monolayers shall quantitatively unravel how defects can affect the performance of metal contacts to these monolayers. Importantly, Sc and Ti contacts, both of which form excellent Ohmic contact with zero interfacial tunneling barrier to MoSi2N4 and WSi2N4 monolayers, are CMOS-compatible metals, thus revealing a practical contact engineering strategy for the construction of high-performance nanodevices based on MoSi2N4 and WSi2N4. For 2D metal contacts, NbS2 can be more beneficial than graphene in terms of charge injection efficiency due to the ultralow SBH59. Nonetheless, the identifications of 3D metal Ohmic contacts with zero SBH and zero interface tunneling barrier, such as Ti, clearly reveals the advantage of 3D metal contact over graphene and NbS2 towards the design of high-efficiency electrical contact to MoSi2N4 and WSi2N4 monolayers.

Recently, the edge-type contact geometry has also received much research attention both14,61 and experimentally64,65,66,67. Although the covalent-bonded heterointerface in edge-type can better facilitate charge injection, such contact geometry is faced with several challenges. The fabrication of high-quality edge-type contact remains challenging1,68, and the contact resistance of edge-type contact typically lies in the range of few tens of kΩcm264,65,66,67, which is one to two orders of magnitude higher than that of the face-type contact19,69,70,71 (see Supplementary Table 4). Recent work72 has experimentally demonstrated that the edge-type contact may not be beneficial for contact application due to the presence of pronouncing electron scatterings by defects. In addition, the edge-type contact to MoS2 is also found to be affected by a strong FLP effect (S = −0.09)61. As much interfacial physics of edge-type contact has yet to be unearthed, whether appropriately designed edge contacts to the MA2Z4 monolayers could offer a route towards high-performance contacts remains an interesting open question to be addressed in future works. Finally, we note that the contact geometry can also take a combined edge-and face-type configuration. However, due to the large surface-to-contact ratio1, the face-type contact is still expected to play a more dominant role in determining the physical properties of such combined-type contact.

In conclusion, we show that the septuple-layered morphology and the electronic properties of MoSi2N4 and WSi2N4 monolayers offer a mechanism, alternative and complementary to the VDW contact paradigm, for suppressing the FLP effect and for achieving efficient tunable SBH in metal contacts to MoSi2N4 and WSi2N4 monolayers. The origin of such efficient protection of the semiconducting electronic states and the suppression of the FLP is a combination of three unusual behaviors of MoSi2N4 and WSi2N4: (i) the septuple-layered structure which increases the atomic separation between the 2D semiconducting core layer and the external contacting metal atoms; (ii) the electronic structures in which the CBM and VBM states are concentrated in the inner core layer; and (iii) the relatively inert nature of the Si–N outermost layer. The DFT calculations presented here shall form a harbinger for the study of interfacial contact physics in the expansive family of MA2Z4. Myriads of phenomena, such as the evolution of SBH and FLP with a different number of layers73, the nature of 2D/2D and 2D/3D contacts for the other semiconducting members of the expansive MA2Z4 family, the design of MA2Z4 contact or heterostructures that can facilitate unusual non-charge transport, such as spin and valley transport74, or neuromorphic device operations13, remain to be explored. As the study of MA2Z4 monolayer and few-layer family is still in its early infancy, the experimental synthesis of this material class shall represent one of the most important research quests to be tackled before the physics and the device application potential of this material family can be better understood. Future computational and experimental studies of electrical contacts to MA2Z4 shall bring more surprises on the fundamental interface physics and chemistry, as well as the practical design of MA2Z4-based heterostructures and devices.

Methods

DFT calculations

The first-principle calculations are performed using the Vienna Ab initio Simulation Package (VASP) with projector augmented wave method75,76,77,78. The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof realization (PBE)79 is selected for the exchange-correlation functional. A kinetic energy cut-off of 500 eV is set, and the Monkhorst–Pack k mesh80 is used in the gamma-centered Brillouin zone with grids of 11 × 11 × 1 for the geometric optimizations and electronic calculations. Atomic geometry optimizations are terminated until all forces are smaller than 10−3 eV/Å to ensure accuracy. The DFT-D3 Method81 with the Grimme scheme is adopted. A vacuum space of 20 Å is set in the direction perpendicular to 3D-metal/2D-semiconductor surface. The calculations for Ni contacts are spin-polarized and the initial magnetic state for Ni substrate is set as ferromagnetic.

The 3D-metal/2D-semiconductor heterostructures are simulated by six layers of metal atoms, and two bottom layers of metals are fixed in atomic optimizations to simulate the internal atoms in the electrode. The lattice matching of the heterostructures are as followed: the 1 × 1 MoSi2N4 (WSi2N4) matches the 1 × 1 Ag(111)/Au(111)/Pd(111)/Pt(111)/Ti(0001), the \(\sqrt{3}\times \sqrt{3}\) MoSi2N4 (WSi2N4) matches the 2 × 2 Cu(111)/Ni(111)/Graphene, and the 2 × 2 MoSi2N4 (WSi2N4) matches the \(\sqrt{3}\times \sqrt{3}\) In(101)/Sc(0001)/NbS2. The contact faces of the metals are chosen based on those employed in previous DFT studies due to their low surface free energies and thermodynamical stability14,29,39. The polycrystalline face is not considered in our calculations. To avoid the properties of MoSi2N4 (WSi2N4) being affected by mechanical stress when contacted by metals, we fixed the lattice parameters of semiconductors (MoSi2N4 with a/b = 2.910 Å, and WSi2N4 with a/b = 2.913 Å) and applied strains in the metals. The lattice mismatch for all heterostructures is less than 3.8%, and the calculation details of the metal-contacted MoSi2N4/WSi2N4 monolayers are listed in Supplementary Tables 1 and 2.