Abstract
An unexploited property of graphene-based heterojunctions is the tunable doping of the junction via electrostatic gating. This unique property may be key in advancing electronic transport across interfaces with semiconductors. Here, we engineer transport in semiconducting TMDs by constructing a lateral heterostructure with epitaxial graphene and tuning its intrinsic doping to form a p–n junction between the graphene and the semiconducting TMDs. Graphene grown on SiC (epitaxial graphene) is intrinsically doped via substrate polarization without the introduction of an external dopant, thus enabling a platform for pristine heterostructures with a target band alignment. We demonstrate an electrostatically tunable graphene/MoS2 p–n junction with >20× reduction and >10× increased tunability in contact resistance (Rc) compared with metal/TMD junctions, attributed to band alignment engineering and the tunable density of states in graphene. This unique concept provides improved control over transport across 2D p–n junctions.
Similar content being viewed by others
Introduction
Engineering p–n junctions in semiconductors requires choosing the right material combination for a target band alignment. This challenge is only amplified for two-dimensional (2D) materials, specifically semiconducting transition metal dichalcogenides (TMDs) owing to their ultra-thin nature, their layered structure, and the difficulties involved with achieving sufficiently high doping densities1. While there are previous studies showing the direct synthesis and properties of lateral p–n junctions in TMD–TMD heterostructures (e.g., MoS2/WSe2, MoS2/WS2), they lack wide tunability in relative band alignments that enable minimization of interlayer resistance. Graphene grown on silicon carbide (SiC), dubbed epitaxial graphene (EG)2, provides an additional chemical degree of freedom to control the potential for only the graphene component in the heterostructure. A unique property of EG, not exploited previously in 2D heterostructures, is the ability to electrostatically modulate the intrinsic doping from n- to p-type due to the spontaneous polarization of SiC and tunability of the EG/SiC interface via intercalation3. Building from our successful synthesis of lateral heterostructures between EG and MoS24, we demonstrate the formation of a low resistance lateral p–n junction between EG and molybdenum disulfide (MoS2), which allows for configurable electronic properties. The EG is grown via silicon sublimation on SiC substrate to contact MoS2 synthesized via powder vaporization. We demonstrate that the EG/MoS2 heterostructure has a pristine interface and allows for the EG to reduce the contact resistance by >20×. This is an improvement over utilizing chemical vapor deposited (CVD) graphene, where gaseous carbon sources (e.g., methane, ethane, etc), and metal substrates (e.g., copper or nickel) are used and the graphene product is subsequently transferred onto the device substrate; the transfer process typically involves a polymer-based wet chemical etch5, which often introduces contamination into the system and deteriorates the quality of the contacts6,7,8,9. With EG contacts, the challenges involved with controllable large-area transfer is eliminated making this a scalable, as-grown process.
Results and discussion
Electrostatic doping modulation of graphene on SiC
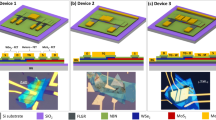
The existence of a layer of carbon atoms that are partially covalently bonded to the SiC substrate (buffer layer) between the graphene and SiC, in combination with the polarization of SiC, leads to a moderate n-type doping of as-grown EG3. The doping can be altered by intercalating hydrogen at the interface between the buffer and SiC, often accomplished by annealing the EG at elevated temperatures in a hydrogen-rich environment3. Hydrogen diffuses through defects and wrinkles in the EG, passivates dangling bonds at the buffer/SiC interface, and converts the buffer layer to an additional layer of graphene3,5. This hydrogen intercalated EG is termed quasi-freestanding EG (QFEG)5, and becomes p-type doped to compensate for the negative surface charge of the (H-passivated) Si-terminated SiC surface, so that a diverging electrostatic energy from charge-uncompensated surfaces is avoided3. Passivation of the buffer layer, and simultaneous formation of QFEG via hydrogen intercalation leads to characteristic shift of the C1s spectra in x-ray photoelectron spectroscopy (XPS), as shown in Fig. 1a5. The buffer layer initially present in the EG comprises of the S1 and S2 components, representing the sp2 and sp3 hybridized carbon in the partially covalently bonded layer. This buffer layer is removed upon hydrogenation, thus converting a monolayer of EG (+buffer) to a bi-layer QFEG system. Furthermore, in the transfer measurements of electrostatic double layer (EDL)-gated field-effect transistors (FETs), the location of the Dirac point shifts from negative for EG to positive for QFEG, further confirming the change in doping from n-type to p-type upon hydrogenation (Fig. 1b). Here, the term Dirac point is used to locate the voltage at which the current reaches its minimum in the ambipolar graphene, thus applicable for both monolayer EG and bi-layer QFEG. Electronic band alignments of n-type EG and p-type QFEG with conventional metals (e.g., titanium, gold), and commonly studied TMDs10 are shown schematically in Fig. 1c2.
a C1s spectra in x-ray photoelectron spectroscopy (XPS) splits upon hydrogenation, is indicative of intercalated graphene devoid of the buffer layer. b Transfer curves of monolayer epitaxial graphene (EG) and bi-layer quasi-freestanding epitaxial graphene (QFEG) shows the change in the position of the Dirac point before and after hydrogenation indicating the n-type doping and the p-type doping, respectively. c Band alignments of several semiconducting TMDs with conventional contact metals like titanium and gold, and n-type EG and p-type QFEG. These numbers have been extracted from literature and experimental values (adapted from ref. 10).
Device characteristics of EG/MoS2 and QFEG/MoS2 lateral heterostructures
Direct synthesis of MoS2/EG lateral heterostructures enables configurable transport properties of MoS2 because the carrier type of EG is predetermined by hydrogen intercalation, and the heterostructure system is reconfigurable via EDL gating. We employ p-type QFEG to synthesize p–n junctions with n-type MoS2. The advantage of using this system is twofold: (1) this system exhibits a significant reduction in contact resistance, when compared with conventional metals, and (2) unlike the EG/MoS2 system, the QFEG/MoS2 is a p–n junction, which leads to greater tunability via EDL gating. In fact, the contact resistances of QFEG/MoS2 can change by >10× upon application of gate voltage Vg (Fig. 2a). Thus, the controlled doping modulation of EG allows for the formation of these unique graphene/MoS2 heterostructure p–n junctions, which have lower contact resistances than conventional metals.
a Contact resistance (Rc, kΩ·µm) versus Gate Voltage (Vg, V) - values extracted using transfer length measurements. Both QFEG/MoS2 and EG/MoS2 heterostructures show similar values of contact resistance at gate voltages (Vg) of +3V. The modulation in the values of Rc for the QFEG/MoS2 junction allows it to be a truly tunable p-n junction. Inset: Side-gated transistor structure constructed for electrostatic double layer gating using (PEO)76:CsClO4. b Sheet resistance (Rs, kΩ/◽) also shows the same characteristic trend for both the QFEG/MoS2 and the EG/MoS2 heterostructures.
To evaluate the tunability, three types of structures are constructed and characterized: QFEG/MoS2 (Fig. 2 and Supplementary Fig. 2), EG/MoS2 (Fig. 2 and Supplementary Fig. 2), and metal/MoS2 (Supplementary Fig. 2). EG (and QFEG) is grown (and hydrogenated) on SiC substrates and patterned into rectangular contact pads using optical lithography. Subsequently, MoS2 is grown using powder vaporization of molybdenum tri-oxide (MoO3) and sulfur (S), as described in ref. 4. Such lateral heterostructures exhibit a pristine interface with an overlap of MoS2 onto the edge of the graphene pattern (see Supplementary Note 1)4. Achieving a clean interface enables efficient electronic coupling between EG (or QFEG) and MoS2, leading to an effective graphene contact to MoS2. We note that the MoS2 grown via powder vaporization (PV) is n-type doped due to the combined effects of a low vacuum-level-referenced band edge positions11 (relative to other TMDs) and the presence of defects and typical non-uniformity based on the PV method12.
The p–n junction barrier, and consequently the resistance at the junction (contact resistance (Rc)), is evaluated via conventional transfer length measurements, also known as transmission line measurements (TLM). EDL-gated transistors are fabricated post growth using a side gate geometry (inset, Fig. 2a). QFEG and EG exhibit comparable contact resistance values at a gate voltage (Vg) of +3 V, and >20× reduction in Rc compared with conventional titanium/gold (Ti/Au) metal stacks (see Supplementary Note 2). This tunability can be attributed to the low density of states in graphene13,14 compared with metal. The constructed lateral heterostructure that allows the EDL gating of the EG as well as MoS2, providing a means of electrostatic modulation of the metal/EG/MoS2 band alignment and a gate-dependent contact resistance. Thus, EG and QFEG are considered an electrostatically tunable contacts. Such tunable contacts are key in various chemical and optical sensors15,16,17,18. The ability to tune the Fermi levels using Vg and locking the system at a predetermined electronic configuration is of great interest in the sensor community. Graphene offers a unique contact to other 2D materials such as MoS2 because the Fermi level of graphene can be readily modulated, along with the semiconducting MoS2, providing an additional mode of tunability absent in metal contacts. Electrostatically tunable EG provides an additional “knob” with its unique property of enabling electrostatic modulation of the intrinsic doping from n- to p-type3.
The QFEG/MoS2 interface resistance can be modulated by >10× as a function of Vg (−3 to +3 V), providing evidence of a highly tunable p–n junction. The large modulation of QFEG/MoS2 is correlated with a larger electronic barrier as compared with the case of EG, thus making it sensitive to an external electric field and enabling efficient charge separation. The sheet resistance (Rs) (Fig. 2b) exhibits a similar trend as Rc, also representative of the barrier at the QFEG/MoS2 p–n junction. Although, the Rc and Rs values are lower for the EG/MoS2 case, the absence of a p–n junction does not allow this lateral EG/MoS2 heterostructure to be employed in many cases aside from unipolar FETs (see Supplementary Note 3). For functionality that requires a p–n junction and charge separation, the QFEG/MoS2 system is a unique solution that takes advantage of the high conductivity of graphene that allows for improved electronic and thermal transport in the system, which would not be possible in a TMD/TMD p–n junction.
Visualization and calculations of band alignments
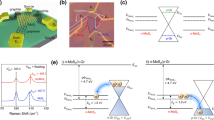
Electronic band structure alignments are key to understanding the heterojunctions formed at interfaces of 2D materials. To further our understanding of the tunability of the p–n QFEG/MoS2 lateral heterostructure system, we investigate the relative electronic band alignments experimentally and verify it using density functional theory (DFT). Angle-resolved photo-emission spectroscopy (ARPES) is used to directly visualize the band alignments, and contrast QFEG/MoS2 and EG/MoS2 junctions. As shown in Fig. 3a, b, the graphene19 as well as the averaged MoS2 valence bands are compared, including the MoS2 at the interface and away from it20. ARPES across the QFEG/MoS2 interface in Fig. 3a reveals two valence bands filled below the charge neutrality point typical of p-type bi-layer graphene, whereas the MoS2 valence band now extends up to approximately −1 eV binding energy at Γ. In contrast, for ARPES across the EG/MoS2 interface shown in Fig. 3b, we observe a complete Dirac cone filled above the Dirac point at the K-point, indicative of n-type monolayer graphene, while the intense valence band signature of MoS2 appears at approximately −1.3 eV at Γ. The band bending diagrams in Fig. 3c, d quantify the band alignment for the QFEG and EG cases, respectively, where the MoS2 levels can be deduced from the respective work functions of QFEG and EG, reported to be \(\phi _{QFEG} = - 4.7\) eV and \(\phi _{EG} = - 4.2\) eV (see Supplementary Note 4 for comparisons with theoretical values from literature). We focus on quantifying the valence band maximum (VBM) level relative to vacuum (i.e., before contact) rather than the Fermi level in MoS2 since the former is intrinsic to the material. For EG, µ-ARPES reveals a spread in the VBM from −1.5 to −2.2 eV, as indicated by the two green arrows and consistent with direct measurements of band bending from nano-ARPES data (published elsewhere) where an upwards bending of MoS2 bands toward the MoS2/graphene interface was found. Thus, the MoS2 VBM relative to the vacuum level can be estimated to be \(-4.2-1.5 = -5.7\) eV. Similarly, for QFEG, we estimate the band bending from the VBM spread in µ-ARPES from −1.0 to −1.8 eV, yielding an estimated MoS2 VBM of −5.7 eV. Although, estimating VBM positions from the magnitude of band spreading in µ-ARPES is less direct than nano-ARPES (since the band bending may not reach asymptote values limited by the laser spot size), the fact that the EG and QFEG cases gave identical values suggest reasonable accuracy. The measured VBM is compared with the vacuum-level-referenced VBM calculated for monolayer, bi-layer, and bulk MoS2 as shown in Fig. 3e from many-body perturbation theory within the GW approximation to the electronic self energy21,22,23,24. Considering that further accounting for the dielectric screening from the substrate25 and carriers26 would yield a VBM higher by ~0.2 eV, the quasiparticle ionization potential of the bilayer case at −5.9 eV appears to be the best match. This is also corroborated with a cross-sectional transmission electron micrograph in Supplementary Note 5 showing a bilayer MoS2 in the channel.
a, b Angle-resolved photoemission spectroscopy with a µm resolution (µ-ARPES) for the QFEG/MoS2 and the EG/MoS2 lateral heterostructure system respectively. The K-point of graphene and the Γ-point of MoS2 is observed together upto the filled Fermi energy level (EF). c, d Schematic band diagrams for corresponding µ-ARPES measurements in (a) and (b) respectively using values of valence band maximum (VBM) calculated from density functional theory (DFT). The three band structures in panels (c, d) represent bands from MoS2 far and near the junction and graphene bands, from left to right. e Band edge positions for monolayer (left), bi-layer (middle), and bulk MoS2 (right) calculated at the DFT-PBE level (blue) and GW level (red). The VBM estimated from ARPES is marked by the green horizontal line at –5.7 eV.
Outlook
In summary, we have established a facile route to tune the transport properties of MoS2-based devices by introducing tunable graphene in the system leading to the synthesis of tunable p–n junctions. This allows for improved electronic conduction compared with conventional p–n junctions with two semiconducting components. This study exploits the property of tuning the doping of EG via hydrogen intercalation to form p-type doped QFEG and using it as one of the components of the p–n junction. We have also compared the QFEG/MoS2 p–n junction with the previously synthesized EG/MoS2 n+–n junction and studied the electronic band alignments via ARPES and corroborated it using theoretical calculations. Along with this in-depth knowledge of band alignments in as-grown heterostructures and the band alignment diagram shown in Fig. 1c, this study enables application-specific growth of heterostructures with target band alignments and study of interfaces.
Methods
Synthesis of EG and QFEG
EG is grown in a three-phase, hot-zone, graphite furnace (Thermal Technology LLC) via silicon sublimation from the 6H SiC(0001) face. The SiC is first cleaned using organic solvents and then annealed in 10% hydrogen (balance argon) at 1500 °C for 30 min to eliminate subsurface damage due to chemical and mechanical polishing. The H2 is then removed from the system, and the temperature is increased to 1800 °C for 10 min at 500 Torr to form the graphene layers. This process yields low defect density multi-layer EG. Upon annealing the EG in 100% H2 at 900 °C for 30 min at a pressure of 600 Torr, the hydrogen intercalates and converts the n-type EG to a p-type QFEG4.
Synthesis of MoS2
Powder vaporization in a horizontal quartz tube furnace is used to synthesize MoS2, using 2–3 mg of MoO3 powder and 200 mg S as the precursors. The system is purged with argon to atmospheric pressure (~710 Torr), and S is independently heated to 130 °C to provide a continuous S flow during the MoS2 growth, which occurs at 800 °C for 15 min4.
Device fabrication
Prior to MoS2 growth, both EG and QFEG are patterned using standard ultraviolet photolithography. A TLM pattern of graphene contacts with a variable channel spacing (ranging from 0.75 to 10 µm) is produced using a photoresist double stack (PMGI SF2 + SPR 3012) exposed using a Stepper 8500. A mixture of oxygen and argon (O2/Ar) is used for a reactive ion etch to remove the EG outside of the patterns, leaving behind a series of periodically spaced graphene rectangles of fixed length (5 µm), which ultimately constitute the contacts to the MoS2 channel for transistor fabrication. After the synthesis of the MoS2/EG or MoS2/QFEG heterostructure, an (SF6)/O2 reactive ion etch is used to remove the excess MoS2, thereby isolating any MoS2 growth strictly between the graphene electrodes. Subsequently, contact regions are lithographically patterned, briefly exposed to an O2 plasma, and Ti/Au (5/15 nm) metal is deposited via electron-beam evaporation, followed by lift off in PRS 3000 photoresist remover4.
Electrolyte deposition and I–V measurements
The polymer electrolyte preparation details are the same as published by Xu et al., where the electrolyte is prepared and deposited in an argon-filled glove box with concentrations of H2O and O2 < 0.1 parts-per-million (ppm)27. The solid polymer electrolyte (PEO)76:CsClO4 is deposited on the device by drop-casting onto ∼1 × 1 cm2 substrates in an argon ambient and annealed on a hotplate at 80 °C. The sample is then transferred from the glove box to the probe station through an Ar-filled load lock. The entire process of electrolyte preparation, deposition, transfer to the probe station, and measurement is completed under an inert gas environment with no sample exposure to ambient. Electrical measurements are performed on a Lake Shore cryogenic vacuum probe station (CRX-VF) under ∼10−6 Torr at 300 K using a Keysight B1500A semiconductor parameter analyzer. For transfer curves, the voltage sweep rate is optimized at ∼0.67 mV/s to minimize hysteresis. Four TLM sets (0.75–10 µm) were measured both for the heterostructures and the MoS2-only devices to extract contact resistance and sheet resistance. For transfer curves, five devices were measured for each channel length, and several such devices with different channel lengths were measured. Supplementary Note 2 shows the repeatability of the data and its variation with different voltage sweep rates and hysteresis.
ARPES measurements
ARPES experiments were performed at the μ-ARPES end-station of the Microscopic and Electronic Structure Observatory at the Advanced Light Source in Berkeley, USA. As-grown samples were introduced into ultra-high vacuum (<5 × 10−11 mbar) and outgassed at 100 °C. Data were collected at 80 K temperature with p-polarized light of hν = 145 eV photon energy, employing a hemispherical Scienta R4000 electron analyzer equipped with custom made deflectors19,20. These enable the collection of ARPES spectra over an entire Brillouin Zone without moving the sample and thus allow to retain the X-ray focus on the small sample structures without drift. The synchrotron beam-spot size was on the order of 20 μm, on the order of the feature size of the graphene/MoS2 structure. ARPES thus integrates over band bending effects across the interface, which explains the valence band smearing in the data of Fig. 3d.
Theory calculation
For the GW calculations for monolayer (bilayer) MoS2, we employ a 18 × 18 × 1 k-point grid, a truncated Coulomb interaction28, a planewave energy cutoff of 15 Ha, and 250 (500) empty bands for the evaluation of the dielectric matrix within the random-phase approximation. The Godby–Needs-generalized plasmon-pole model29 was used to extend the static dielectric matrix to finite frequencies. Correction to the dielectric matrix and the self energy were applied with and extrapolar energy of 2.7 Ha to accelerate the convergence of absolute band levels with respect to the empty bands included in the summation30. Quasiparticle shifts (relative to DFT levels) are then superimposed on DFT levels referenced from the vacuum level to obtain the final level alignments. All calculations are performed using the ABINIT code31.
Data availability
The data that support the findings of this study are available from the authors on reasonable request, see author contributions for specific data sets.
References
Briggs, N. et al. A roadmap for electronic grade 2D materials. 2D Mater. 6, 022001 (2019).
Riedl, C., Coletti, C. & Starke, U. Structural and electronic properties of epitaxial graphene on SiC(0 0 0 1): a review of growth, characterization, transfer doping and hydrogen intercalation. J. Phys. D. Appl. Phys. 43, 374009 (2010).
Ristein, J., Mammadov, S. & Seyller, T. Origin of doping in quasi-free-standing graphene on silicon carbide. Phys. Rev. Lett. 108, 246104 (2012).
Subramanian, S. et al. Properties of synthetic epitaxial graphene/molybdenum disulfide lateral heterostructures. Carbon 125, 551–556 (2017).
Riedl, C., Coletti, C., Iwasaki, T., Zakharov, A. A. & Starke, U. Quasi-free-standing epitaxial graphene on SiC obtained by hydrogen intercalation. Phys. Rev. Lett. 103, 246804 (2009).
Liu, K.-K. et al. Growth of large-area and highly crystalline MoS2 thin layers on insulating substrates. Nano Lett. 12, 1538–1544 (2012).
Pu, J. et al. Highly flexible MoS2 thin-film transistors with ion gel dielectrics. Nano Lett. 12, 4013–4017 (2012).
van der Zande, A. M. et al. Grains and grain boundaries in highly crystalline monolayer molybdenum disulphide. Nat. Mater. 12, 554–561 (2013).
Robinson, J. A. et al. Contacting graphene. Appl. Phys. Lett. 98, 053103 (2011).
Schulman, D. S., Arnold, A. J. & Das, S. Contact engineering for 2D materials and devices. Chem. Soc. Rev. 47, 3037–3058 (2018).
Liu, Y., Stradins, P. & Wei, S. H. Van der Waals metal-semiconductor junction: weak Fermi level pinning enables effective tuning of Schottky barrier. Sci. Adv. 2, 1–7 (2016).
Zhang, K. et al. Manganese doping of monolayer MoS2: the substrate is critical. Nano Lett. 15, 6586–6591 (2015).
Dröscher, S. et al. Quantum capacitance and density of states of graphene. Appl. Phys. Lett. 96, 152104 (2010).
Novoselov, K. S. et al. Electronic properties of graphene. Phys. Status Solidi 244, 4106–4111 (2007).
Fan, Z. & Lu, J. G. Gate-refreshable nanowire chemical sensors. Appl. Phys. Lett. 86, 123510–123510-3 (2005).
Tsai, M.-Y. et al. Flexible MoS2 field-effect transistors for gate-tunable piezoresistive strain sensors. ACS Appl. Mater. Interfaces 7, 12850–12855 (2015).
Xu, H. et al. High responsivity and gate tunable graphene-MoS2 hybrid phototransistor. Small 10, 2300–2306 (2014).
Vélez, S. et al. Gate-tunable diode and photovoltaic effect in an organic–2D layered material p–n junction. Nanoscale 7, 15442–15449 (2015).
Bostwick, A., Ohta, T., Seyller, T., Horn, K. & Rotenberg, E. Quasiparticle dynamics in graphene. Nat. Phys. 3, 36–40 (2007).
Katoch, J. et al. Giant spin-splitting and gap renormalization driven by trions in single-layer WS2/h-BN heterostructures. Nat. Phys. 14, 355–359 (2018).
Jin, C., Rasmussen, F. A. & Thygesen, K. S. Tuning the Schottky barrier at the graphene/MoS2 interface by electron doping: density functional theory and many-body calculations. J. Phys. Chem. C. 119, 19928–19933 (2015).
Liang, Y., Huang, S., Soklaski, R. & Yang, L. Quasiparticle band-edge energy and band offsets of monolayer of molybdenum and tungsten chalcogenides. Appl. Phys. Lett. 103, 042106 (2013).
Komsa, H. P. & Krasheninnikov, A. V. Native defects in bulk and monolayer MoS2 from first principles. Phys. Rev. B - Condens. Matter Mater. Phys. 91, 1–17 (2015).
Schlaf, R., Lang, O., Pettenkofer, C. & Jaegermann, W. Band lineup of layered semiconductor heterointerfaces prepared by van der Waals epitaxy: charge transfer correction term for the electron affinity rule. J. Appl. Phys. 85, 2732–2753 (1999).
Naik, M. H. & Jain, M. Substrate screening effects on the quasiparticle band gap and defect charge transition levels in MoS2. Phys. Rev. Mater. 2, 1–8 (2018).
Gao, S. & Yang, L. Renormalization of the quasiparticle band gap in doped two-dimensional materials from many-body calculations. Phys. Rev. B 96, 1–8 (2017).
Xu, K. et al. Pulse dynamics of electric double layer formation on all-solid-state graphene field-effect transistors. ACS Appl. Mater. Interfaces 10, 43166–43176 (2018).
Ismail-Beigi, S. Truncation of periodic image interactions for confined systems. Phys. Rev. B Condens. Matter Mater. Phys. 73, 1–4 (2006).
Godby, R. W. & Needs, R. J. Metal-insulator transition in Kohn-Sham theory and quasiparticle theory. Phys. Rev. Lett. 62, 1169–1172 (1989).
Bruneval, F. & Gonze, X. Accurate GW self-energies in a plane-wave basis using only a few empty states: Towards large systems. Phys. Rev. B - Condens. Matter Mater. Phys. 78, 1–9 (2008).
Gonze, X. et al. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 180, 2582–2615 (2009).
Acknowledgements
S.S. and J.A.R. acknowledge funding from NSF CAREER (Award: 1453924). Y.W. and V.H.C. acknowledge support from the 2D Crystal Consortium National Science Foundation (NSF) Materials Innovation Platform under cooperative agreement DMR-1539916. J.A.R. and N.A.S. acknowledge the Center for Atomically Thin Multifunctional Coatings (ATOMIC), sponsored by the National Science Foundation (NSF) division of Industrial, Innovation & Partnership (IIP) (Award: 1540018). D.D., J.A.R., S.K.F.-S., and K.X. acknowledge the funds by the Center for Low Energy Systems Technology (LEAST), one of the six centers of STARnet, a Semiconductor Research Corporation program sponsored by MARCO and DARPA. S.K.F.-S. and K.X. acknowledge funding from NSF-DMR-EPM (Award: 1607935). S.M. acknowledges support by the Swiss National Science Foundation (Grant No. P300P2-171221). This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under Contract No. DE-AC02-05CH11231. S.S. and J.A.R. also thank Prof. Randall M. Feenstra from Department of Physics, Carnegie Mellon University, Pittsburgh and his graduate students, Jun Li and Dacen Waters for their help and guidance with data related to this project. The authors would also like to acknowledge the staff members at the nanofabrication facility at Materials Research Institute and the Materials Characterization Laboratory at The Pennsylvania State University, whose help and guidance was key to accomplishing the goals of the project.
Author information
Authors and Affiliations
Contributions
S.S., K.X., S.K.F.-S., and J.A.R. wrote the paper with input from co-authors. S.S. performed the synthesis of EG and QFEG, the lateral heterostructures and constructed the devices using the nanofabrication facility in Materials Research Institute at The Pennsylvania State University. S.S. characterized the lateral heterostructures using XPS and Raman spectroscopy. K.X. and S.S. performed the EDL-gated measurements on the FETs at the Fullerton lab at University of Pittsburgh. K.X., S.S., and S.K.F.-S. discussed extensively to extract conclusions from the electrical data. Y.W. performed the DFT calculations for the VBM measurements under the guidance of V.H.C.Y.W. and S.S. collated the data from VBM measurements and the µ-ARPES. S.M. performed the µ-ARPES measurements at the Advanced Light Source. N.A.S. performed the synthesis of the lateral heterostructures using powder vaporization along with S.S.D.D. and S.S. designed the process flow for device fabrication in the nanofabrication facility. D.D. and S.S. also worked closely to characterize the synthesized heterostructures via scanning electron microscopy.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Subramanian, S., Xu, K., Wang, Y. et al. Tuning transport across MoS2/graphene interfaces via as-grown lateral heterostructures. npj 2D Mater Appl 4, 9 (2020). https://doi.org/10.1038/s41699-020-0144-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-020-0144-0
This article is cited by
-
Charge state-dependent symmetry breaking of atomic defects in transition metal dichalcogenides
Nature Communications (2024)
-
Optoelectronic Properties of MoS2/Graphene Heterostructures Prepared by Dry Transfer for Light-Induced Energy Applications
Journal of Electronic Materials (2022)
-
Electron–phonon coupling in superconducting 1T-PdTe2
npj 2D Materials and Applications (2021)
-
Spin-dependent vibronic response of a carbon radical ion in two-dimensional WS2
Nature Communications (2021)