Abstract
Inter-layer excitons (IXs) in hetero-bilayers of transition metal dichalcogenides (TMDs) represent an exciting emergent class of long-lived dipolar composite bosons in an atomically thin, near-ideal two-dimensional (2D) system. The long-range interactions that arise from the spatial separation of electrons and holes can give rise to novel quantum, as well as classical multi-particle correlation effects. Indeed, first indications of exciton condensation have been reported recently. In order to acquire a detailed understanding of the possible many-body effects, the fundamental interactions between individual IXs have to be studied. Here, we trap a tunable number of dipolar IXs (NIX ~ 1–5) within a nanoscale confinement potential induced by placing a MoSe2–WSe2 hetero-bilayer (HBL) onto an array of SiO2 nanopillars. We control the mean occupation of the IX trap via the optical excitation level and observe discrete sharp-line emission from different configurations of interacting IXs. The intensities of these features exhibit characteristic near linear, quadratic, cubic, quartic and quintic power dependencies, which allows us to identify them as different multiparticle configurations with NIX ~ 1–5. We directly measure the hierarchy of dipolar and exchange interactions as NIX increases. The interlayer biexciton (NIX = 2) is found to be an emission doublet that is blue-shifted from the single exciton by ΔE = (8.4 ± 0.6) meV and split by 2J = (1.2 ± 0.5) meV. The blueshift is even more pronounced for triexcitons ((12.4 ± 0.4) meV), quadexcitons ((15.5 ± 0.6) meV) and quintexcitons ((18.2 ± 0.8) meV). These values are shown to be mutually consistent with numerical modelling of dipolar excitons confined to a harmonic trapping potential having a confinement lengthscale in the range \(\ell \approx 3\) nm. Our results contribute to the understanding of interactions between IXs in TMD hetero-bilayers at the discrete limit of only a few excitations and represent a key step towards exploring quantum correlations between IXs in TMD hetero-bilayers.
Similar content being viewed by others
Introduction
HBLs of van-der-Waals bonded 2D TMDs1,2,3,4,5,6,7,8,9 feature an atomically sharp interface with a type-II band alignment and frontier orbital couplings defined by the mutual angular orientation of the basal plane of the component layers1. Such atomically thin 2D heterointerfaces can host IXs—Coulomb-bound states of electrons (e) and holes (h) located in the different component monolayers1. The spatial separation of e and h gives rise to a significantly increased lifetime compared to intralayer excitons1,3,10 and a static electric out-of-plane dipole moment with a magnitude |pz|/e ~ 0.7 nm for the MoSe2–WSe2 heterointerface1. The enhanced radiative lifetime of IXs allows them to cool towards the lattice temperature before recombination takes place, whereas the large static dipole moment facilitates tuning of the IX energy1,11,12 and lifetime11,12 using static electric fields. In optical experiments, dipole–dipole repulsion between IXs gives rise to strongly blueshifting emission with increasing IX density and the potential to explore the many-body physics of dipolar composite bosons in a solid-state system1,3,10. It has also been demonstrated that applying strain to the HBL can strongly tune the IX energy13; a method that is routinely used to define exciton trapping potentials in monolayer TMDs14,15,16. Overall, IXs constitute a highly tunable platform for optically exploring and controlling interacting gases of dipolar excitons in the solid state.
Results and discussion
Trapping interlayer excitons
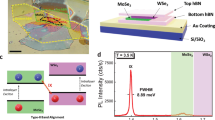
Our sample structure is schematically depicted in Fig. 1a. It consists of stacked monolayers of WSe2 and MoSe2 that form a HBL, which is then transferred onto a SiO2 substrate patterned with nanopillars having a height of ~90 nm and diameter ~130 nm (see “Methods”). Figure 1b (enhanced in Supplementary Note 1) shows an optical micrograph of the sample in which the monolayer MoSe2, WSe2 and HBL regions can be seen, as well as the nanopillars in the HBL region. The contours of the WSe2 and MoSe2 monolayers are outlined with blue and orange dashed lines, respectively, and pillars that did not pierce the TMD layers appear as black dots. Figure 1c shows normalized spectra recorded from three different unstrained sample regions, namely the WSe2 monolayer, the MoSe2 monolayer and the WSe2–MoSe2-HBL away from the nanopillars. These spectra were recorded at T = 10 K with cw excitation at 633 nm and a power of Pex = 35 μW focused to ~1 μm. Both, WSe2 and MoSe2, have prominent emission features at their characteristic exciton and trion energies at 1.75 eV and 1.72 eV17, and 1.66 eV and 1.63 eV18, respectively. Furthermore, the WSe2 component monolayer exhibits a broader band of unresolved emission at lower energies (1.60–1.70 eV) that has been identified as stemming from dark excitons19,20 and trions21, charged biexcitons22,23,24,25,26 and defect-bound excitons27,28. Each of these emission features are also present in the HBL region, albeit strongly quenched, due to interlayer charge transfer that occurs over sub-picosecond timescales, faster than the exciton lifetime29,30,31. The most prominent emission feature from the HBL is at ~1.38 eV and is attributed to IXs formed by an electron in the MoSe2 and a hole in the WSe21. This attribution is supported by the emission energy and the characteristically asymmetric lineshape featuring red-shifted emission from momentum-indirect IXs10. Figure 1e shows the power dependence of the IX emission revealing a significant blueshift (≥20 meV) arising from repulsive dipolar interactions in the gas of IX for increasing excitation levels3,32. We note that this blueshift does not occur over the whole range of excitation levels, but rather exhibits an onset close to Pex ~ 30 nW, marking a low-density regime where dipolar interactions are weak (see Supplementary Note 2). Furthermore, the low-density IX regime also manifests itself by a deviation from the \(\sqrt {P_{ex}}\) dependence of the IX emission intensity, which might be indicative of non-radiative exciton–exciton annihilation33 only above a threshold density.
a Schematic represenation, and b optical micrograph of the sample used in this work. The monolayers of WSe2 and MoSe2 are outlined with blue and orange dashed lines, respectively. The nanopillars appear as black dots in the heterobilayer region. c Example spectra recorded from the unstrained monolayer and heterobilayer regions. d Typical μPL spectra recorded from three pillar sites (A, B and C as marked in a) in the heterobilayer region and a reference spectrum from the unstrained heterobilayer. Inset: example spatially resolved integrated PL intensity of a low-energy emission peak at pillar A. e, f Intensity-normalized PL spectra recorded from the HBL at different excitation powers at a position outside the pillar region (e) and on pillar A (f). All spectra were recorded at 10 K and, besides the power-dependent measurements shown in panels e and f, subject to strong continuous wave (cw) excitation at 633 nm using a power of 35 μW focused to a spot-size of ~1 μm.
The nanopillars have a strong impact on the IX emission spectra. Typical data is presented in Fig. 1d that compares emission of unstrained regions of the HBL with that recorded from three pillar sites (labelled A, B and C as in Fig. 1a). The characteristic IX emission at 1.38 eV can still be observed in each emission spectrum since the probed sample volume is much larger than the nanopillar size. However, additional peaks emerge in the vicinity of the nanopillar sites, red-shifted by up to ~100 meV from the peak of the free IX emission. The observation of a pronounced red-shift is similar to reports of strain-induced bandgap modulation in monolayer MoSe216, MoS234 and particularly WSe214,15, where this effect is routinely used to generate quantum emitters. We attribute these features to localized interlayer excitons (LIXs) at the pillar sites, most likely due to strain-related trapping potentials around the nanopillar. The interlayer exciton character is confirmed by PL-excitation spectroscopy detected on the LIX features, that clearly reveals free exciton fingerprints of both MoSe2 and WSe2 component monolayers, and time-resolved PL measurements, that show similar radiative decay times for localized and free IXs (see Supplementary Notes 3 and 4). To illustrate the confinement of the LIX features to the pillar sites, the inset of Fig. 1d shows the spatially resolved emission intensity of an example LIX peak at pillar site A. The spatial extent of this feature is clearly limited by the spatial resolution of our μPL setup (1 µm), indicative of a point-like source. Figure 1e, f compare normalized IX μPL spectra plotted as a function of excitation power from the flat region of the HBL and on pillar A, respectively. In both cases, free IX emission is observed that blueshifts by up to ~20 meV over the examined power range. The spectra recorded from pillar A additionally exhibit discrete LIX emission lines. Individually, these features do not blueshift with excitation power, in strong contrast to the broad IX peak. Instead, changes of excitation power result in a redistribution of the PL intensity among the different LIX peaks. However, if one analyses the entirety of all LIX emission peaks and determines its center of the spectral weight as a function of excitation power (see Supplementary Note 5), one finds a collective LIX blueshift which is slightly stronger than that of the free IX, consistent with stronger interactions for IXs spatially confined to a trapping potential. This effect of the LIX emission shifting among several discrete peaks with varying excitation power was observed for all pillars exhibiting LIX emission (see Supplementary Note 6) and was reproducible following thermal cycling. Exemplary polarization-resolved LIX spectra are shown in Supplementary Note 7.
Spectroscopy of trapped few-exciton states
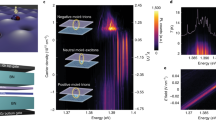
The LIX emission spectra of pillar A for excitation powers ranging from 79 nW to ≥500 nW, two orders of magnitude weaker than the power used to record the results depicted in Fig. 1, are presented in Fig. 2a (see Supplementary Note 8 for additional spectra). At the lowest excitation power, the emission spectrum is found to be dominated by a single sharp line at 1.302 eV, labelled LIX1 in the figure. The spectral linewidth of this peak is 550 μeV and it is broadened on the low-energy flank, most likely due to coupling to acoustic phonons35. The integrated intensity of LIX1 is plotted in Fig. 2b as a function of the excitation power. From the lowest excitation levels investigated, it increases linearly with power, as can be seen from the solid line on the figure that shows a fit to the data with I = I0 × Pα yielding α = 0.9 ± 0.1. The dotted line on the figure shows our expectations for a linear power dependence. This observation, combined with the saturation and eventual decrease of the peak intensity at the highest excitation levels investigated, clearly identifies this peak as stemming from the recombination of a single IX in the local trapping potential, as is commonly observed in the emission characteristics of III–V quantum dots and other discrete quantum emitters36. As the excitation power is increased from the minimum of 79 nW, additional emission features emerge at higher energies, the most prominent of which is a pair of lines labelled LIX2A and LIX2B in Fig. 2. In contrast to LIX1, LIX2A/B both exhibit a near quadratic power dependence (α2A = 1.96 ± 0.15, α2B = 1.57 ± 0.12) and each saturates and quenches at the highest pump powers investigated (see Fig. 2b). For excitation power in excess of ~300 nW, additional manifolds of emission lines emerge, labelled LIX3A/B, LIX4 and LIX5 on Fig. 2a. The power dependence of each emergent set of lines clearly becomes successively more superlinear in behaviour—LIX3A/B have a power dependence that is very close to cubic (α3A = 3.48 ± 0.27, α3B = 3.6 ± 0.7), LIX4 close to quartic (see dotted lines on figure). These observations mirror previous findings for multi-exciton states in semiconductor quantum dots36,37 and double quantum wells38. Since there were only a few data points before saturation for some of the peaks, we substantiate our particle number assignment by comparing ratios of intensities of two peaks to an independent capture model (see Supplementary Note 9). This method uses data from the entire available power range.
a PL spectra of localized IXs at the same pillar for varying powers. b Intensity of individual emission peaks determined by integrating the signal in a narrow spectral region around the peak center plotted as a function of excitation power. The characteristic power exponents of the intensity dependencies are given in the main text. The grey dashed line denotes the onset of saturation effects. c Emission energies of the different LXIi peaks presented in panel a plotted as a function of excitation power. Error bars represent fit uncertainties.
Figure 2c shows the emission energies of the various LIX peaks as extracted from multiple peak fitting. The energy of the individual LIXi peaks is not significantly power dependent, beyond spectral wandering. This can be prominently seen in the LIX1 peak, which jitters by up to ~1 meV between measurements. Similar spectral wandering has also been reported from discrete emitters in monolayer WSe2, where it is commonly attributed to time-dependent fluctuations in the local electrostatic environment39,40. The mid-point of the biexciton LIX2 doublet is significantly blueshifted by (8.4 ± 0.6) meV with respect to LIX1 and the two components are separated by ~(1.2 ± 0.5) meV.
Modelling interactions in multi-exciton complexes
In order to quantitatively understand the strong blueshift of the localized interlayer biexciton from the single exciton and the splitting of the biexciton into a doublet, we modelled the interaction of two IXs confined to a harmonic trapping potential, as characterised by a confinement lengthscale \(\ell = \sqrt {\hbar /m^ \ast {\mathrm{\Omega }}_0}\). Here, m* denotes the total effective mass of the exciton (sum of electron and hole mass) and Ω0 is the angular frequency of an exciton in the harmonic potential. Figure 3a illustrates how we calculate the equilibrium separation Δρ between two IXs by minimizing the sum of repulsive (dipolar) and attractive (harmonic) potential energies. For values of \(\ell\) ~ 3–4 nm, reference to Fig. 3a shows that Δρ ~ 4.5–5.5 nm. We now continue to discuss the calculation of the direct and exchange Coulomb interaction energies for the LIX2 and LIX1 states. For this purpose, we modified the method outlined in ref. 41 (see Supplementary Note 10) and start with a Hamiltonian describing the biexciton complex of the following form:
where
describes non-interacting excitons exposed to a weak harmonic confinement potential and
represents the Coulomb interactions between the excitons. In Eqs. 2 and 3, the coordinates ρ1 and ρ2 are in-plane projections of the relative electron-hole coordinates of the interlayer excitons, as depicted in Fig. 3b, and Δρ was introduced before. Moreover, d ≈ 0.7 nm is the interlayer separation of the HBL that determines the strength of the dipole–dipole repulsion and ε = ε0εr describes the effective dielectric screening by the surrounding vacuum (upper) and SiO2 (lower) media. We note that, in the simplest picture in which we average the values for vacuum (upper cladding) and SiO2 (lower substrate), the effective dielectric constant would be \(\epsilon _r = \left( {\epsilon _{{\mathrm{vac}}} + \epsilon _{{\mathrm{SiO}_{2}}}} \right)/2\sim 2.5\). For the effective masses m*, we use m* = 0.8m0 (0.45m0) for the MoSe2 electrons42 (WSe2 holes43).
a Total energy of two trapped IX composed of dipole–dipole repulsion and an attractive harmonic potential (dashed lines) for different confinement lengths. We assume εr = 3 and me/h = 0.8/0.45m0. b Sketch of the interlayer biexciton complex and the coordinate conventions used in the main text. c Schematic illustration of biexciton states with different symmetries of spatial and spin wavefunction. d Binding energy (grey curves) and exchange splitting (red curves) of the trapped biexciton as a function of the confinement length of the harmonic potential. Positive-binding energies correspond to an increase in energy. The grey-shaded (red-shaded) energy range indicates the measured biexciton blueshift (splitting).
The indistinguishability of the two LIX composite bosons forming the biexciton implies that the total wavefunction must be symmetric with respect to IX exchange. This condition can only be satisfied when both spin and spatial parts of the two-exciton wavefunction are simultaneously symmetric or antisymmetric, respectively, as illustrated schematically in Fig. 3c. Thus, the spatial part of the two-IX (biexciton) wavefunction can take the form \(\Psi \sim \frac{1}{{\sqrt 2 }}\left[ {{\it{\uppsi }}_{IX}\left( {\rho _1} \right){\it{\uppsi }}_{IX}\left( {\rho _2} \right) \pm {\it{\uppsi }}_{IX}\left( {\rho _2} \right){\it{\uppsi }}_{IX}\left( {\rho _1} \right)} \right]\), giving rise to two, energetically distinct biexciton states separated by the exchange energy 2J(Δρ). Here, J(Δρ) is given by44
where \(\Psi \left( {x,y} \right)\) is the ground state of Eq. 1 that has been transformed to the coordinate system \(x = \left( {\rho _1 - \rho _2 - {\mathrm{\Delta }}\rho } \right)/\sqrt 2\) and \(y = \left( {\rho _1 + \rho _2} \right)/\sqrt 2\). From this expression, we numerically calculate the exchange splitting to obtain the absolute energies of the two biexciton states:
Here, a positive-binding energy refers to an increase in energy of the biexciton state compared to two isolated excitons. Representative results of our calculations are presented in Fig. 3d that shows the numerically evaluated biexciton binding energy and exchange splitting as a function of the effective confinement lengthscale \(\ell\). The three curves presented on the figure correspond to effective dielectric constants \({\it{\epsilon }} = 2 - 4\). The experimentally observed blueshift of LIX2 of (8.4 ± 0.6) meV is consistent with a confinement lengthscale in the range \(\ell\) = 2.5–3.0 nm, with relatively weak sensitivity to the effective dielectric constant. We interpret the existence of two biexciton states, split by (1.2 ± 0.5) meV, as reflecting the existence of two distinct spatial wavefunctions with even and odd symmetry with respect to IX exchange, as discussed above. The red curves presented in Fig. 3d show the calculated exchange splittings \(J\left( \ell \right)\) for the same range of effective dielectric constants45. The red-shaded region indicates the measured splitting of the biexciton peak. Remarkably, our model calculations simultaneously reproduce both the observed biexciton binding energy and the exchange splitting for a dielectric constant in the range \({\it{\epsilon }} \approx 3\), very close to the average dielectric constant of the environment \({\it{\epsilon }}_{{\mathrm{vac}} - {\mathrm{SiO}_{2}}}\;=\;2.5\), and an effective confinement lengthscale of \(\ell\) ⪅ 3 nm. Thus, we conclude that the strain-induced trapping potentials in the vicinity of the nanopillars give rise to nanometer-scale confinement traps in which the LIX interact via direct and exchange Coulomb interactions.
Figure 2c also shows that the triexciton (LIX3), quadexciton (LIX4) and quintexciton (LIX5) transition lines are even more strongly blueshifted from LIX1, as compared to LIX2. We measure blueshifts of (12.4 ± 0.4) meV for LIX3, (15.5 ± 0.6) meV for LIX4 and (18.2 ± 0.8) meV for LIX5. We extended our calculations for binding energies based on dipole–dipole repulsion in the harmonic trap to three to five excitons (see Supplementary Note 11). The total energy is minimized by maximizing the equilibrium spacing between the particles within the confinement potential. Thus, the IXs in LIX3 (LIX4/LIX5) would be expected to be located at the corners of an equilateral triangle (square/regular pentagon) centered around the trap minimum. We find that independent of the system parameters (e.g. dipole moment d or confinement length \(\ell\)) the blueshift of the LIX3 (LIX4/LIX5) is expected to be about 1.36 × ΔELIX2 (1.92 × ΔELIX2/2.53 × ΔELIX2), where ΔELIX2 is the localized biexciton blueshift. Remarkably, the experimentally observed shifts amount to (1.48 ± 1.12) × ΔELIX2 ((1.85 ± 0.15) × ΔELIX2, (2.17 ± 0.18) × ΔELIX2), respectively, in excellent agreement with this simple prediction.
In summary, we have directly probed interactions between a discrete number NIX = 1–5 of interlayer excitons moving within a localized trapping potential. Power-dependent measurements allow us to identify different few-body states and, moreover, the observed interactions are found to be all mutually in agreement with a localization lengthscale \(\ell \approx 3\) nm. We reproduce the observed blueshift of the biexciton by (8.4 ± 0.6) meV as well as the observed biexciton fine structure with a splitting of (1.2 ± 0.5) meV in a model including the dipolar and exchange interaction of two IX in a harmonic trapping potential. The relative energies of states with one to five trapped IXs are well captured by our model, which predicts maximal spacing of the IXs within the limitations of the trapping potential. The significant interaction energies observed in this paper suggest that strongly correlated multiexciton phenomena, such as Wigner crystallization, may be realized in layered van der Waals heterostructures, opening up new avenues for nonlinear coherent optical control and spin-optronics with interlayer excitons.
After preparation and submission of the paper, we became aware of similar results by another group46.
Methods
Sample fabrication
We fabricated the sample on a Si-[100] wafer with a 285 nm thick SiO2 layer on top. We defined the pillar grid via electron beam lithography on a negative resist (AR-N 7520.07) and etched it into the substrate using F-based reactive ion etching. The pillars have a diameter and height of ~130 nm and ~90 nm, respectively. We exfoliated crystals of WSe2 and MoSe2 (hqgraphene.com) onto polydimethylsiloxane (PDMS, Gel-Pak) stamps, identified monolayers in an optical microscope via reflectivity contrast and then subsequently transferred the WSe2 and MoSe2 using a mask aligner in a cleanroom environment. Each transfer was followed by an annealing step in vacuum (200 °C, 30 min after the WSe2 transfer; 150 °C, 20 min after the MoSe2 transfer which completed the heterostructure). During assembly of the HBL, we took efforts to orientate the crystal axes of the two materials by aligning long crystalline edges of the monolayers.
Optical spectroscopy measurements
Photoluminescence measurements were carried out in two different setups designed for low-temperature confocal microscopy. The data from Fig. 1 were acquired at a setup using a liquid-He flow cryostat at T = 10 K and a HeNe laser (λ = 633 nm) focused to a diameter of ~1 μm. In order to counteract thermal cycling effects (see Supplementary Note 12), the measurements presented in Fig. 2 were carried out in a setup equipped with a closed-cycle cryostat at T = 4 K. The excitation laser used in this setup was at λ = 532 nm and was defocused due to chromatic aberration in the used objective.
We note that the data presented in Figs. 1f and 2 were both recorded from pillar A, but following thermal cycling of the sample to room temperature. This procedure was typically found to result in a shift of the absolute energy of different groups of sharp-line emission features by approximately ±10 meV. Nevertheless, following each cool-down, the generic form of the group of peaks was retained. Supplementary Figure 5 shows power-dependent μPL spectra recorded from pillar A (from the same measurement as the data presented in Fig. 1f), illustrating how the single sharp emission feature is observed close to 1.292 eV at the lowest excitation power investigated, with additional peaks emerging in the range ~5–30 meV to higher energy as Pex increases.
Data analysis
The emission energies shown in Fig. 2c were extracted from Gaussian fits to the PL spectra. In some power regimes, the large peak overlap combined with the low signal-to-noise ratio hindered proper fitting of the data. For this reason, the PL intensities presented in Fig. 2b were determined by integrating the PL signal in an interval of 0.12 meV around the respective center energies. The only exception is the LIX1 peak for which fitting was possible over the whole power range due to its spectral isolation. The data points for LIX3A and LIX3B in Fig. 2b initially overlapped. Thus, the data for LIX3A was slightly offset for better visibility.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Change history
17 September 2021
A Correction to this paper has been published: https://doi.org/10.1038/s41699-021-00256-7
References
Rivera, P. et al. Observation of long-lived interlayer excitons in monolayer MoSe2WSe2 heterostructures. Nat. Commun. 6, 6242 (2015).
Wang, Y., Wang, Z., Yao, W., Liu, G.-B. & Yu, H. Interlayer coupling in commensurate and incommensurate bilayer structures of transition-metal dichalcogenides. Phys. Rev. B. 95, 115429 (2017).
Nagler, P. et al. Interlayer exciton dynamics in a dichalcogenide monolayer heterostructure. 2D Mater. 4, 025112 (2017).
Rivera, P. et al. Interlayer valley excitons in heterobilayers of transition metal dichalcogenides. Nat. Nanotechnol. 13, 1004–1015 (2018).
Zhang, C. et al. Interlayer couplings, Moiré patterns, and 2D electronic superlattices in MoS2/WSe2 hetero-bilayers. Sci. Adv. 3, e1601459 (2017).
Seyler, K. L. et al. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 567, 66–70 (2019).
Tran, K. et al. Evidence for moiré excitons in van der Waals heterostructures. Nature 567, 71–75 (2019).
Wang, Z. et al. Evidence of high-temperature exciton condensation in two-dimensional atomic double layers. Nature 574, 76–80 (2019).
Sigl, L. et al. Condensation signatures of photogenerated interlayer excitons in a van der Waals heterostack. Preprint at https://arxiv.org/abs/2001.07567 (2020).
Miller, B. et al. Long-lived direct and indirect interlayer excitons in van der waals heterostructures. Nano Lett. 17, 5229–5237 (2017).
Kiemle, J. et al. Hybridized indirect excitons in MoS2/WS2 heterobilayers. Phys. Rev. B 101, https://doi.org/10.1103/PhysRevB.101.121404 (2020).
Jauregui, L. A. et al. Electrical control of interlayer exciton dynamics in atomically thin heterostructures. Science 366, 870–875 (2019).
He, Y. et al. Strain-induced electronic structure changes in stacked van der waals heterostructures. Nano Lett. 16, 3314–3320 (2016).
Branny, A., Kumar, S., Proux, R. & Gerardot, B. D. Deterministic strain-induced arrays of quantum emitters in a two-dimensional semiconductor. Nat. Commun. 8, 15053 (2017).
Palacios-Berraquero, C. et al. Large-scale quantum-emitter arrays in atomically thin semiconductors. Nat. Commun. 8, 15093 (2017).
Branny, A. et al. Discrete quantum dot like emitters in monolayer MoSe2: Spatial mapping, magneto-optics, and charge tuning. Appl. Phys. Lett. 108, 142101 (2016).
Jones, A. M. et al. Optical generation of excitonic valley coherence in monolayer WSe2. Nat. Nanotechnol. 8, 634–638 (2013).
Ross, J. S. et al. Electrical control of neutral and charged excitons in a monolayer semiconductor. Nat. Commun. 4, 1474 (2013).
Wang, G. et al. In-plane propagation of light in transition metal dichalcogenide monolayers: optical selection rules. Phys. Rev. Lett. 119, 047401 (2017).
Zhou, Y. et al. Probing dark excitons in atomically thin semiconductors via near-field coupling to surface plasmon polaritons. Nat. Nanotechnol. 12, 856–860 (2017).
Zhang, X.-X. et al. Magnetic brightening and control of dark excitons in monolayer WSe2. Nat. Nanotechnol. 12, 883–888 (2017).
Chen, S.-Y., Goldstein, T., Taniguchi, T., Watanabe, K. & Yan, J. Coulomb-bound four- and five-particle intervalley states in an atomically-thin semiconductor. Nat. Commun. 9, 3717 (2018).
Ye, Z. et al. Efficient generation of neutral and charged biexcitons in encapsulated WSe2 monolayers. Nat. Commun. 9, 3718 (2018).
Barbone, M. et al. Charge-tuneable biexciton complexes in monolayer WSe2. Nat. Commun. 9, 3721 (2018).
Li, Z. et al. Revealing the biexciton and trion-exciton complexes in BN encapsulated WSe2. Nat. Commun. 9, 3719 (2018).
Stevens, C. E. et al. Biexcitons in monolayer transition metal dichalcogenides tuned by magnetic fields. Nat. Commun. 9, 3720 (2018).
Tongay, S. et al. Defects activated photoluminescence in two-dimensional semiconductors: interplay between bound, charged and free excitons. Sci. Rep. 3, 2657 (2013).
Zhang, S. et al. Defect structure of localized excitons in a WSe2 monolayer. Phys. Rev. Lett. 119, 046101 (2017).
Ceballos, F., Bellus, M. Z., Chiu, H.-Y. & Zhao, H. Ultrafast charge separation and indirect exciton formation in a MoS2–MoSe2 van der waals heterostructure. ACS Nano 8, 12717–12724 (2014).
Ceballos, F., Bellus, M. Z., Chiu, H. Y. & Zhao, H. Probing charge transfer excitons in a MoSe2-WS2 van der Waals heterostructure. Nanoscale 7, 17523–17528 (2015).
Rigosi, A. F., Hill, H. M., Li, Y., Chernikov, A. & Heinz, T. F. Probing interlayer interactions in transition metal dichalcogenide heterostructures by optical spectroscopy: MoS2/WS2 and MoSe2/WSe2. Nano Lett. 15, 5033–5038 (2015).
Laikhtman, B. & Rapaport, R. Exciton correlations in coupled quantum wells and their luminescence blue shift. Phys. Rev. B 80, 195313 (2009).
Amani, M. et al. Near-unity photoluminescence quantum yield in MoS2. Science 350, 1065–1068 (2015).
Li, H. et al. Optoelectronic crystal of artificial atoms in strain-textured molybdenum disulphide. Nat. Commun. 6, 7381 (2015).
Refaely-Abramson, S., Qiu, D. Y., Louie, S. G. & Neaton, J. B. Defect-induced modification of low-lying excitons and valley selectivity in monolayer transition metal dichalcogenides. Phys. Rev. Lett. 121, 167402 (2018).
Zrenner, A. A close look on single quantum dots. J. Chem. Phys. 112, 7790–7798 (2000).
Finley, J. J. et al. Charged and neutral exciton complexes in individual self-assembled In(Ga)As quantum dots. Phys. Rev. B 63, 73307 (2001).
Schinner, G. J. et al. Confinement and interaction of single indirect excitons in a voltage-controlled trap formed inside double InGaAs quantum wells. Phys. Rev. Lett. 110, 127403 (2013).
Iff, O. et al. Substrate engineering for high-quality emission of free and localized excitons from atomic monolayers in hybrid architectures. Optica 4, 669 (2017).
Srivastava, A. et al. Optically active quantum dots in monolayer WSe2. Nat. Nanotechnol. 10, 491–496 (2015).
Bondarev, I. V. & Vladimirova, M. R. Complexes of dipolar excitons in layered quasi-two-dimensional nanostructures. Phys. Rev. B 97, 165419 (2018).
Larentis, S. et al. Large effective mass and interaction-enhanced Zeeman splitting of K-valley electrons in MoSe2. Phys. Rev. B 97, 201407 (2018).
Fallahazad, B. et al. Shubnikovde Haas oscillations of high-mobility holes in monolayer and bilayer: landau level degeneracy, effective mass, and negative comp. Phys. Rev. Lett. 116, 086601 (2016).
Bondarev, I. V. Asymptotic exchange coupling of quasi-one-dimensional excitons in carbon nanotubes. Phys. Rev. B 83, 153409 (2011).
Kylänpää, I. & Komsa, H.-P. Binding energies of exciton complexes in transition metal dichalcogenide monolayers and effect of dielectric environment. Phys. Rev. B 92, 205418 (2015).
Li, W., Lu, X., Dubey, S., Devenica, L. & Srivastava, A. Dipolar interactions between field-tuneable, localized emitters in van der Waals heterostructures. Nat. Mater. https://doi.org/10.1038/s41563-020-0661-4 (2020).
Acknowledgements
We gratefully acknowledge funding from the International Max Planck Research School for Quantum Science and Technology (IMPRS-QST), the DFG Clusters of Excellence MCQST, e-Conversion and NIM, DFG Project FI 947/5-1 SQAM, the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 820423 (S2QUIP), the BMBF Verbundprojekt QLink-X, the German Federal Ministry of Education and Research via the funding program Photonics Research Germany (contract number 13N14846) and the Alexander von Humboldt Foundation. K.M. acknowledges support from the Bavarian Academy of Sciences and Humanities. In addition, we thank Richard Schmidt and his team for very helpful discussions.
Author information
Authors and Affiliations
Contributions
M.K., B.D.G., K.M. and J.J.F. conceived and designed the experiments. M.K. and J.G. prepared the sample. M.K., M.B-G., J.G. and M.M. performed the experiments. M.K. analyzed the data. J.K. modelled the exchange interaction. M.K., K.M. and J.J.F. wrote the paper with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
41699_2020_141_MOESM1_ESM.pdf
Supplementary Information to: Discrete Interactions between a few Interlayer Excitons Trapped at a MoSe2-WSe2 Heterointerface
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kremser, M., Brotons-Gisbert, M., Knörzer, J. et al. Discrete interactions between a few interlayer excitons trapped at a MoSe2–WSe2 heterointerface. npj 2D Mater Appl 4, 8 (2020). https://doi.org/10.1038/s41699-020-0141-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-020-0141-3
This article is cited by
-
Engineering interlayer hybridization in van der Waals bilayers
Nature Reviews Materials (2024)
-
Excitonic devices based on two-dimensional transition metal dichalcogenides van der Waals heterostructures
Frontiers of Chemical Science and Engineering (2024)
-
Quadrupolar–dipolar excitonic transition in a tunnel-coupled van der Waals heterotrilayer
Nature Materials (2023)
-
Harmonic to anharmonic tuning of moiré potential leading to unconventional Stark effect and giant dipolar repulsion in WS2/WSe2 heterobilayer
Nature Communications (2023)
-
Layered materials as a platform for quantum technologies
Nature Nanotechnology (2023)