Origins of genuine Ohmic van der Waals contact between indium and MoS₂

Abstract

The achievement of ultraclean Ohmic van der Waals (vdW) contacts at metal/transition-metal dichalcogenide (TMDC) interfaces would represent a critical step for the development of high-performance electronic and optoelectronic devices based on two-dimensional (2D) semiconductors. Herein, we report the fabrication of ultraclean vdW contacts between indium (In) and molybdenum disulfide (MoS₂) and the clarification of the atomistic origins of its Ohmic-like transport properties. Atomically clean In/MoS₂ vdW contacts are achieved by evaporating In with a relatively low thermal energy and subsequently cooling the substrate holder down to ~100 K by liquid nitrogen. We reveal that the high-quality In/MoS₂ vdW contacts are characterized by a small interfacial charge transfer and the Ohmic-like transport based on the field-emission mechanism over a wide temperature range from 2.4 to 300 K. Accordingly, the contact resistance reaches ~600 Ω μm and ~1000 Ω μm at cryogenic temperatures for the few-layer and monolayer MoS₂ cases, respectively. Density functional calculations show that the formation of large in-gap states due to the hybridization between In and MoS₂ conduction band edge states is the microscopic origins of the Ohmic charge injection. We suggest that seeking a mechanism to generate strong density of in-gap states while maintaining the pristine contact geometry with marginal interfacial charge transfer could be a general strategy to simultaneously avoid Fermi-level pinning and minimize contact resistance for 2D vdW materials.

Introduction

Layered semiconducting transition-metal dichalcogenides (TMDCs) such as MoS₂, WSe₂, and MoTe₂ have been extensively studied for the future development of low-power and high-performance electronic and optoelectronic applications^1,2,3. However, establishing a reliable Ohmic contact between metals and TMDCs remains a critical challenge^4,5. For instance, in reducing the Schottky barrier height (ϕ_SB) for TMDCs, efforts to identify metals with appropriate work functions Φ_metal (e.g. Φ_Sc ≈ 3.5 eV for Sc and Φ_Ti ≈ 4.3 eV for Ti) based on the electron affinity of monolayer (1L) and few-layer TMDCs (e.g. monolayer MoS₂: ${\upchi}_{1{\mathrm{L}}\,{\mathrm{MoS}}_2} \approx$ 4 eV, multilayer MoS₂: ${\upchi}_{{\mathrm{ML}}\,{\mathrm{MoS}}_2} \approx$ 4.3 eV) have not been effective because of the strong Fermi-level pinning (FLP) effect^6,7. While various approaches have been explored to overcome this problem, including molecular doping⁸, tunnel-barrier insertion^9,10, fabrication of graphene contacts^11,12, and TMDC phase changes¹³, recent studies have shown that the formation of an ideal or defect-free metal-TMDC van der Waals (vdW) contact through the transfer of atomically flat metal thin films significantly improves the contact properties^14,15,16. In these advances, it was important to recognize that the conventional thermal evaporation process of metals typically introduces crystalline defects in TMDCs and leads to an uncontrollable ϕ_SB (or FLP) and high contact resistance^7,14. Meanwhile, several groups overcame the challenge and showed that the thermal-evaporation process of indium (In) can lead to clean vdW-type contacts for TMDCs with very low contact resistance values^17,18,19. However, regarding our initial report on the achievement of Ohmic-like three-dimensional (3D) In-2D MoS₂ contact¹⁸, question was raised in that the origins of the low contact resistance through the In–MoS₂ vdW contact are unclear.

Here, we prepare an ultraclean vdW contact between In and MoS₂ using an improved evaporation method, and clarify through extensive transport measurements and computations the nature and origins of Ohmic transport characteristics from In/MoS₂ vdW contacts. We prepare the high-quality vdW In/MoS₂ interface by lowering the temperature (T) of the substrate holder to ~100 K during the metal deposition process and utilizing the relatively low In evaporation T of ~530 °C. The In/MoS₂ interface is then characterized by the transmission electron microscope (TEM) and Raman measurements as well as density functional theory (DFT) calculations. DFT calculations show that in comparison with the Au/MoS₂ counterpart, the In/MoS₂ contact induces an order of magnitude smaller charge transfer, which is consistent with the Raman spectroscopy data. For both mono- and few-layer MoS₂ devices prepared through our approach, we find that the contact resistance decreases with decreasing T from room temperature to T = 100 K and 2.4 K, reaching to 1 kΩ μm and 0.6 kΩ μm, respectively. This behavior indicates the Ohmic-like character at the In/MoS₂ contact and the field emission is the dominant charge transport mechanism at the In/MoS₂ contact. We finally identify from DFT calculations large in-gap states originating from the hybridization between MoS₂ conduction-band-edge and In Fermi-level states, which provides a mechanism to achieve an Ohmic contact in spite of the marginal interfacial charge transfer.

Results and discussion

Characterizations of the ultraclean In/MoS₂ interface

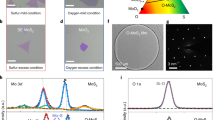
We fabricated MoS₂ field-effect transistors (FETs) on hexagonal boron nitride (h-BN) flakes, where the h-BN flakes were deposited onto a 300-nm-thick SiO₂/Si substrate by mechanical exfoliation. We then transferred a few-layer MoS₂ flake (HQ-graphene, Inc.) onto a selected h-BN flake^12,20. For the electrical measurements, we deposited 100-nm-thick In electrodes across the MoS₂ channel, where the substrate holder was kept at ~100 K by flowing liquid nitrogen through it (see Fig. 1a). The substrate cooling process leads to an important result, namely a highly uniform surface morphology of In film. This contrasts strongly with the usage of a room-temperature holder that produces a segregated granular film for at least up to ~70 nm thickness, as reported in our previous work (also see Supplementary Fig. 1)²¹. The upper panel of Fig. 1b shows a cross-sectional TEM image of the In/few-layered MoS₂ junction, which clearly shows an atomically separated interface between In and MoS₂ layers without any metal invasion into the MoS₂ layers. Whereas crystal-lattice disorders that cause defect-induced gap states and FLP typically occur during the high-temperature deposition process of evaporated metal atoms with high thermal energy^7,14, the In deposited at a relatively low thermal energy could apparently provide a clean vdW interface without disorder or defect. For instance, whereas the evaporation temperature of Au at 10⁻⁷ Torr is ~860 °C, only ~530 °C is required for the evaporation of In at the same pressure. For comparison, we prepared an Au/few-layered MoS₂ junction, where the substrate holder was also kept at ~100 K during Au deposition. The lower panel of Fig. 1b shows a TEM image of the Au/MoS₂ junction, where we observe that the invasion of Au atoms during the deposition process produces atomic defects at the first and second layers from the MoS₂ interface, like previous studies¹⁴.

Fig. 1: Metal deposition on MoS₂.

a In (Au) evaporation in a vacuum chamber with a liquid-nitrogen cooled sample holder. b Top and bottom: cross-sectional TEM images of the In/MoS₂ and Au/MoS₂ interfaces, respectively. Scale bar: 5 nm.

To further characterize the quality of In/MoS₂ interface, we applied the Raman spectroscopy for both the pristine and In-covered MoS₂ regions to estimate doping effect at the metal contacts. It is known that the A_1g phonon peak of MoS₂ exhibits a red shift and its width broadens with electron doping^22,23. Figure 2a, b shows the optical images of, respectively, 1L- and bilayer (2L)-MoS₂ (indicated by regions bounded with dashed black lines) prepared on SiO₂ and partially covered with 5-nm-thick In (indicated by regions bounded with dashed white lines). Figure 2c, d shows the A_1g energy maps for the 1L- and 2L-MoS₂, respectively. The In-covered region shows a relatively lower energy than the non-covered region, i.e., Δω ≈ −0.3 and −1 cm⁻¹ for the 1L- and 2L-MoS₂, respectively (see Supplementary Fig. 2 for representative Raman spectra for a 1L-MoS₂). In the upper panel of Supplementary Fig. 2a, we also show the $E_{2g}^1$ energy map of the 1L-MoS₂, which indicates relatively negligible difference between the In-covered and non-covered regions. For the biaxial strain, the red shift of the $E_{2g}^1$ Raman mode corresponding to the in-plane vibration is more sensitive than the A_1g mode (out-of-plane vibration)^24,25. For the in- and out-of-plane compressive strains, both modes should show blue shifts²⁶. In our case, however, we observed a relatively strong red shift of the A_1g mode than that of the $E_{2g}^1$ mode, which has been interpreted as a doping effect²². For instance, Chakraborty et al.²² reported that the A_1g mode softens with doping at a rate of ~0.2 cm⁻¹ per 10¹² cm⁻² for 1L-MoS₂, whereas the $E_{2g}^1$ mode is relatively insensitive to the doping. We thus conclude that the 1L-MoS₂ region covered by In was doped by electrons at a density of ~+1.5 × 10¹² electrons cm⁻² (electron accumulation in MoS₂). The full-width at half-maximums, Γ, in Fig. 2e, f also show consistent results. For instance, the In-covered region shows a relatively broader Γ than the non-covered region for both 1L- and 2L-MoS₂, implying electron doping. This In-to-MoS₂ electron transfer feature will be further discussed below based on DFT calculations and shown to be another strong indication of ultraclean vdW contacts.

Fig. 2: Raman spectroscopy for In/MoS₂.

a, b Optical images of 1L- and 2L-MoS₂ (dashed black-boxed region) on SiO₂ substrates, respectively. White boxed regions: 5-nm-thick In-deposited regions. Scale bar: 5 μm. c, d A_1g energy (ω) maps for 1L- and 2L-MoS₂, respectively. e, f Full-width at half-maximum (Γ) maps of A_1g for 1L- and 2L-MoS₂, respectively.

Charge redistribution at the In/MoS₂ interface

To extract the atomistic information of the In/MoS₂ vdW contact and contrast them with those of the Au/MoS₂ counterpart, we carried out DFT calculations for the vertical In/MoS₂ and Au/MoS₂ interface models and applied several analysis methods^27,28. In Fig. 3a, b top panels, we show the fully optimized In/MoS₂ and Au/MoS₂ contact models, respectively (see details in Supplementary Figs. 3, 4 and Table 1). First, compared to the Au/MoS₂ case, we find in the optimized In/MoS₂ atomic structure negligible structural distortions at the rightmost metal atomic layer (see also Supplementary Fig. 3). As supported by the DFT-estimated binding energy^29,30 as well as the explicit experimental demonstration for the transferred Au electrode¹⁴, Au is a representative metal that forms vdW-type interactions with MoS₂. Accordingly, the comparatively smaller In contact-induced structural perturbations consistently seen in our experiment and simulation indicate that In forms even more ideal vdW interactions with MoS₂ than Au.

Fig. 3: Charge redistribution properties of the In/MoS₂ interface from DFT calculations.

For the a In/MoS₂ and b Au/MoS₂ interface models, (top panels) DFT-optimized atomic geometries, (middle panels) plane-averaged charge density differences $\Delta \bar \rho$, and (bottom panels) total charge transfers Q (bottom) are shown. In the top panels, interfacial charge transfers are overlaid over the atomic structures, with the electron accumulation and depletion regions represented by the red and blue colors, respectively. The isosurface level is 1 × 10⁻³ e Å⁻³. Schematics of the metal and MoS₂ band levels before contact for the c In/MoS₂ and d Au/MoS₂ cases. Dotted lines represent the MoS₂ charge neutrality levels, whose energetic positions with respect to the In and Au Fermi levels E_F result in the In-to-MoS₂ and MoS₂-to-Au interfacial charge transfers.

To quantify this conclusion, we calculated the real-space charge density differences (Δρ) at the metal/MoS₂ interfaces according to

$$\Delta \rho = \rho _{{\mathrm{metal}}/{\mathrm{MoS}}_2} - \left( {\rho _{{\mathrm{MoS}}_2} + \rho _{{\mathrm{metal}}}} \right)$$

(1)

and overlaid the results on the atomic structures in Fig. 3a, b top panels. The plane-averaged $\Delta \bar \rho (z)$ for the In/MoS₂ and Au/MoS₂ contact cases are also presented in Fig. 3a, b middle panels, respectively. A positive (negative) ∆$\bar \rho$ indicates a gain (loss) in electron density, and we find stronger charge redistributions in the Au/MoS₂ contact compared with the In/MoS₂ counterpart. Examining the distribution of $\Delta \bar \rho$ between the surface metal layers and the interfacial S layer ① of MoS₂, we further note that due to the “push-back” effect arising from Pauli repulsion there appear charge-depleted (negative $\Delta \bar \rho$) 2D plane regions close to the metal surfaces (denoted by vertical dotted lines)^28,30.

Using the minimum-$\Delta \bar \rho$ layers as the reference planes (z = 0), we calculated along the MoS₂ direction the position-dependent accumulated interfacial charge transfers according to

$$Q\left( z \right) = \mathop {\int}\nolimits_0^z \Delta \bar \rho (z^\prime )dz^{\prime} ,$$

(2)

and displayed the results in Fig. 3a, b bottom panels. Note that a positive (negative) Q indicates a metal-to-MoS₂ (MoS₂-to-metal) electron transfer upon establishing the metal/MoS₂ interface²⁷. We then find that In induces a marginal electron transfer of +5.0 × 10¹² electrons cm⁻² to MoS₂ (left blue arrow in Fig. 3a bottom panel), which is in good quantitative agreement with the above-described estimate of ~1.5 × 10¹² electrons cm⁻² from Raman measurement (see Fig. 2). The marginal electron transfer leads to a weakened FLP, compared to an Au case. For the Au/MoS₂ case, the direction of charge transfer is reversed (electron depletion in MoS₂), and its magnitude is significantly enhanced to −1.7 × 10¹³ electrons cm⁻² (left blue arrow in Fig. 3b bottom panel). These opposite MoS₂ doping characters of In and Au can be understood in terms of the alignment of the MoS₂ charge neutrality level $\phi _{1{\mathrm{L}}\,{\mathrm{MoS}}_2}^ \ast \approx$ 4.78 eV with respect to the metal work functions Φ_In ≈ 4.1 eV and Φ_Au ≈ 5.1 eV³¹, as schematically shown in Fig. 3c, d, respectively (see Supplementary Figs. 5, 6, and 7).

Electrical properties of a MoS₂ FET

Figure 4a and b shows a photograph of a MoS₂ FET on a 22-nm-thick h-BN flake and schematic for the electrical measurement configuration, respectively. The number of MoS₂ layers was estimated to be six (6L-#1 MoS₂; see Supplementary Fig. 8). The multiple electrodes for the six-layer (6L) MoS₂ flake with different intervals between two neighboring electrodes were designed to measure the contact resistance via the transfer-length method (TLM)¹³, i.e., four FETs with different channel lengths (L₁ = 0.5 μm, L₂ = 1 μm, L₃ = 1.5 μm, and L₄ = 2 μm from the left channel in the region indicated by a dashed box) with a fixed metal contact length (L_c) as 1 μm. Here, the widths (W) of all channels were nearly identical at 2 μm. Figure 4c shows the two-probe conductance as a function of the back-gate voltage (G–V_G) of the L₂-FET with a source–drain voltage (V_SD) of 30 mV at various temperatures. The conductance decreased for negatively increasing V_G and reached zero near V_G ≈ 0 V throughout the investigated temperature range, which indicates that the electrical carriers are electrons. The two-probe conductance increased with decreasing T at a given V_G for V_G > 10 V, i.e., the device exhibited a metallic behavior. However, the opposite behavior was observed near a depletion region of 0 < V_G < 10 V (see the inset of Fig. 4c), representing an insulating character. These behaviors are consistent with the current–voltage (I–V_SD) curves for various V_G values at T = 2.5 K in Fig. 4d. For instance, the I–V_SD curves for V_G > 10 V and 0 < V_G < 10 V show linear and nonlinear characteristics, respectively. We consider that the linearity and non-linearity originate from the field and thermionic emission through a Schottky barrier, respectively. The four-probe measurements for the L₂ channel also showed a similar V_G value for the metal–insulator crossover location (see Supplementary Fig. 9). This result indicates that the transport in the MoS₂ channel near the conduction-band edge also contributes to the crossover behavior, as well as the Schottky barrier. We also extracted the on/off ratio of ~10⁵ and 10³–10⁵ of other monolayer (1L-#1) and 6L (6L-#2) devices, respectively, as shown in Supplementary section 5. The ratios satisfy a condition for logic gate applications. On the other hand, the on-current densities of 1L-#1 MoS₂ and 6L-#2 MoS₂ devices reached ~60 μA μm⁻¹ and ~200 μA μm⁻¹, respectively. The 6L-#2 MoS₂ device also showed a stability against aging at least for 40 days for −1 V < V_SD < 1 V (see Supplementary Fig. 11d).

Fig. 4: Basic electrical properties of a few-layer MoS₂ field-effect transistor.

a Optical image of a 6L-#1 MoS₂ device with multiple In contacts. Scale bar: 5 μm. b Schematic of 6L-#1 MoS₂ device for the transfer length method (TLM). Here, L_c (=1 μm) is the length of contact electrode. The measurement scheme shows the two-probe measurement for the L₂ = 1 μm channel. c Conductance (G) as a function of the back-gate voltage (V_G) at various temperatures. Inset: G–V_G curves near the metal–insulator crossover region. d I–V_SD curves for various V_G at T = 2.4 K. e, f Mobility (μ) as a function of temperature (T) in log scale for 6L and 1L devices, respectively. The red and blue dashed lines in e and f are fitting lines with the relation of $\mu \left( T \right) \propto T^{ - \alpha }$ with α = 2.2 and 1.1 for 6L and 1L devices, respectively.

In Fig. 4e, we show the field-effect mobility (μ) of the 6L-#1 MoS₂ device as a function of T obtained from the two-probe (open squares) and four-probe (closed squares) measurement schemes. The mobility was obtained at the local maximum location in the μ–V_G curves (see Supplementary Fig. 12). For T > 100 K, in both cases, the data were fitted with a relation of $\mu \left( T \right) = \mu _0T^{ - \alpha }$ with α = 2.2 as shown by the dashed red line. This value is close to the expected value for bulk MoS₂ (α = 2.6) with the optical phonon scattering as a dominant scattering mechanism^12,32,33. At room T, μ ~ 50 cm² V⁻¹ s⁻¹ values were obtained for both cases. However, the two-probe and four-probe μ values were saturated with decreasing temperature in the region T < 20 K at 1200 and 3200 cm² V⁻¹ s⁻¹, respectively. The saturation behavior in low-T regions is known to occur when the impurity scattering assumes a dominant role while the phonon-scattering effect is suppressed³⁴. By contrast, the mobility for two different 1L MoS₂ devices (1L-#1 and 1L-#2; see Supplementary Figs. 10c, 13, respectively) displayed in Fig. 4f show a T dependence with α = 1.1 for T > 100 K, which is close to the prediction of the acoustic phonon scattering becoming a dominant scattering mechanism for a monolayer MoS₂ (ref. ³³).

For comparison, we also fabricated MoS₂ devices with In contacts covered with Au, where the sample holder was a copper block prepared without a liquid-nitrogen cooling process. In this case, we found that the reproducibility was not high enough to obtain the consistent Ohmic-like behavior in the I–V_SD curves, confirming the critical role of our substrate cooling technique (see Supplementary Fig. 14).

Schottky barrier height at In/MoS₂ contacts

We evaluated ϕ_SB at the In/MoS₂ interface because this parameter plays a critical role in determining the contact resistance between a metal and a semiconductor⁴. For this purpose, it is necessary to measure the activation energy (ϕ_AE) at the contacts in the thermionic emission region⁶. Here, because the V_G range for the insulating region is larger than that of the 6L-#1 MoS₂ device (see Fig. 4c), we used the 1L-#2 MoS₂ device with the L = 1 μm channel shown in Supplementary Fig. 13a. Figure 5a shows the resulting G–V_G curves for various temperatures obtained by the two-probe measurement. In this case, the crossover V_G between the insulating and metallic regions was located at a relatively higher V_G (~65 V) than that of the 6L-#1 MoS₂ device, as indicated by an arrow. The G values increased with increasing T for T < 130 K at V_G < 65 V and decreased for T > 200 K in the examined V_G range. When the thermionic emission is dominant, the current crossing a metal/2D system is described by the relation

$$I_{\mathrm{d}} = {{A}}^ \ast T^{3/2}{\mathrm{exp}}\left( {\frac{{ - e\phi _{{\mathrm{AE}}}}}{{k_{\mathrm{B}}T}}} \right)\left[ {{\mathrm{exp}}\left( {\frac{{eV_{{\mathrm{SD}}}}}{{\eta k_{\mathrm{B}}T}}} \right) - 1} \right],$$

(3)

where A^* is the Richardson constant, e is the elementary charge, k_B is the Boltzmann constant, and η is the ideality factor that accounts for a lower barrier height due to image charging¹². Figure 5b shows ${\mathrm{ln}}(I/T^{3/2})$ as a function of $1/k_{\mathrm{B}}T$ at V_SD = 0.5 V for various V_G values from 0 V to 70 V with 5 V spacing (from bottom to top). The slopes of ${\mathrm{ln}}(I/T^{3/2})$ $-1/k_{\mathrm{B}}T$ curves are related to ϕ_AE as $\phi _{{\mathrm{AE}}} = V_{{\mathrm{SD}}}/\eta - {\mathrm{slope}}$. After obtaining the slopes corresponding to representative V_SD values, we plotted the slope as a function of V_SD for various V_G (5 V to 70 V with 5 V spacing from bottom to top) to obtain ϕ_AE at V_SD = 0 V, as shown in Fig. 5c. Finally, we plotted ϕ_AE vs. V_G to obtain ϕ_SB, as blue squares in Fig. 5d. Near the depletion region, ϕ_AE is linearly lowered with increasing V_G when the thermally activated transport is dominant and changes its slope when the field-emission transport is accounted at the Schottky barrier. Thus, the crossover point between them occurs when the band flattens, where, the value of ϕ_AE becomes equal to the value of ϕ_SB⁶. To find V_G making the band flat, we plotted two linear blue lines on the blue squares in Fig. 5d. The two curves meet at V_G ≈ 10 V, where the flat band is believed to form, and we estimated ϕ_SB ≈ 7 meV at the corresponding ϕ_AE for the In/MoS₂ (n = 1) contact. In addition, we also obtained a similar value for the L = 1.5 μm channel as indicated by green squares and green fit lines in Fig. 5d (see also Supplementary Fig. 13a). This value is in a similar range obtained from a Co/h-BN contact with a monolayer MoS₂ (ref. ¹⁰). Such a low ϕ_SB at the In/MoS₂ contact could allow the field-emission to play a dominant role for the transport across the In/MoS₂ contact.

Fig. 5: Schottky barrier height at In/MoS₂ contacts.

a G–V_G curves at various temperatures obtained from the L = 1 μm channel of 1L-#2 MoS₂ device, indicated by a dashed box in Supplementary Fig. 13a. b Scattered points: ${\mathrm{ln}}(I/T^{3/2})$ as a function of $1/k_{\mathrm{B}}T$ with V_SD = 0.5 V from V_G = 0 V to 70 V with 5 V spacing (from bottom to top) obtained from the L = 1 μm channel. Solid lines: fitting result to obtain slope values for each V_G value. c Scattered points: slope as a function of V_SD for various V_G (5 V to 70 V with 5 V spacing from bottom to top). Solid lines: fitting result to obtain ϕ_AE at V_SD = 0 V for each V_G value. d ϕ_AE as a function of V_G for L = 1 and 1.5 μm channels. The arrow indicates the ϕ_SB (~7 meV) for the 1L-#2 MoS₂ device.

Contact resistance at In/MoS₂ contacts

On the basis of the TLM measurements (see Supplementary Fig. 15) with multiple channels (see Fig. 4a), we extracted the contact resistance (R_cW) as a function of n_e of the 6L-#1 MoS₂ device at representative temperatures; the results are shown in Fig. 6a (solid squares; see also Supplementary Table 2). Here, n_e was estimated from the relation $n_{\mathrm{e}} = \left( {e\mu R_{{\mathrm{sh}}}} \right)^{ - 1}$. We note that, for the consistency, the sheet resistance R_sh as well as mobility μ were obtained from the four-probe data, although R_sh could have been extracted from the TLM method. The obtained contact resistance includes serial resistances of In and Ti/Au electrodes (see supplementary Fig. 16). At a given T, R_cW decreased with increasing n_e. The contact resistance is given by^4,5

$$R_{\mathrm{c}}W(n_{\mathrm{e}},T) = \sqrt {R_{{\mathrm{sh}}}(n_{\mathrm{e}},T)\rho _{\mathrm{c}}(n_{\mathrm{e}},T)} ,$$

(4)

which is only valid for L_c≫L_T. Here, ρ_c is the specific contact resistivity and L_T (= $\sqrt {\rho _{\mathrm{c}}/R_{{\mathrm{sh}}}}$) is the transfer length, which represents the average distance that charge carriers flow in a semiconductor beneath the contact before they completely transport to the electrode. Supplementary Fig. 15c shows that our device satisfied this condition with L_c ≈ 1 μm and L_T ≈ 0.1 μm. Equation (4) implies that R_cW decreases with increasing n_e because both R_sh and ρ_c generally decrease with increasing n_e. At a fixed n_e, the thermionic emission charge transport mechanism across the Schottky barrier predicts that R_cW will increase with decreasing T because the thermionic emission will be suppressed with lowering T³⁵. On the other hand, R_cW in our measurements decreased with decreasing T, as shown by scattered red diamonds in Fig. 6b for the case measured at n_e = 3.4 × 10¹² cm⁻². The contact resistance decreased from 2.3 to 0.6 kΩ μm when T was decreased from room temperature to 2.4 K. This behavior, which has been reported in several previous works such as graphene/MoS₂ (ref. ¹²) and Pd/graphene contacts³⁶, is considered as an evidence for the non-dominant role of thermionic emission for the transport across a contact. Scattered squares in Fig. 6b also show R_sh as a function of T at n_e = 3.4 × 10¹² cm⁻², where R_sh decreased with decreasing T because the phonon scattering is reduced.

Fig. 6: Contact resistance with carrier density at In/MoS₂ contacts.

a Contact resistance (R_cW) as a function of carrier density (n_e) of 6L-#1 MoS₂ device at various temperatures (scattered solid squares) with other works (solid curves: graphene(Gr)/4L-MoS₂, opened diamonds: Au/4L-MoS₂, opened pentagons: Au/In/few L-MoS₂). b R_cW and sheet resistance (R_sh) of 6L-#1 MoS₂ device as a function of T at n_e = 3.4 × 10¹² cm⁻².

Sheet resistance vs. specific contact resistivity

We further analyzed the mechanism of charge transport across In/MoS₂ contacts with experimental data in detail. We first examined which component between R_sh and ρ_c predominantly determines the contact resistance of the In/MoS₂ contact. For comparison, we included in Fig. 6a other values reported in the literature; graphene(Gr)/four-layer (4L)-MoS₂ contact¹², Au/4L-MoS₂ (ref. ³⁵) and Au/In/few-layer MoS₂ (ref. ¹⁷). In the case of Gr/4L-MoS₂, the graphene functions as a work-function-controllable contact material, which leads to a lower contact resistance, i.e., R_cW ≈ 1 kΩ μm at n_e > 4 × 10¹² cm⁻² and T = 12 K (see the red curve in Fig. 6a). Although both the Gr-and In-contact MoS₂ devices gave a similar minimum R_cW at cryogenic temperatures, we conclude that the transport mechanisms at the contacts rather differ from each other. For the In/MoS₂ contact case, R_cW decreased with decreasing T in the examined n_e range, representing the field emission (or tunneling) for all examined T and n_e ranges. However, the R_cW−n_e curves obtained at T = 12 and 250 K for the Gr/4L-MoS₂ device suggest that the left and right sides with respect to n_e ≈ 2 × 10¹² cm⁻² followed the thermionic and field emissions at the contact, respectively. At T = 12 K for the Gr/4L-MoS₂ device, although the R_cW of ~1 kΩ μm was relatively insensitive to the variation of n_e in the range from 4 × 10¹² to 7 × 10¹² cm⁻², it rapidly changed from 1 kΩ μm to 6 kΩ μm when n_e decreased from 3 × 10¹² cm⁻² to 1.5 × 10¹² cm⁻². In the case of the Au/4L-MoS₂ contact, on the other hand, R_cW was increased with decreasing T representing the thermionic emission for n_e < 4 × 10¹² cm⁻². While the Au/In/few layer-MoS₂ contact provides a relatively low-R_cW level for n_e > 1.5 × 10¹² cm⁻² at T = 300 K, it is hard to judge the transport mechanism for the In contact because of the absence of the T-dependence of R_cW in the experiment. Then, for the In/6L-#1 MoS₂ device, the R_cW was lowered with decreasing T at a given n_e for 1 × 10¹² cm⁻² < n_e < 1 × 10¹³ cm⁻², representing an Ohmic-like behavior based on the field-emission mechanism in the examined n_e region. In our In/6L-MoS₂ device (see Fig. 7a), R_sh varies in the range from 1 to 80 kΩ when ρ_c only varies from 5 × 10⁻⁶ to 5 × 10⁻⁷ Ω cm², as shown by two dashed lines, for R_cW changing from 0.6 to ~3 kΩ μm. This result indicates that R_sh plays a dominant role in determining R_cW in the field-emission region.

Fig. 7: Contact resistance with sheet resistance at In/MoS₂ contacts.

a Minimum R_cW as a function R_sh of 6L-#1 and 1L-#2 MoS₂ devices at various temperatures (scattered solid squares and stars, respectively) with previous works (opened triangles: graphene(Gr)/4L-MoS₂, opened diamonds: Au/4L-MoS₂, opened pentagons: Au/In/few (1) L-MoS₂). The upper and lower dashed lines were obtained with ρ_c = 5 × 10⁻⁶ Ω cm² and 5 × 10⁻⁷ Ω cm², respectively. b R_cW–T curves for various V_G-th conditions of 1L-#2 MoS₂ device.

We also obtained R_cW from the 1L-#2 MoS₂ device on a 40-nm-thick h-BN flake (see Fig. 7b and Supplementary Fig. 13 for the thickness profile). In Fig. 7b, the R_cW values were extracted via the TLM with three channels (L = 0.5, 1, 1.5 μm) as shown in Supplementary Fig. 13a. For three V_G-th conditions of 35, 40, and 45 V, R_cW decreased with decreasing T in the range 250 ≥ T ≥ 100 K, representing the field emission. Here, V_G−th = V_G − V_th and V_th is a threshold voltage. At V_G−th = 45 V, R_cW reached ~1 kΩ μm at T = 100 K as the minimum value obtained from the 1L-MoS₂ device. Although this value is similar to that obtained from the 6L-MoS₂ device at a similar T range (see Fig. 6a), the contact resistance for the monolayer MoS₂ is higher than that of multilayer MoS₂. The reason could be related to the relatively low affinity energy in the monolayer MoS₂. Interestingly, R_cW increased with decreasing T for T < 100 K under all V_G−th conditions. In this region, the MoS₂ channel also exhibited an insulating behavior in G–V_G curves for various temperatures of Fig. 5a for V_G < 60 V and T < 100 K. Thus, it indicates that the increase of R_sh with decreasing T in the insulating phase plays a dominant role in determining the contact resistance at T < 100 K. We note that this non-Ohmic behavior could not be improved by the contact engineering because the behavior originates from the intrinsic property of MoS₂ itself. This implies that the manipulation of the metal-insulator crossover gate voltage could be crucial to get a better contact property in a mono-layer MoS₂ device. In Fig. 7a (see also Supplementary Table 2), we compared the lowest achievable contact resistance as a function of R_sh from previous reports with ours. For the In/MoS₂ device, the contact resistance decreased with decreasing R_sh and reached ~0.6 kΩ μm as the lowest value at R_sh ~ 1 kΩ and T = 2.4 K. At T = 300 K, on the other hand, the Au/In/few layer-MoS₂ device showed the lowest value of ~0.6 kΩ μm at R_sh ~ 60 kΩ. In addition, for monolayer cases, our In/1L-#2 MoS₂ contact provided 0.9–4 kΩ μm at R_sh ~ 50 kΩ, which are comparable to those obtained from the Au/In/1L-MoS₂ contact that showed ~3 kΩ μm at R_sh ~ 40 kΩ.

Atomistic origins of the field emission-dominated charge transport across In/MoS₂ contacts

Analyzing the electronic structures of the In/MoS₂ and Au/MoS₂ interfaces obtained from DFT calculations, we finally identify the atomistic mechanisms of the experimentally observed Ohmic-like charge transport behavior. It should be noted that, while there exist in the literature several theoretical studies that examined the Schottky barriers in metal/TMDC interfaces^{30,37,38,39,40}, the In/TMDC case has been rarely treated⁴¹. We show the calculated band structures at the In/MoS₂ and Au/MoS₂ contacts in Fig. 8a, b, respectively, and particularly display the projected bands of Mo-4d (green circles in Fig. 8a, b), In-5p_z (wine filled circles in Fig. 8a), and Au-6s (orange circles in Fig. 8b) orbitals. From the band structures, one could determine the electron ϕ_SB by measuring the energy level difference between the conduction band minimum (CBM) edge (upper solid purple line) and the Fermi level E_F (dashed purple line) of metal/MoS₂ contacts. However, the comparison of the two bands indicate that identifying the electron ϕ_SB in the In/MoS₂ contact is a non-trivial matter due to the strong density of in-gap states appearing below and around the MoS₂ CBM region (green circles between CBM and E_F in Fig. 8a; note the absence of such in-gap states in the Au/MoS2 contact in Fig. 8b). To circumvent this difficulty, we first extracted the hole ϕ_SB from the In/MoS₂ junction band structure (see also Supplementary Fig. 5). Next, calculating the band structure of the pristine monolayer MoS₂ using the simulation cell of the corresponding In/MoS₂ junction model (Supplementary Fig. 6), we determined the electron ϕ_SB by subtracting the hole ϕ_SB from the calculated band gap of monolayer MoS₂ (1.94 eV) (Supplementary Fig. 7). The obtained electron ϕ_SB values were 0.31 eV and 0.72 eV for the In/MoS₂ and Au/MoS₂ junctions, respectively. The In/MoS₂ electron, ϕ_SB value of 0.31 eV is comparable to a previous estimate of 0.47 eV⁴¹ and much larger than the experimentally identified marginal ϕ_SB values. We thus conclude that the experimentally observed ϕ_SB is an effective ϕ_SB that has been significantly reduced from the intrinsic ϕ_SB by strong density of in-gap states.

Fig. 8: Atomistic origins of the field emission-dominated charge transport across In/MoS₂ contacts.

Projected band structures of the Mo-4d states (green-filled circle) for the a In/MoS₂ and b Au/MoS₂ interfaces. Shown together in c and d are the In-5p_z (pink filled circles) and Au-6s states (orange filled circles) contributions, respectively. The circle size is proportional to the weight of the projection of the wavefunctions. The PDOS of the In-5p_z (top left panel) and Au-6s (bottom left panel), ① metal-contacting S-3p (second panels), ② Mo-4d (third panels), and ③ outer S-3p (fourth panels) orbitals. In the second, third, and fourth panels, the upper and lower solid lines indicate the MoS₂ CBM and VBM levels, respectively. The arrows schematically show that the charge transport across the In/MoS₂ contact is much more efficient than that across the Au/MoS₂ counterpart, and the Ohmic-like charge transport is mediated by the large in-gap states formed around E_F of the In/MoS₂ interface. The local DOS in the range between E_F and E_F+0.2 eV overlaid over the e In/MoS₂ and f Au/MoS₂ interface models. The iso-surface level is 2.5 × 10⁻⁴ states eV⁻¹ Å⁻³.

Having been identified as the distinguishing feature, the large in-gap states arising in the In/MoS₂ contact should be the source of the marginal effective ϕ_SB and Ohmic-like transport and deserve further attention. Disregarding this factor, for example, can lead to the conclusion that Au would form a better contact than In for MoS₂⁴¹, but the in-gap states of the In/MoS₂ contact remains unexplored^37,38. To examine the nature of in-gap states in the In/MoS₂ interface in comparison with that of the Au/MoS₂ counterpart, we show in Fig. 8c, d how the In-5p_z (pink filled line) and Au-6s (orange filled line) projected density of states (PDOS) evolve into the metal-contacting ① S-3p layer, ② Mo-4d layer, and ③ the outer S-3p layer PDOS of MoS₂ for the In/MoS₂ and Au/MoS₂ contacts, respectively. It is immediately notable that, while the Au-6s PDOS are uniformly distributed across the MoS₂ bandgap (Fig. 8d first panel), the In-5p_z PDOS show energetically very asymmetric distribution such that they start from a negligible level near the MoS₂ VBM region and increase significantly toward the MoS₂ CBM region (Fig. 8c first panel). The MoS₂ VBM and CBM PDOS are mostly composed of Mo-4d orbitals (compare the second/fourth panels with the second panels in Fig. 8c, d). Then, we find for the In/MoS₂ contact case that very strong density of in-gap states are formed between E_F and MoS₂ CBM position (Fig. 8c third panel). As schematically depicted by the thick arrow in Fig. 8c, electrons injecting from In into these MoS₂ in-gap states then should result in the experimentally observed field-emission-type charge transport accompanied by a negligible effective ϕ_SB. On the other hand, the corresponding Mo-4d PDOS around E_F for the Au contact case are relatively marginal, making such a charge injection mechanism ineffective (schematically represented by a thin arrow in Fig. 8d). In Fig. 8e, f, we additionally visualized in real space the E_F-region In-MoS₂ and Au-MoS₂ hybridized DOS, respectively. The stronger hybridization between In and MoS₂ states than that between Au and MoS₂ states then provides an intuitive explanation how the Ohmic-like charge transport is achieved for the In/MoS₂ interface in spite of the very small interfacial charge transfer (see Fig. 3).

In summary, carrying out a combined experimental and theoretical investigation for an ultraclean vdW contact between an elemental metal In (without alloying) and semiconductor MoS₂, we revealed the mechanism of Ohmic charge transport across the In/MoS₂ vdW interface. For the single- and few-layer MoS₂ devices, the contact resistance decreased with decreasing temperatures for 100 ≤ T ≤ 300 K, indicating the field-emission mechanism for the Ohmic-like contact transport. The contact resistance was sensitive to the change of sheet resistance of MoS₂, rather than that of the specific contact resistivity within the field-emission region. For the monolayer MoS₂ case, we achieved the contact resistance of ~1 kΩ μm at T = 100 K, which is the lowest value achieved by metal evaporations on MoS₂ to date. Our experimental findings were corroborated by DFT calculations, which showed that the In/MoS₂ contact has a weakened FLP due to the marginal interfacial charge transfer. Importantly, in spite of the weak interface dipole formation, we found that strong density of in-gap states are formed around MoS₂ CBM states and enable an Ohmic-like charge transport across the In/MoS₂ interface. Related with this identified mechanism, we comment that one of us previously predicted for semiconducting carbon nanotubes that a highly efficient charge injection across vdW metal contacts could be achieved via large in-gap states generated from topological defects within the sp² carbon network²⁸. We thus suggest that seeking a mechanism of introducing strong density of in-gap states while maintaining the ideal contact geometry with weak charge transfer could prove to be a general strategy to simultaneously avoid FLP and minimize contact resistance for low-dimensional vdW materials⁴².

Methods

Device fabrication

We fabricated MoS₂ FETs on h-BN flakes, where the h-BN flakes were deposited onto a 300-nm-thick SiO₂/Si substrate by mechanical exfoliation. We then transferred a few-layer MoS₂ flake (HQ-graphene, Inc.) onto a selected h-BN flake^12,20. For the electrical measurements, we deposited 100-nm-thick In electrodes across the MoS₂ channel, where the substrate holder was kept at ~100 K by flowing liquid nitrogen through it. The substrate cooling process leads to an important result; a uniform surface morphology of In film is achieved, which contrasts strongly with the usage of a room-temperature holder that produces a segregated granular film for at least up to ~70 nm thickness, as reported in our previous work (also see Supplementary Fig. 1)²¹.

Raman spectroscopy

The Raman measurements were performed in a backscattering geometry at room temperature. An incident laser light with a wavelength of 514.5 nm was focused on the sample surface through an optical microscope objective lens (100×/0.9 NA). An excitation laser power was maintained less than 0.4 mW to avoid any laser-induced heating effects. Scattered light from the sample was dispersed through a monochromator with a 1200 grooves mm⁻¹ grating and was collected using a thermoelectrically cooled charge-coupled device detector. For mapping measurements, Raman spectra were taken at the step of 0.5 μm over the area of 15 × 15 μm².

DFT calculations

We performed DFT calculations within the local density approximation (LDA)⁴³ using the SIESTA software⁴⁴. The atomic cores were replaced by norm-conserving nonlocal pseudopotentials of the Troullier-Martins type⁴⁵, and double ζ-plus-polarization-level numerical atomic orbital basis sets were employed. Geometry optimizations were performed until the Hellmann-Feynman ionic forces were below 0.02 eV Å⁻¹_. To check the reliability of geometries and electronic structures obtained within LDA in terms of vdW interactions, we also carried out DFT calculations using the DFT-D3 (ref. ⁴⁶) exchange-correlation functional. As in our earlier work⁴⁷, we obtained consistent results from LDA and DFT-D3 calculations (see Supplementary Figs. 3, 4 and Table 1).