Abstract
Machine-learning techniques enable recognition of a wide range of images, complementing human intelligence. Since the advent of exfoliated graphene on SiO2/Si substrates, identification of graphene has relied on imaging by optical microscopy. Here, we develop a data-driven clustering analysis method to automatically identify the position, shape, and thickness of graphene flakes from optical microscope images of exfoliated graphene on an SiO2/Si substrate. Application of the extraction algorithm to optical images yielded optical and morphology feature values for the regions surrounded by the flake edges. The feature values formed discrete clusters in the optical feature space, which were derived from 1-, 2-, 3-, and 4-layer graphene. The cluster centers are detected by the unsupervised machine-learning algorithm, enabling highly accurate classification of monolayer, bilayer, and trilayer graphene. The analysis can be applied to a range of substrates with differing SiO2 thicknesses.
Similar content being viewed by others
Introduction
Machine learning enables the extraction of meaningful patterns from examples,1 which is one of the traits that characterize human intelligence. Attempts to automate scientific discovery using machine learning have been rapidly increasing in number,2 and their advantages have been demonstrated in various research fields such as biology,3,4,5 medicine,6,7 and physics.8,9,10,11,12 Across all domains, the success of machine-learning methods has been most prominent in image analysis.13,14,15 In the context of cell biology, automated optical microscopy has been acquiring high-quality cellular images on an unprecedented scale,16 thus processing large-scale image collections and enabling researchers to automatically identify cellular phenotypes.3 In medical image processing, deep-learning technologies are opening up new avenues for the automated diagnostics of various types of diseases.7
In research fields concerning two-dimensional (2D) materials, the recent development of robotic automation has enabled the autonomous search for 2D crystals and subsequent assembly of the 2D crystals into van der Waals superlattices.17 The robotic assembly of van der Waals heterostructures has suggested the possibility for high-throughput production of complicated van der Waals heterostructures. Besides these functionalities, the system provides an opportunity for collecting optical microscope images of the exfoliated 2D crystals on SiO2/Si substrates in a large scale. When graphene flakes are exfoliated onto SiO2/Si substrates using the scotch tape method,18 the graphene flakes of various thicknesses and shapes are randomly distributed over the SiO2/Si substrates. If the images of the entire region of SiO2/Si substrates with exfoliated graphene are collected, the image dataset must contain a sufficiently large number of n-layered graphene flakes, where n = 1, 2, 3, and so on. Therefore, a large set of SiO2/Si images can provide an unprecedented level of information for developing automated segmentation and a classification algorithm for exfoliated graphene flakes using data-driven analysis and machine-learning algorithms.
In general, machine learning algorithms are classified into two categories:1,19 supervised learning, in which a human operator annotates a part of the data to train the models, thereby constructing a model that classifies the rest of the data,20 or unsupervised learning, in which patterns in the data such as the clusters are detected from the unlabeled data. Since the advent of monolayer graphene on SiO2/Si substrates,18,21 the identification process of the graphene flakes has relied on the recognition of graphene on SiO2/Si substrate by the human operator. The parameter tuning process for detecting graphene flakes on SiO2/Si substrates was necessary for the automated searching system of graphene flakes.17 By developing a method based on unsupervised learning, it can eliminate the identification process, ambiguity in the layer thickness determination, and the parameter tuning process.
In this report, we present an unsupervised data-driven analysis method to classify graphene layers using a large set of optical microscope images. By processing ~7 × 104 images of SiO2/Si substrates with exfoliated graphene, we extracted ~4 × 105 segmented regions enclosed by edges. The optical and morphological feature values were extracted from the segmented regions. Plotting the data points in the hue (H), saturation (S), and value (V) space resulted in discrete clusters. Analyzing the data points revealed that the clusters are derived from n-layered graphene, where n = 1, 2, 3, and so on. An unsupervised machine-learning clustering algorithm based on a non-parametric Bayesian mixture model can detect cluster centers, and they can classify graphene layers with high accuracy (>95%). These results demonstrate that identification of graphene layers can be performed by computational methods,1,19 thus introducing new routes for utilizing data-driven methods for the identification of graphene layers and determination of the layer thickness.
Results
Label-free analysis workflow
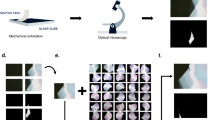
The first step in the workflow of automated graphene classification was to capture optical microscope images of entire exfoliated graphene flakes on the SiO2/Si substrate (Fig. 1a). Twenty-four SiO2/Si substrates with the size of 1 × 1 cm2 with exfoliated graphene flakes were tiled onto the silicon chip tray and were scanned by the automated optical microscope.17 Two types of SiO2/Si substrates with different SiO2 thicknesses of d ~ 290 and 85 nm22 were used to demonstrate the generality of the image analysis pipeline. The images were acquired using a CMOS camera capable of capturing images in high bit depth (12-bit), which enables accurate detection of the edge patterns. The data were stored in a large-scale storage, comprising a large number of raw optical microscope images of ~1 TB. The images were then processed by the feature extraction algorithm (see Methods and Supplementary Figure 1). The algorithm detects the regions enclosed by the edges. The third panel of Fig. 1a shows the representative output of the segmentation algorithm applied to the image containing exfoliated graphene flakes. The segmented areas were indicated by the colored regions in the third panel of Fig. 1a. The process was performed without assuming the specific color value of the monolayer, bilayer, and trilayer graphene flakes in advance. By utilizing the extracted regions as the masks to the images, ~50 types of feature values were extracted from each region (summarized in Supplementary Table 1).23 The extracted feature values were categorized into three classes: morphology, optical intensity, or positions. By applying the data analysis pipeline to the ~7 × 104 images of SiO2/Si with exfoliated graphene layers, ~105 regions were detected and ~107 feature values were extracted. At least 3–4 SiO2/Si substrates were required to perform the clustering analysis (Supplementary note 1). We analyzed the feature values using the data analytics frameworks Pandas, Matplotlib, Jupyter notebook, and Scikit-learn (see Methods).
Data-driven analysis workflow and raw scatter plots of extracted feature values. a Schematic of data analysis workflow. First, the optical microscope images of the SiO2/Si substrate are acquired using the automated optical microscope. The acquired images are fed into the feature extraction pipeline. The segmented region surrounded by the optical edges are applied to the image, generating ~50 feature values from each region (Supplementary Table 1). The extracted feature values are analyzed by the data analysis methods. Since each data point is linked to the optical microscope images, the corresponding images can be investigated in the preceding process. b–d The scatter plots of the feature values: b Sarea vs. IH, c Sarea vs. IS−BG, and d Sarea vs. IV−BG
Figure 1b–d show the scatter plots of the area Sarea and the optical feature values extracted from the regions in the HSV color space IH, IS−BG, and IV−BG. As the values of optical features, we utilized the medians of the optical intensities in the HSV color space IH, IS, and IV, respectively. Here, in order to compensate for the unequal illumination of the field, we extracted the medians of the optical intensities of the bare SiO2/Si substrates without exfoliated graphene IS,BG and IV,BG, and the background values were subtracted for the S and V color spaces as IS−BG = IS − IS,BG and IV−BG = IV − IV,BG. The background subtraction was not applied for the hue color space. The point of note here is that discernible stripe patterns emerged in the IS,BG and IV,BG plots, as indicated by the black arrows in the Fig. 1c, d. The most prominent stripe was located at IV−BG = 0, and the other stripes were sequenced from the stripe and were equally spaced.
Three-dimensional representation of the feature values
To capture the features of the stripe patterns shown in Fig. 1c, d in detail, we visualize the data points in the three-dimensional parameter space of the optical feature values \(\left( {I_{\mathrm{H}},I_{{\mathrm{S}} - {\mathrm{BG}}},I_{{\mathrm{V}} - {\mathrm{BG}}}} \right)\) in Fig. 2a. Here, the area values of the feature parameters of Sarea are represented by the sizes of each data point, and they linearly scale with Sarea. According to this representation, discrete clusters were formed as indicated by the black arrows in Fig. 2a. For descriptive purposes, we labeled the clusters A–E [Fig. 2a]. The cluster A is located at IS−BG = 0 and IV−BG = 0. The clusters B–E are equally spaced in the direction of IV−BG. Based on these observations, we attribute the stripe patterns emerged in Fig. 1c, d to the clusters A–E in Fig. 2a. These clusters emerged simply on applying the feature extraction algorithm to the large set of optical microscope images. Therefore, the presented clustering results are expected to be robust against the changes in the experimental parameters. To explore the generality of the image analysis pipeline, we applied the same algorithm to the optical microscope images of SiO2/Si substrates with a thickness d = 85 nm. As shown in the Fig. 2b, discrete clusters similar to Fig. 2a emerged in this case, as well, as indicated by the black arrows labeled Aʹ–Eʹ. These results demonstrate the generality of the clustering results of the feature values extracted from the optical microscope images in the three-dimensional color space of (IH,IS−BG,IV−BG).
Three-dimensional scatter plot of optical feature values. a,b Scatter plot of feature values IH, IS−BG, and IV−BG for the SiO2 thickness of d = a 290 nm and b 85 nm. The size of each data points is scaled by the area of region Sarea. The clusters are marked by black arrows and are labeled as A–E and (Aʹ–Eʹ) for d = 290 and 85 nm, respectively
Histogram analyses of the extracted features
To quantitatively explore the characteristics of the clusters in Fig. 2a in detail, we focus on the projection of the three-dimensional plot in Fig. 2a to the IV−BG and IH space, and we assemble the feature values of Sarea to produce a cumulative histogram as a function of IV−BG and IH, as shown in Fig. 3a. For clarity, we show the one-dimensional cumulative histogram of Sarea for IH < 1.6 and 2.25 < IH. When represented in this form, the clusters A–E shown in Fig. 2a were embedded into island-shaped discrete clusters, shown by white arrows in Fig. 3a. The clusters B–E were sequenced in the counter-clockwise direction originating from cluster A. For the regions beyond cluster E, the boundary between the clusters gradually became obscure. Finally, the area histograms formed ridge structures in the region of 2 < IH. The positions of the island-shaped clusters were also visualized by multiple peak structures in the one-dimensional histogram for IH < 1.6 (the black arrows in Fig. 3b). To describe the ridge structure, we labeled the ridge appearing for 2.25 < IH as F (Fig. 3a, c).
Two-dimensional cumulative histogram of area plotted in the optical value space. a Two-dimensional color plot of the cumulative histogram Sarea as a function of IV−BG and IH. The clusters are indicated by white arrows. b,c Cumulative histogram of the area Sarea as a function of IV−BG for b IH < 1.6. and c 2.25 < IH
Inspection of the clusters
To investigate the origins of the clusters, we manually defined the borders in Fig. 3a, so that each group contained the clusters A–E, as (i) −0.02 < IV−BG < 0.02, (ii) −0.055 < IV−BG ≤ −0.02, (iii) −0.09 < IV−BG≤−0.055, (iv) −0.12 < IV−BG ≤ 0.9, and (v) −0.15 < IV−BG≤0.12 and for IH < 1.6 [indicated by the purple squares in Fig. 3a]. For the ridge structure F, we defined the group (vi) as −0.4 < IV−BG < 0.02 and for IH > 2.25 [The purple square in Fig. 3a]. To investigate the optical microscope images belonging to the groups, we sampled data points from groups that had the areas larger than the threshold value Sarea > 500. In Fig. 4a, we show the representative optical microscope images from the groups (i)−(vi) (from top to bottom). The red square marks in Fig. 4a indicate the centers of segmented regions. In group (i), the segmented region centers were located at the surface of SiO2/Si substrates (red squares in the top row of Fig. 4a). Manual inspection of all images indicated that 84% of the images resulted from SiO2/Si substrates. Since the segmented regions tend to be surrounded by contaminating objects such as scotch tape residues, the origins of the cluster A can be attributed to the bare SiO2/Si substrates accidentally surrounded by optical edges. This observation is consistent with the values of IV−BG=0 and IS−BG=0 obtained for optical features. In the case of group (ii), the segmented regions were mostly derived from monolayer graphene flakes (the second row of Fig. 4a). Similarly, the groups (iii)−(v) were mostly derived from bilayer, trilayer, and tetralayer graphene flakes (third, fourth, and fifth rows of Fig. 4a, respectively). Finally, the inspection of the region (vi) reveals that the group (vi) was derived from thick graphite flakes (sixth row of Fig. 4a).
Optical microscope images extracted from regions (i)–(vi) and their confusion matrix. a Optical microscope images extracted from groups (i)–(vi) (top to bottom). The images are randomly sampled from each group by applying the thresholds Sarea > 500 pixels. The red diamond mark indicates the center of the segmented region detected by the image processing algorithm. Each scale bar corresponds to a length of 5 μm. b Confusion matrix of the data points obtained by manually inspecting all the optical microscope images with Sarea > 500 pixels. The numbers are represented in units of %, except for the total column which indicate the number of inspected optical microscope images
To quantitatively evaluate the contents of the regions (i)–(vi), we manually inspected all the optical microscope images that exhibited a value of Sarea > 500 pixels in the defined regions (i)–(vi) and created a confusion matrix of the classes as presented in Fig. 4b. In Fig. 4b, the column on the far left indicates groups (i)–(vi), and the top row indicates labels annotated by the human operator. The representative optical microscope images of the misclassifications (Fringes, Peeled, and Particles) are presented in the Supplementary Figure 2. According to the investigation, 82.7% of data points in group (ii) were due to monolayer graphene, whereas the remaining data points were attributable to contaminating objects such as fringes, peeled flakes, and particles. Similarly, 91.9% and 90.5% of the data points in the groups consisted of bilayer and trilayer graphene flakes. Based on these observations, we can conclude that the clusters B–D in Fig. 3 were derived from monolayer, bilayer, and trilayer graphene flakes. These clustering results were obtained only by processing a large number of optical microscope images of SiO2/Si substrate without prior knowledge about the specific color contrast of graphene. This result thus demonstrates the highly generalizable approach for automatically classifying the graphene layers on SiO2/Si substrates.
Unsupervised machine-learning clustering analysis
Since the image processing algorithm successfully extracted the feature values of the graphene flakes, the next step is to introduce the probabilistic unsupervised machine learning algorithm to automate detection of cluster centers and improve the classification accuracy. To model the optical feature values of graphene flakes, we utilized the mixtures of Gaussians for the pixel intensities. The application of the Gaussian mixture model is appropriate because the color contrast of the exfoliated graphene flakes changes discretely with their nature22 and the obscuring effects of the pixel intensities can be treated by the Gaussian distribution. A similar Gaussian mixture-based technique was utilized in the segmentation of brain magnetic resonance images.24,25 Here, the frequencies of the pixels of the hue and value color space \({\boldsymbol{x}}_{\boldsymbol{i}} = \left( {I_{\mathrm{H}}^i,\,I_{{\mathrm{V}} - {\mathrm{BG}}}^i} \right)\) belonging to the class i can be modeled as
where K is the class number, zi∈[1,…,K] is the class label, μk is the mean, Σk is the covariance matrix, πk is the probability of each pixel being classified to the class k. The parameters that need to be optimized to capture the cluster shapes are \({\boldsymbol{\mu }}_k,{\boldsymbol\Sigma }_k,\pi _k,\,{\mathrm{and}}\,K\). The principal problem with the parameter optimization of the mixture models is how to optimize the component number K.19 To solve this issue, we employed the framework of the Bayesian Gaussian mixture model with Dirichlet process (BGMM-DP),19,26 wherein the optimization process involves the cluster number estimation.
Since the BGMM-DP process is computationally intensive, we restricted the analysis parameter space to IH < 1.6 and IV−BG < 0.1 and reduced the number of data points by scaling the area feature values as \(S_{{\mathrm{area}}}^{{\mathrm{sc}}} = S_{{\mathrm{area}}}{\mathrm{/}}400,\) and rounding \(S_{{\mathrm{area}}}^{{\mathrm{sc}}}\) to the nearest integer. Then, the feature vector was composed by concatenating all the pixel values over the detected area as \({\boldsymbol{x}} = \left( {{\boldsymbol{x}}^1,{\boldsymbol{x}}^2,{\boldsymbol{x}}^3, \cdots ,{\boldsymbol{x}}^n} \right)\), where n is the total number of the pixels. In Fig. 5a, we show the results of BGMM-DP optimization by plotting the values of xi and indicating the class types by the colors and the positions of the detected cluster centers μk by the black crosses. The cluster weights \(W_k = \pi _k{\mathrm{/}}\left( {2\pi } \right)\left| {{\mathbf{\Sigma }}_k} \right|\) are represented by the sizes of the black crosses in Fig. 5a. The quantitative representation of weights Wk is shown in Fig. 5b. For clarity, each detected cluster is labeled by one of the letters a–x. The letters are placed for descriptive purpose and their order has no physical meaning. The notable feature observed here, as marked by the black arrows in Fig. 5a, is that the clusters owing to the substrate and monolayer, bilayer, and trilayer graphene flakes have been correctly classified into discrete clusters. These results indicate that the application of the BGMM-DP algorithm to the clustering process of graphene flakes is robust against overfitting and successfully identifies the cluster centers μk and variances Σk of the monolayer, bilayer, and trilayer graphene flakes. In contrast, when optimization is performed using the conventional expectation maximization, they tend to fall into overfitting and the clusters of monolayer, bilayer, and trilayer graphene flakes are not classified correctly (Supplementary Note 2).
Results of unsupervised machine-learning clustering algorithms applied for the feature values. a Clustering results of the Bayesian Gaussian mixture model with the Dirichlet process (BGMM-DP). The cluster centers are indicated by filled crosses. The weights of the clusters are indicated by the sizes of cross marks. b Extracted weights for the clusters of BGMM-DP. c Confusion matrix of the clusters made by manually checking the optical microscope images. The numbers are represented in units of % except for the Total column, which represents the number of inspected images
Finally, to estimate the performance metrics of the clustering based on the BGMM-DP algorithm, we manually checked all the optical microscope images belonging to the clusters a, n, g, and o, with Sarea > 500 and created the confusion matrix of the clusters. The results are presented in Fig. 5c. A high percentage of correct answers (>95%) were achieved for all the monolayer, bilayer, and trilayer graphene flakes. These results demonstrate the high performance of the presented automated classification algorithm. We put emphasis on the result that the high percentage of correct classification was achieved only by processing the optical microscope images in a one-way manner; thus, the optical feature values of monolayer, bilayer, and trilayer graphene flakes were extracted self-consistently from the optical microscope images. These results demonstrate the effectiveness of data-driven and big-data approach for segmenting graphene flakes.
Discussion
Ever since the advent of monolayer graphene,21,27 the identification process of the monolayer, bilayer, and trilayer graphene flakes have relied on the interference color of the SiO2/Si substrate.22 Since the color contrast of atomically thin 2D crystal flakes is sensitive toward the thickness of the SiO2 substrate, which can fluctuate according to the experimental condition, the determination process of the layer thickness depends on the initial guess of the layer number by the human operator. However, the presented method provides quantitative estimation of the optical feature values of graphene flakes without tuning parameters, and their thickness can be self-consistently extracted and represented by the equal spacing of the clusters in the IV direction. Therefore, these algorithms can be utilized for automated determination of graphene layer thickness only using optical microscope images, without the use of the time-consuming spectroscopic tools such as Raman spectroscopy28 or atomic force microscopy.29,30 This method allows researchers to utilize an unlimited number of graphene flakes simply by exfoliating graphite flakes on SiO2/Si substrates and scanning them using automated optical microscopy.
The future perspective is to develop a universal classification algorithm that can work on any material, which could be achieved by analyzing the feature values in the other dimensions not utilized in this work, such as the morphological feature, because in the case of transitional metal dichalcogenides, the small density of exfoliated crystal flakes hinders the formation of discrete clusters in the HSV color space. For the analysis of complicated data in high dimension, feature embedding techniques such as principal component analysis1 or stochastic neighbor embeddings31 could be utilized for mining further information about feature values of exfoliated 2D crystal flakes. This direction of research can be fostered by obtaining data from exfoliated graphene flakes, because the shape features of the exfoliated graphene flakes show many similarities with that of other exfoliated 2D crystals owing to similar crystal structures. Alternatively, application of the rapidly developing deep-learning technology based on convolutional neural networks could be considered. Considering the high performance of convolutional neural networks achieved in medical imaging,7 one could expect high performance in identifying atomically thin 2D crystals.
In summary, this work demonstrated that the current image processing algorithm, the big-data analysis technique, and the unsupervised machine-learning algorithm can successfully segment graphene layers with high accuracy. By integrating the current algorithm to the automated optical microscope in a 2D materials manufacturing system, one can develop a fully automated identification machine of graphene flakes, allowing researchers to utilize unlimited number of graphene flakes simply by exfoliating graphite flakes on SiO2/Si substrates and scanning them using automated optical microcopy. Therefore, this study could be a fundamental step toward realizing fully automated fabrication of van der Waals heterostructures.
Methods
Mechanical exfoliation
SiO2/Si substrates with an approximate size of 1 × 1 cm2 were cleaned using a piranha solution followed by rinsing with ultrapure water. Kish graphite was mechanically exfoliated onto SiO2/Si substrates using the Scotch tape method.
Optical microscope image acquisition
The SiO2/Si substrates were tiled onto the silicon chip tray, which can accommodate up to 36 SiO2/Si substrates. The surface of SiO2/Si substrates were scanned by the automated focus microscope with ×50 objective lens. The optical microscope images were acquired in 12-bit depth TTF format lossless compression (LZW) and stored into the network attached storage capable of storing optical microscope images. The images from 24 SiO2/Si substrates in the approximate size of 1 × 1 cm2 constituted about 1 TB of data.
Feature extraction
Feature extraction was performed using the commercial image processing library HALCON13. The detailed schematics of the feature extraction process can be seen in Supplementary Figure 1. First, the edge-preserving smoothing filter was applied to the loaded image. Then, the image was converted to grayscale. The edges were detected by Canny’s edge detection. The endpoints of the nearest edges were closed by the morphological operation. The regions enclosed by the edges were filled up. The original images were decomposed into HSV color space. The extracted regions were applied as masks to the decomposed HSV images. The optical feature values in the hue, saturation, and value color spaces were normalized to the range of \(I_{\mathrm{H}} \in \left[ {0,\pi } \right],I_{\mathrm{S}} \in \left[ {0,1} \right],\,{\mathrm{and}}\,I_{\mathrm{V}} \in \left[ {0,1} \right]\), respectively, and represented by floating-point values. The position parameters of the exfoliated graphene layers (X, Y) were recorded in the encoder counts of the XY stages. Finally, the feature values listed in Supplementary Table 1 were extracted and stored in CSV format. To accelerate the feature extraction process, we utilized the multithread parallel programming functionalities of HALCON13. The processing of 1 TB of images took 12 h using a 2-CPU workstation with NVIDIA Quadro M4000 graphic processing units.
Data analysis
The feature values were analyzed using the open-source data analytics platforms Python, Jupyter notebook, SciPy, NumPy, Matplotlib, Pandas, and Scikit-learn. We also utilized the Pillow image processing library for cropping and resizing the optical microscope images for data visualization.
Data availability
The data that support the findings of this study are available from the corresponding author upon request. The source code utilized in this work are available at the software code repository (https://github.com/tdmms/tdmms_ml_omimages/).
References
Bishop C. M. Pattern Recognition and Machine Learning (Springer, Berlin, 2006).
King, R. D. et al. The automation of science. Science 324, 85–89 (2009).
Blasi, T. et al. Label-free cell cycle analysis for high-throughput imaging flow cytometry. Nat. Commun. 7, 10256 (2016).
Eulenberg, P. et al. Reconstructing cell cycle and disease progression using deep learning. Nat. Commun. 8, 463 (2017).
Carpenter, A. E. et al. CellProfiler: image analysis software for identifying and quantifying cell phenotypes. Genome Biol. 7, R100 (2006).
Erickson, B. J., Korfiatis, P., Akkus, Z. & Kline, T. L. Machine learning for medical imaging. Radiographics 37, 505–515 (2017).
Litjens, G. et al. A survey on deep learning in medical image analysis. Med. Image Anal. 42, 60–88 (2017).
Kalinin, S. V., Sumpter, B. G. & Archibald, R. K. Big–deep–smart data in imaging for guiding materials design. Nat. Mater. 14, 973 (2015).
Carrasquilla, J. & Melko, R. G. Machine learning phases of matter. Nat. Phys 13, 431–434 (2016).
Wetzel, S. J. Unsupervised learning of phase transitions: from principal component analysis to variational autoencoders. Phys. Rev. E 96, 022140 (2017).
Lemmer, M., Inkpen, M. S., Kornysheva, K., Long, N. J. & Albrecht, T. Unsupervised vector-based classification of single-molecule charge transport data. Nat. Commun. 7, 12922 (2016).
Ramprasad, R., Batra, R., Pilania, G., Mannodi-Kanakkithodi, A. & Kim, C. Machine learning in materials informatics: recent applications and prospects. npj Comput. Mater 3, 54 (2017).
Rivenson, Y. et al. Deep learning microscopy. Optica 4, 2334–2536 (2017).
Chen, C. L. et al. Deep learning in label-free cell classification. Sci. Rep. 6, 21471 (2016).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436 (2015).
Shapiro H. M. Practical Flow Cytometry (A.R. Liss, 1988).
Masubuchi, S. et al. Autonomous robotic searching and assembly of two-dimensional crystals to build van der Waals superlattices. Nat. Commun. 9, 1413 (2018).
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306, 666–669 (2004).
Murphy K. P. Machine Learning: A Probabilistic Perspective (The MIT Press, 2012).
Lin, X. et al. Intelligent identification of two-dimensional nanostructures by machine-learningÿ optical microscopy. Nano Research 11, 6316–6324 (2018).
Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197 (2005).
Blake, P. et al. Making graphene visible. Appl. Phys. Lett. 91, 63124 (2007).
Leemput, K. V., Maes, F., Vandermeulen, D. & Suetens, P. A unifying framework for partial volume segmentation of brain MR images. IEEE Trans. Med. Imaging 22, 105–119 (2003).
Szeliski, R. Computer Vision: Algorithms and Applications (Springer-Verlag, New York, 2010)
Tian, G., Xia, Y., Zhang, Y. & Feng, D. Hybrid genetic and variational expectation-maximization algorithm for Gaussian-mixture-model-based brain MR image segmentation. IEEE Trans. Inf. Technol. Biomed. 15, 373–380 (2011).
Ferguson, T. S. A Bayesian analysis of some nonparametric problems. Ann. Stat. 1, 209–230 (1973).
Zhang, Y., Tan, Y. W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry's phase in graphene. Nature 438, 201–204 (2005).
Ferrari, A. C. et al. Raman spectrum of graphene and graphene layers. Phys. Rev. Lett. 97, 187401 (2006).
Nemes-Incze, P., Osváth, Z., Kamarás, K. & Biró, L. P. Anomalies in thickness measurements of graphene and few layer graphite crystals by tapping mode atomic force microscopy. Carbon 46, 1435–1442 (2008).
Zhang, H. et al. Atomic force microscopy for two-dimensional materials: a tutorial review. Opt. Commun. 406, 3–17 (2018).
van der Maaten, L. & Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605 (2008).
Acknowledgements
The authors would like to thank M. Onodera for helpful discussions and the technical assistance. This work was supported by the Core Research for Evolutional Science and Technology (JPMJCR15F3), Japan Science and Technology Agency (JST).
Author information
Authors and Affiliations
Contributions
S.M. conceived the data analysis scheme, implemented the software, analyzed optical microscope images, and wrote the manuscript. T.M. supervised the research program.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Masubuchi, S., Machida, T. Classifying optical microscope images of exfoliated graphene flakes by data-driven machine learning. npj 2D Mater Appl 3, 4 (2019). https://doi.org/10.1038/s41699-018-0084-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41699-018-0084-0
This article is cited by
-
Van der Waals enabled formation and integration of ultrathin high-κ dielectrics on 2D semiconductors
npj 2D Materials and Applications (2024)
-
Physically informed machine-learning algorithms for the identification of two-dimensional atomic crystals
Scientific Reports (2023)
-
Automatic detection of multilayer hexagonal boron nitride in optical images using deep learning-based computer vision
Scientific Reports (2023)
-
Review: 2D material property characterizations by machine-learning-assisted microscopies
Applied Physics A (2023)
-
Universal image segmentation for optical identification of 2D materials
Scientific Reports (2021)