Prediction of a room-temperature eight-coordinate two-dimensional topological insulator: penta-RuS₄ monolayer

Abstract

We predict a stable eight-coordinate two-dimensional RuS₄ monolayer, with a trilayer S–Ru–S and pentagonal rings tiling configuration by first-principles calculations. This monolayer exhibits unique anisotropic quadratic energy dispersion with two Dirac points emerging at the high-symmetric Γ point. When the spin-orbit coupling is included, a large nontrivial energy gap (70 meV) appears near the Fermi level. The topological nature of RuS₄ monolayer is also confirmed by the nontrivial Z₂ invariant and gapless edge states. A four-band tight-binding model is further proposed, which reveals that the topological states arise from the indirect interaction of the Ru-d _xz and d _yz orbitals.

Introduction

The discovery of topological insulators (TIs) has sparked enormous efforts in the search for materials with similar electronic structures, because of their rich physics and promising applications in quantum devices and spintronics.^1,2,3 TIs are materials with bulk energy gap but gapless surface or edge states. Because of protection by time-reversal symmetry, the helical edge states in two-dimensional (2D) TIs are spin locked and robust against perturbation, known as quantum spin Hall (QSH) effect, which may lead to low-power-consumption electronic devices. So far, several 2D TIs have been predicted theoretically, such as elementary substances (graphene, graphynes, silicene, germanene, stanene, bismuthene),^4,5,6,7,8,9 binary compounds (PbTe, SnSe₂, hexagonal WS₂, 1 T′-WTe₂),^10,11,12,13 heterostructures (graphene/BiTeI, VO₂/TiO₂),^{14, 15} and organometallic compounds.^{16, 17} However, the experimental observation of 2D TIs remains challenging. This is not only because of ultralow temperature, such as HgTe/CdTe and InAs/GaSb quantum wells with small SOC band gaps,^{18, 19} but also due to the influence of substrates, such as silicene on Ag(111) surface,²⁰ and germanene on 2H-MoS₂.²¹ Therefore, the search for new 2D TIs with large SOC gaps and high stability has become critically important.

Currently, most reported 2D materials are square or hexagonal lattices. Pentagonal ring-based 2D crystals, another new configuration of 2D materials, have also been predicted computationally and they can be roughly divided into two poly-types in light of the sort of the center atom: one is group IV element based compounds, such as pentagonal graphene,²² CB₂,²³ SiX (X = B, C, and N),²⁴ and SnX₂ (X = S, Se, and Te);¹¹ the other is four-coordinate noble metal compounds, such as PdS₂ ²⁵ and PdSe₂.²⁶ In this work, based on chemical intuition, we design an eight-coordinate pentagonal 2D compound, RuS₄ monolayer. To the best of our knowledge, the 2D material with eight-coordinate configuration is never reported yet. More notably, this predicted RuS₄ monolayer also exhibits anisotropic quadratic energy dispersion near the Fermi level, and a rare multi-merging of two Dirac points with the 2π Berry phases. In addition, when the spin-orbit coupling (SOC) is included, a nontrivial topology emerges in its electronic structure, with a SOC gap of 70 meV, suggesting it is a promising 2D room-temperature QSH insulator.

Results and discussion

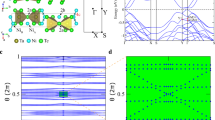
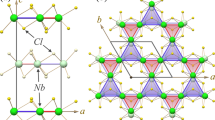
The schematic structures of RuS₄ monolayer are shown in Fig. 1a, b. The symmetry space group of RuS₄ monolayer is P4/mbm. The optimized lattice parameters are a = b = 5.318 Å. The square primitive cell contains two Ru and eight S atoms. Each Ru atom is coordinate with eight S atoms, and each S atom binds to two Ru atoms and one S atom, forming a beautiful pentagonal ring network known as the Cairo pentagonal tiling.²⁷ The S–S bond length is 2.096 Å, and the 2D projected length of Ru–S bond length (2.516 Å) is 2.056 Å, so the Ru–S penta-rings are close to equilateral pentagons in the top view. From the side view, we can see a triple-layer structure with a Ru layer sandwiched by two S layers. Moreover, we find the eight-coordinate Ru atoms sitting in the center of the square prism of S atoms, as shown in Fig. 1c. The height of the prism of 2.900 Å (h in Fig. 1c), is close to the side length of 2.908 Å (d in Fig. 1c), suggesting the Ru atoms are in the D _4h crystal field. Figure 1d shows the first Brillouin zone of RuS₄ monolayer, which is also square with four X points on the side centers and four S points on the corners.

Fig. 1

Top view a and side view b of optimized RuS₄ monolayer. The dashed rectangle refers to the unit cell. c Schematic configuration of eight-coordinate Ru atom in monolayer RuS₄. d 2D Brillouin zones of monolayer RuS₄ with high-symmetry points labeled. e Phonon dispersion of RuS₄ monolayer

To assess the stability of RuS₄ monolayer, we calculated the phonon dispersion curves. The absence of any imaginary frequency confirms that this structure is at least a local minimum in its energy landscape (Fig. 1e). The cohesive energy (E _c) is calculated according to the formula, ${E_c} = 2{E_{Ru}} + 8{E_S} - {E_{Ru{S_4}}}$, where ${E_{Ru{S_4}}}$ is the total energy of the RuS₄ monolayer unit cell (with 2 Ru atoms and 8 S atoms), E _S and E _Ru are the energies of the single S and Ru atom in vacuum, respectively. The calculated E _c is 40.4 eV per unit cell or 4.04 eV per atom, implying that the 2D penta-RuS₄ sheet could be synthesized for energetic preference. Note that the bulk RuS₂ in cubic pyrite structure is the only reported compound in the Ru–S phase diagram,²⁸ which owns a larger E _c (5.16 eV per atom). It is not surprising as ultrathin 2D materials are often metastable structures. In fact, the very recently synthesized 2D boron sheets own much less E _c than its bulk form.^29,30,31 For these types of ultrathin metastable materials, molecular beam epitaxy may be the best choice, which has successfully been used to fabricate silicene,²⁰ germanene,²¹ and stanene.³² Moreover, as each of Ru atoms is saturated by eight S atoms in penta-RuS₄ monolayer, this material should not be easily oxidized, i.e., it can be used without a high vacuum condition or protective capping materials, which distinguishes it from other 2D materials such as silicene and germanene.^{20, 21}

The electronic properties of fully relaxed RuS₄ monolayer are presented in Fig. 2a. The valence band (VB) and the conduction band (CB) touch together at the high-symmetric Γ point in the Brillouin zone, with the Fermi level (E_F) locating exactly at the crossing point. When the spin degree of freedom is taken into account, the energy dispersion is the four-fold degenerate crossing at the Γ point. The projected density of states (PDOS) shows that the states near the E_F are contributed by the hybridization of Ru-d and S-p orbitals. The 3D landscape of valence and conduction bands is also depicted in Fig. 2b, which clearly presents the anisotropic dispersion with square symmetry.

Fig. 2

a Electronic band structures and PDOS of RuS₄ monolayer without SOC. b 3D landscapes of the highest valence band (VB) and the lowest conduction band (CB) around Γ point, and the right panel shows the energy contour of the difference between VB and CB with an energy contour interval of 0.01 eV

As Ru is a heavy atom, we further consider the SOC effect in the band structure calculations by performing fully non-collinear magnetic structure computations after obtaining the nonmagnetic ground state of the system. As shown in Fig. 3a, b, the RuS₄ monolayer exhibits a direct band gap as large as 70 meV, which is observably above the energy scale of room temperature. The remarkable SOC-induced gap is also shown in Fig. 3c, with the approximate planar roof and floor of VB and CB, respectively. This suggests RuS₄ monolayer may be a topological insulator. To verify the topological nature of the insulating phases of RuS₄ monolayer, following the method developed by Fu and Kane,³³ the Z₂ topological invariant is calculated by the product of parity eigenvalues for all the occupied bands at the four time-reversal invariant points in the 2D Brillouin zone, (Supplementary Table. S1) as the structure possesses space inversion symmetry. The Z₂ index ν = −1 demonstrates that the RuS₄ monolayer is, indeed, a 2D TI. We also perform calculations to examine the topological edge states on the RuS₄ nanoribbon, since it is the direct evidence of the 2D TI and QSH states. By using the WANNIER90 package,³⁴ we fit a tight-binding (TB) Hamiltonian with maximally localized Wannier functions to the bands calculated by the first-principles method with SOC (Supplementary Fig. S1). Then we build a 1D model structure of the RuS₄ nanoribbon with symmetric edges and 30 units (Fig. 3d). The band structure of RuS₄ nanoribbon is obtained by a direct diagonalization of the TB Hamiltonian of the ribbon along the 1D Brillouin zone. The edge states apparently disperse in the 2D band gap and cross the E_F at the Γ point, as presented in Fig. 3e. The feature of gapless edge states explicitly demonstrates the nontrivial nature of 2D RuS₄ material.

Fig. 3

a Energy band structure of RuS₄ monolayer with SOC. b Magnified plot of electronic band structure along the X–Γ direction, with VB, CB, and SOC-induced gap labeled. c 3D landscapes of VB and CB with SOC. d Schematic representation of the supercell used to model the open boundary conditions. Shaded regions are used to illustrate the edge cells. e Electronic band structures of RuS₄ [30 × 1 × 1] nanoribbon. The helical edge states are denoted by the red circles

In the band structure of RuS₄ monolayer without SOC, the VB and CB cross at the Γ point and exhibit a quadratic dispersion relation in both Γ − X and Γ − S directions, which is quite different from the linearly cross point in the single Dirac cone 2D materials, such as graphene and silicene.^{6, 7} Furthermore, the anisotropic quadratic dispersion of the RuS₄ monolayer also differs from the semi-Dirac cone 2D materials with two or three Dirac points merging (such as 6,6,12-graphyne,⁵ and TiO₂/VO₂ multilayer¹⁵), which show the linear energy dispersion in one principal axis and quadratic in the other.³⁵ When a uniaxial strain is applied, the band structure of the RuS₄ monolayer retains gapless, and the two Dirac cones emerge along the kx-axis (Γ − X direction) or ky-axis (Γ − X′ direction) depending on the direction of the uniaxial strain (Fig. 4a, b). When the uniaxial strain increases, the two Dirac cones are separated and move farther away from each other (Supplementary Fig. S2a). The unique quadratic energy dispersion can be viewed as the consequence of the merging of two conventional Dirac points with the same Berry phase at the high-symmetric Γ point. Furthermore, the degenerate parabolic band contact point can be separated into two linear Dirac cones under distortion strain (Supplementary Fig. S2b). It can also be split into two spin-subband contact points under a magnetic field (Supplementary Fig. S2c, d). The phonon dispersions for RuS₄ monolayer under equibiaxial strains are calculated by Density Functional Perturbation Theory (DFPT) model, which indicates RuS₄ monolayer can withstand a strain from −2 to +1% (Supplementary Fig. S3). These indicate that the merging Dirac point in the RuS₄ monolayer is rather robust and topologically stable under an external perturbation and magnetic field, in contrast to the merging of two Dirac points with opposite Berry phases in the semi-Dirac cone case.³⁶

Fig. 4

a, b 3D landscapes of VB and CB structures of RuS₄ monolayer without SOC under the uniaxial tensile strain in two perpendicular directions

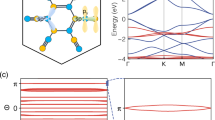
To get a better understanding of the origin of the nontrivial band topological gap, we present the schematic diagram of the Ru-d _xz, d _yz band and S-p _z bands evolution at the Γ point under the crystal field and the SOC effect in Fig. 5a. Under the D _4h symmetry of the crystal group, five d orbitals of Ru atoms split into three single d _z ², d _xy and d _x ² − _y ² orbitals and a doubly degenerate d _xz, d _yz orbitals. Because there are two kinds of S dimers in unit cell, the top S dimer and bottom S dimer, the four S-p _z orbitals of two S dimers form the two bonding states and two antibonding states, as schematically illustrated in Fig. 5a. The band inversion occurs between the $\left| {p_z^ + } \right\rangle$ state and the $\left| {p_z^ - } \right\rangle$ state, where the superscripts +(−) represent the even (odd) parity of the corresponding states, respectively. It is a nontrivial band order that caused by the crystal field. According to the partial band projections in Fig. 5b, the electronic states around the E_F are mainly contributed to the Ru − d _xz, d _yz orbitals and S-p _z orbitals, so the other orbitals can be reasonably neglected in the following discussion. The d _xz, d _yz-orbitals also split into bonding and antibonding states due to the formation of chemical bonding between Ru and S atoms. These states can be labeled as $\left| {d_{xz \pm iyz}^ + } \right\rangle$ and $\left| {d_{xz \pm iyz}^ - } \right\rangle$. Without SOC, the $\left| {d_{xz \pm iyz}^ + } \right\rangle$ and $\left| {d_{xz \pm iyz}^ - } \right\rangle$ states are degenerate at the Fermi level, rendering the system a semimetal. When including SOC, the $\left| {d_{xz \pm iyz}^ + } \right\rangle$ state splits into two doubly degenerate states, i.e., $\left| {d_{xz + iyz, \uparrow }^ + d_{xz - iyz, \downarrow }^ + } \right\rangle$ and $\left| {d_{xz - iyz, \uparrow }^ + d_{xz + iyz, \downarrow }^ + } \right\rangle$, accordingly, a nontrivial gap is opened. The symbols $\left| \uparrow \right\rangle$ and $\left| \downarrow \right\rangle$ do not represent real spin states for SOC, but denote two states of Kramer doublets. Obviously, the SOC-induced band exchange does not change the nontrivial band topology, for the $\left| {d_{xz + iyz, \uparrow }^ + d_{xz - iyz, \downarrow }^ + } \right\rangle$ and $\left| {d_{xz - iyz, \uparrow }^ + d_{xz + iyz, \downarrow }^ + } \right\rangle$ states with the same parity. Note that 2D TIs, such as SnF⁸ and β-SnSe₂,¹¹ also exhibit a quadratic dispersion at Γ point in the band structure without SOC. However, the type of SOC-induced band exchange is different. There is the s-p-type band inversion in SnF, and the p _z-p _xy-type band inversion in β-SnSe₂. For this reason, the band gap is indirect in the band structure with SOC in SnF and β-SnSe₂. On the contrary, a direct SOC band gap appears in RuS₄ monolayer between the Ru-d _xz,_yz bands with the same type d orbitals, with the band inversion occuring between the $\left| {S - p_z^ + } \right\rangle$ state and the $\left| {S - p_z^ - } \right\rangle$ state.

Fig. 5

a Schematic diagram of the band evolution of 2D RuS₄ at the Γ point under the crystal field effect and SOC. The Fermi level is indicated by red dash line and the superscripts + and − represent the bonding and antibonding states, respectively. b The Ru-d _xz,yz and S-p _z orbital projected character of bands with SOC. The symbols + and − label the parities of the bands at the Γ point

In the pentagonal RuS₄ crystal lattice, there are two non-equivalent sites of Ru atoms, as shown in Fig. 6a, b. There are two kinds of the virtual nearest-neighbor hopping paths between the A site and B site within the unit cell. One path is through the single S atom, another is through the S-S dimer, labeled as t ₁ and t ₂, respectively. In contrast, there is only one path connecting the next nearest-neighbor sites between the sites of adjacent cells, and this coupling is also through the S–S dimer (Fig. 6a). Besides these, there is on-site hopping parameter t₃ due to the Ru atoms sandwiched by two S layers (Fig. 6b). Based on the orbital occupancy analysis above, we only focus on the low-energy states from d _xz, d _yz orbitals. Therefore, a four-band low energy effective Hamiltonian with SOC around the Γ point can be described by

$$\\ {H_{eff}} = - ( {{t_1} + {t_2}} ){k_x}{k_y}{\sigma _x} \otimes {I_{2x2}} - {t_2}({k_x^2 - k_y^2} ){\sigma _z} \otimes {I_{2x2}} \\ - {t_3}( {k_x^2 + k_y^2} ){I_{4x4}} + {\lambda _{SO}}\left( {1 - k_x^2{\rm{/}}8 - k_y^2{\rm{/}}8} \right){\sigma _y} \otimes {s_z},\\ \\ $$

(1)

where the Pauli matrix σ indicates the $\left| {d_{xz + iyz}^ + } \right\rangle$ and $\left| {d_{xz - iyz}^ + } \right\rangle$ orbital degrees of freedom, s is the Pauli matrix of spin, ${I_{2x2}}$(${I_{4x4}}$) is the 2 × 2 (4 × 4) identity matrix, t ₁, t ₂, and t ₃ are related to band parameters, and λ _SO is effective SOC. The above equation results in an energy spectrum $( {\vec k} ) = - {t_3}( {k_x^2} + {k_y^2} ) \pm \sqrt {{{[{( {{t_1} + {t_2}} ){k_x}{k_y}} ]}^2} + t_2^2{{( {k_x^2 - k_y^2} )}^2} + \lambda _{SO}^2{{( {1 - k_x^2{\rm{/}}8 - k_y^2{\rm{/}}8} )}^2}}$ with a gap E _gap  = 2λ _SO at the Γ point. The comparison between the effective Hamiltonian and the density-functional theory (DFT) band structures is presented in Fig. 6c, d for without and with SOC effect, respectively. The corresponding fitting parameters are t ₁ = 520 eV, t ₂ = 280 eV, t ₃ = 60 eV, and λ _SO  = 0.035 eV. This four-band TB model well reproduces the DFT band structure in low energy range nearby the Γ point. We note that the fitting parameter t₁ is 1.86 times as large as the value of t₂, indicating the coupling strength of the d _xz, d _yz orbitals through a single S atom is about twice that of the S–S dimer. The non-zero fitting parameter t₃ in our model suggests the on-site energy correction cannot be ignored, although it is much smaller than t₁ and t₂. When the spin-orbit coupling is vanishing, Hamiltonian (1) has a touching point between the conduction and valence bands at the Γ point and the dispersion relation near the touching point is quadratic, which is in line with above first-principle calculations. The quadratic touching point can be considered as a double Dirac point that is formed by merging two Dirac points with the same topological charge, implying that the conduction and valence bands have the same parity at Γ point. Therefore, the band inversion does not induce a topological phase transition between a quantum spin Hall insulator and a trivial band insulator. Clearly, our model is in stark contrast to the typical models supporting the existence of quantum spin Hall effect, e.g., the Bernvig–Hughes–Zhang Hamiltonian,¹⁸ which has two Dirac points with the opposite topological charges when the spin-orbit coupling is absent. Furthermore, in the Bernvig–Hughes–Zhang Hamiltonian, the conduction and valence bands have opposite parities and the band inversion induces a topological phase transition.

Fig. 6

a, b The unit cell of penta-RuS₄ monolayer containing two nonequivalent Ru atoms, marked by site A and B. The dashed lines materialize the virtual hopping between different sites designated as t ₁, t ₂, and the on-site hopping designated as t ₃. The comparison between DFT and TB calculated band structures c without SOC and d with SOC around the Γ point

We further investigate the strain effect and external magnetic field effect on the merging point of two Dirac points. When the strain and external magnetic field induced perturbations (H _pert ) to the lowest order are simultaneously considered, the TB Hamiltonians take the form of

$$\\ {H_{eff}} + {H_{pert}} = - ( {{t_1} + \sqrt {{t_x}{t_y}} } ){k_x}{k_y}{\sigma _x} \otimes {I_{2x2}} \!-\! ( {{t_x}k_x^2 \!-\! {t_y}k_y^2 \!+\! \Delta }){\sigma _z} \otimes {I_{2x2}} \\ - {t_3}({k_x^2 + k_y^2} ){I_{4x4}} + {\lambda _{SO}}({1 - k_x^2{/}8 - k_y^2{/}8} ){\sigma _y} \otimes {s_z} + m{I_{2x2}} \otimes {s_z},$$

(2)

where t _x and t _y are the corresponding hopping parameters in different directions (assuming t _x  > 0 and t _y  > 0 without loss of generality), the parameter ${\rm{\Delta }} = 2( {{t_x} - {t_y}} )$ and m are chosen to mimics a strain and external field, respectively. Apparently, applying an uniaxial strain along the x or y axis would change the relative values of t _x and t _y , and therefore Δ is nonzero. In the absence of SOC and external magnetic field, when Δ > 0, there are two Dirac cones locating at $k = ( {0, \pm \sqrt {\Delta {/}{t_y}} } )$, while there are two Dirac cones locating at $k = ( { \pm \sqrt { - \Delta {\rm{/}}{t_x}} ,0} )$ when Δ < 0, in good agreement with above first-principles calculation results (Fig. 4a, b). In the presence of a magnetic field (m ≠ 0) and no strain (Δ = 0), there always exists twofold energy degenerate points at the Γ point (Supplementary Fig. S2c). The SOC-gap is robust against weak magnetic field corresponding to $m{\rm{/}}{\lambda _{SO}} < 1$. When $m{\rm{/}}{\lambda _{SO}} >1$ the two spin subbands will cross over with each other, resulting in the SOC-gap vanishing.

In summary, we design an eight-coordinate 2D penta-RuS₄ monolayer, which is demonstrated to be energetically and dynamically stable within the framework of DFT calculations. The penta-RuS₄ monolayer exhibits the unique anisotropic parabolic band contact point near the Fermi level, derived from the merged two Dirac points with the same Berry phase at the high-symmetric Γ point. More interestingly, the penta-RuS₄ monolayer is found to be a robust 2D TI and the strong SOC opens the nontrivial bandgap as large as 70 meV. The four-band TB model is proposed and reveals that the nontrivial topological states originate from the indirect interaction of d _xz and d _yz orbitals of Ru atoms. The unique eight-coordinate pentagonal structure, high stability, two Dirac cones merging near the Fermi level and large nontrivial band gap make the penta-RuS₄ monolayer have fundamental research interest and hold potential applications in the room temperature QSH devices.

Methods

DFT calculation

All first-principles computations are carried out using the Vienna ab initio simulation package (VASP)^{37, 38} based on theDFT, with the projector augmented wave and Perdew–Burke–Ernzerhof exchange–correlation functional.³⁹ The plane-wave cutoff is set to be 500 eV, and the Monkhorst–Pack scheme⁴⁰ of a 9 × 9 × 1 k-point mesh is applied for geometry optimization, while a denser grid (13 × 13 × 1) is used for electronic structure calculation. The 2D system is separated from its periodic image by a vacuum distance of 15 Å in the perpendicular direction. All structures, including the lattice parameters and the internal ion coordinates, are fully optimized with a residual force tolerance of 0.001 eV/Å. Phonon dispersion calculations are performed by using the DFPT method as implemented in the VASP combined with the Phonopy code.⁴¹

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.