Abstract
Mountain glacier systems are decreasing in volume worldwide yet relatively little is known about their upper reaches (>5000 m). Here we show, based on the world’s highest ice core and highest automatic weather stations, the significant and increasing role that melting and sublimation have on the mass loss of even Mt. Everest’s highest glacier (South Col Glacier, 8020 m). Estimated contemporary thinning rates approaching ~2 m a−1 water equivalent (w.e.) indicate several decades of accumulation may be lost on an annual basis now that glacier ice has been exposed. These results identify extreme sensitivity to glacier surface type for high altitude Himalayan ice masses and forewarn of rapidly emerging impacts as Mt. Everest’s highest glacier appears destined for rapid retreat.
Similar content being viewed by others
Introduction
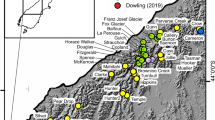
The worldwide retreat of mountain glaciers in recent decades is well documented1 and the resulting loss of water storage capacity for agriculture, hydropower, and both human and ecosystem consumption have significant impacts on the 250 million people living near mountain glaciers2. In addition, more than 1.6 billion people are recipients of water from mountain regions and 50% of Earth’s biodiversity centers are in mountain regions2. However, the upper reaches (>5000 masl) of mountain landscapes have received relatively little scientific attention leaving gaps in knowledge concerning the key drivers influencing atmospheric circulation, changes in snow and ice extent over time, and climate model verification that together will decrease uncertainty in the climate change projections needed to plan a sustainable future3. Within the Hindu Kush Himalaya (HKH) lie Earth’s highest mountains including the foremost Mt. Everest (Sagarmatha, Qomolangma, 8848.86 m). Despite its iconic status and having been climbed >7000 times, Mt. Everest remains in its highest reaches poorly understood in terms of weather, climate, and glacier health. To fill some of these knowledge gaps National Geographic and Rolex’s Perpetual Planet Everest Expedition mounted in April/May 2019 the most comprehensive scientific investigation of the Nepalese side of Mt. Everest thus far undertaken, including studies in biology, geology, glaciology, meteorology, and mapping4. This expedition resulted in (Fig. 1): the world’s highest ice core - recovered from Mt. Everest’s highest glacier (27.977211, 86.929861; 8020 m, South Col Glacier (SCG), mean annual air temperature 1991–2020 = −22.6 °C); and the world’s two highest automatic weather stations (AWSs) located along the southern climbing route of Mt. Everest at 7945 m on South Col and 8430 m on the Balcony5. In the following, we investigate the timing and cause of the significant SCG mass loss documented during our investigation and the implications for high mountain glacier systems.
Results
Estimated SCG thickness decrease and timing
Moraines surrounding SCG attest to the past larger extent of the glacier (Supplementary Fig. 1) assumed to mark its Little Ice Age position (1300s to late 1800s6). Except for seasonal snow and a perennial snow/firn apron on the flanks of Mt. Everest, which form the upper reaches of this southerly facing glacier, SCG’s surface is primarily exposed ice. Logistic constraints (oxygen and weather) restricted the time available to drill and package the ice core to two hours resulting in a surface to 10 m depth retrieval of ice (average density ~0.89 gm/cm3) from what is estimated to be its current ~30–50 m thickness. Aerosol-based micro-radiocarbon7 dating of the upper 10–69 cm of the SCG ice core reveals an age of 1966 ± 179 years ago. Identification of annual layers in the SCG ice core, using ultra-high resolution (153 μ) sampling8,9 of magnesium (winter/spring maxima), as previously demonstrated for the East Rongbuk Glacier ice core10 (ERG; 6518 m, ~5 km north of SCG), reveals a net annual layer thickness of ~27 mm w.e. a−1 for the SCG ice core (Supplementary Fig. 2). If we assume this is representative of the last 2000 years, multiplying by the near-surface age this yields an estimated net thinning of SCG of ~55 m w.e. ERG ice core annual layer counted dating reveals an age of ~500 years ago at ~80 m w.e. depth11 and a model estimated depth of ~2000 years ago at 108 m suggesting ~50% less ice thickness for the same age at SCG. In addition, estimated modern precipitation for SCG (Methods section) is ~50% of the ~480 mm w.e. a−1 derived for ERG modern precipitation11. While a definitive ice thickness loss cannot be determined we suggest that by comparison with the ERG ice core our SCG ice thinning estimate is reasonable.
To determine the timing of the ice loss on SCG we refer to written records, photogrammetry, ice core and meteorological records, and climate reanalysis for the region. A synthesis of written and photographic records of retreat/advance states of 112 Himalayan glaciers covering the period 1812–1965 demonstrate that some glacier recession started as early as 1860, but with considerable temporal and spatial variability12. More recent syntheses suggest that glacier mass loss has been the overall trend since the 1950s with the greatest rate of glacier area loss since ~200013. For the south side of Mt. Everest, combined photogrammetric and satellite imagery reveals thinning greater than 100 m up to 5700 m since 1962, with a near doubling in rate since 200914. Climate reanalysis data show June/September freezing level heights rising ~7 m per year since 200515 and an AWS operated May/July 2005 near the ERG ice core site reveals the increased ablation effect of cloud cover16. Ice cores collected in 1980 show the effects of melting at 6100 and 6400 m on the Khumbu Glacier17. Air content used as a proxy for summer temperature measured in the ERG ice core indicates that the last ~100 years have been the warmest in the last 2000 years18.
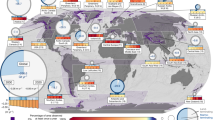
While SCG is at a significantly higher elevation than sites previously noted we suggest that its thinning (~55 m w.e.) likely follows the overall ice mass loss trajectory in the region by starting in the mid-late 1800s, increasing as of the 1950s, and most marked since ~2000. The newly extended fifth major global reanalysis of the European Centre for Medium-Range Weather Forecasts (ERA5) that extends back to 195019 suggests large-scale warming of annual surface temperature over Asia starting in the late 1990s (Supplementary Fig. 3) with the most significant warming over the Tibetan Plateau and northern slope of the Himalayas for the period 2001–2020 minus 1979–2000 approaching ~2 °C in winter and a smaller increase in summer (Fig. 2). ERA5 reanalysis focused over Mt. Everest reveals a sharp demarcation of warming below 150 hPa as of the late 1950s with the most intense warming starting in the late 1990s (Fig. 3 and Supplementary Fig. 4).
Annual 2-meter temperature anomaly maps for a December–February (DJF) and b July–August (JJA). The anomaly values are for the period 2001–2020 minus 1951–2000 climatology. The location of Mt. Everest is circled and labeled “EV”. Data from the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA-5 reanalysis (ERA5)19. Maps generated using Climate Reanalyzer33.
Time/height profiles over Mt. Everest for temperature (2 m). The dashed line indicates the approximate level of Mt. Everest summit. Annual anomalies are relative to 1951–2000 climatology. Data from the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA-5 reanalysis (ERA5)19. The dashed line indicates the approximate level of Mt. Everest summit. Annual anomalies are relative to 1951–2000 climatology. Supplementary Figure 4 reveals the similarity in results between ECMWF ERA-5 and NOAA Twentieth Century Reanalysis Version 3 demonstrating that the inclusion of satellite data in the ERA 5 reanalysis does not impact the interpretation developed in this paper. Generated using Climate Reanalyzer33.
Modeling SCG snow and ice loss
To explore whether recent meteorological trends can be reconciled with SCG ice loss we perform experiments using the COSIPY model (COupled Snowpack and Ice surface energy and MAss balance model)20 applied to downscaled ERA5 data (Fig. 4; Methods section). First, we assess the extent to which changes in climate (Supplementary Fig. 5; air temperature, relative humidity, wind speed, and precipitation, short- and longwave radiation) explain the glacier mass loss. We do so by simulating the energy and mass fluxes for a prescribed snowpack (1950–2019; Methods section), assumed to be in surface mass balance (SMB) for the first decade of the experiment (1950–1959). During this period of equilibrium, we find sublimation to be by far the main process of mass loss (mean loss = 77 mm w.e. a−1), over 35 times the (minimal) surface melt (2 mm w.e. a−1), in agreement with energy balance simulations from relatively high altitude, low-latitude glaciers elsewhere21,22. We find no significant trend in snowfall over the full simulation period (1950–2019), but upward in sublimation of 0.22 [95% confidence interval: 0.10–0.38] mm w.e. a−2. Whilst surface melt remains negligible throughout the snow simulation, it does exhibit a significant upward trend of 0.04 [0.01–0.07] mm w.e. a−2, and it combines with the uptick in sublimation to drive a significant decline in the SMB of −0.33 [−0.51 to −0.14] mm w.e. a−2 (Supplementary Fig. 6). Both physical and empirical lines of evidence (Methods: Sublimation & Melt Sensitivity to Climate Forcing) identify the increasing air temperature as playing a key role in explaining the sublimation trend. As the surface warms, saturation vapor pressure grows at the Clausius Clapeyron rate, generating an ever-greater moisture gradient from the surface into the atmosphere for fixed relative humidity. At the SCG declining relative humidity amplifies this gradient further, with strengthening winds also helping to increase sublimation by enhancing turbulent heat exchange. This experiment demonstrates that even if SCG snowpack was in SMB in the middle of the 20th century, changing climate likely drove considerable thinning since then, with a cumulative SMB of −1530 mm w.e. by the end of 2019.
Annual means for meteorological variables downscaled to SCG. See Methods section for details of the downscaling. Panel a: Ta is air temperature (Ta) panel b is relative humidity (γ), panel c is wind speed (U), panel d is precipitation (PPT), panel e is incident shortwave radiation (SW), and panel f is incident longwave radiation (LW).
A second COSIPY experiment involved running with no initial snowpack, enabling estimation of the potential rate of mass loss once ice is exposed at SCG. The results indicate a mean 1950–2019 SMB of −1929 mm w.e. a−1, with a significant downward trend of −3.7 [−5.9 to −1.5] mm w.e. a−2. Mean annual ablation (the sum of sublimation and melt) is over 20 times greater in the ice simulation (1964 mm w.e. a−1) compared to the snow simulation (96 mm w.e. a−1), due to sublimation increasing by a factor of 4.9 (from 93 to 456 mm w.e. a−1) and the initiation of widespread melting as a tipping point is crossed, rising from negligible amounts when the SCG was snow covered (3.3 mm w.e. a−1) to significant meltwater generation for the ice surface (1508 mm w.e. a−1). Once the snowpack is replaced by ice that reflects less than half the insolation, the SCG surface is more often raised to 0 °C. After being warmed to the melting point, additional energy gains from solar heating are less easily lost to the turbulent and longwave fluxes (which would otherwise amplify as the glacier surface warms relative to the atmosphere). Energy must therefore be dissipated through melting once the glacier surface reaches 0 °C, much like the spillway that diverts runoff once a reservoir has filled (Supplementary Fig. 10). The high receipts of insolation at the South Col5 help explain this acute sensitivity of the surface energy balance to surface reflectivity, consistent with other low-latitude glaciers at relatively high elevation23,24,25.
The COSIPY experiments therefore outline a plausible mechanism for dramatic mass loss at SCG. First, once glacier ice is regularly exposed, the results suggest that the ~55 m w.e. thinning could occur in ~25 years, over 80 times faster than the ~2000 years it took to form the ice now exposed at the surface of SCG. Second, the COSIPY snow simulation indicates that the transition from a permanent snow/firn surface to majority ice-cover could have been triggered by climate change since 1950, with sublimation enhanced by rising air temperatures playing the critical role. Although the total mass of snow lost at the SCG is unknown and would be sensitive to the onset of negative mass balances (which could pre-date 1950)12, and the physical properties of the snowpack (e.g., its temperature and capacity for refreezing of meltwater)20, the modeled thinning provides a plausible mechanism to expose glacier ice. We also note that whilst the magnitude of the snow loss is sensitive to parameter uncertainty in our simulations, the interpretation of thinning is not (Supplementary Information). Similarly, whilst the ability of ERA5 to capture historic climate variability for the high Himalaya is unknown, warming of the upper troposphere is a robust and widespread feature of anthropogenic climate change26 and physical considerations of the surface energy balance identify that enhanced sublimation should follow from this heating (Methods section). We therefore highlight that the increasing ablation of snowpack identified here is, in the absence of other changes in meteorology, the expected response to greenhouse gas forcing. The surface mass balance in the ice simulations is also impacted by parameter uncertainty, but our interpretation of rapid loss (at least 1200 mm w.e. a−1) is robust across all scenarios considered.
Discussion
Beyond illustrating that climate change may have driven dramatic mass loss at SCG in recent decades, our simulations also highlight mechanisms that may be of much broader significance for glacier retreat across the Himalaya. First, we find that the region’s extreme insolation means that ablation can accelerate by over a factor of 20 as snow cover gives way to glacier ice. This is particularly critical for glaciers like SCG that have relatively small snow accumulation rates. Second, climate trends have led to mainly sublimation-driven thinning of high-altitude snowpack since 1950, making such transitions more likely. This mechanism is significant because our results indicate that whilst warming air temperatures did the most to enhance sublimation, declining relative humidity and strengthening winds also played a role, which should have acted to suppress melting (Methods section). This contrasting behavior underlines the theoretical shortcoming of widely used empirical glacier ablation models27 and highlights the need to differentiate between these processes when projecting future glacier mass balance. The latter is essential to anticipate the type of highly non-linear mass loss identified here. In identifying sublimation as a major control on the mass balance, our results add to the consensus regarding the high sensitivity of low-latitude ice masses to moisture variability28. We also note that the acceleration of upper-atmosphere winds we report may have enhanced snow ablation at the SCG by increasing physical deflation, a process not considered in our simulations, yet also capable of triggering rapid glacier loss if it leads to more frequent ice exposure.
Warming will also change the experience associated with Mt. Everest ascents as loss of high elevation snow and ice cover continues to thin exposing bedrock; warm thicker air increases oxygen availability29; ice block movement in the Khumbu icefall and avalanches becomes even more dynamic; and glacier melt destabilizes the Khumbu base camp that is home to ~1000 climbers and logistics teams during the climbing season.
Climate predictions for the Himalaya all suggest continued warming and continued glacier mass loss13. We find the transition from snow covered to exposed ice can change the state of the glacier from one of equilibrium to one of extremely rapid mass loss. At an estimated thinning rate approaching 2000 mm a−1 even glaciers such as SCG that are above 8000 m may disappear by mid-century. Our study points to the critical balance afforded by snow-covered surfaces and the potential for loss throughout high mountain glacier systems as snow cover is depleted by changes in sublimation and surface melt driven by climate trends. Everest’s highest glacier has served as a sentinel for this delicate balance and has demonstrated that even the roof of the Earth is impacted by anthropogenic source warming.
Methods
Meteorology
We reconstruct the meteorology at the South Col using observations from the automatic weather station (AWS) there (at 7945 m a.s.l)5 to downscale ERA5 reanalysis via a parsimonious blend of bias correction and machine learning. Initial screening indicates strong correlations between hourly ERA5 pressure level data bilinearly interpolated to South Col and air temperatures (r = 0.98), wind speed (r = 0.94), and relative humidity (r = 0.80) observed by the AWS. We therefore apply a simple empirical quantile mapping correction29 to remove systematic bias for these variables.
Incident shortwave (SW) and longwave (LW) radiation are not available on ERA5 pressure levels, so we reconstruct them by downscaling the transmissivity (τ) and emissivity (α) of the atmosphere, defined:
Where Ψ is the theoretical top of atmosphere solar radiation, σ is the Stefan Boltzmann constant (5.67 × 10−8 W m−2 K−4), and Ta is the 2 m air temperature (Kelvin). Observed values for τ and α are evaluated using AWS measurements of incident radiation and air temperature (using calculations of solar geometry to compute Ψ). We then train a Random Forest model (with 100 trees and a minimum leaf size of three) using Python’s Scikit Learn (version 0.20.1), modeling τ and α as a function of the ERA5 predictors in Methods Table 1. SW and LW could then be computed from:
Where T is the estimate from the bias-corrected ERA5 data.
We calibrate the bias correction and RF models using between 5012 (wind speed) and 12,810 (air temperature) overlapping hours of AWS observations and ERA5 data (May 2019 to December 2020). We evaluate the performance using a fivefold cross-validation, with results indicating very strong agreement between the observed and downscaled meteorology: hourly Pearson correlations range from 0.83 (relative humidity) to 0.98 (air temperature), translating respectively to root mean square errors between ~31 and 8% of the observed means (Supplementary Fig. 7). We also detect no sign of a seasonal dependence in the performance of bias correction and RF models (Supplementary Fig. 8). The resulting downscaled ERA5 data provide a complete annual series of hourly values for 1950–2019.
We estimate precipitation at the South Col also using ERA5. First, we linearly interpolate the reanalysis data to the location of the Phortse AWS5 and then compute the ratio of the total observed precipitation (Po) and ERA5 precipitation (PE) during the overlapping period (April 2019-November 2020). We then multiply all reanalysis precipitation by this scalar to produce a corrected precipitation series (PE') for Phortse 1950–2019:
To extrapolate to the South Col, we assume that precipitation decays exponentially with increasing elevation30. However, we recalibrate the regression using the Phortse and Basecamp AWSs because these new sites have weighing precipitation gauges protected by double alter shields5, and hence are less prone to under-catch error (Supplementary Fig. 9). Note that, as described below, the precipitation estimate is adjusted to an “effective” flux before being used to simulate glacier mass balance changes.
Mass balance
We use the precipitation, along with the other downscaled meteorological variables, to force the COSIPY model20 at hourly resolution for 1950–2019. First, we compute the effective precipitation (which implicitly includes the net effects of avalanching and wind transport, as well as correcting for any systematic bias in the downscaling/extrapolation method described above) required for the glacier to be in equilibrium for the period 1950–1959, iterating until the surface mass balance is zero. This is achieved when the precipitation is decreased by 65%. We then run two simulations with COSIPY. The first (referred to as the “snow” simulation) assumes a starting snowpack that is arbitrarily deep (20 m) to ensure that it remains present throughout the entire (70-year) simulation. We set the initial surface density of the snowpack to 350 kg m−3, the bottom density to 800 kg m−3, and linearly interpolate between. The second simulation (hereafter the “ice” simulation) uses the same effective precipitation but assumes no initial snowpack. However, snow is free to accumulate in the model in response to meteorological forcing. The algorithms and parameter values used in our application of COSIPY are outlined in Methods Table 2.
Melt
The surface melt rate depends on the surface energy balance (SEB):
where Q denotes energy flux (W m−2) and the subscripts h, l, lw, sw, g, and r refer to the sensible, latent, net longwave radiative, net shortwave radiative, ground, and precipitation heat fluxes, respectively. The fluxes are defined as positive when directed towards the surface. The energy consumed in melting (Qm) is also defined as positive, meaning the melt rate (M; mm w.e. s−1 or kg s−1) can be calculated:
in which H(Q,Ts) is a Heaviside function that returns a value of one unless both the sum of the first six terms in Eq. (6) (Qm = ∑Qi, with i indexing terms Qh to Qr) is positive and the surface temperature is also at the melting point; otherwise, it returns zero. The melt total over a period of ∆t seconds can then be expressed:
where P is the fraction of ∆t during which melting conditions occurred, and the overbar for energy component Qi indicates the mean value calculated during melting conditions. In terms of energy components Eq. (8) is the major driver of the amplification in melt totals between the snow and ice COSIPY simulations, increasing by a factor of 4.4; the energy sinks (sum of the remaining terms) amplify by a factor of 3.6 (Methods Fig. 3). The resulting amplification in mean melt rate \(\left( {\acute{A} = \frac{{\left( {{\sum} {\overline {Q_i} } } \right)_{{{{\mathrm{ice}}}}}}}{{\left( {{\sum} {\overline {Q_i} } } \right)_{{{{\mathrm{snow}}}}}}}} \right)\), though, is by almost a factor of 500. To understand this result, note that the proportional increase in melt rate can be written:
where \(\overline {Q_{{{{\mathrm{sw}}}}}}\) and \(\overline {Q_{{{{\mathrm{sinks}}}}}}\) are the mean energy gains and losses, respectively, during melt conditions in the snow simulation, and k and j are the proportional increases in these terms when transitioning to an ice surface (4.3 and 3.6, respectively). Critically, Eq. (9) reveals that \(\acute{A}\) is inversely proportional to the baseline melt rate in the snow simulation \(\left( {\overline {Q_{{{{\mathrm{sw}}}}}} - \overline {Q_{{{{\mathrm{sinks}}}}}} } \right)\). The very low melt rate in the snow scenario (3.3 mm w.e. a−1), therefore acts to amplify the numerator of in Eq. (9).
Sublimation and melt sensitivity to climate forcing
Total sublimation (S, mm w.e. or kg) can be written:
where ρ is the air density (kg m−3), U is the wind speed (m s−1), Ce is the turbulent exchange coefficient for moisture (dimensionless), ε is the ratio of gas constants for water vapor and air (0.622), Pa is air pressure (Pa), and Υ is relative humidity (fraction). The saturation vapor pressure for the surface (es) and the near-surface atmosphere (ea) are functions of the surface (Ts) and air temperature (Ta), respectively. If we assume that Ts = Ta (which is a reasonable simplification at the South Col where air temperature does not rise above 0 °C), and use the Clausius Clapeyron equation:
in which e0 is the saturation vapor pressure at the melting point, L is the latent heat of sublimation (2.83 × 106 J kg−1), and Rv is the gas constant for moist air (461 J K−1); Eq. (10) becomes:
which can be differentiated with respect to U, Ta, and Υ to explore the sensitivity of sublimation to changes in these meteorological parameters. In turn, the contribution of temporal trends \(\left( {\frac{{{\mathrm{d}}x}}{{{\mathrm{d}}t}}} \right)\) in these variables to the trend sublimation can be evaluated via the chain rule:
With:
To evaluate Eq. (13) we compute the derivatives (Eqs. (14)–(16)) using the mean meteorology at the South Col during the ERA5 reconstruction (1950–2019), and ∆t to the number of seconds in 1 year (3.2 × 107 s). We prescribe the turbulent exchange coefficient (Ce) using the output from the COSIPY snow simulation, dividing the simulated sublimation by \(\rho \;U(e_{{{\mathrm{s}}}} - e_{{{\mathrm{a}}}}\Upsilon )\frac{\varepsilon }{{P_{{{\mathrm{a}}}}}}\Delta t\) (see Eq. (12)).
Inserting these values into Eqs. (14) (16) yields:
We then estimate the time derivatives for Eq. (13) using the Theil-Sen slope estimation, yielding:
Summing these terms indicates a theoretical trend \(\left( {\frac{{{\mathrm{d}}S}}{{{\mathrm{d}}t}}} \right)\) of 0.27 mm w.e. a−2, in reasonably close agreement with the 0.22 mm w.e. a−2 derived from the COSIPY snow simulation and reported in the main text. This theoretical analysis also indicates that 82% of the trend can be attributed to increasing air temperature (41%) and declining relative humidity (41%), with strengthening winds explaining the remaining 18%.
An alternative (empirical) method to estimate the sensitivity of sublimation in the COSIPY snow simulation is to use multiple linear regression:
Where the slope coefficients (βx) are linear approximations of the derivatives, relating the changes in the annual mean of the meteorological variables to the total annual sublimation. Performing the regression (Supplementary Fig. 11) lends support to the interpretation from the theoretical analysis above, attributing 49, 26, and 25% of the sublimation increase to the trends in air temperature relative humidity, and wind speed, respectively.
In the main text, we highlight that sublimation and melt rates may differ in their response to climate forcing. To support this assertion, we repeat the sensitivity assessment above, evaluating the derivatives of the melt rate with respect to air temperature, wind speed, and relative humidity.
We simplify the analysis by assuming that the proportion of time that the surface is melting (P) is constant (see Eq. (8)). Although physically incomplete, we note that there is no temporal trend in P for the COSIPY snow simulation (p > 0.05 according to Seil-Then slope estimation). With this simplification, the sensitivity of the melt rate to changes in meteorological component x can then be written:
Wind speed, air temperature, and relative humidity appear in the expressions for the sensible, latent, and longwave heat fluxes (Qh, Ql, and Qlw, respectively):
In which we have assumed melting conditions (Ts = 273.15, e0 = 611.3 Pa; Lv is the latent heat of vaporization [2.5 × 105 J kg−1], and the longwave thermal radiation emitted by the snow surface is 312.5 W m−2); cp is the specific heat content of the air (1004.7 J kg−1 K−1). It has been concluded31 that the incident longwave flux Qlw↓ in the Himalaya may be estimated from Υ and Ta:
where the cx terms are empirically determined coefficients, whose value depends on cloudiness. Optimizing this expression for the South Col AWS, we found c1 = −17 (−168) W m−2, c2 = 0.73 (2.12) W m−2 %−1 and c3 = 0.57 (0.84) (dimensionless) for clear (cloudy) conditions.
The derivative of these fluxes with respect to air temperature is then:
Note that all terms in Eqs. (23)–(25) are positive, outlining the physical basis for why melt rates should increase with rising air temperature32.
The derivative of these fluxes with respect to relative humidity is:
Because all terms are positive in Eqs. (26) and (27), increases in relative humidity also drive increases in the melt rate.
The derivatives of the sensible and latent heat fluxes with respect to wind speed are then:
Because Ta is always less than 273.15 K during melt events at the South Col in the COSIPY snow simulation (Supplementary Fig. 12), \(e_0\;e^{\frac{L}{{R_{{{\mathrm{v}}}}}}\left( { - \frac{1}{{T_{{{\mathrm{a}}}}}} + \frac{1}{{273.15}}} \right)}\) must be less than 611.3 Pa. Hence, the last terms in Eqs. (28) and (29) are negative, and so increases in wind speed act to reduce the melt rate.
In summary, then, theory indicates that rising air temperatures should accelerate both sublimation and melt rates (Eqs. (15) and (24)). However, increases in wind speed and relative humidity will have opposite effects. Due to the persistence of freezing air temperatures during surface melt events, faster winds act to enhance sublimation (Eq. (14)) but reduce melting (Eqs. (28) and (29)), whereas increasing relative humidity amplifies melting (Eqs. (26) and (27)) but dampens sublimation (Eq. (16)).
Data availability
The downscaled meteorological data and COSIPY simulations are available from the corresponding authors on reasonable request.
Code availability
The COSIPY model is open source, and the code is available: https://github.com/cryotools/cosipy.
References
Hock, R. et al. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate (eds. Pörtner, H.-O. et al.) 131–202 (2019).
Immerzeel, W. W. et al. Importance and vulnerability of the world’s water towers. Nature 577, 364–369 (2019).
Mayewski, P. A., Perry, L. B., Matthews, T. & Birkel, S. D. Climate change in the hindu kush himalayas: basis and gaps. One Earth 3, 551–555 (2020).
Mayewski, P. A. et al. Pushing climate change science to the roof of the world. One Earth 3, 556–560 (2020).
Matthews, T. et al. Going to extremes: installing the world’s highest weather stations on Mount Everest. Bull. Am. Meteorol. Soc. 101, E1870–E1890 (2020).
Rowan, A. V. The ‘Little Ice Age’ in the Himalaya: a review of glacier advance driven by Northern Hemisphere temperature change. Holocene 27, 292–308 (2016).
Uglietti, C. et al. Radiocarbon dating of glacier ice: overview, optimisation, validation and potential. Cryosphere 10, 3091–3105 (2016).
Sneed, S. B. et al. New LA-ICP-MS cryocell and calibration technique for sub-millimeter analysis of ice cores. J. Glaciol. 61, 233–242 (2015).
Spaulding, N. E. et al. A new multielement method for LA-ICP-MS data acquisition from glacier ice cores. Environ. Sci. Technol. 51, 13282–13287 (2017).
Kaspari, S. et al. Recent increases in atmospheric concentrations of Bi, U, Cs, S and Ca from a 350-year Mount Everest ice core record. J. Geophys. Res. 114, 1–14, https://doi.org/10.1029/2008JD011088 (2009).
Kaspari, S. et al. Snow accumulation rate on Qomolangma (Mount Everest), Himalaya: synchroneity with sites across the Tibetan Plateau on 50–100 year timescales. J. Glaciol. 54, 343–352 (2008).
Mayewski, P. A. & Jeschke, P. A. Himalayan and Trans-Himalayan glacier fluctuations since AD 1812. Arct. Alp. Res. 11, 267 (1979).
Bolch, T. et al. The Hindu Kush Himalaya Assessment (eds. Wester, P., Mishra, A., Mukherji, A. & Shrestha, A. B.) 209–255 (Springer International Publishing, 2019).
King, O. et al. Six decades of glacier mass changes around Mt. Everest are revealed by historical and contemporary images. One Earth 3, 608–620 (2020).
Perry, L. B. et al. Precipitation characteristics and moisture source regions on Mt. Everest in the Khumbu, Nepal. One Earth 3, 594–607 (2020).
Liu, W. et al. Monsoon clouds control the summer surface energy balance on East Rongbuk Glacier (6,523 m Above Sea Level), the Northern of Mt. Qomolangma (Everest). J. Geophys. Res. Atmos. 126, e202JD0033998 (2021).
Takeuchi, N., Hori, Y., Furukawa, N., Yoshida, M. & Fujii, Y. Glacio-environmental aspects recorded in two shallow ice cores drilled in 1980 at accumulation area of Khumbu Glacier of Mt. Everest in Nepal Himalayas. Arct. Antarct. Alp. Res. 52, 605–616 (2020).
Hou, S. et al. Summer temperature trend over the past two millennia using air content in Himalayan ice. Clim. Past 3, 89–95 (2007).
Hersbach, H. et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049 (2020).
Sauter, T., Arndt, A. & Schneider, C. COSIPY v1.3 – an open-source coupled snowpack and ice surface energy and mass balance model. Geosci. Model Dev. 13, 5645–5662 (2020).
Cullen, N. J., Mölg, T., Kaser, G., Steffen, K. & Hardy, D. R. Energy-balance model validation on the top of Kilimanjaro, Tanzania, using eddy covariance data. Ann. Glaciol. 46, 227–233 (2017).
Stigter, E. E. et al. The importance of snow sublimation on a himalayan glacier. Front. Earth Sci. 6, 108 (2018).
Mölg, T. & Hardy, D. R. Ablation and associated energy balance of a horizontal glacier surface on Kilimanjaro. J. Geophys. Res. 109, D16104 (2004).
Wagnon, P., Ribstein, P., Francou, B. & Sicart, J. E. Anomalous heat and mass budget of Glaciar Zongo, Bolivia, during the 1997/98 El Niño year. J. Glaciol. 47, 21–28 (2001).
Francou, B., Vuille, M., Wagnon, P., Mendoza, J. and Sicart, J. E. Tropical climate change recorded by a glacier in the central Andes during the last decades of the twentieth century: Chacaltaya, Bolivia, 16°S. J. Geophys. Res. 108, 4154 (2003).
Collins M. et al. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds. Stocker T. F. et al.) (Cambridge University Press, 2013).
Litt, M. et al. Glacier ablation and temperature indexed melt models in the Nepalese Himalaya. Sci. Rep. 9, 5264 (2019).
Mölg, T. & Kaser, G. Springer Textbooks in Earth Sciences, Geography and Environment. 483–495 (Springer International Publishing, 2021).
Matthews, T. et al. Into thick(er) air? oxygen availability at humans’ physiological frontier on Mount Everest. iScience 23, 101718 (2020).
Salerno, F. et al. Weak precipitation, warm winters and springs impact glaciers of south slopes of Mt. Everest (central Himalaya) in the last 2 decades (1994–2013). Cryosphere 9, 1229–1247 (2015).
de Kok, R. J. et al. Measurements, models and drivers of incoming longwave radiation in the Himalaya. Int. J. Climatol. 40, 942–956 (2020).
Ohmura, A. Physical basis for the temperature-based melt-index method. J. Appl. Meteorol. 40, 753–761 (2001).
CCI, 2021. Climate Reanalyzer is a climate data access and visualization tool developed by the Climate Change Institute at the University of Maine. Maps of monthly reanalysis data from several models can be generated using the interface at https://climatereanalyzer.org/reanalysis/monthly_maps/.
Oerlemans, J. & Knap, W. H. A 1 year record of global radiation and albedo in the ablation zone of Morteratschgletscher, Switzerland. J. Glaciol. 44, 231–238 (1998).
Boone, A. Description du Schema de Neige ISBA-ES (Explicit Snow), Tech. rep., Centre National de Recherches Météorologiques, Météo-France, Toulouse (2004).
Foken, T. Micrometeorology, Berlin Heidelberg (Springer 2008).
Bintanja, R. & Van Den Broeke, M. R. The surface energy balance of Antarctic Snow and Blue Ice. J. Appl. Meteorol. 34, 902–926 (1995).
Xu, J. et al. A 108.83-m ice-core record of atmospheric dust deposition at Mt. Qomolangma (Everest), Central Himalaya. Quat. Res. 73, 33–38 (2010).
Mölg, T., Maussion, F., Yang, W. & Scherer, D. The footprint of Asian monsoon dynamics in the mass and energy balance of a Tibetan glacier. Cryosphere 6, 1445–1461 (2012).
Acknowledgements
This research was conducted through a partnership with National Geographic Society, Rolex, and Tribhuvan University, with approval from all relevant agencies of the Government of Nepal. We thank the communities of the Khumbu Region, Xtreme Climbers Treks and Expedition P. Ltd, Jiban Ghimire, and Shangri-La Nepal Trek Pvt. Ltd. The high-altitude Sherpa team included: Panuru Sherpa (Sirdar), Phu Tashi Sherpa, Pemba Sherpa, Urken Lendu Sherpa, Ila Nuru Sherpa, Fura Chetten Sherpa, Lakpa Gyaljen Sherpa, Pasang Sona Sherpa, Pasang Kami Sherpa, Nima Rita Sherpa, Tenzing Gyanjen Sherpa, Nawang Phinjo Sherpa, Phinjo Sherpa, and Gyaljen Dorji Sherpa. Dawa Yangzum Sherpa, Amrit Ale, Mark Fisher, Dirk Collins, and Eric Daft are also thanked for helping to ensure a successful and safe climb conducted with good humor. Many thanks to Sandra Elvin, Pete Athans, Aurora Elmore, Tyler Dinley, and many others of the National Geographic logistics and storytelling staff, the United States Embassy in Kathmandu, Fisher Creative, our fellow team members and all of the porters, people, and businesses in the Khumbu Valley. Radiocarbon analysis was conducted by Ling Fang from Paul Scherrer Institute at the Laboratory for the Analysis of Radiocarbon with the University of Bern AMS, Switzerland. ERA-5 reanalysis19 data files are freely available at the Copernicus Climate Change Service Climate Data Store (https://cds.climate.copernicus.eu/cdsapp#!/home). Ultra-high-resolution continuous laser sampling was conducted using the Climate Change Institute’s WM Keck Laser Ice Facility laser ablation inductively coupled plasma mass spectrometer (LA-ICP-MS) system. We thank the reviewers of this paper for their insightful suggestions. This paper is dedicated to Urken Lendu Sherpa, a member of our Summit team, who died climbing in 2021.
Author information
Authors and Affiliations
Contributions
P.A.M., M.P., T.M., and L.B.P. conceived the research and designed the study; P.A.M. was Everest Expedition Leader and Science Leader; M.P. recovered the ice core; L.B.P. and T.M. installed the automatic weather stations; T.M., P.K.S., T.C.S., and I.K. performed the energy balance modeling; M.S. provided the radiocarbon dating; E.K. conducted laser analyses and H.C. and M.P. prepared samples; M.P., P.A.M., T.M., and L.B.P. wrote the manuscript with contributions from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Potocki, M., Mayewski, P.A., Matthews, T. et al. Mt. Everest’s highest glacier is a sentinel for accelerating ice loss. npj Clim Atmos Sci 5, 7 (2022). https://doi.org/10.1038/s41612-022-00230-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-022-00230-0