Introduction

Growing water scarcity, changing terrestrial hydrologic cycles, and their impacts on ecological function have generated considerable interest in the origins of precipitation1,2. Such interest is particularly strong for the tropics, where local (recycled) water significantly impacts precipitation. For instance, it is estimated that 25–35% of rainfall in the Amazon basin, and >50% in the Congo basin, comes from nearby land evapotranspiration3,4. These levels of recycling are caused not only by the high evapotranspiration rates that result from tropical forests, but also are influenced by regional atmospheric circulation patterns and topography5. Climate change and deforestation are linked to rainfall reductions over the Asia monsoon region and the Amazon6,7,8, and the tropical climate has changed dramatically over time9,10,11. Accordingly, as policymakers seek to forecast water availability, accurate recycling models are crucial for informed decision making.

Precipitation recycling refers to the mechanism by which evapotranspiration from some pre-defined source is later re-precipitated within the very same source region12. Despite its importance, precipitation recycling is challenging to measure directly. While precipitation stable isotopes have been a recent focus of efforts to measure recycling because they exist as natural tracers in precipitation samples, they typically are not collected for global studies and can be influenced by many environmental effects that may obscure the relationship between isotope measurements and recycling13.

In response, recent research efforts have focused on developing models of precipitation recycling which are not subject to these drawbacks. The Mass Balance model, which focuses on the moisture fluxes in and out of a pre-defined region, is one such example. The precipitation recycling metric produced by the Mass Balance model is the regional recycling ratio (RRR), defined as the fraction of locally sourced precipitation occurring over a pre-defined region. Originally developed to study the hydrologic cycle of Russian river basins12, the RRR has since been applied worldwide to characterize recycling phenomena from several large river basins including the Amazon and the Mississippi14,15. While the RRR is computationally efficient, it fails to consider short-timescale processes critical to moisture tracking, such as diurnal timescales16. Moreover, the RRR is influenced by both region size and shape14, making irregular boundaries such as coastlines or political borders particularly challenging to evaluate. Responding to these shortcomings, modelers developed alternative methods to instead compute precipitation recycling by tracking moisture teleconnections16,17,18. In their estimates, these particle-tracking models consider moisture originating from any land evaporation source, not just from within a pre-defined region. In addition, they are forced using reanalysis data at a sub-daily resolution, thus capturing diurnal patterns. However, these reanalysis products, which resolve precipitation, evaporation, and wind fields, are subject to any biases that exist in such data19,20. The resulting computed entity in these models is known as the Land Recycling Ratio (LRR), which is the percentage of precipitation in each region sourced from land evaporation.

Given the growing diversity in approaches to characterizing precipitation recycling, a means by which to constrain and evaluate recycling models has become increasingly desirable, especially since precipitation recycling is difficult to measure at global scales21,22,23. A leading candidate to provide this observational value is a precipitation isotope quantity known as deuterium excess (d-excess)24, computed using the following equation:

$${{{\mathrm{d}}}} - {{{\mathrm{excess }}}}\left( \textperthousand \right){{{\mathrm{ }}}} = \delta ^2H - {{{\mathrm{ }}}}8{{{\mathrm{ }}}} \ast \delta ^{18}O$$
(1)

where \({\mathbf{\updelta}}^2H\) and \({\mathbf{\updelta}}^{18}O\) are the deuterium and oxygen-18 contents measured from a water sample24. Precipitation d-excess is known to correlate with land recycling because of kinetic fractionation that modifies isotopic signatures after evaporation and condensation25,26,27,28. However, obstacles limit the direct application of d-excess to constraining large-scale modeled recycling estimates. For instance, ground-based precipitation isotope observations have historically been sparse29. Moreover, non-recycling influences on d-excess, such as sub-cloud evaporation (the re-evaporation of falling precipitation)21, may influence the degree of model-observation agreement.

Even while facing these barriers, some case studies have succeeded in relating recycling phenomena to seasonal d-excess dynamics30,31,32. It is in the context of these encouraging results that in this investigation, we leverage extensive tropical isotope data to attempt a more spatially comprehensive analysis by quantitatively measuring spatio-temporal agreement between models of precipitation recycling and observations of d-excess across the entire tropics. We also explore the effects of observation frequency, vegetation density, and seasonal precipitation patterns on our results. We hypothesize that (1) recycling ratios generated from a representative model should correlate with the spatial and temporal variations in d-excess (H1), given the sensitivity of d-excess to the phase changes that occur during precipitation recycling; (2) the particle tracking models will better predict d-excess by capturing a more representative set of land evaporation sources (H2) because unlike the Mass Balance method (RRR), the particle tracking approach to computing the recycling ratio (LRR) theoretically accounts for all global sources of land evaporation; and (3) increased spatial coverage of d-excess sampling data will improve model-observation agreement (H3), as the mismatch in scales between point-like d-excess observations and large-scale recycling model estimates is resolved by averaging over larger datasets.

Results

Spatiotemporal intercomparison of recycling models

Before introducing d-excess as an observational proxy for recycling, we first compared the three precipitation recycling models considered in this study, Mass Balance (RRR)14, WAM-2layers (LRR)17, and UTrack (LRR)18, across the Köppen-Geiger (KG) climate subzones that occur in the tropics33. The mean recycling ratios for each model were first plotted side by side, showing that recycling ratios are generally higher for LRR than RRR (Fig. 1). We anticipated this pattern since the LRR is defined to account for all land evaporation, while the RRR accounts for land evaporation solely within a bounded region. Furthermore, we evaluated spatio-temporal agreement among different models using Kendall’s rank correlation coefficient (\(\tau = 1\) is a perfect monotonic correlation; \(\tau = - 1\) is a perfect anti-correlation), which is helpful in cases where a linear relationship is not guaranteed34. Model agreement between particle tracking and Mass Balance models was modest (WAM-2layers \(\bar \tau = 0.37\), Fig. 2a; UTrack \(\bar \tau = 0.27\), Fig. 2b), although results showed higher levels of spatial agreement between WAM-2layers and UTrack particle tracking models (\(\bar \tau = 0.67\), Fig. 2c). We largely expected this behavior, since the two models computing the LRR should agree more often with each other than with model predictions of the RRR. All models demonstrated high time-series correlation across most of East Africa but showed differences in West Africa, where the particle tracking models displayed anti-correlated behavior against the Mass Balance model.

Fig. 1: Mean annual recycling ratios.
figure 1

The mean annual recycling ratio is visualized from 2002 to 2018 for UTrack (a), WAM-2layers (b), and Mass Balance (c) within the tropical Köppen–Geiger climate zones. Identical color scales are used for each plot, but the range of the Mass Balance color gradient is reduced from 0–1 to 0–0.05 due to the generally smaller values taken on by the regional recycling ratio (RRR) in comparison to the land recycling ratios (LRRs).

Full size image
Fig. 2: Model intercomparison of moisture recycling estimates.
figure 2

The scatter plots shown above represent the grid-by-grid comparison of mean annual estimates of the recycling ratio for the entire 2002–2018 analysis period, where the black dashed line indicates a 1:1 correspondence. The right panel includes two plots per model comparison: the difference in mean annual estimates for the two models (top) and corresponding rank-based time-series cross-correlation between model estimates (bottom). Panel (a) shows WAM-2layers vs. Mass Balance, panel (b) shows UTrack vs. Mass Balance, and panel (c) shows UTrack vs. WAM-2layers.

Full size image

WAM-2layers and UTrack, the two models that track water vapor tracers, had the highest level of inter-model agreement (\(\bar \tau = 0.67\)). The LRRs reported in WAM-2layers were on average higher than UTrack by \(5.4 \pm 0.1\!\%\). Furthermore, while WAM-2layers estimated greater recycling levels in Central America and Asia, UTrack predicted higher recycling in Central Africa and South America (Fig. 2c). These discrepancies could be due to differences in numerical integration techniques or vertical model resolutions, both of which have previously been linked to divergent outcomes in model outputs18. For example, while the UTrack model is a Lagrangian model that is forced with reanalysis data for 25 vertical atmospheric layers, the WAM-2layers model is an Eulerian model forced with data for two layers. The model forcing data also differ in their horizontal resolutions, where the UTrack model uses ERA535 climate forcing data at a 0.25-degree resolution to drive its model, while WAM-2layers uses ERA-Interim36 at a 1.5-degree resolution. The ERA-Interim reanalysis has been found in regional studies to exhibit greater biases in tropical precipitation than ERA5, which is a surface flux that directly impacts measurements of precipitation recycling20. These different features potentially compound to produce divergent model results.

All models were highly correlated in small landmass regions surrounded by water, such as the Philippines and Central America, likely because in this regime, the LRR closely approximates the RRR due to the lack of nearby land evaporation sources. While the LRR can be impacted by moisture parcels traveling from distant land evaporation sources, the RRR is strictly dependent on local gridded moisture fluxes. As a result, the particle tracking and Mass Balance model are less related across larger landmasses such as South America and Africa, meaning that the behavior of the RRR diverged from that of the LRR within inland continental regions.

Climatological comparisons of model recycling ratios to deuterium excess

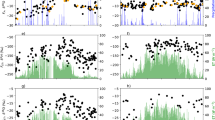
To test whether d-excess would be correlated with model recycling estimates (H1) and whether particle tracking models would see a stronger correlation with d-excess (H2), we analyzed their climatological signals within each tropical KG subzone. As expected, we found statistically significant (\(\alpha = 0.05\)) model-observation agreement in several climatological comparisons, including the tropics overall (Fig. 3a) for WAM-2layers (\(\bar \tau = 0.55\)) and Mass Balance (\(\bar \tau = 0.61\)); the Af subzone for UTrack (\(\bar \tau = 0.52\), Fig. 3b); and the Am subzone for Mass Balance (\(\bar \tau = 0.70\), Fig. 3c). However, no model achieved a statistically significant correlation in the Aw or As subzones (Fig. 3d, e). In fact, the mean rank correlations reported for the climatological analyses done in the Aw and As subzones were mostly lower than the mean rank correlations reported for other regions. One possible explanation for the lower agreement in the Aw and As subzones is the strong seasonal precipitation signal in these regions leading to higher divergence of d-excess and recycling across the annual precipitation cycle, especially during the dry seasons. Accordingly, we found support for hypothesis H1 within Af and Am, but not for Aw or As.

Fig. 3: Climatological cross-comparison of model recycling ratios against observational d-excess values across the tropical region.
figure 3

The mean d-excess value across all stations and years (brown) is compared against the corresponding recycling ratio estimates given by UTrack, WAM-2layers, and Mass Balance models (blue). From top to bottom, the results are arranged by row according to their Köppen–Geiger subzone (A, Af, Am, Aw, As), and the results for each recycling model are given in a new column (UTrack, WAM-2layers, Mass Balance). Kendall’s Tau rank cross-correlation coefficient is computed between climatological signals of recycling ratio and d-excess. The expected correlation is reported (\(\bar \tau\)) as well as the 95% confidence interval.

Full size image

In addition to finding variability in model-observation agreement between climate subzones, we also found that recycling models demonstrated different strengths in correlation for the same region. Somewhat surprisingly, the Mass Balance model sometimes showed higher or equal climatological agreement when compared to WAM-2layers or UTrack for a given subzone. For example, in the tropics overall (Fig. 3a), WAM-2layers agreement (\(\bar \tau = 0.55\)) was similar to Mass Balance (\(\bar \tau = 0.61\)). It also was the highest correlated model in Am (\(\bar \tau = 0.70\), Fig. 3c), although the UTrack model was more highly correlated with Af (\(\bar \tau = 0.52\), Fig. 3b). Seemingly, while the RRR does not account for distant land evaporation, it still reports relatively strong agreement with d-excess when compared to the particle tracking results, calling hypothesis H2 into question and perhaps indicating that this process does not play an important role in precipitation recycling for some regions.

Finally, we examined how other non-recycling influences might impact climatological agreement beyond the amount effect. For example, canopy interactions with falling precipitation can change isotopic compositions of precipitation before it reaches the GNIP sampling station37,38,39. Accordingly, dense canopies surrounding d-excess observation sites can further de-couple stable isotope signatures from land and ocean evaporation. To study this effect, we removed observations from regions with outlier vegetation coverage, which we consider for this study to be greater than the 90th percentile value of total leaf area index (TLAI) for all points sampled (>8.6 m2/m2), from the climatological analysis of the overall tropics (Fig. 4). We find that this intervention improved agreement for both UTrack (\(\bar \tau = 0.48\), Fig. 4b) and WAM-2layers (\(\bar \tau = 0.58\), Fig. 4b), and all three models showed statistically significant agreement with d-excess signal. Beyond vegetation, we also looked for evidence that ENSO or extreme precipitation events might impact our climatology-based analysis, both of which are known to influence isotopic composition and its correspondence with recycling40,41. However, neither uniformly improved climatological agreement for our tropical analysis. Accordingly, the robust correspondence between d-excess and recycling ratios across several models and tropical regions supports hypothesis H1, but confounding factors such as vegetation coverage and seasonal precipitation are shown to further mediate this agreement at regional to local scales.

Fig. 4: Climatological comparison with dense vegetation outliers removed.
figure 4

The overall tropical climatological comparison from Fig. 3a is replicated in panel (a). Panel (b) shows an identical analysis, but where observations which are associated with the >90th percentile of total leaf area index (TLAI) are removed from the analysis.

Full size image

More stations increase model-observation agreement

To further test hypothesis H3, we set out to understand how spatial coverage (i.e., number of isotope stations sampled in each month) could influence model-observation agreement. First, we computed the rank correlation coefficient between the co-located mean recycling ratio and d-excess values for all three models and all 204 months in the analysis period. Then, we systematically selected months to ignore in our analysis according to the minimum station sample size targeted for each month and re-computed the correlation coefficient. Without filtering out low-coverage months, only UTrack (\(\bar \tau = 0.17\), Fig. 5a) and WAM-2layers (\(\bar \tau = 0.14\), Fig. 5b) demonstrated a statistically significant relationship between monthly mean recycling estimates and d-excess. However, with a station sample size filter in place, the Mass Balance model also achieved a statistically significant agreement with d-excess data starting at a minimum station sample size of 7 (Fig. 5c).

Fig. 5: Station sample size analysis.
figure 5

Kendall’s Tau rank correlation is computed between mean d-excess and precipitation recycling estimates across all tropical stations and for each recycling model for the monthly time-series from 2002 to 2018. The average correlation coefficient (black solid line) and corresponding 95% confidence interval (solid gray fill) are constructed for each minimum station sample size value. The corresponding sample size is reported (brown dashed line) for each analysis.

Full size image

Overall, we found that greater station sample sizes generally corresponded to increased model-observation agreement, supporting hypothesis H3. This statement was especially true for the Mass Balance approach, as the addition of a sample size filter made the results statistically significant with moderately correlated behavior that was comparable to UTrack and WAM-2layers. However, for minimum station sample sizes of \(n \,>\, 10\), the total months included in the analysis dropped precipitously, eventually incorporating just a small fraction (<25%) of the original total number of months that were used. In this regime, the uncertainty in rank correlation estimates grew substantially, masking any underlying trend. Therefore, we stopped the station sample size analysis for each model when the results were not statistically significant (\(p\, >\, 0.05\)). More d-excess station observations would be needed to better understand how model-observation agreement changes in large station sample sizes and to reduce statistical uncertainty.

Discussion

This study leveraged recently available datasets to test the relationship between observed d-excess signal and estimated precipitation recycling ratios across the tropics. We compared three contemporary recycling models with different methodologies and showed how their estimates of precipitation recycling varied, in part due to the uncertainty propagated by measurements and because of differences in their computational methods. We then used a climatological analysis to evaluate the extent to which d-excess observations aligned with predicted recycling ratios for each model and tropical climate subzone.

We found strong agreement between d-excess measurements and model-generated recycling ratios for a wide range of models and tropical regions, which supports our hypothesis that d-excess concentrations would be shown to track recycling behavior (H1). Due to the promising outcomes of our approach, future studies may find it instructive to incorporate d-excess into next-generation recycling models, Earth System Models that include water isotopes42, or to use it as a benchmark to evaluate model performance. However, our analysis highlights two possible influences on model-observation agreement that might complicate the direct application of d-excess to modeled recycling values at global scales: (1) a lack of sufficient isotope data and (2) a robust seasonal precipitation pattern in certain Köppen–Geiger climate subzones. Within the tropics, the first of these reasons is most likely to be influential within the As subzone, where measurements are significantly less abundant (\(n = 233\)) than the other three: Af (\(n = 891\)), Am (\(n = 779\)), and Aw (\(n = 1498\)). Large sample sizes could also contribute to the higher agreement found in the overall tropics comparisons, which showed strong model-observation correlations for multiple models. However, a lack of data is unlikely to be the complete story since the Aw subzone demonstrated no statistically significant model-observation agreement but had a larger sample size than any other region.

Accordingly, we identify seasonal precipitation patterns as another likely mediating factor due to the higher potential for sub-cloud evaporation effects. Sub-cloud evaporation is an atmospheric process whereby water vapor gets re-evaporated while raining down onto the ground. While sub-cloud evaporation can occur over sub-daily timescales, its cumulative impact is detected in our analysis on the monthly timescales at which the GNIP stations measure. With increasing precipitation levels, the d-excess measured at ground level will approach the d-excess as measured at the cloud base and thus be less influenced by sub-cloud evaporation—a phenomenon that has been termed the amount effect21. Therefore, with lower precipitation, d-excess becomes less related to the recycling signal. The amount effect could explain why climate subzones with extended dry periods, such as Aw and As, generally show poor model-observation agreement, while subzones with intermittent (Am) or non-existent (Af) dry periods demonstrated stronger correlations. While our goal in this study was to compare observation data directly to recycling estimates over a large region such as the tropics, future work could involve using a correction procedure on d-excess data to further probe the influence of sub-cloud evaporation on model-observation agreement at finer spatial scales in climates with a distinct dry season30.

In addition to seasonal precipitation, we identify vegetation interactions with precipitation as a further influence on our climatological analysis. Dense vegetation coverage in the face of incoming rainfall is known to influence precipitation isotope compositions. Local d-excess values are influenced by amplified rates of interception and transpiration in the forest canopy, while rates of evaporation at the soil surface are simultaneously suppressed37,38,39. Furthermore, the forest vegetation can be a significant driver of local precipitation, even by potentially initiating a wet season43. These mechanisms serve to further confound the relationship between precipitation recycling and d-excess. This is reflected by the fact that removing outlier observations corresponding to particularly dense canopies improved our climatological analysis. A similar analysis restricting the dataset based on ENSO influences (removing months associated with SOI > 1.5 and SOI > 3.0) or extreme precipitation (removing observations associated with >90th percentile monthly precipitation rates) did not clearly improve climatological agreements, even though both have been identified as potential mediators of precipitation isotope composition40,41. This could be due to strength of their effects depending greatly on regional conditions, along with interannual variability in the case of ENSO, which would be less influential at the global, climatological scales of our analysis. For example, in one region, an ENSO event could dramatically change precipitation, but for the same region in another year with the same magnitude ENSO effect, there may be a much smaller impact. Furthermore, our study includes a substantial number of stations in the African tropics, which are farther away from the source region of ENSO (tropical Pacific).

The climatological analysis was also instructive in testing hypothesis H2 that particle tracking models demonstrate stronger agreement with d-excess observations than the Mass Balance model. Differences between the LRR generated with WAM-2layers and UTrack may result from UTrack’s greater spatial resolution, or the different numerical integration approaches used by the two models. They could also be due to UTrack’s reliance on ERA5, which has been shown to exhibit less bias in some tropical regions than ERA-Interim, used by WAM-2layers20. Although the UTrack model performed best in the Af subzone (\(\bar \tau = 0.52\), Fig. 3b), we found that in the Am subzone, the Mass Balance model showed a higher correlation with d-excess (\(\bar \tau = 0.70\), Fig. 3c) than either particle tracking model. In addition, for the tropics overall (Fig. 3a), the Mass Balance model exhibited similar correlation with d-excess (\(\bar \tau = 0.61\)) to another particle tracking model, WAM-2layers (\(\bar \tau = 0.55\)). These results offer evidence against H2 since the model performance of particle tracking models was not clearly superior. Such evidence suggests that distant land evaporation may have less impact on d-excess than land evaporation from more proximal sources. Specifically, moisture parcels that undergo longer transit paths may have more opportunities to experience phase changes and other environmental effects that could impact the isotopic composition of precipitation and reduce the relative influence of land recycling on d-excess values. For example, there would be more opportunities to mix with other moisture sourced from open water evaporation from vegetation canopies, urban areas, lakes, or other sources that do not cause the same isotope fractionation as traditional land evaporation. This theory could be further tested by assessing model-measurement agreement as a function of source area, but such analysis would require a much finer spatial scale (e.g., sub-kilometer) investigation than what we do here and is thus beyond the scope of this work.

Finally, the station sample size analysis demonstrated support for hypothesis H3 since increased station sample sizes generally improved model-observation agreement. This result can be explained by confounding factors that influence precipitation isotope composition at local scales. The International Atomic Energy Agency (IAEA) Global Networks in Precipitation (GNIP) standards suggest that measurement stations should be placed as far away as possible from trees and buildings29. This guidance is intended to reduce the likelihood that incoming precipitation will be intercepted on its way to the detector, which would introduce bias into the collected sample. Even so, these effects can be hard to eliminate completely, especially for certain locations with particularly dense vegetation coverage like those in the tropics. In contrast, recycling models report estimates at a grid-scale, which are not subject to local interception effects. Accordingly, by averaging across all stations in a climate subzone for a given month, the differences between models and observations were diminished, and a more robust spatio-temporal pattern of agreement emerged. A similar result has been found in the past when comparing global models of precipitation isotope quantities to GNIP data44. Nevertheless, because existing isotope measurement stations remain sparse, the effectiveness of such comparisons is currently limited to well-studied regions where estimates from many stations (\(n \,>\, 10\)) and months (\(n \,>\, 50\)) are available. Additional isotope station measurements would be ideal to explore how sample size impacts model-observation agreement in greater detail.

In summary, our study serves to further illustrate the relationship between precipitation recycling models and d-excess observations by studying their correlation under a variety of conditions. We found that although these relationships were statistically significant in several analyses, strong seasonal precipitation patterns and observation-model mismatches in scale reduce agreement. To further increase the utility of d-excess in evaluating recycling, we encourage the addition of precipitation isotope data to publicly available databases--especially in under-sampled tropical regions such as the As climate subzone and the Southern Hemisphere tropics. A denser observation network will enable researchers to continue to probe the sources of uncertainties in d-excess and recycling ratios and how they vary with environmental conditions that impact precipitation and scale. We also encourage the use of more regional or local studies to examine the impact of smaller-scale influences on model-measurement correspondence, such as extreme precipitation events and ENSO signals, which are more pronounced at these resolutions.

Methods

Defining the tropics

For the purposes of this study, we constrained our analysis to the humid tropics, as defined according to the Köppen–Geiger classification zones: rainforest (Af), monsoon (Am), winter dry (Aw), and summer dry (As). These climate zones are based on mean climate conditions from 1951 to 200033. A map of the tropics, along with the location of each precipitation isotope sample point and the four climate zones, is shown in Supplementary Fig. 1.

Generating mass balance recycling estimates

The first modeled recycling estimate in this study was derived using the grid-based Mass Balance method14. The Mass Balance equation used to calculate the regional recycling ratio (RRR) is shown in Eq. 2:

$$RRR = \left( {1 + \frac{{2F^ + }}{{ETA}}} \right)^{ - 1}$$
(2)

where ET is the evapotranspiration flux (kg m−2 s−1), A is the area of the region (m2), and F+ is the moisture influx (kg s−1), which is calculated using Eq. 3:

$$F^ + = - {\int}_{\lambda _{in}} {\left( {\vec Q \cdot \hat n} \right)} d\lambda _{in}$$
(3)

where \(\lambda _{in}\) represents the boundary of interest, \(\vec Q\) is the moisture flux field (kg m−1 s−1), and \(\hat n\) is the normal unit vector (unitless)13.

The moisture flux field was taken from the ERA5 reanalysis product35. In this dataset, the monthly mean vertical integral of eastward moisture vapor flux and monthly mean vertical integral of northward moisture vapor flux were used as the zonal and meridional components, respectively, of the moisture flux field, interpolated at a regular grid resolution of 0.25 degrees. Using this field, the moisture influx was then computed at a 1-degree grid resolution by evaluating the line integral in Eq. 3. This result was then used in Equation 1, along with evapotranspiration data from ERA5, to compute each region’s recycling ratio. The result was a collection of monthly mean regional recycling ratios for each 1-degree grid across the humid tropics, from January 2002 to December 2018.

Generating WAM-2layers recycling estimates

Recently, researchers forced the WAM-2layers model using data from the ERA-Interim reanalysis36 to generate a database of 1.5 × 1.5-degree moisture teleconnection estimates between 79.5 degree N and 79.5 degree S latitude, enabling the determination of a monthly history on the fate of evaporation originating from land-cells45. The WAM-2layers model is an Eulerian tracking model in which the atmosphere is described with two vertical layers to account for vertical shear17. The dataset is generated with 3-hourly input data of evaporation and precipitation and 6-hourly input data of the wind components, surface pressure, total water column, total water vapor column and the vertical integral (all in eastward and northward direction) of the water vapor flux, cloud liquid water flux and cloud frozen water flux45. The database provides interannual estimates of the distribution of precipitation sources associated with each basin. To compute the land recycling ratio (\(LRR_{WAM - 2layers}\)) over a given 1.5-degree grid cell, the contributions to precipitation in the grid-cell of interest from each basin \((P_in_i)\)were summed and divided by the total precipitation as observed in ERA-Interim (\(P_{tot}\)). The monthly mean LRR was computed for each month between 2002 and 2018 using Eq. 4:

$$LRR_{WAM - 2layers} = \frac{1}{{P_{tot}}}\mathop {\sum}\nolimits_{all\;sources} {\left( {P_1n_1 + P_2n_2 + P_3n_3 + ...} \right)}$$
(4)

where \(P_{tot}\) is the total precipitation observed in the region, and \(P_in_i\) is the component of precipitation in the region that can be attributed to an arbitrary basin, which are summed for all possible land evaporation sources. While the other two recycling estimates were generated using data from ERA5, it has been shown that evaporation and precipitation values are similar between ERA5 and ERA-Interim reanalysis products45. Therefore, WAM-2layers should be comparable to UTrack and Mass Balance approaches, which both rely on ERA5 for input data.

Generating UTrack recycling estimates

Like WAM-2layers, the UTrack model has been used to produce public databases of moisture teleconnection46. However, the UTrack model uses Lagrangian, instead of Eulerian, numerical integration and divides the vertical component of transport into more atmospheric layers (25 layers) than WAM-2layers. The dataset is generated with hourly input data of evaporation, total precipitation, wind components, specific humidity and total precipitable water, all with a spatial resolution of 0.25 × 0.25 degree. Analogous to the WAM-2layers approach, UTrack computes the LRR by adding all global contributions of land evaporation to precipitation over a select region, then divides this sum by the total monthly precipitation. Running the model using ERA5 reanalysis data, the monthly mean land recycling ratio (\(LRR_{UTrack}\)) was reported on the 1.0-degree grid-scale spanning from 2002 to 2018. The results and model settings specific to this run were included as a supplement to this paper.

Monthly deuterium excess measurements

To compute d-excess, this study used water isotope measurements from the International Atomic Energy Agency’s Global Network of Isotopes in Precipitation (GNIP) database29. From 2002 to 2018, 90 stations reported monthly measurements within the A Köppen–Geiger (KG) tropical climate zone. The breakdown of station location by KG subzone was 22 stations in Af, 41 stations in Aw, 23 stations in Am, and 4 stations in As. Typically, stations provided measurements of \(\delta ^2H\) and \(\delta ^{18}O\), which were collected once per month, and plotted in Supplementary Fig. 2. The resulting mean water line, 10.39, was slightly higher than the global mean water line of 10, as expected for the tropics47. As expected, the amount effect was clearly observed in the GNIP sample, where a scatter plot shows the characteristic asymptote of d-excess towards the meteoric water line as precipitation increases (Supplementary Fig. 3). These isotope quantities were used in Equation 1 to calculate d-excess. To generate monthly estimates for d-excess, precipitation isotope measurements were averaged across every station which reported an estimate of monthly isotope concentrations for a given collection period. This process was repeated for all 204 months between 2002 and 2018. To justify the use of this dataset in our study, we assessed whether the climate and geography of isotope stations was representative of the global tropics. We compared their geographical distribution (Supplementary Fig. 4) and found that certain geographical regions, such as the As climate subzone and the Southern Hemisphere tropics, are under-represented in the dataset. We also probed the representativity of our sample dataset with respect to surface fluxes, such as precipitation and evapotranspiration rates. We find that our sample generally overrepresents locations with high magnitude precipitation and evapotranspiration, but that the distribution of our sample overlaps considerably with the tropics overall (Supplementary Fig. 5). While the sample median rates for evapotranspiration and precipitation differ from the tropics, their values lie firmly within the interquartile range for the overall region. Furthermore, the 10th and 90th percentile whiskers for both precipitation and ET match closely between sample locations and the tropics, suggesting that there is significant overlap between the typical values in both datasets. Finally, we tested the correspondence between GNIP measurements of monthly precipitation and co-located ERA5 estimates of monthly precipitation for each observation in the dataset. While we find relatively high error between individual GNIP observations and their ERA5 estimates (Supplementary Fig. 6a), the overall distribution of their values is highly similar (Supplementary Fig. 6b), suggesting that the datasets are congruent at large (global) spatial scales.

Model intercomparison

The model intercomparison study is designed to assess the extent to which a given recycling model pair agreed in their estimates of the recycling ratio. Each model time-series pair is compared via cross-correlation using Kendall’s Tau rank correlation coefficient as a comparison metric. A rank correlation metric was chosen because the expected relationship between models is sometimes unclear. For example, the relationship between RRR and LRR is not obviously linear, so Pearson’s coefficient would not be appropriate. For example, while d-excess would differentiate between a parcel of moisture that evaporates from land twice versus only once, the recycling ratio makes no such distinction. For each 0.5-degree with estimates recorded from both models, there were 204 months of data from 2002 through 2018. The estimates that each month provide were compared in time using Kendall’s Tau as described in Eq. 5:

$$\tau = \frac{{2(c - d)}}{{n(n - 1)}}$$
(5)

where \(\tau\) is the rank correlation coefficient, c is the number of concordant pairs of observations, d is the number of discordant pairs of observations, and n is the total number of observation pairs34.

Model results were also compared using a grid-by-grid difference in mean annual recycling estimates to compute relative bias between models within each model pair. These results were also visualized using a scatterplot, with a rank correlation coefficient used to show the general agreement between model pairs.

Climatological analysis

The climatological analysis was designed to test hypotheses H1 and H2, which both predict the extent to which model-generated recycling ratios will correlate with ground-based d-excess measurements. For each month (January 2002 to December 2018), any d-excess observations reported within the analysis region of interest are paired with the co-located monthly recycling estimate for the same month and year. Any coastal d-excess measurements that do not have a corresponding recycling measurement are omitted from the analysis. After all observations of d-excess are accounted for, the paired data are averaged according to month, from January to December. The averaging process produces two climatological signals for comparison, which are specific to the region and recycling model that were used in the procedure. Originally, the raw signals were smoothed using a three-month moving window designed to reduce inhomogeneities that might disturb the physical climate signal48,49, but this was found to have limited benefit. The climatological analysis procedure was repeated for all three-recycling model estimates and by restricting the analysis to each climate subzone within the tropics (A, Af, Am, Aw, As). The 95% confidence interval of Kendall’s Tau rank cross-correlation coefficient between the climatological signals was also computed for each signal that was generated. Finally, we repeated our procedure for climatological analysis once more in the overall tropics, but this time removing all observations which corresponded to a total leaf area index in the 90th percentile or higher for the population of GNIP sampling sites. The total leaf area index was computed by retrieving from ERA5 the values of the high vegetation and low vegetation leaf area indices co-located at each GNIP sample site and adding these two components together.

Station sample size analysis

The station sample size analysis was designed to test hypothesis H3, which predicts that an increase in spatial coverage of d-excess observations will improve the overall agreement between model-generated recycling ratios and d-excess values. First, for each of 204 months from 2002 through 2018, the mean d-excess from all reporting stations was aggregated. Then, the recycling ratios for the grid cells co-located with the d-excess measurement station were also aggregated. These monthly time-series were compared by constructing a 95% confidence interval of Kendall’s Tau rank cross-correlation. The procedure was then repeated for each minimum station sample size of N such that all months during the analysis period where at least N stations reported a d-excess measurement were included in the cross-correlation computation.

Code base

All analysis code base was written in Python50 on the standard Anaconda Distribution51 of Jupyter Notebook52. Kendall Tau statistics were computed using Dr. Wang’s “correlation” library53.