Introduction

Weather and climate extremes pose substantial risks to people, property, infrastructure, natural resources and ecosystems1,2,3. Although a majority of risk assessment studies have focused on single stressor hazards occurring in specific regions, the Intergovernmental Panel on Climate Change (IPCC) Special Report on Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation (SREX) highlights the importance of considering compound extremes resulting from the simultaneous or sequential occurrence of multiple climate hazards in the same region, for improved modeling and risk estimation of their impacts4. Since then, several studies have analyzed the risks and mechanisms of such compound events5,6,7,8,9. Another emerging category of compound events that involve the simultaneous occurrence of extremes across multiple regions, referred to as spatially compounding extremes, is gaining prominence due to the potential for their cascading impacts on the global food system, disaster management resources, international aid, reinsurance industries, and the global economy10,11,12.

Spatially compounding climate extremes across multiple global breadbaskets, regions that contribute substantially to global food production, can have aggregate impacts on global food availability and security7,13. The risk of co-occurring adverse climate conditions across multiple wheat, maize, and soybean producing regions has increased over the last four decades, highlighting the potential for simultaneous breadbasket failure14. In the absence of agricultural adaptation to climate change, projected climate changes will likely exacerbate the risk of crop failures across multiple breadbaskets. For instance, projected warming is likely to increase the co-occurrence of warm and dry extremes over multiple croplands and pastures7, and is also expected to amplify the risk of synchronous failures across major maize producing regions12. Such synchronous shocks could trigger international food price spikes and disrupt trade infrastructure, which could amplify threats to food security12,13,15, particularly in developing countries, where the population is already more vulnerable and food insecure16. In addition, compound extremes are likely to have amplifying negative impacts on insurance industries that integrate impacts across multiple sectors, and reinsurance industries that additionally integrate impacts across different regions10. Their increasing occurrence and associated losses could limit the profitability of insurance companies, which could have cascading impacts on financial markets and could force companies to increase insurance premiums, reducing insurance affordability and shifting more of the burden of disaster-related losses on governments and individuals10.

Recent work has started to build an understanding of the physical mechanisms that connect the occurrence of extremes across different regions. Kornhuber et al.17 found that the co-occurring summer 2018 heatwaves across North America, Western Europe, and the Caspian Sea region were driven by a recurrent wave-7 circulation pattern in the Northern-hemisphere mid-latitude jet stream. More generally, the occurrence of Rossby wave numbers 5 and 7 are found to substantially increase the probability of spatially compounding heat extremes over multiple mid-latitude regions including Central North America, Eastern Europe, and Eastern Asia, reducing global average crop production by nearly 4%18. The occurrence of Rossby waves can also link extreme events in the mid-latitudes and subtropics. For instance, Lau and Kim19 identified the role of Rossby wave trains in linking two record-setting extreme events during summer 2010—the persistent Russian heat wave and catastrophic flooding in Pakistan—with land-atmosphere feedbacks amplifying the Russian heat wave and moisture transport from the Bay of Bengal sustaining and amplifying the rains over Pakistan. Such compound extremes simultaneously affected millions of people and triggered a global food price spike associated with an approximately 30% loss in grain production in Russia20, which is a leading contributor to the global wheat trade21.

While recent studies of compound extremes have focused on the Northern Hemisphere mid-latitudes, the processes influencing compound extremes across the lower latitudes have received relatively little attention. Singh et al.22 investigated the underlying mechanisms of one such event—compound severe droughts across South Asia, East Asia, Brazil, and North and South Africa during 1876–1878, which were linked to the famines that contributed to the Late Victorian Holocausts23. The severity, duration, and extent of this compound drought event was shaped by the co-occurrence of a record-breaking El Niño (1877–1878), a record strong Indian Ocean Dipole (IOD) (1877), and record warm conditions in the North Atlantic Ocean (1878)22. El Niño Southern Oscillation (ENSO) is one of the main modes of variability that can cause simultaneous droughts and consequently affect food production in multiple remote regions. For instance, the reduction in global maize production in 1983 resulting from simultaneous crop failures across multiple regions13 is linked to the strong 1982–1983 El Niño event24. ENSO teleconnections lead to correlated climate risks between agricultural regions in North and South America and across the Pacific in Northern China and Australia25. For example, maize and soybean growing conditions in the US and southeast South America are favorable during the El-Niño phase, while the conditions are unfavorable in northern China, Brazil, and Southern Mexico25. In addition to ENSO, modes of variability in the Indian and Atlantic Ocean such as the Indian Ocean Dipole (IOD), tropical Atlantic variability, and the North Atlantic Oscillation are found to substantially affect the production of globally-aggregated maize, soybean, and wheat24. The influence of the interaction between these modes of natural variability on spatially compounding droughts across various regions has not yet been investigated.

Here, we examine the influence of four modes of natural climate variability on compound droughts across ten regions (Fig. 1a) defined in the SREX2 - Amazon (AMZ), Central America (CAM), Central North America (CNA), East Africa (EAF), East Asia (EAS), East North America (ENA), South Asia (SAS), Southeast Asia (SEA), Tibetan Plateau (TIB), and West Africa (WAF). We select these regions for three main reasons: (1) these regions include areas that receive a majority of their annual precipitation during the summer season (June–September) and experience high monthly precipitation variability, (2) several of these regions are physically connected by the global summer monsoon system26,27, and (3) climate variability across these regions are affected by similar modes of sea surface temperature (SST) variability. Our analysis only focuses on areas within these regions that meet the criteria of predominantly summer season precipitation and high monthly variability, which are identified based on the Shannon Entropy Index. These regions include major population centers with high levels of poverty and food insecurity and a number of major grains producing regions of the world, making them important in the context of global food security.

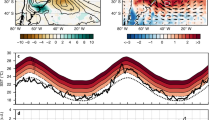
Fig. 1: Historical characteristics of compound drought events.
figure 1

a Map showing the ten SREX regions (red line) and the ocean regions (blue dashed lines) used to define various modes of variability considered in this study. Red text indicates the fraction of each SREX region with high entropy values [entropy > 4.86, which is the median entropy value across ten SREX regions] (teal color). b Historical timeseries of the number of regions experiencing summer season (June–September) drought (gray) and the total drought affected area (green) based on the Climate Hazards Group InfraRed Precipitation with Station (CHIRPS) precipitation data (1981–2018). The gray dashed line indicates the threshold of the number of regions used to define a compound drought event. Gray shading indicates the years with compound droughts. c Drought affected area in each season over each SREX region. Blue circles indicate seasons when the drought-affected area exceeds 80th percentile of the long-term average drought area. The magnitude of the 80th percentile thresholds for drought area are indicated on the right beside each region.

Full size image

The predominant influence of tropical Pacific SSTs (El-Niño or La-Nina condition) on precipitation variability over these regions is well-known28,29. In addition, previous studies have highlighted the significant influence of other modes of variability such as the IOD, the Atlantic Niño and the Tropical North Atlantic (TNA) alongside El-Niño on individual regions such as SAS30,31, WAF/EAF32,33, EAS34,35, SEA36, and AMZ37,38. We aim to understand how the co-occurrence of these modes of variability influence the characteristics of spatially compound droughts across the ten SREX regions. By advancing the knowledge of the physical drivers of compound droughts, the findings from this study have relevance for quantifying the cascading risk to critical, globally connected socio-economic sectors such as agriculture and thereby to regional and global food security and disaster risk management. By identifying SST conditions that have prediction skill on seasonal timescales39,40,41, our findings also highlight the potential for predictability of such events that can aid in predicting and managing their impacts42.

Results and discussion

Compound drought characteristics and their physical drivers

To identify summer season (June–September) compound droughts across the ten SREX regions (Fig. 1a), we utilize the Standardized Precipitation Index (SPI), which is a commonly-used measure of meteorological drought. Our analysis is limited to grid cells within each region that have high entropy values (Fig. 1a), signifying substantial summer season precipitation and high monthly precipitation variability. We define drought at a grid cell when SPI is below −1 standard deviation (< −1σ) and consider a region under drought when total number of grids with SPI < −1σ exceeds 80th percentile of the historical drought area for that region (see “Methods” section; Fig. 1c). Based on these definitions, we find 11 years since 1981 that have at least three regions simultaneously experiencing droughts (Fig. 1b), which we hereafter refer to as compound droughts.

El Niño exhibits the strongest influence on the occurrences of compound droughts in the observations. 8 of the 11 observed compound droughts in CHIRPS are associated with anomalously warm SSTs in the Niño3.4 region, with seven of them classified as El Niño events (≥0.5σ; Fig. 2). A majority of compound droughts occur during the developing phase of moderate to strong El Niño (SST anomaly >1σ) (Fig. S1) and only two compound droughts are associated with anomalously cold SST over Niño3.4 region. For instance, the strong El Niños of 1982, 1997, and 2015 resulted in widespread and severe compound droughts that simultaneously affected over five of the study regions. In each case, the total drought affected area across all ten regions exceeded the historical 90th percentile (referred to as widespread droughts) and average SPI across all regions remained in the lowest historical 10th percentile (referred to as severe droughts; Fig. 2). However, not all strong El Niño years led to compound droughts (e.g., 1987) and substantial SST anomalies across the Atlantic and Indian Ocean basins were also present during the 11 compound droughts (Fig. S2), indicating the possibility of a more complex interplay of multiple modes of ocean variability. Therefore, we seek to investigate the influence of individual and co-occurring natural modes of ocean variability on the characteristics of compound droughts. Specifically, we consider El Niño co-occurrences with IOD, Atlantic Niño, and TNA, since their influences on the interannual precipitation variability in our study regions are well established30,43. We note that 7 of 12 positive IOD (IOD+; DMI > 0.5σ), 5 of 11 negative Atlantic Niño (AtlNiño−; SST anomaly < −0.5σ), and 7 of 14 negative TNA (TNA−; SST anomaly < −0.5σ) co-occurred with compound droughts (Fig. 2). Overall, more than 60% (7 out of 11) of the observed compound droughts occurred during the years when two or more of these modes of ocean variability were active (Fig. 2).

Fig. 2: Drought characteristics and variability modes.
figure 2

Top three rows show the drought characteristics from CHIRPS and bottom four rows show the four SST indices from National Oceanic and Atmospheric Administration (NOAA) Optimum Interpolation (OI) SST dataset version 2 (V2) in each year (1981–2018). The white dots indicate years with severe droughts (row 1), widespread droughts (row 2) and compound droughts (row 3). White dots in the bottom four rows indicate years with positive SST anomalies (≥0.5σ) over Niño3.4 and IOD regions and negative (≤−0.5σ) SST anomalies over TNA and AtlNiño regions.

Full size image

The apparent dominance of El Niño as a major player during the episodes of compound droughts is not sensitive to the choice of threshold used to define drought. For instance, if classification of a region under drought is based on 90th percentile of the historical drought area for that region instead of the 80th percentile, the total number of compound droughts in the last four decades expectedly reduces (5 instead of 11) (Fig. S1), however, 80% of them are still during strong El Niño events. These findings are also insensitive to the choice of the observational dataset. For instance, use of precipitation from Climate Research Unit (CRU) and SSTs from Extended Reconstructed Sea Surface Temperature (ERSST) NOAA V544 over 1901–2018 yields nearly 70% (12 of the 17) of compound and widespread droughts during strong El Niño events (Fig. S3). Similar to CHIRPS, more than half (~60%) of the compound droughts are associated with the co-occurrence of two or more modes of ocean variability (Fig. S3). While we do find 8 of the 39 compound droughts in the 118-year record associated with opposite phases of two or more of these variability modes (Figs. 2 and S3), those conditions are comparatively rare45.

Identifying relevant phases of natural variability modes

To establish the relationship between these modes of ocean variability and SPI in the study regions, we perform a multiple linear regression analysis (Fig. S4). Our analyses reveal a widespread and consistent negative influence of the Niño3.4 SST anomalies (Fig. S4a) and positive influence of the Atlantic Niño SST anomalies (Fig. S4b) on SPI in most regions, suggesting that Niño3.4+ and AtlNiño− conditions are conducive to droughts in these regions. In contrast, we find that the TNA SST anomalies (Fig. S4c) and the IOD (Fig. S4d) have a varied influence across these regions. For instance, the IOD has a positive influence on SPI over parts of WAF, EAF and SAS but a negative influence over parts of CNA and SEA. This indicates that IOD+ conditions promote droughts over CNA and SEA. Similarly, the TNA SST anomalies exhibit a negative influence over parts of AMZ, but positive influence over parts of CAM, SEA, and WAF, which suggest that TNA− conditions favor droughts over the latter regions.

We also calculate the fraction of the total drought events in each region during different phases of these modes of ocean variability (Fig. S5). Positive Niño3.4 SST anomalies (>0.5σ; Niño3.4+) are linked to a substantial fraction of historical drought events over several regions. Niño3.4+ (nine events historically) conditions are associated with ≥75% of droughts over CAM, SAS, and SEA, and ≥50% of droughts over EAF, WAF, and TIB. Similarly, TNA− conditions are coincident with ≥75% of droughts over CAM and SAS, and ≥50% over SEA, TIB, and WAF. AtlNiño- events coincide with ≥50% of droughts over AMZ, EAS, and WAF while IOD+ is present during ≥75% of droughts over SEA and ≥50% of droughts over AMZ, CAM, CAN, SAS, TIB, and WAF (Fig. S5). In contrast, the opposite phases of IOD, TNA, and AtlNiño are associated with a small fraction of droughts over only one region. Collectively, these results suggest the predominant influence of Niño3.4+, IOD+, TNA−, and AtlNiño− on individual regions and compound droughts. These conditions are also more likely to co-occur. For instance, El Niño conditions are more likely to co-occur with IOD+ conditions as they tend to drive warmer SSTs over the western Indian ocean through the atmospheric bridge and cooler SSTs over the eastern Indian ocean via oceanic Indonesian throughflow45. Similarly, cold SSTs over the tropical north Atlantic Ocean can induce warm conditions over the Pacific Ocean by influencing the Walker circulations45, making cold TNA conditions and El Niños more likely. Therefore, we further explore how IOD+, TNA−, and AtlNiño− modes interact with El Niño to influence drought characteristics over individual regions and consequently, compound droughts.

Amplifying effect of co-occurring modes with El Niño

The interplay of Niño3.4+ with other modes of ocean variability requires several instances of their co-occurrences for robustly distinguishing their individual and combined influence. Given the limited length of the observed record, we primarily study their interactions in a multicentury (1800 years) preindustrial climate simulation from the National Center for Atmospheric Research (NCAR) Community Earth System Model (CESM)46. CESM skillfully represents precipitation over the study regions and SST variability representing various oceanic modes relevant to this study47,48. We have included comparisons of CESM with observations, where feasible (Fig. 3). The 1800-year preindustrial simulation provides a substantially larger number of events to examine the relative and combined influence of natural modes of variability without any changes resulting from external climate forcing (Fig. 3). We compare regional drought characteristics during three types of conditions (see “Methods” section)—(1) El Niño co-occurring with other modes (either IOD+ or/and TNA− or/and AtlNiño−; referred to as co-occurring conditions), (2) El Niño occurring alone (referred to as Niño3.4+ conditions), and (3) neutral conditions, when none of them are active (Fig. 3). It should be noted that there are no neutral conditions in the 38-year observational record, and limited instances of the other two conditions does not allow their robust comparisons (e.g., there are 2 Niño3.4+ and 7 co-occurring conditions).

Fig. 3: Influence of El Niño and co-occurring modes of variability on regional drought characteristics.
figure 3

Observed (1981–2018; filled circles) and simulated (boxplots and unfilled circles) distribution of a drought area and b drought intensity in each SREX region during neutral (gray), Niño3.4+ (green) and co-occurring (orange) conditions. Neutral conditions represent summer (June–September) seasons with neutral phases (< ± 0.5 σ) of the four modes of variability considered. Niño3.4+ conditions represent seasons with SST anomalies >0.5σ over the Niño3.4 region only and other modes in their neutral phases. Co-occurring conditions include summer seasons with Niño3.4+ conditions co-occur with either cold Atlantic Niño SST anomalies (<−0.5σ), cold TNA SST anomalies (<−0.5σ) or positive IOD (DMI >0.5σ) conditions, consistent with the phases of these modes that are associated with droughts in most regions. Gray arrows indicate significant differences in the mean of distribution of drought area and intensity during Niño3.4+ or co-occurring conditions relative to neutral conditions at 5% significance level. Green arrows indicate significant differences in the mean of distributions between Niño3.4+ and co-occurring conditions at 5% significance level. Black dots show the mean of the distribution in each boxplot. Significance of the difference in the drought characteristics between Niño3.4+ and co-occurring conditions in observations is not estimated due to small sample sizes. There are 2 Niño3.4+ and 7 co-occurring conditions in observations and 27 Niño3.4+ and 426 co-occurring conditions in the CESM pre-industrial simulation.

Full size image

During Niño3.4+, a large fraction of all tropical regions—AMZ, CAM, EAF, WAF, SAS, and SEA—experience abnormally dry anomalies (Fig. S6), consistent with well-known observed ENSO teleconnections49,50,51. The co-occurrence of Niño3.4+ with other modes intensifies dry conditions over EAS, SEA, CAM, and AMZ, while the opposite impact is experienced over EAF (Fig. S6). The simulated composites show consistency with both observed datasets over most regions, with the exception of biases in the extent and intensity of precipitation deficits over parts of SAS, WAF and EAF between model and observations (Fig. S6). We also quantify the aggregate drought area and intensity across the individual regions (Fig. 3). In the CESM preindustrial simulation, two regions—CAM and SEA—experience significantly larger drought areas during both Niño3.4+ and co-occurring conditions relative to neutral conditions (indicated by gray arrows in Fig. 3a), while two regions—AMZ and SAS only show significantly larger droughts during co-occurring conditions but not during Niño3.4+ relative to neutral conditions (box plots, Fig. 3a). In addition, co-occurring conditions expand the drought area over AMZ and SEA and significantly reduce drought area over EAF relative to Niño3.4+ (indicated by green arrows in Fig. 3a), consistent with observations (solid circles, Fig. 3a), highlighting their role in shaping drought characteristics. Moreover, Niño3.4+ significantly increases drought intensity over EAF, SEA, and WAF relative to neutral conditions. Further, co-occurring conditions are associated with significantly higher drought intensity over AMZ, CAM, WAF, EAF, SAS, and SEA relative to Niño3.4+ (Fig. 3b), consistent with observations (solid circles, Fig. 3b). Overall, these findings highlight the complex interplay of Niño3.4+ and other modes of ocean variability that control the spatial footprint and severity of over studies regions (Figs. 3 and S6).

While Niño3.4+ exhibits the strongest influence on regional precipitation characteristics, (Fig. 3 and S6), the frequency, severity and spatial extent of compound droughts is substantially enhanced when Niño3.4+ co-occurs with other natural modes of ocean variability (Fig. S7). For instance, the probability of compound droughts in CESM increases from 0.09 during neutral conditions to ~0.27 during Niño3.4+ conditions and ~0.43 during co-occurring conditions (Fig. S7d). Likewise, the probability of widespread and severe droughts is nearly 70% higher during co-occurring conditions relative to Niño3.4+ conditions alone (Fig. S7e, f). These model-based findings are mostly consistent with observations (Fig. S7a–c), except that the simulated number of drought-affected regions during co-occurring conditions is not significantly higher even though the probability of simulated compound droughts is ~20% higher relative to Niño3.4+ conditions in observations (Fig. S7a).

Influence of co-occurring modes on regional droughts

Next, we isolate the influence of each individual mode of variability and their co-occurrence with Niño3.4+ on precipitation characteristics (Fig. 4). AtlNiño− is associated with anomalously dry conditions (relative to neutral) over WAF, central AMZ, northern TIB and EAS (Fig. 4a, b). Its co-occurrence with Niño3.4+ significantly influences precipitation anomalies in the Atlantic Rim regions, including stronger precipitation deficits over WAF and the AMZ and reversal of Niño3.4+ forced anomalies (wet to dry) over CNA (Fig. 4e, f). More intense and widespread drying over WAF and AMZ during Niño3.4+/AtlNiño− occurs without substantial increase in SST anomalies over the Niño3.4 region, which indicates an additive influence of these modes on regional drought characteristics. Likewise, co-occurring TNA-/Niño3.4+ conditions also appear to have an additive influence though the composites do indicate significantly higher SST anomalies over the part of Niño3.4 region indicative of slightly stronger Niño3.4+ conditions (Fig. 4g). Individually, TNA− are associated with dry conditions over WAF, EAF, CAM, southern SAS, and northern TIB relative to neutral conditions (Fig. 4a, c, e). Co-occurring TNA−/Niño3.4+ conditions amplify the Niño3.4+-related drying over CAM, AMZ, EAF, northern TIB, central EAS, and SEA. In addition, there are more widespread precipitation deficits across WAF, EAF and SAS over areas that would experience wet anomalies during Niño3.4+ (Fig. 4, e, g).

Fig. 4: Simulated influence of individual variability modes and co-occurring conditions.
figure 4

Composites of precipitation and SST anomalies during a neutral conditions, b AtlNiño− conditions only, c TNA− conditions only, d IOD+ conditions only, e Niño3.4+ conditions only, and co-occurring f Niño3.4+/AtlNiño−, g Niño3.4+/TNA−, and h Niño3.4+/IOD+ conditions. Numbers in the headings indicate the number of summer seasons with individual and co-occurring phases of the modes used in each composite. Co-occurring conditions indicated by Niño3.4+/IOD+, Niño3.4+/AtlNiño−, and Niño3.4+/TNA− denote co-occurrences of specific modes while other modes are in their neutral phases. The hatched SST and precipitation composites on the left indicate significant differences in the composite mean relative to neutral conditions and on the right indicate significant differences in the composite mean relative to Niño3.4+ conditions, at 5% significance level.

Full size image

In contrast to the relatively consistent drying influence of these modes across multiple regions, IOD+ exhibits a dipolar influence across the regions surrounding the Indian Ocean. IOD+ is associated with anomalous drying over western SEA, northern SAS, TIB, northeast EAS and parts of CNA and anomalous wet conditions over EAF52 and WAF49 (Fig. 4a, d). Therefore, Niño3.4+/IOD+ co-occurrence dampens the drying impacts of Niño3.4+across the latter regions, while it expands and intensifies precipitation deficits over SAS and SEA. These findings are consistent with Preethi et al.49 suggesting the co-occurrence of IOD+ conditions can dampen the influence of tropical drivers over Africa. One confounding factor in determining the modulating influence of the IOD+ on Niño3.4+-related drought effects is that intensity of Niño3.4+ is substantially higher during IOD+ (Fig. 4e, h), as studies suggest that strong Niño3.4+ events force IOD+ conditions53,54,55, which is perhaps partly responsible for the intensification of drought severity over SEA and parts of SAS during Niño3.4+/IOD+ co-occurrence.

Given the substantial effect of all four natural variability modes on regional precipitation (Figs. 3 and 4), we assess the individual and combined influence of each of the combinations on aggregate drought area and intensity across a subset of six SREX regions that are substantially affected by these variability modes (Fig. 5). Amongst the four modes, Niño3.4+ significantly increases drought area over the largest number of these regions—CAM, EAF, and SEA-relative to neutral conditions, followed by TNA- that increases drought area over CAM and EAF (indicated by gray arrows in Fig. 5a). The individual influence of other modes is limited to fewer regions—AtlNiño− significantly increases drought area over WAF, whereas IOD+ significantly decreases drought area over EAF and WAF and increases it over SAS. However, their co-occurrence with Niño3.4+ has significant effects over multiple regions. Co-occurring Niño3.4+/TNA− are associated with significantly higher drought area over all regions but AMZ relative to neutral conditions (gray arrows in Fig. 5a). In addition, the co-occurring Niño3.4+/TNA− significantly (at 5% significance level) increase drought area over SEA and CAM while Niño3.4+/IOD+ co-occurrence significantly decreases drought area over EAF and increases drought area over SEA, relative to Niño3.4+ alone (indicated by green arrows in Fig. 5a). AMZ, which experiences no significant change in drought area under Niño3.4+ relative to neutral conditions, has a significantly higher drought area when Niño3.4+/AtlNiño− or Niño3.4+/IOD+ co-occur. Similarly, WAF only shows significantly higher drought area during co-occurring Niño3.4+/TNA− and Niño3.4+/AtlNiño− but not during Niño3.4+ alone.

Fig. 5: Influence of individual and co-occurring modes of variability on regional drought characteristics.
figure 5

Box plots represent the distribution of a drought area and b drought intensity across a subset of SREX regions with the largest effects of natural variability modes during seasons with neutral conditions, individual occurrences of natural variability modes (AtlNiño, TNA−, IOD+, and Niño3.4+), and co-occurring conditions (Niño3.4+/IOD+, Niño3.4+/AtlNiño-, and Niño3.4+/TNA), noted above each boxplot, from the CESM preindustrial simulation. Here, we show a subset of six SREX regions which are significantly affected by these modes of natural variability. Gray arrows indicate significant differences in the mean of distribution of drought area and intensity corresponding to various conditions relative to neutral conditions at 5% significance level. Green arrows indicate significant differences in the mean of distributions between co-occurring and Niño3.4+ conditions at 5% significance level. Black dots show the mean of the distribution in each boxplot.

Full size image

Unlike the influence on drought area, we find a more limited influence of the individual occurrences of these modes on drought intensity over most regions, except an increase in drought intensity over WAF during TNA− and AtlNiño− and over EAF, SEA, and WAF during Niño3.4+ relative to neutral conditions (indicated by gray arrows in Fig. 5b). However, co-occurring modes significantly increase drought intensity over all six regions relative to neutral conditions. For instance, despite no substantial difference in drought intensity over CAM and SAS between Niño3.4+ and neutral conditions, co-occurring Niño3.4+/TNA− lead to significantly higher drought intensity over these regions and over SEA and WAF (indicated by gray arrows in Fig. 5a). In addition, co-occurring Niño3.4+/IOD+ are associated with significantly higher drought intensity over SEA and SAS and Niño3.4+/TNA− are associated with significantly higher drought intensity over CAM and SAS, relative to Niño3.4+ alone (indicated by green arrows in Fig. 5b).

Influence of co-occurring modes on compound droughts

The individual and co-occurring influences of these modes on regional drought characteristic also leads to the episodes of compound droughts across ten SREX regions when at least three regions simultaneously experience drought during the same season (Fig. 6). The probability of experiencing compound droughts increases approximately threefold during AtlNiño- (probability = 0.25), TNA− (probability = 0.24) and Niño3.4+ (probability = 0.27) relative to neutral conditions (probability = 0.09) (gray arrows in Fig. 6a), which is further amplified during their co-occurrences. For instance, co-occurring Niño3.4+/IOD+ or Niño3.4+/AtlNiño− increase the probability of compound droughts by a factor of ~5 while co-occurring TNA-/ Niño3.4+ increase it by a factor of ~7 relative to neutral conditions. Overall, the co-occurring Niño3.4+/TNA− conditions are associated with the largest amplification of compound drought risk (~2.5 or ~150%) over their probability during Niño3.4+ conditions.

Fig. 6: Influence of modes of variability on compound drought characteristics.
figure 6

The distribution of a number of regions under drought, b drought area, and c drought intensity during seasons with individually occurring variability modes and co-occurring conditions noted below each boxplot, from the CESM preindustrial simulation. Horizontal gray solid lines indicate the thresholds used to define a compound (i.e., \(\ge\) three regions under drought, gray line), b widespread (i.e., events with >90th percentile of total area (~21%) across all ten regions concurrently affected by drought, gray line), and c severe (i.e., average SPI across all drought affected areas < 10th percentile (~−1.52), gray line) droughts. Text above the boxplots in a indicates the probability of compound droughts under each condition, b indicates the probability of experiencing widespread droughts and c indicates the probability of experiencing intense droughts. For example, the probability of three or more regions concurrently affected by droughts under neutral and Niño3.4+ conditions is 0.1 and 0.41, respectively. Gray arrows indicate significant differences in the distribution of drought area and intensity corresponding to various conditions relative to neutral conditions at 5% significance level. Green arrows indicate significant differences in the distributions between the co-occurring conditions and Niño3.4+ conditions at 5% significance level. Black dots show the mean of the distribution in each boxplot.

Full size image

Similarly, the total compound drought area measured across all ten SREX regions shows a significant increase during TNA- and Niño3.4+ relative to neutral conditions (Fig. 6b). Niño3.4+ increases the probability of widespread droughts, events with drought area in the top 90th percentile (~21%), to 0.19 compared to ~0 during neutral conditions. Co-occurrence of other natural variability modes with Niño3.4+ also substantially increase compound drought area compared to neutral conditions. Most notably, co-occurring TNA−/Niño3.4+ raises the probability of widespread droughts by a factor of ~3 relative to Niño3.4+. Likewise, co-occurrence of various ocean variability modes amplifies the probability of severe compound droughts events with the area-weighted average drought intensity across all regions in the lowest 10th percentile (~−1.52) (Fig. 6c). Co-occurring Niño3.4+/TNA− are associated with a 2.5 times higher probability of severe droughts relative to Niño3.4+. The co-occurring Niño3.4+/IOD+ and Niño3.4+/AtlNiño- also increase the probability of severe droughts by a factor of ~2 and ~1.5, respectively relative to Niño3.4+. Overall, these analyses suggest that Niño3.4+ leads to the largest increase in the probability, extent and intensity of compound droughts relative to the neutral conditions, and the co-occurrence of IOD+, and/or TNA−, and/or AtlNiño- with Niño3.4+ can significantly amplify these characteristics through their influence on drought intensity and extent over one or multiple SREX regions.

Physical mechanisms associated with compound droughts

We investigate the underlying physical mechanisms that connect simultaneous precipitation anomalies over several terrestrial regions with SST anomalies in various oceanic basins by analyzing upper level (200 hPa) velocity potential (VP) and low-level (at 850 hPa) moisture flux convergence (MFC) anomalies corresponding to the individual and co-occurring modes (Fig. 7). The VP describes large-scale horizontal convergence and divergence centers of the atmospheric circulation and is particularly useful in identifying anomalies in the tropical circulations. It is well known that El Niño modulates tropical/sub-tropical precipitation via forcing anomalies in the Walker circulation56,57. Climatologically, the strongest upper-level divergence centers (also known as the ascending branches of the Walker circulation) during the boreal summer are located in the western Pacific and eastern Indian Oceans and their subsiding branches are located in the eastern Pacific, southwestern Indian, and Atlantic Oceans (Fig. S8). These upper-level divergence centers coincide with the strong monsoon-driven convection across Asia. During Niño3.4+, the ascending (subsiding) branches of the Walker circulation in the western Pacific and eastern Indian (eastern Pacific and south Atlantic) weaken, leading to anomalous upper level convergence (divergence) anomalies that are reflected in the positive (negative) VP anomalies (Fig. 7a). Such changes in the tropical circulations weaken boreal summer monsoons, reduce low-level moisture convergence and consequently, support drier conditions over those regions (Fig. 7a, e). The associated anomalies in the South Atlantic high also induce changes in the trade winds over the equatorial Atlantic which influence moisture supply over AMZ, CAM, and WAF (Fig. 7e).

Fig. 7: Mechanism of compound droughts associated with co-occurring modes.
figure 7

Composite anomalies of a upper-level (200 hPa) velocity potential (VP) and e lower-level (850 hPa) moisture flux convergence (MFC) during Niño3.4+ conditions. Shading indicates the moisture flux convergence and arrows indicate winds. Differences of the VP and MFC composites associated with co-occurring b, f Niño3.4+/Atl Niño−, c, g Niño3.4+/TNA−, and d, h Niño3.4+/IOD+ conditions relative to Niño3.4+ conditions.

Full size image

The co-occurrence of AtlNiño− with Niño3.4+ noticeably amplifies the positive VP anomalies over WAF during Niño3.4+ and reduces the anomalous ascent of the Walker circulation over CAM and AMZ, (Figs. 5a and 7f). These circulation changes along with cooler than normal SSTs in the region lead to reduced moisture convergence, expanding the precipitation deficits over these regions relative to during Niño3.4+ (Figs. 4e, f and 7e, f). Co-occurring Niño3.4+/TNA− exhibit the strongest and most widespread positive VP anomalies over the studied regions that influence the large-scale monsoon circulations (Fig. 7a, c) and low-level moisture availability (Fig. 7e, g), which further intensify the strength of Niño3.4+-induced drying as reflected in Figs. 4g and 5b. Earlier studies also note that TNA− influences precipitation over the African regions by altering the northward extent of the West African Monsoon49 and moisture transport from the Atlantic Ocean and Gulf of Guinea58, and over CAM through the modulation of low-level moisture convergence over the Caribbean region and the strength of the Atlantic northeasterly trades59. The main influence of IOD+ is seen over the African and Asian regions. IOD+ reduces (strengthens) the influence of Niño3.4+ on the upper-level circulation over Africa (EAS and SEA), which reduces (intensifies) the extent and intensity of dry anomalies (Fig. 5a, b). Our findings are consistent with previous studies that have found that IOD+ weakens the African Easterly Jet and strengthens the Tropical Easterly Jet, while Niño3.4+ generally drives the opposite response49. Similarly, the anomalously cool SSTs surrounding SEA during IOD+ contribute to reducing the low-level moisture convergence (Fig. 7e, h), and thereby amplify the regional drying associated with substantial weakening of Walker circulation60. Overall, we note that the simultaneous occurrence of other modes of ocean variability oftentimes intensifies and/or expands the large-scale circulation anomalies associated with Niño3.4+, resulting in more intense or widespread moisture deficits over several regions.

Summary and conclusions

Spatially compound extremes impose amplifying pressures on the disaster risk management resources and the global food system. As the impacts of such extremes are increasingly being recognized, recent studies have started to investigate their probability of occurrence and associated mechanisms7,12,14,18,24. While previous studies have focused on the mechanisms of compound temperature extremes across the mid-latitudes18, we examine the drivers of compound droughts across ten SREX regions that predominantly experience summer precipitation with high variability, identified based on the Shannon Entropy index. We use the 38-year observational record and an 1800-year CESM preindustrial climate simulation to examine the characteristics of compound droughts and the influence of natural ocean variability modes. We identify 11 historical compound droughts in the observational records, of which seven are associated with strong El Niño conditions. In addition to the central role of El Niño in driving these events, our analysis based on observational and the preindustrial simulation demonstrates substantial influence of three other modes of ocean variability—IOD, TNA, and AtlNiño conditions—that amplify various characteristics of regional droughts and global occurrences of compound droughts.

El Niño leads to a significant increase in the drought area and intensity over the largest number of regions relative to the other modes of natural variability (Figs. 3 and 5), and in turn, increase the probability of compound droughts by a factor of ~3, compared to their probability during neutral conditions (Fig. 6). Additionally, El Niño heightens the probability of widespread and severe droughts to 0.19 and 0.17, respectively, relative to 0 during neutral conditions. Other modes of natural variability show a varying influence on drought extent and intensity over specific regions and therefore, by themselves have an overall smaller impact on the probability of compound droughts compared to the impact of El Niño. The TNA mode has the largest influence among the three other modes, with TNA− significantly amplifies drought area across CAM and SEA, and drought intensity over CAM and SAS during its co-occurrence with El Niño, contributing to a 2.5-fold, 3-fold, and 2.5-fold increase in probability of compound, widespread and severe droughts, respectively (Fig. 6). In contrast, because IOD+ dampens the influence of El Niño on drought area in EAF but amplifies it in SEA, and its co-occurrence with Niño3.4+ leads to a relatively moderate 1.6-fold increase in the probability of compound, widespread, and severe droughts (Fig. 6).

Overall, our analyses reveal the importance of considering other modes of ocean variability in addition to El Niño for assessing the risk, extent, and severity of compound droughts. We highlight a few caveats and limitations of this study. First, because of the relatively small sample size of the precipitation record in several of the study regions, our analysis of the individual and combined influence of natural variability modes largely depends on the long preindustrial climate simulation. Second, although the CESM simulation largely captures the relationship between various modes of variability considered in this study, it demonstrates stronger than observed correlations between TNA and ENSO, and IOD and ENSO at different lead times. Third, while we utilize the CESM model, which is one of the most skillful climate models in representing El Niño conditions48, we do not investigate intermodel differences in the identified relationships that may arise due to varying representations of precipitation processes, natural variability characteristics and teleconnections. Four, we do not consider the potential lead-lag relationships between some of these modes of variability and their regional impacts on precipitation45,61,62,63. Efforts to comprehensively assess these relationships and interactions between modes on various timescales can support predictability efforts. In addition, our future work will also focus on investigating the physical processes underlying the interactions between these modes and the regional and global impacts of their co-occurrence.

Compound droughts have the potential to induce synchronous crop failures and simultaneously cause other impacts across various societal sectors in multiple regions, leading to cascading global consequences. In the backdrop of the global interconnectivity of our socio-economic and physical systems, our study highlights the importance of considering the occurrence of and interactions between multiple modes of natural variability that represent the large-scale state of climate in characterizing the compound drought risks and their impacts on global food security, rather than solely focusing on individual modes that drive region-specific droughts. Our study presents the first step towards understanding the factors that influence compound droughts and their characteristics, which can help understand how they might change in response to the projected increases in extreme El Niño conditions47 and positive IOD conditions64. Understanding the factors that shape the characteristics of compound droughts have important implications for enhancing society’s resilience to the multitude impacts of droughts including food insecurity and water scarcity. A better understanding of compound drought risks is relevant for informing agriculture insurance companies to design more optimal crop insurance schemes, which are presently based on the historical probabilities of extreme events in individual regions without considering their spatial relationships. By identifying how interactions among different modes of natural variability can influence compound droughts, our study highlights the potential for seasonal prediction of such events to aid in the management of their impacts. Several modes of SST variability have skillful predictions at varying lead times including up to 9-months for El Niño39, up to 6 months for the IOD40 and 4 months for tropical Atlantic Ocean SSTs41. Timely predictions of droughts and drought-induced shocks in agricultural production will help manage potential food insecurity in several vulnerable regions42. Additionally, predictions of such events have implications for international trade, where the agribusiness industry and grain producers can get enough time to minimize the economic losses due to anticipated disasters.

Methods

Data

We primarily use precipitation from the widely-used high-resolution (0.25° × 0.25°) Climate Hazards group Infrared Precipitation with Stations (CHIRPS version 2) dataset (1981 to present). The CHIRPS daily precipitation dataset has been used for the assessment of daily, monthly, seasonal, and annual precipitation characteristics in several regions of the world65,66,67,68. CHIRPS blends satellite-based precipitation estimates with in situ observations, and models of terrain-based precipitation modification to provide high resolution, spatially-complete, and continuous long-term data from 1981 to present, providing distinct advantages over rain-gauge-based products that include variations in station density or remotely sensed data that have a limited temporal extent69,70.

In order to establish the robustness of our findings, we also compare our analyses with data from the Climate Prediction Center (CPC; 0.5° × 0.5°) and Climatic Research Unit (CRU; 0.5° × 0.5°), by comparing the Standardized Precipitation Index (SPI) across all ten SREX regions from all three datasets (Fig. S9). The SPI from CHIRPS and CRU are strongly correlated (\(\rho\) > 0.72) over all regions but CPC-based estimates exhibit comparatively lower correlations over some regions including EAF, WAF, SAS, and EAS. We find that CPC-based SPI does not capture documented droughts over AMZ71, SAS72 during the record breaking El Niño year 2015, and over SAS73, EAF74, and EAS75 in another well-known El Niño year 2009 (Fig. S9). Therefore, of these three datasets, we use CHIRPS for the remainder of our analysis. Further, while the Global Historical Climate Network has station-data availability over a longer period of time over some regions, we do not include it in this analysis due to the non-uniform density of stations across the study area, and temporal discontinuities in data availability. We obtain sea surface temperatures (SST) from the National Oceanic and Atmospheric Administration (NOAA) High Resolution (0.25° spatial resolution) Optimum Interpolation (OI) SST dataset version 2 (V2), which has temporal coverage from 1981 to present76. Although our observational analysis is based on precipitation from CHIRPS and SST from OI NOAA V2 due to their finer spatial resolution, we perform complementary analyses with the long-term observed precipitation from CRU77 (0.5° spatial resolution) and SSTs (2° spatial resolution) from Extended Reconstructed Sea Surface Temperature (ERSST) NOAA V544 during 1901–2018.

Given the limited length of the observed record, we further characterize the influence of various SST variability modes on precipitation variability in the ten SREX regions using an 1800-year preindustrial simulation from the CESM46. Since the simulation has constant preindustrial climate forcing, it isolates the influence of unforced natural climate variability from the confounding influence of changing external climate forcings46. We select the CESM model simulation because it is one of the most skillful modern climate models in reproducing El Niño behavior and its teleconnections47,48.

Selection of regions

We examine compound droughts across ten SREX regions4,9,78, which are selected based on the similarity in their precipitation characteristics. Specifically, we consider regions that show high variability in summer precipitation and receive a majority of their precipitation during the summer season. To identify the subregions that meet these criteria, we compute the Shannon Entropy Index for summer season precipitation, which is a concept drawn from information theory to measure the variability of a random variable79. The Shannon Entropy index is defined as measure of variability and has been used in hydroclimatic studies to assess the spatial and temporal variability of precipitation time series80. The Shannon entropy H can be computed as80,

$$H = - {\sum} {p_{\rm{i}}\log _2p_{\rm{i}}},$$
(1)

where p is the probability of each ith observation of the variable time series. We restrict our analyses to regions that have high entropy values over more than 30% of the total domain. Only ten tropical and mid-latitude SREX regions meet this criterion. Within these regions, we only consider areas with entropy values exceeding 4.86, which is the median entropy value across the regions considered.

Drought definitions

We define drought at each grid cell based on SPI calculated with accumulated summer season (June–September; JJAS) precipitation. Following the method developed by McKee et al.81, the probability of accumulated JJAS precipitation from all season is transformed to a standard normal distribution. The estimated JJAS SPI is similar to the JJAS precipitation anomaly, but the standardization makes it comparable across space and time. The SPI time series is linearly de-trended to eliminate long-term trends and capture interannual precipitation variability. We define a grid cell under drought if its SPI is less than –1 standard deviation (σ) of the long-term (1981–2018) mean SPI. We define a region under drought if the fractional area experiencing drought (SPI < −1σ) within that region exceeds the 80th percentile of the seasonal drought area distribution. We choose the 80th percentile threshold to define a region under drought because it captures several documented droughts across various regions and, compared to higher percentile thresholds, it is relatively less sensitive to the length of observational records. Additionally, higher percentiles (>80th percentile) also substantially limit the drought events sample size, limiting the statistical robustness of our findings. The drought extent is defined as the fraction of the area within a region with SPI < −1σ and the drought intensity is defined as the area weighted-average SPI value over all the grid cells experiencing drought. We define compound droughts as at least three of ten SREX regions simultaneously experiencing droughts. We define widespread drought as events in which the fraction of total area across all ten regions simultaneously affected by drought exceeds the 90th percentile of the long-term average drought area. We define severe drought as events in which average SPI across all drought affected areas falls below the 10th percentile of the long-term average SPI.

Multiple linear regression (MLR)

We perform a MLR analysis to understand the individual influence of Niño3.4, TNA, IOD, and Atlantic Niño indices on SPI across all SREX regions. Using MLR, we compute the regression coefficients (slope) between SPI (dependent variable) and these SST-based indices (independent variable). To examine the multicollinearity in this multiple regression model, we estimate the variation inflation factor (VIF) corresponding to each independent variable82. We found relatively low VIFs for all four indices (TNA—1.05; Atlantic Niño—1.17; Niño3.4—1.46; IOD—1.27), which suggests a minimal concern of multicollinearity in our regression model.

Natural variability modes

The Niño3.4 index is used to define ENSO as the average SST anomalies over 5°S–5°N, 170°–120°W83. The TNA index is estimated as the average SST anomalies over 5.5°–23.5°N, 15°–57.5°W84. The Atlantic Niño (AtlNiño) index is calculated from average SST anomalies over 5°S–5°N and 20°W–0°85, and IOD is identified by using the Dipole Mode Index (DMI), which is calculated as the SST difference between the western (50°–70°E, 10°S–10°N) and eastern (90°–110°E, 10°S– Equator) equatorial Indian Ocean22,86. The spatial extent of all regions used to calculate these indices are highlighted in Fig. 1. All indices are calculated for the summer. Niño3.4+ refers to El Niño conditions when JJAS positive SST anomaly over the Niño3.4 region is >0.5σ. TNA− and AtlNiño− refer to cold phases of these indices that are identified based on negative JJAS SST anomalies (< −0.5σ) over their corresponding regions. IOD+ refers to positive IOD when JJAS DMI is >0.5σ. Since, we aim to investigate the relationship between modes of ocean variability and compound droughts on interannual timescales, we remove the climate change signal by detrending the observed timeseries of all modes, SSTs and SPI, which makes the identified relationships more comparable between observations and preindustrial simulations.

To understand the influence of El-Niño and its interactions with other modes of natural variability on drought characteristics, we first categorize all available seasons in the observed record into Niño3.4+-only and co-occurring conditions. Niño3.4+-only conditions are defined as years when Niño3.4+ is active while all other modes are in their neutral phase (<±0.5). Co-occurring conditions are defined as years when Niño3.4+ co-occurs with AtlNiño−, TNA−, or IOD+ conditions. There are two Niño3.4+ and seven co-occurring conditions during the 38-year observed period. To get a larger distribution of compound droughts under various anomalous SST conditions, we examine these interactions in a 1800-year CESM preindustrial climate simulation.

In addition, we categorize years based on the individual occurrences of each variability mode, and their combined occurrences with Niño3.4+ to understand their individual and combined influence on drought characteristics relative to neutral conditions. Neutral conditions are defined as years without any substantial phase of either of the four modes of ocean variability. Niño3.4+/AtlNiño−, Niño3.4+/IOD+, and Niño3.4+/TNA− refer to years when Niño3.4+ co-occur with AtlNiño−, IOD+, and TNA−, respectively, while the other modes are in their neutral conditions.

We evaluate the lead correlations between each mode and JJAS SPI over study regions during 1901–2018 to assess the validity of using contemporaneous (JJAS) SSTs in each basin. Given that El Niño events typically peak in winter87, we examine correlations between the 4-month moving average of the Niño3.4 index starting from November of the previous year to September of the current year (Fig. S10). Although some regions show significant correlations at several month lag times, they constitute a relatively small fraction of the all regions considered (~12%) (Fig. S10a). The area with significant correlations between JJAS(0) (“0” refers to the months of the current year) SPI and ENSO increases substantially with reduced lead time of the ENSO index. Specifically, ~40% of the studied area shows the strongest correlation with instantaneous impact of summer ENSO conditions49,50,88,89,90 (Fig. S10a). In addition, JJAS(0) SPI shows the strongest correlation with contemporaneous ENSO (Fig. S10b). Similarly, we assess the correlations of JJAS(0) SPI with other modes of variability and find that the strongest and most widespread correlations across all regions altogether are with contemporaneous IOD and Atlantic Niño. The TNA index has its strongest correlations at a short lead time though the correlations are not substantially different than during the JJAS season (Fig. S10a, b).

We also note that there are some contemporaneous and lagged correlations between ENSO and other modes of variability61,62,63(Fig. S11). Consistent with previous studies, we find an insignificant contemporaneous correlation between co-occurring AtlNiño and ENSO62,63 but weak lead correlations up to 6 months in advance61. Further, we find insignificant correlations between TNA and ENSO on most timescales in observations. Correlations between IOD and ENSO are the strongest in JJAS (Fig. S11a). The simulations generally capture these relationships but indicate stronger than observed correlations between TNA and ENSO, and IOD and ENSO at nearly all lead times (Fig. S11b). These lagged correlations between modes61,62,63 highlight the potential for their predictability and their associated regional precipitation anomalies91 and warrant further investigation. However, our analyses are constrained to the influence of contemporaneous states of all modes on regional precipitation, given the overall strongest and most widespread influence of most modes on regional precipitation in these regions. Our choice of using contemporaneous SSTs follows numerous studies that have identified the importance of contemporaneous Pacific, Atlantic, and Indian Ocean SST conditions on monsoons, which govern precipitation over a majority of these regions49,50,92,93.

Statistical significance

We use the permutation test to assess the statistical significance of the differences in mean of drought characteristics during the occurrence of various combinations of natural ocean variability modes94. Permutation tests are becoming increasingly common to estimate the significance level of certain statistical analyses95. The non-parametric permutation test does not make any assumptions pertaining to sample size and distribution of the data, and is therefore suitable for a variety of situations, including for comparing distributions of different sizes, as is the case here. Here, we use the difference in the means of the two distributions as the test statistic. We first quantify the test statistic from the two original distributions and then randomly permute the samples from the two distributions, and re-estimate the test statistic from the resampled distributions. We repeat this procedure 10,000 times to obtain an empirical distribution of the test statistic, which represents the possible outcomes if the distributions were totally random. If the original test statistic is higher (lower) than the 95th (5th) percentile of the statistic from these permuted samples, we consider the mean of the distributions to be significantly different at the 5% level.