Abstract
Some of the largest and most persistent circulation errors in global numerical weather prediction and climate models are attributable to the inadequate representation of the impacts of orography on the atmospheric flow. Existing parametrization approaches attempting to account for unresolved orographic processes, such as turbulent form drag, low-level flow blocking or mountain waves, have been successful to some extent. They capture the basic impacts of the unresolved orography on atmospheric circulation in a qualitatively correct way and have led to significant progress in both numerical weather prediction and climate modelling. These approaches, however, have apparent limitations and inadequacies due to poor observational evidence, insufficient fundamental knowledge and an ambiguous separation between resolved and unresolved orographic scales and between different orographic processes. Numerical weather prediction and climate modelling has advanced to a stage where these inadequacies have become critical and hamper progress by limiting predictive skill on a wide range of spatial and temporal scales. More physically based approaches are needed to quantify the relative importance of apparently disparate orographic processes and to account for their combined effects in a rational and accurate way in numerical models. We argue that, thanks to recent advances, significant progress can be made by combining theoretical approaches with observations, inverse modelling techniques and high-resolution and idealized numerical simulations.
Similar content being viewed by others
Challenges in modelling orographic impacts on atmospheric circulation
Orography influences the atmospheric circulation through a wide range of processes and on a variety of spatial and temporal scales1,2 (Box 1, Fig. 1). Although orography can now be very accurately mapped using satellites at horizontal resolutions approaching tens of metres,3,4 the representation of its impacts on circulation in numerical weather prediction (NWP) and climate models remains notoriously difficult and several challenges must be overcome.
Unlike clouds or turbulence, which are completely unresolved even at global NWP resolutions of tens of km, the orographic spectrum is partially resolved by the model dynamics even at climate resolutions of hundreds of km. While certain orographic processes such as orographic gravity waves and low-level flow blocking become resolved at km-scale horizontal resolutions, turbulent form drag associated with small-scale hills remains unresolved even at O(~100 m) resolutions. This means that orography is within a ‘grey zone’ at resolutions currently used for global and even regional NWP and climate modelling.
Orographic effects on atmospheric circulation. a Island wake effects revealed by cloud-free regions in the lee of the Canary Islands, and von Karman vortices highlighted by the cloud spirals further downstream (Photo from the SeaWiFS Project, NASA/Goddard Space Flight Center, and ORBIMAGE, on 24 April 2000 used with permission from Visible Earth NASA); b Classical ‘v’ shape distinctive banded lee-wave pattern is visible in the clouds downstream of the Crozet Island over the southern Indian Ocean. The lifting and cooling of air on the crests of these waves lead to cloud formation, while sinking and heating leave the troughs cloud-free. (Photo from the Moderate Resolution Imaging Spectroradiometer (MODIS) on NASA’s Terra satellite on 9 April 2014 used with permission from Visible Earth NASA); c Downslope windstorms can lead to severe accelerations of the near-surface winds on the leeward side of the mountain, when the vertical propagation of waves is prevented by an elevated inversion-like region created by the breaking of large-amplitude waves close to the mountain top. Adapted from Whiteman.76 d Longitudinal variation of the disturbance of the geopotential height in the Charney–Eliassen model compared to the observed 500-hPa geopotential height perturbations at 45 N in January (top) and smoothed profile of topography at 45 N used in the Charney–Eliassen model (bottom). (Redrawn after Holton.77 with permission from Elsevier)
Parametrizations accounting for unresolved orographic processes, therefore, need to accurately capture the exchange between resolved and unresolved orographic drag as horizontal resolutions are varied from km to hundreds of km. Figure 2 illustrates that this exchange is not necessarily correctly captured in two very different models used for operational global weather forecasts.5,6 Particularly in the Northern Hemisphere mid-latitudes, the change in the parametrized orographic torque is larger than the change in the resolved orographic torque when the horizontal grid-spacing is refined from 150 to 16 km. As a result, the total orographic torque is not invariant with resolution, as would be expected based on angular momentum budget considerations (Box 2). This suggests that at climate model resolutions (~O(100 km)) the parametrized orographic torque is not representative of the mountain torque that is explicitly resolved at higher resolutions (~O(10 km)).
Difference in the resolved (green), parametrized (red) and total (resolved+parametrized, black) orographic torques between horizontal resolutions of 16 and 150 km. The torques are integrated over 10° latitude bands and averaged over a set of 24 h forecasts performed during December 2015 with models used for operational weather prediction at a the UK Met Office and b the European Centre for Medium-Range Weather Forecasts (ECMWF) b. The sign of the differences is such that the resolved westward torques between 30 and 60°N (which act as a drag on the westerly flow) are larger at 16 km compared to 150 km resolution, while the parametrized torques are smaller. The reduction in parametrized orographic torque greatly exceeds the increase in resolved orographic torque, leading to a smaller total orographic torque at higher resolution. The differences in the total (resolved+parametrized) orographic torques are, depending on latitude, between 20% and 40% of the total orographic torque in the UK Met Office model at 150 km resolution. See ref. 6 for further details of the methodology
The atmospheric momentum budget. Zonal averages (land points only) of a total parameterized surface stress, and contributions from b the turbulent friction and turbulent orographic form drag, and c low-level blocking and orographic gravity wave drag, from the results submitted by different groups to the Working Group for Numerical Experimentation of the World Meteorological Organization Drag project, for short range forecasts for January 2012
The formulations of orographic drag parameterizations also need to encompass processes acting across multiple scales and flow regimes (Box 1). By necessity, these parametrizations have so far mostly relied on simplified theoretical or empirical arguments targeted towards specific orographic processes in isolation. For gravity wave drag, the parametrizations are typically based on analytical solutions for simple flows over isolated mountains (dating back nearly 80 years7) using linear steady-state approximations to the equations of motion.8,9,10 For low-level flow blocking, they rely on simple empirical concepts for bluff-body dynamics.11 Numerical simulations12 and laboratory tank experiments13 of flow over idealized mountains have helped to refine these approaches, but evidence of how these concepts are applicable to more realistic and complex topography has only recently begun to emerge.14,15
It is also not clear how to properly account for the combined effects of the different orographic drag processes, which have thus far been dealt with in rather ad hoc ways. This is due both to missing fundamental knowledge of how these processes interact and the fact that orographic drag processes, and other drag processes, are not well constrained by observations. This leaves their representation in models, in terms of both magnitude and effects on circulation, exposed to compensating errors (Box 2).
Why does it matter?
Despite these challenges, existing orographic drag parametrizations capture the basic effects of unresolved orographic processes16,17,18 and have been instrumental in advancing weather forecasting and increasing the realism of the representation of the circulation in climate models over the past decades. The first orographic gravity wave drag parametrizations, introduced in operational NWP systems and climate models in the early 1980s,19,20 helped alleviate the excessively strong westerly flow in the upper troposphere, improved the representation of surface pressure in the northern hemisphere (NH) winter and reduced the stratospheric cold pole bias by >10 K. A parametrization for the low-level blocking of the flow due to unresolved mountains11 was also widely adopted and led to significant improvements in the predictive skill of medium-range weather forecasts. For example, in the Canadian global NWP system it led to a far bigger improvement in skill during the NH winter than any other individual change made in the past 15 years.21 Accounting for the turbulent orographic form drag from small-scale (<5 km horizontal) hills17,22 also greatly contributed to increases in predictive skill of weather forecasts. Figure 4 illustrates that the predictive skill of 10-day forecasts dramatically decreases by the equivalent of 1 day during winter in the NH if this parametrization is removed from a global NWP system. This is equivalent to the weather forecast skill gained over the past decade through continuous improvements to the global NWP systems.23
Almost 1 day of skill is lost when the turbulent orographic form drag parametrization17 is switched off in global 10-day weather forecasts performed with the Integrated Forecasting System of the European Centre for Medium-Range Weather Forecasts: in the control experiment (black), forecasts 7 days ahead have an accuracy of 80% in terms of anomaly correlation of the geopotential height at 500 hPa, while in the experiment where the form drag scheme was switched off (red) this level of accuracy is lost after 6 days. In other words, in the new experiment the degree of accuracy of the forecasts only matches the degree of accuracy of numerical weather prediction systems of 10 years ago.23 The simulations have been performed at a horizontal resolution of 32 km, for the period December–February 2016–2017
Given this circulation sensitivity to parametrized orographic drag, uncertainties in its representation (Fig. 3) were unsurprisingly found to impact the skill of weather forecasts on daily to seasonal timescales.24 Since the parameterized orographic drag contributes substantially to the momentum budget within climate models,25 its representation and uncertainties related to it have also been found to be important for climate model fidelity26,27 and for regional aspects of climate change.25,28
The circulation sensitivity to parametrized orographic drag and the large uncertainty related to these processes highlighted in the past few years motivates the need to make advances in their representation in Earth system models. Reducing these uncertainties would allow a leap forward in predictive skill across the entire range of temporal and spatial scales. While some aspects of orographic drag parametrizations may become obsolete with resolution upgrades in NWP in the next few decades, most aspects will remain relevant for the foreseeable future. For example, form drag and flow separation across small hills only become resolved at O(100 m) and will hence still need to be parametrized in models used for predictions from hours to decades. Low-level flow blocking or gravity wave effects become resolved at km-scale, but restrictions on resolution in ensemble forecast systems and climate projections will mean that these effects will need to be parametrized in models used for these applications for many years to come.
What is needed to make progress?
We argue that, thanks to recent advances in numerical models, computing techniques, observational analysis and retrieval and fluid dynamics theory, there is now scope to significantly improve our understanding of orographic drag processes and their representation in models by pursuing the three avenues detailed below.
Observational constraints and inverse modelling
It is currently impossible to directly observe the three-dimensional distribution of momentum flux induced by orographic features at global scale or even over extended mountain ranges. However, recent developments open exciting opportunities for constraining at least one of the orographic processes: mountain waves. Recent field campaigns, such as the DEEPWAVE29 field experiment in New Zealand, provide in situ aircraft measurements of wave properties (including momentum fluxes). Satellite observations offer a wealth of information for constraining the representation of gravity waves,30 and significant recent advances in methods of deriving gravity wave characteristics (wavelength, propagation, amplitude) from such observations31,32 offer new possibilities for using this information to evaluate the representation of orographic gravity waves in models. Although difficulties still exist in comparing these observations with models, progress has also been made in diagnostic techniques allowing such comparisons.33,34 Space-borne or ground-based lidar observations are also increasingly being used to explore gravity wave characteristics and their representation in models.35,36
Using analyses or reanalyses (our best guess of the atmospheric state) for examining systematic short-range forecast errors has proven fruitful for attributing errors due to orographic drag,15,37,38,39 since the errors remain fixed over the orography itself at short lead times. While these techniques have been and are routinely utilized to evaluate NWP models, there is also value in applying them towards understanding model errors in lower-resolution climate models40 and such studies could be done more routinely.
The development of sophisticated mathematical and statistical techniques in the past years, especially in the context of data assimilation and ensemble forecasting, also offers new ways of constraining uncertain parameters within, and errors associated with, orographic drag parametrizations. For example, inverse modelling techniques employing data assimilation,41,42 perturbed parameter ensembles43 and statistical emulators,44,45 can be used to recover information on uncertain model parameters by fitting the model forecast to observed data, such as winds, temperature or pressure. Some of these techniques have been applied to orographic drag processes in simplified models.42 Applying them to NWP and climate models seems very promising. To optimize a parametrized process through data assimilation, for example, it is necessary to have one or more parameters that are not well constrained. At the same time, it is also necessary to have an observation that is informative about that process or parameter. Surface stress is a good candidate because surface pressure responds to surface stress,20 and surface pressure is a well-observed quantity over land. The match of surface pressure to observations could be optimized by adjusting surface stress at each model grid point. This can be achieved, for example, through an ‘augmented control variable’ approach, which is now available in complex global data assimilation systems.46
High-resolution simulations
With increasing computational power and improvements in numerical methods, comprehensive high-resolution simulations with spatial resolutions that can realistically47 capture the fluid dynamics over complex mountain terrain at scales relevant for improving orographic drag parametrizations are becoming increasingly available. Such simulations can be considered as high-resolution virtual laboratories for exploring orographic drag processes. The added benefit of using such simulations over realistic complex topography initialised from our best guess of the observed atmospheric state, as opposed to idealised ones, is that they allow us to quantify (in real terms) the contribution of the parametrized orography to the model error.15
Studies with comprehensive high-resolution models have already been successfully used to demonstrate the improved representation of flow around orography at increased resolutions on mesoscales.48 Km-scale simulations at which low-level blocking and orographic gravity waves become resolved have also been used to demonstrate the potential of existing parametrizations to capture the time mean and the variability of the resolved orographic drag and to explore their limitations for small islands with real terrain.14,18 We are now entering an era where such simulations become feasible over extensive and complex mountain ranges such as the Himalayas,15 the Rockies and even globally.49
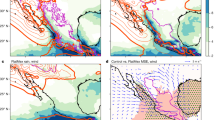
As an example, Fig. 5 compares the monthly averaged zonal momentum flux by resolved gravity waves in a high-resolution (2 km) regional simulation over the Rockies with the parametrized momentum flux in an equivalent low-resolution (32 km) simulation. The resolved momentum flux has been derived from the 2-km model-simulated velocity fields, which explicitly resolve the orographic gravity waves. In this case, it appears that the parametrized momentum flux in the low-resolution model provides a reasonable representation of the well-resolved ‘truth’.
The mean zonal component of gravity wave momentum flux (N m−2) at 7 km above sea level as predicted by 1-month-long simulations (December 2015) of flow across the Rockies with the Met Office Unified Model. The right-hand panel shows the parametrized flux produced by a simulation with a coarse (32 km) grid. The left-hand panel shows the simulated flux resolved on a much finer (2 km) grid, after it has been coarse-grained onto the 32 km grid. Comparison of the two momentum flux fields allows one to determine the realism of the parametrization scheme
Spectral filtering methods50 used to isolate the gravity wave velocity perturbations in order to compute the momentum fluxes, as are employed in Fig. 5, can be used to determine the spectral contributions to momentum fluxes in high-resolution simulations. Since much of the gravity wave parametrization theory is based on linear wave solutions, this allows for a direct comparison of the scale dependence of the orographic drag deduced from the models with the analytical one, as had been done previously with observed momentum fluxes.51 Pursuing such an approach in the future is highly relevant to the parametrization problem, since it allows both to determine the dominant scales contributing towards the resolved momentum fluxes (and therefore, which scales the parametrizations need to account for) and to evaluate the validity of the theory.
Future analysis of km-scale experiments should be targeted towards understanding: how orographic drag is distributed in the horizontal and vertical domain; how this distribution depends on the flow characteristics, namely the thermal stratification, the wind speed and wind direction over mountain ranges of different sizes (e.g. Pyrenees, Alps, Himalayas, Rockies, etc.) as well as isolated mountains (e.g. Kilimanjaro, Fuji); and which processes contribute to the total orographic drag. Particular emphasis should be given to processes that are currently not accounted for in parametrizations, such as lee-wave drag and transient wave–mean flow interaction, so that the consequences of their omission may be evaluated.
Simulations at even higher resolution (O(100 m)), which can start to resolve turbulent form drag associated with orographic features with scales <5 km, are also becoming available at continental scale.52 These could be used in the future to help constrain the partitioning between form drag and the other orographic drag processes.
Better theoretical understanding
The focus on orographic drag processes in recent years has highlighted the gaps in our theoretical understanding of these processes. One of the key gaps lies in the partitioning between different drag processes, illustrated by the inter-model spread in surface stress shown in Fig. 3. This discrepancy may be due to missing processes not accounted for and/or simplifications made in the parametrizations. Theories for more complex parametrizations, for example, accounting for drag effects due to vertical windshear,53 downslope windstorms54 and transient gravity wave–mean flow interaction55 do exist. However, simple approximations are maintained in global models due to the considerable leap that needs to be made from idealized theory to practical implementation of a parameterization scheme suitable for weather and climate models. There are also several processes that are not well understood theoretically and are not incorporated into existing parametrizations, such as mean flow time dependence56 and the interactions of multiple scales of topography in a stratified flow.57
A better theoretical understanding of the large-scale circulation response to different forms of orographic drag, such as the non-local response to a torque,58,59 is also required. If these responses would be understood, one could use the indirect or far-field response to a certain process to obtain a ‘fingerprint’ of that process and to evaluate its accuracy. An example is the way in which the amplitude and period of the Quasi-Biennial Oscillation is used as a constraint on the non-orographic gravity wave drag.60
Progress at both the process level and in terms of circulation impacts can be achieved by combining a hierarchical modelling approach with our existing theoretical knowledge. In addition to the high-resolution simulations with realistic terrain, simulations that start from well-known idealized mountain shapes in idealized flow, for which we have analytical solutions, and gradually increase in complexity towards real-world mountain ranges in real flow can showcase the limitations of established concepts and provide a quantitative basis for new understanding. Idealized general circulation experiments, in which drag is prescribed with different geographical or vertical distributions, could also be used to develop observable large-scale fingerprints of different processes contributing to drag as a means of constraining the partitioning of drag. These will help to bridge the gap between the simplifications made in current parametrizations, the available theory and more advanced parametrizations.
A promising future for orographic drag
Key challenges in representing orographic drag processes include the ‘grey-zone’ problem, which encompasses the unclear separation between resolved and unresolved orographic scales, the overlap between different processes and the difficulties in directly observing orographic drag. Overcoming these issues will be instrumental in the development of a future generation of increasingly accurate weather and climate models. Rapid progress is within reach by making combined use of theoretical approaches, emerging observational constraints and inverse modelling and high-resolution simulations along the avenues exposed within this perspective.
References
Smith, R. B. The influence of mountains on the atmosphere. Adv. Geophys. 21, 87–230 (1979).
Held, I. M., Ting, M. & Wang, H. Northern winter stationary waves: theory and modeling. J. Clim. 15, 2125–2144 (2002).
Rizzoli, P. et al. Generation and performance assessment of the global TanDEM-X digital elevation model. ISPRS J. Photogramm. Remote Sens. 132, 119–139 (2017). ISSN 0924-2716.
ASTER GDEM Validation Team. ASTER Global Digital Elevation Model Version 2. http://www.jspacesystems.or.jp/ersdac/GDEM/ver2Validation/Summary_GDEM2_validation_report_final.pdf (2011).
Brown, A. R. Resolution dependence of orographic torques. Q. J. R. Meteorol. Soc. 130, 3029–3046 (2004).
van Niekerk, A., Shepherd, T. G., Vosper, S. B. & Webster, S. Sensitivity of resolved and parametrized surface drag to changes in resolution and parametrization. Q. J. R. Meteorol. Soc. 142, 2300–2313 (2016).
Queney, P. The problem of air flow over mountains: a summary of theoretical studies. Bull. Am. Meteor. Soc. 29, 16–26 (1948).
Phillips, D. S. Analytical surface pressure and drag for linear hydrostatic flow over three-dimensional elliptical mountains. J. Atmos. Sci. 41, 1073–1084 (1984).
Smith, R. B. Linear theory of stratified hydrostatic flow past an isolated mountain. Tellus 32, 348–364 (1980).
Lindzen, R. S. Turbulence and stress owing to gravity wave and tidal breakdown. J. Geophys. Res. 86(C10), 9707–9714 (1981).
Lott, F. & Miller, M. J. A new subgrid‐scale orographic drag parametrization: Its formulation and testing. Q. J. R. Meteorol. Soc. 123, 101–127 (1997).
Kim, Y. & Arakawa, A. Improvement of orographic gravity wave parameterization using a mesoscale gravity wave model. J. Atmos. Sci. 52, 1875–1902 (1995).
Boyer, D. L. & Davies, P. A. Laboratory studies of orographic effects in rotating and stratified flows. Annu. Rev. Fluid. Mech. 32, 165–202 (2005).
Vosper, S. B., Brown, A. R. & Webster, S. Orographic drag on islands in the NWP mountain grey zone. Q. J. R. Meteorol. Soc. 142, 3128–3137 (2016).
van Niekerk, A., Sandu, I., & Vosper, S., The circulation response to resolved versus parametrized orographic drag over complex mountain terrains J. Adv. Model. Earth Syst. 10. https://doi.org/10.1029/2018MS001417 (2018).
Zadra, A., Roch, M., Laroche, S. & Charron, M. The subgrid‐scale orographic blocking parametrization of the gem model. Atmos. Ocean 41, 155–170 (2003).
Beljaars, A. C., Brown, A. R. & Wood, N. A new parametrization of turbulent orographic form drag. Q. J. R. Meteorol. Soc. 130, 1327–1347 (2004).
Vosper, S. B. Mountain waves and wakes generated by South Georgia: implications for drag parametrization. Q. J. R. Meteorol. Soc. 141, 2813–2827 (2015).
Palmer, T. N., Shutts, G. J. & Swinbank, R. Alleviation of a systematic westerly bias in general circulation and numerical weather prediction models through an orographic gravity wave drag parametrization. Q. J. R. Meteorol. Soc. 112, 1001–1039 (1986).
McFarlane, N. A. The effect of orographically excited gravity wave drag on the general circulation of the lower stratosphere and troposphere. J. Atmos. Sci. 44, 1775–1800 (1987).
Charron, M. et al. The stratospheric extension of the canadian global deterministic medium-range weather forecasting system and its impact on tropospheric forecasts. Mon. Weather Rev. 140, 1924–1944 (2012).
Wood, N. & Mason, P. The pressure force induced by neutral, turbulent flow over hills. Q. J. R. Meteorol. Soc. 119, 1233–1267 (1993).
Bauer, P., Thorpe, A. & Brunet, G. The quiet revolution of numerical weather prediction. Nature 525, 47–55 (2015).
Sandu, I. et al. Impacts of parameterized orographic drag on the Northern Hemisphere winter circulation. J. Adv. Model. Earth Syst. 8, 196–211 (2016).
van Niekerk, A., Scinocca, J. F. & Shepherd, T. G. The modulation of stationary waves, and their response to climate change, by parameterized orographic drag. J. Atmos. Sci. 74, 2557–2574 (2017).
Lindvall, J., Svensson, G. & Caballero, R. The impact of changes in parameterizations of surface drag and vertical diffusion on the large-scale circulation in the Community Atmosphere Model (CAM5). Clim. Dyn. 48, 3741–3758 (2017).
Pithan, F., Shepherd, T. G., Zappa, G. & Sandu, I. Climate model biases in jet streams, blocking and storm tracks resulting from missing orographic drag. Geophys. Res. Lett. 43, 7231–7240 (2016).
Sigmond, M. & Scinocca, J. F. The influence of the basic state on the Northern Hemisphere circulation response to climate change. J. Clim. 23, 1434–1446 (2010).
Fritts, D. C. et al. The deep propagating gravity wave experiment an airborne and ground-based exploration of gravity wave propagation and effects from their sources throughout the lower and middle atmosphere. Bull. Am. Meteor. Soc. 97, 425–453 (2016).
Alexander et al. Recent developments in gravity‐wave effects in climate models and the global distribution of gravity‐wave momentum flux from observations and models. Q. J. R. Meteorol. Soc. 136, 1103–1124 (2010).
Wright, C. J., Hindley, N. P., Hoffmann, L., Alexander, M. J. & Mitchell, N. J. Exploring gravity wave characteristics in 3-D using a novel S-transform technique: AIRS/Aqua measurements over the Southern Andes and Drake Passage. Atmos. Chem. Phys. 17, 8553–8575 (2017).
Krisch, I. et al. First tomographic observations of gravity waves by the infrared limb imager GLORIA. Atmos. Chem. Phys. 17, 14937–14953 (2017).
Wells, H., Vosper, S. B. & Yan, X. An assessment of a mountain‐wave parametrization scheme using satellite observations of stratospheric gravity waves. Q. J. R. Meteorol. Soc. 137, 819–828 (2011).
Rapp, M., Dörnbrack, A. & Preusse, P. Large midlatitude stratospheric temperature variability caused by inertial instability: a potential source of bias for gravity wave climatologies. Geophys. Res. Lett. 45, 682–10,690 (2018).
Ehard, B. et al. Comparing ECMWF high‐resolution analyses with lidar temperaturemeasurements in the middle atmosphere. Q J. R. Meteorol. Soc. 144, 633–640 (2018).
Le Pichon, R. S. et al. Comparison of co-located independent ground-based middle atmospheric wind and temperature measurements with numerical weather prediction models. J. Geophys. Res. Atmos. 120, 8318–8331 (2015).
Tibaldi, S. Envelope orography and maintenance of the quasi-stationary circulation in the ECMWF global models. Adv. Geophys. l29, 339–374 (1986).
Klinker, E. & Sardeshmukh, P. D. The diagnosis of mechanical dissipation in the atmosphere from large-scale balance requirements. J. Atmos. Sci. 49, 608–627 (1992).
Rontu, L. Vorticity budget over mountains, estimated from HIRLAM analyses and forecasts. Met. Z. 15, 199–206 (2006).
Ma, H. et al. On the correspondence between mean forecast errors and climate errors in CMIP5 models. J. Clim. 27, 1781–1798 (2014).
Pulido, M. A simple technique to infer the missing gravity wave drag in the middle atmosphere using a general circulation model: potential vorticity budget. J. Atmos. Sci. 71, 683–696 (2014).
Tandeo, P., Pulido, M. & Lott, F. Offline parameter estimation using EnKF and maximum likelihood error covariance estimates: application to a subgrid‐scale orography parametrization. Q. J. R. Meteorol. Soc. 141, 383–395 (2015).
Ollinaho, P., Laine, M., Solonen, A., Haario, H. & Järvinen, H. NWP model forecast skill optimization via closure parameter variations. Q. J. R. Meteorol. Soc. 139, 1520–1532 (2013).
Murphy, J. M. et al. Quantification of modelling uncertainties in a large ensemble of climate change simulations. Nature 430, 768–772 (2004).
McNeall, D. et al. The impact of structural error on parameter constraint in a climate model. Earth Syst. Dynam 7, 917–935 (2016).
Hamill, T. M. & Snyder, C. A hybrid ensemble Kalman filter–3D variational analysis scheme. Mon. Weather Rev. 128, 2905–2919 (2000).
Shutts, G. J. & Vosper, S. B. Stratospheric gravity waves revealed in NWP model forecasts. Q. J. R. Meteorol. Soc. 137, 303–317 (2011).
Chan, P. W. & Hon, K. K. Performance of super high resolution numerical weather prediction model in forecasting terrain‐disrupted airflow at the Hong Kong International Airport: case studies. Met. Appl. 23, 101–114 (2016).
Holt, L. A. et al. An evaluation of gravity waves and gravity wave sources in the Southern Hemisphere in a 7 km global climate simulation. Q. J. R. Meteorol. Soc. 143, 2481–2495 (2017).
Kruse, C. G. & Smith, R. B. Gravity wave diagnostics and characteristics in mesoscale fields. J. Atmos. Sci. 72, 4372–4392 (2015).
Smith, R. B. et al. Stratospheric gravity wave fluxes and scales during DEEPWAVE. J. Atmos. Sci. 73, 2851–2869 (2016).
Heinze, R. et al. Large-eddy simulations over Germany using ICON: a comprehensive evaluation. Q. J. R. Meteorol. Soc. https://doi.org/10.1002/qj.2947 (2016).
Teixeira, M. A. & Miranda, P. M. A linear model of gravity wave drag for hydrostatic sheared flow over elliptical mountains. Q. J. R. Meteorol. Soc. 132, 2439–2458 (2006).
Scinocca, J. F. & McFarlane, N. A. The parametrization of drag induced by stratified flow over anisotropic orography. Q. J. R. Meteorol. Soc. 126, 2353–2393 (2000).
Bölöni, G. et al. The interaction between atmospheric gravity waves and large-scale flows: an efficient description beyond the nonacceleration paradigm. J. Atmos. Sci. 73, 4833–4852 (2016).
Chen, C.‐C., Hakim, G. J. & Durran, D. R. Transient mountain waves and their interaction with large scales. J. Atmos. Sci. 64, 2378–2400 (2007).
Kruse, C. G. & Smith, R. B. Non-dissipative and dissipative momentum deposition by mountain wave events in sheared environments. J. Atmos. Sci. 75, 2721–2740 (2018).
Simpson, I. R. & Polvani, L. M. Revisiting the relationship between jet position, forced response, and annular mode variability in the southern midlatitudes. Geophys. Res. Lett. 43, 2896–2903 (2016).
Chen, G. & Zurita-Gotor, P. The tropospheric jet response to prescribed zonal forcing in an idealized atmospheric model. J. Atmos. Sci. 65, 2254–2271 (2008).
Scaife, A. A., Butchart, N., Warner, C. D. & Swinbank, R. Impact of a spectral gravity wave parameterization on the stratosphere in the Met Office Unified Model. J. Atmos. Sci. 59, 1473–1489 (2002).
Baines, P. G. Topographic Effects in Stratified Flows (Cambridge University Press, Cambridge, 1998).
Teixeira, M. A. C. The physics of orographic gravity wave drag. Front. Phys. 2, 43 (2014).
Ralph, F. M., Neiman, P. J. & Levinson, D. Lidar observations of a breaking mountain wave associated with extreme turbulence. Geophys. Res. Lett. 24, 663–666 (1997).
Peltier, W. R. & Clark, T. L. The evolution and stability of finite-amplitude mountain waves. Part II: Surface wave drag and severe downslope windstorms. J. Atmos. Sci. 36, 1498–1529 (1979).
McLandress, C., Shepherd, T. G., Polavarapu, S. & Beagley, S. R. Is missing orographic gravity wave drag near 60°S the cause of the stratospheric zonal wind biases in chemistry–climate models? J. Atmos. Sci. 69, 802–818 (2012).
Charney, J. G. & Eliassen, A. A numerical method for predicting the perturbations of the middle latitude Westerlies. Tellus 1, 38–54 (1949).
Holton, J. R. The role of gravity wave induced drag and diffusion in the momentum budget of the mesosphere. J. Atmos. Sci. 39, 791–799 (1982).
Simpson, I. R., Bacmeister, J. T., Sandu, I. & Rodwell, M. J. Why do modeled and observed surface wind stress climatologies differ in the trade wind regions? J. Clim. 31, 491–513 (2018).
Bougeault, P. et al. PYREX: a summary of findings. Bull. Am. Meteor. Soc. 78, 637–650 (1997).
Rosen, R. D. & Salstein, D. A. Variations in atmospheric angular momentum on global and regional scales and the length of day. J. Geophys. Res. 88, 5451–5470 (1983).
Boer, G. J. Earth‐atmosphere exchange of angular momentum simulated in a general circulation model and implications for the length of day. J. Geophys. Res. 95, 5511–5531 (1990).
Sandu, I., Beljaars, A., Bechtold, P., Mauritsen, T. & Balsamo, G. Why is it so difficult to represent stably stratified conditions in numerical weather prediction (NWP) models?. J. Adv. Model. Earth Syst. 5, 117–133 (2013).
Hourdin, F. et al. The art and science of climate model tuning. Bull. Am. Meteor. Soc. 98, 589–602 (2017).
Sandu, I., Zadra, A. & Wedi, N. On the impact of orographic drag on forecast skill, ECMWF Newsletter, Winter 2016/2017.
Zadra, A. WGNE Drag Project: An Inter-model Comparison of Surface Stresses. Technical Report [http://collaboration.cmc.ec.gc.ca/science/rpn/drag_project/documents/wgne_drag_project_report01.pdf] (2013).
Whiteman, D. C. Mountain Meteorology: Fundamentals and Applications. (Oxford University Press, 2000).
Holton, J. & Hakim, G. J. An Introduction to Dynamic Meteorology, Vol. 88, 5th ed., (Imprint: Academic Press, Elsevier, 2012).
Acknowledgements
The authors would like to acknowledge Nils Wedi, Piotr Smolarkiewicz, François Lott and Steve Derbyshire for useful discussions about the ways forward towards improving the representation of orographic effects in numerical models and the two anonymous reviewers for their constructive comments and suggestions.
Author information
Authors and Affiliations
Contributions
I.S., A.v.N., T.G.S. and S.V. conceived and wrote a first draft of the manuscript, based on discussions at the ECMWF drag workshop in September 2016 that was attended by all authors. A.v.N. provided Fig. 2, A.Z. provided Fig. 3, I.S. provided Fig. 4, S.V. provided Fig. 5. N.M. wrote the abstract. All other authors provided comments, suggested edits and contributed additional expertise in proposing the three avenues for making progress. All authors provided comments and suggested edits for the initially submitted draft and the changes made during the review process and approved the final draft.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sandu, I., van Niekerk, A., Shepherd, T.G. et al. Impacts of orography on large-scale atmospheric circulation. npj Clim Atmos Sci 2, 10 (2019). https://doi.org/10.1038/s41612-019-0065-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-019-0065-9
This article is cited by
-
Evolving winter atmospheric teleconnection patterns and their potential triggers across western North America
npj Climate and Atmospheric Science (2024)
-
Investigating monthly geopotential height changes and mid-latitude Northern Hemisphere westerlies
Theoretical and Applied Climatology (2024)
-
Climate change information over Fenno-Scandinavia produced with a convection-permitting climate model
Climate Dynamics (2023)
-
Characteristics for the sources and sinks of gravity waves in an orographic heavy snowfall event
Frontiers of Earth Science (2023)
-
Importance of orographic gravity waves over the Tibetan Plateau on the spring rainfall in East Asia
Science China Earth Sciences (2023)