Abstract
We review the growing evidence for a widespread inconsistency between the low strength of predictable signals in climate models and the relatively high level of agreement they exhibit with observed variability of the atmospheric circulation. This discrepancy is particularly evident in the climate variability of the Atlantic sector, where ensemble predictions using climate models generally show higher correlation with observed variability than with their own simulations, and higher correlations with observations than would be expected from their small signal-to-noise ratios, hence a ‘signal-to-noise paradox’. This unusual behaviour has been documented in multiple climate prediction systems and in the response to a number of different sources of climate variability. However, we also note that the total variance in the models is often close in magnitude to the observed variance, and so it is not a simple matter of models containing too much variability. Instead, the proportion of Atlantic climate variance that is predictable in climate models appears to be too weak in amplitude by a factor of two, or perhaps more. In this review, we provide a range of examples from existing studies to build the case for a problem that is common across different climate models, common to several different sources of climate variability and common across a range of timescales. We also discuss the wider implications of this intriguing paradox.
Similar content being viewed by others
Introduction
The idea that there is unpredictable variability in the weather and climate has been demonstrated in the seminal papers by Ed Lorenz1,2 and is popularised as ‘chaos’ and the ‘butterfly effect’: whereby a tiny disturbance such as the flap of a butterfly’s wings can grow into large-scale differences in future weather patterns. This leads to inherent uncertainty in any practical meteorological forecast and suggests fundamental limits on the predictability of the climate system. This sensitivity to initial conditions led to the ideas behind the development of ensemble weather prediction involving multiple numerical realisations;3 an approach that was subsequently extended to longer range forecasts4 and is now routinely used in seasonal predictions5 and longer climate projections.6 In these ensemble prediction systems, individual member simulations differ by small perturbations, which grow with time due to unpredictable variability7 or ‘chaos’, limiting predictability but also allowing the ensemble to capture the uncertainty in the future state of the system that arises due to uncertainty in initial conditions and/or model formulation. Although the underlying equations in climate and weather prediction models are fundamentally deterministic, and are therefore not random, the range of outputs from ensemble predictions is often treated probabilistically when either measuring the skill of retrospective predictions8,9 or expressing the outcome of a particular forecast.10
Estimates of the time horizon for predictability of individual weather events is typically 2 weeks for the mid-latitude atmosphere.11,12 However, some components of the climate system are predictable well beyond these timescales. For example, the Madden Julian Oscillation,13 El Niño-Southern Oscillation,14 Atlantic Multidecadal Variability15,16 and the Quasi-Biennial Oscillation17 are all predictable at monthly, seasonal or even longer timescales. Importantly, these sources of predictable variability also have remote teleconnections,18,19 leading to predictability in mid-latitude surface climate (i.e., average weather conditions) at seasonal and decadal lead times.
Given this, in the following section we assess the predictability for both observed (O) and model ensemble member (M) regional climate by dividing the temporal variability into predictable (signal, S) and unpredictable (noise, N) components:20,21
A signal-to-noise paradox in climate predictions
In order to demonstrate the existence of a signal-to-noise paradox we now compare the signal and noise components of observations and models. Climate model predictions, initialised with observational analyses and using fully coupled ocean–atmosphere models, now show potentially useful levels of prediction skill for year to year variations in the winter North Atlantic Oscillation (NAO). This implies predictability of European and North American winter climate out to a season or even longer ahead.20,22,23,24,25,26,27,28,29
All of these studies use ensembles and create an ensemble mean model prediction M to reduce the level of unpredictable noise:
where n is the number of ensemble members.
If the ensembles are run for a number of historical cases, for example, a series of past winters, then the squared correlation rmo,2 between the year to year variability in the model ensemble mean M(t) (where time t denotes a particular year) and the observed variability O(t) provides an estimate of the predictable fraction of the observed variance30:
where σSo2 and σNo2 are the variances of the signal and noise components of the observations, respectively.
In the limit of a large ensemble (n → ∞), Eq. (2) implies that the model noise vanishes and the ensemble mean consists of only the modelled predictable signal Sm. The proportion of modelled variance that is predictable may therefore be obtained as the variance of Sm divided by the total variance of individual model members. Eade et al.20 used these definitions of observed and modelled predictability to define the ratio of predictable components (RPC) between observations and model:
In principle, the RPC should be 1, as the observations and model should contain the same proportion of predictable variance and the squared correlation should match the predictable proportion of variance in the model.
If the RPC is less than one, then the correlation of the model ensemble mean with observations (rmo) is smaller than would be expected from the predictable fraction of variance in the model. RPC values below 1 are commonly found in climate predictions, especially in tropical seasonal predictions.20,31 This can be caused by several factors, including too few ensemble members to eliminate unpredictable noise, a lack of spread in the forecast ensemble, systematic errors in predicted signals such as poorly structured teleconnections or imperfect initialisation leading to ‘shocks’ in the forecasts.
If on the other hand, RPC is greater than one, then the correlation is higher than would be expected from the proportion of signal in the ensemble variance. RPC values above 1 were not generally expected, but this second possibility has been considered32 and examples have now been found in a number of different ensemble seasonal predictions, particularly in winter predictions of the NAO and Arctic Oscillation.21,23,25,28,29 For example, in the seasonal forecasts of the NAO reported by Scaife et al.,23 the predictable ensemble mean signal was around 2 hPa, the total ensemble variability was around 8 hPa and the correlation was around 0.6 so the RPC = 0.6/(2./8.) > 2. The high correlation score is therefore inconsistent with the small predictable signal in the model and it has been shown that the discrepancy is highly statistically significant21, hence a ‘signal-to-noise paradox’.26
An interesting consequence of the signal-to-noise paradox comes from the alternate form of Eq. (4) based on correlations alone:
If RPC > 1, then Eq. (5) implies that the correlation between the model ensemble mean and the observations (rmo) exceeds the average correlation between the model ensemble mean and a single ensemble member (rmm). In this case we arrive at the counterintuitive result that the model is better at predicting the real world than it is at predicting itself.20 Figure 1 illustrates this explicitly for a set of seasonal predictions of the NAO. The correlation of the modelled NAO (black line) climbs with ensemble size due to the suppression of unpredictable noise (Eq. (2)), asymptoting at the predictable limit where a very large ensemble has suppressed all noise. If we replace the observations with a single ensemble member (without replacement in the ensemble mean so as to avoid artificially high correlations between members with the same realisation of noise), then the resulting correlation should ideally be the same, as each ensemble forecast member is meant to represent an alternate, but perfectly viable version of the observed evolution.
Predictability of the North Atlantic Oscillation in the real world (black) is higher than the predictability in the model (blue). The effects of ensemble size on seasonal hindcasts of the winter North Atlantic Oscillation are plotted. The black line shows the average correlation score when different size ensemble averages are correlated with the observed NAO (rmo). The blue line shows the same quantity when ensemble means are correlated with a single forecast member (rmm). The black dotted line is a theoretical fit to the solid black line.23 The skill grows with ensemble size due to the suppression of unpredictable noise, but in principle the curves should be the same. In practice the model is better able to predict the real world than itself. Data are from the GloSea5 forecast system23
However, as shown in Fig. 1, in practise the correlation between the ensemble mean and observations (rmo) is higher than the correlation between the ensemble mean and individual ensemble members (rmm), yielding an RPC value in excess of 2 as explained above, and suggesting that the model is better able to predict the real world than it is able to predict itself. Now as the total ensemble standard deviation (σSm2 + σNm2) is close to the observed variability of 8 hPa, the only remaining term in Eq. (4) is the signal standard deviation (σSm) which must therefore be at least two times too small. Note that independent sets of ensemble predictions give a similar result26 and other climate models show similar effects in their predictions of the NAO and AO.22,25,28,29
Note also that practical calculations of the RPC are expected to be underestimates of the true value.20 This is because any practical ensemble is finite in size and so the correlation with observations (rmo) will likely be lower than that of an infinite ensemble. Furthermore, the ensemble mean variance (σSm2) will likely be higher than that of an infinite ensemble due to incomplete suppression of noise. According to Eq. (4), the RPC from any practical ensemble is therefore also likely to be an underestimate. We deduce that ensemble mean signals are likely more than two times too small for the NAO and recommend use of Eq. (5) to calculate the RPC as it is an unbiased estimate.
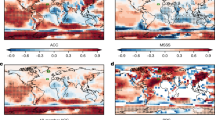
Finally, as noted above, the signal-to-noise paradox is not only limited to the NAO. Although it is clearest in and around the Atlantic basin, it also occurs in parts of the Pacific and the southern hemisphere (Fig. 2) where it occurs in predictions of the Southern Annular Mode.33 Similar situations have been found on longer timescales in both interannual and decadal predictions20,26,34,35 and in other predicted variables such as surface temperature,20 wind,28 and rainfall.20,36
The signal-to-noise paradox is mainly in the North Atlantic but also exists elsewhere. Ratio of predictable components (RPC) for seasonal predictions of winter sea level pressure. Orange and red values indicate RPC > 1 whereas blue and green values indicate RPC < 1. Hatched areas are statistically significantly different from 1 at the 90% confidence level. Data are from the GloSea5 forecast system, Figure courtesy of Eade et al.20
A signal-to-noise paradox in atmosphere-only models
So far we have seen that initialised climate predictions of the atmospheric circulation in the Atlantic sector exhibit a signal-to-noise paradox, where they are better at predicting the real world than they are at predicting themselves. In this section we show that this idea could potentially explain a number of earlier results from atmosphere-only climate models forced by specified ocean conditions, and that the signal-to-noise paradox appears to have been present in generations of previous climate models.
Early studies of NAO variability and its potential predictability, given specified ocean surface conditions, gave moderate, but highly significant correlations with observations if enough ensemble members were used to eliminate unpredictable variability in the model.37,38,39 This important result suggested that their might be significant long-range predictability of the winter NAO (as has since been demonstrated), but it was inconclusive at the time because these were not actual forecasts. The specified ocean conditions in these experiments contained information from the future and in particular, this contained information about the subsequent behaviour of the NAO, as the NAO leaves a tripolar imprint in ocean temperatures40 which could feedback to the atmosphere. Careful arguments were put forward to suggest that reproducibility of the observed NAO variability in atmosphere-only model experiments might therefore be due to the limitations of the experiment in specifying the future ocean conditions, and that this could give a misleading overestimate of actual predictability.41 Despite this limitation, ensembles of these atmospheric simulations appear to have contained the same paradoxical result found in long-range forecasts and discussed in the previous section. Figure 3 shows the skill of reproducing NAO variability in one such ensemble of atmospheric model simulations. The same slow climb of correlation skill with ensemble size occurred (blue curve), and the correlation between the ensemble mean and the observed NAO, although modest, ultimately rose to a level exceeding the typical correlation with single ensemble members (black dots). Given the striking similarity between these results and results from the coupled model predictions in Fig. 1, it appears that that these early simulations were subject to the same signal-to-noise paradox.
Reproducibility of observed NAO variability in an atmospheric climate model with prescribed observed SST variations. The blue curve is for the model ensemble mean correlated with the observed NAO. Note how it almost always shows higher correlations than when the model ensemble mean is compared with one of its own members (black dots). Although unimportant for this review, the red curve shows correlation of low-frequency NAO variability with observations. Dots show individual random subsamples with the same ensemble size. From Mehta et al.38
Other atmosphere model experiments suggest that the signal-to-noise paradox might also be present on multidecadal timescales. Although it has since declined,42 the large multidecadal increase of the NAO from its low values in the 1960s to its very high values in the early 1990s has been the subject of many studies. The mechanisms behind this shift are still only partly understood and studies have linked it to changes in the Indian ocean basin,43 changes in the stratosphere,44 changes in the tropics,45,46 simple internal variability,47 coupled ocean–atmosphere cycles,48 or even climate change.49,50 However, there is a common thread to many of these studies, in that (apart from very rare exceptions) these experiments consistently reproduce only a fraction of the observed low frequency variability, even when multiple models and multiple ensemble members are considered.51 Although it is difficult to assess the significance of such results because the period of rapid NAO increase has been preselected from the observational record, this underestimation of multidecadal variability of the NAO in atmosphere-only (and coupled ocean–atmosphere52) model experiments is consistent with the weak reproduction of NAO variability in the signal-to-noise paradox.
Numerous other studies also show weak modelled signals in simulations of the atmospheric circulation in the Atlantic sector. The NAO-like response to the stratospheric quasi-biennial oscillation in winter appears to be underestimated in climate simulations17,53,54 as is the NAO-like response to tripolar Atlantic SST anomalies55,56 and the apparent response to Arctic sea ice perturbations.57
In summary, it appears that the signal-to-noise paradox has been present in atmospheric climate models for some time and it may occur across a wide range of timescales and in the Atlantic response to a wide range of phenomena.
A signal-to-noise paradox in the response to external climate forcing?
A first line of evidence for a signal-to-noise paradox in the climate response to external forcing comes from the simulated response to tropical volcanic eruptions. Analysis of historical climate data in post eruption winters again suggests a response in sea level pressure that projects strongly on to the winter Arctic Oscillation or NAO,58,59 see Fig. 4, left panel.
Evidence for a signal-to-noise paradox in the response to volcanic forcing. Winter sea level pressure response to volcanic eruptions in CMIP5 models. Modelled responses (right) are several times smaller than observed responses (left). Note the order of magnitude difference in scale61
However, when volcanic aerosol forcing is added to climate models, the response in the AO or NAO is of the correct sign but invariably weak (Fig. 4, noting the different scale bars) and much weaker than observed for both multimodel and individual model studies.59,60,61,62 For example, Stenchikov et al.59 state that: “…associated dynamic perturbations and winter surface warming over Northern Europe and Asia in the post-volcano winters is much weaker in the models than in observations”. Furthermore, it has also been shown that the observed response appears to be too large to be easily reconciled as chance aliasing of internal variability of the Arctic Oscillation onto post volcanic winters.60,62,63 In contrast, the mean global cooling response to volcanic eruptions in climate models does not show this feature and may even be too strong,64,65 so it is likely that in this case, the global irradiance forcing is sufficient and it is again the regional response in the north Atlantic that appears to lack amplitude. Several studies also point out a prolonged response to volcanic forcing, with a second winter response that is similar to that in the winter immediately following the eruption58 but this lagged response is not generally reproduced in climate models either.59,62 The weak model response in the two winters following explosive tropical volcanic eruptions may therefore be another example of the signal-to-noise paradox, with a similar pattern but weaker amplitude Atlantic sector response than is found in observations.
A second line of evidence for a signal-to noise paradox in the external response to climate forcing comes from a number of studies that point out that the surface response to solar variability may be too weak in climate model experiments.66,67,68 Recent modelling studies have confirmed a regional response in sea level pressure that maps onto the Arctic Oscillation and NAO,67,69,70 as has previously been repeatedly suggested from analysis of historical climate observations.71,72,73 A connection with the signal-to-noise paradox described here comes from the observed response to the 11-year solar cycle reaching its maximum not at the peak of the solar cycle, but rather at a lag of a few (2–4) years.69,74 In climate model experiments,69 the transient response to a step change in solar forcing, grows year on year in association with a growing tripolar anomaly in the North Atlantic sea surface temperature. This tripolar SST pattern is known to feed positively back onto the atmospheric circulation associated with the NAO,37,38,40,55,75 so the integrating effect of the ocean due to the relatively long decay time of oceanic anomalies and the annual re-emergence of the solar induced heat content anomaly in the Atlantic could give rise to a delay in the maximum response69,74 as shown in Fig. 5.
Evidence of a signal-to-noise paradox in the response to solar forcing. Sea level pressure anomalies are plotted at various lags from the peak of the 11-year solar cycle in historical observations (left) and climate model simulations (right). Note the lagged response in the observed case. After Gray et al.68
Viewing the solar cycle as a boundary condition with an 11-year sinusoidal period, and viewing the response as an ocean integrated (cosine) wave with the same period, then we expect a lag of π/2 radians (one quarter cycle) in the timing of the maximum response. This is approximately 3 years for the 11-year solar cycle, as observed. In contrast, when taken as a whole, the reported responses to the 11-year solar cycle in current climate models appear to be weak and most model simulations show no clear lag.68,70,74,76,77 Scaife et al.74 showed that this could result from too weak a feedback in the surface climate response to solar variability. We should of course note that the strength of observational estimates of solar irradiance variations continue to be refined78 and this uncertainty in forcing may contribute to uncertainty in the amplitude of the solar response in surface climate. Nevertheless, the existence of a lag in the observed response and the apparent difficulty in simulating this lag in climate models is additional evidence of a weak response of the atmospheric circulation in the north Atlantic sector to external forcing which is again consistent with the signal-to-noise paradox in climate predictions.
Our last example of the possible effects of the signal-to-noise paradox is in the tropospheric climate response to the development of the ozone hole. While some studies report successful simulation of the temporal evolution,79 a number of studies have noted a weaker then observed response in the Southern Annular Mode (SAM)80,81,82,83 which is often then attributed to coincidental internal variability. While this coincidental alignment of forced and internal variability in the SAM is perfectly possible, we again note that the common tendency for models to simulate weaker than observed changes is consistent with a signal-to-noise paradox in the forced response of the SAM in models. Indeed, this has recently been found in seasonal climate predictions of the SAM.33
In summary, the signal-to-noise paradox may therefore also apply to a range of responses to external forcing, including volcanic forcing, solar variability, and ozone depletion.
Implications
If the signal-to-noise ratio is underestimated by climate model simulations and predictions, then each model ensemble member cannot be regarded as an equivalent realisation of the real climate system to that seen in the observations as it contains a smaller proportion of predictable variance than the observations. This has a number of important implications:
-
1.
Many measures will give inaccurate estimates of the forecast skill that is potentially available. These include error measures such as root-mean-squared error and mean-squared-skill-score,84 as well as probabilistic measures, including reliability and Brier skill score, that are based on the distribution of ensemble members.30 Errors in the signal-to-noise ratio can be corrected in forecasts by a postprocessing step that amplifies the predictable signal20,85 but measures that assess the raw model data without such a correction will be misleading. Note that anomaly correlation is not affected by the magnitude of the ensemble mean signal and is therefore unaffected, so it should be routinely included in any skill assessment, providing that a large enough ensemble is used to accurately estimate the predictable (ensemble mean) signal.
-
2.
Seasonal forecasts of tropical regions are typically overconfident and their statistical properties may be improved by techniques such as stochastic physics86 that often increase the ensemble spread. However, such techniques could potentially exacerbate problems where the signal-to-noise ratio is too small and the models are under-confident.
-
3.
Predictability is often estimated from model ensembles, for example, by assessing the skill of predicting a single model member instead of the observations.87,88,89 This has often been regarded as an upper limit of the skill that could be achieved using a particular model90 because it mimics the situation in which each ensemble member is initialised with perfect observations. However, if the signal-to noise ratio were too large, then the additional predictability in the model ensembles would be an overestimate, rather than representing potential for future improvement. Similarly, if the modelled signal-to-noise ratio is too small, as found here, then the real world is more predictable than the model (Fig. 1) and this approach will underestimate the true predictability.
-
4.
Event attribution91,92 seeks to quantify the change in the probability of weather events due to human influences. One approach is to compare a large ensemble of model simulations driven by observed SSTs with another ensemble driven by counterfactual SSTs—obtained by removing the anthropogenic signal. This relies on the model correctly simulating the amplitude of the response to SSTs and will give incorrect results, especially in the North Atlantic sector, where the signal-to-noise ratio is too small.
-
5.
Large ensembles of model simulations suggest that natural internal variability is the major source of uncertainty in regional climate change projections over the coming decades.93 This approach relies on the models correctly responding to external forcing, including greenhouse gases, anthropogenic aerosols and ozone. If the signal-to-noise paradox also applies to the response to these forcing factors, then the role of internal variability will be overestimated by this technique.
-
6.
Although the signal-to-noise paradox highlights a potentially serious problem with climate models, its discovery helps to reveal that skilful forecasts are now possible for some phenomena, including the NAO,23 including some of the most extreme cases94 that were previously thought to be unpredictable.95 We note that a large ensemble is required in order to extract the maximum predictable signal (Fig. 1), and postprocessing is needed to boost its magnitude.20
-
7.
Resolving the signal-to-noise paradox and correcting it in climate models could increase the strength of the model response to a whole host of phenomena and would settle longstanding debates about whether various teleconnections are real. It would also enable smaller ensembles to be used for detection, attribution and prediction, and could increase the skill of climate forecasts and climate services.
Conclusions
We have provided a wide range of evidence for a ‘signal-to-noise paradox’ in climate science. The paradox lies in the fact that climate models are better able to predict observed climate variability than would be expected from their low signal-to-noise ratio. However, in many cases, the total amount of variability found in ensemble member simulations closely matches that found in observations, and so it is not just a simple case of models being too ‘noisy’ or containing too much variability. We instead conclude that the amplitude of predictable signals in response to boundary conditions or external forcing may be much too weak, especially in the Atlantic sector. This helps to explain why so many climate modelling studies show clear relationships between model and observations only after anomalies are ‘standardised’. These anomalously weak signals in predictions hamper the use of seasonal and decadal predictions, inhibit the validity of probabilistic and ensemble approaches and prevent the accurate estimation of forced climate variability in the Atlantic sector.
The signal-to-noise paradox appears to be ubiquitous across timescales: it appears on timescales of seasons20,23,24,25,36,38 years20,26,39 and multi-decades.43,50,51 It may even be present on multi-century timescales in the Atlantic sector as there is proxy observational evidence for negative NAO and associated European cooling in the Little Ice Age96,97 but numerous studies have noted only weak model responses in the NAO98 and associated temperatures.99
The signal-to-noise paradox also appears to be ubiquitous across different climate models, spanning many years of model development and using a wide variety of ensemble generation techniques.23,25,27,28,29,38,39,43,55
The signal-to-noise paradox appears to be robust across different experimental procedures. It appears as weak signals in ensemble forecasts20,23,25,26,28,36 in atmosphere-only simulations forced by prescribed ocean conditions29,38,39,51,55 and in models subjected to changes in radiative forcing.59,61,62,74,99
While this review cannot provide absolute proof, it summarises a growing body of evidence for a signal-to-noise paradox in initialised climate predictions. A chance alignment of unpredictable and predictable variability could in principle lead to an apparent paradox in this context but this is very unlikely.21 Instead we suggest evidence that it may arise from an underestimate in the strength of a wide variety of North Atlantic teleconnections in climate models. The reasons for this remain unclear but there are a number of obvious candidates including: lack of extratropical ocean–atmosphere coupling, weak eddy feedback in current resolution models, errors in remote teleconnections, or errors in parametrised processes such as atmospheric convection. Some of the further supporting evidence given here may eventually be explained by other means, but there is also evidence that the signal-to-noise paradox may be present in the modelled response of the Atlantic sector to external radiative forcing. We do not yet know whether it applies to the regional response to anthropogenic greenhouse gases, but of course that is an important question for future research, as it could imply large changes in regional climate that are currently unrepresented in climate model projections.
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Lorenz, E. N. Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141 (1963).
Lorenz, E. N. The predictability of a flow which possesses many scales of motion. Tellus 21, 289–307 (1969).
Epstein, E. S. Stochastic dynamic prediction. Tellus 21, 739–759 (1969).
Murphy, J. & Palmer, T. N. Experimental monthly long-range forecasts for the United Kingdom. Part II. A real-time long-range forecast by an ensemble of numerical integrations. Meteorol. Mag. 115, 337–349 (1986).
MacLachlan, C. et al. Global seasonal forecast system version 5 (GloSea5): a high-resolution seasonal forecast system. Q. J. R. Meteorol. Soc. 141, 1072–1084 (2015).
Lambert, S. & Boer, G. CMIP1 evaluation and intercomparison of coupled climate models. Clim. Dyn. 17, 83 (2001).
Slingo, J. & Palmer, T. Uncertainty in weather and climate prediction. Philos. Trans. R. Soc. A 369, 4751–4767 (2011).
Alessandri, A. et al. Evaluation of probabilistic quality and value of the ENSEMBLES multimodel seasonal forecasts: comparison with DEMETER. Mon. Weather Rev. 139, 581–607 (2011).
Weisheimer, A. & Palmer, T. On the reliability of seasonal climate forecasts. J. R. Soc. Interface 11, 20131162 (2014).
Mason, S. J. et al. The IRI seasonal climate prediction system and the 1997/98 El Niño event. Bull. Am. Meteor. Soc. 80, 1853–1873 (1999).
Simmons, A. J. & Hollingsworth, A. Some aspects of the improvement in skill of numerical weather prediction. Q. J. R. Meteorol. Soc. 128, 647–677 (2002).
Domeisen, D. I. V., Badin, G. & Koszalka, I. M. How predictable are the Arctic and North Atlantic oscillations? Exploring the variability and predictability of the northern hemisphere. J. Clim. 31, 997–1014 (2018).
Vitart, F. Madden-Julian oscillation prediction and teleconnections in the S2S database. Q. J. R. Meteorol. Soc. 143, 2210–2220 (2017).
Luo, J., Masson, S., Behera, S. K. & Yamagata, T. Extended ENSO predictions using a fully coupled ocean–atmosphere model. J. Clim. 21, 84–93 (2008).
Doblas-Reyes, F. J. et al. Initialized near-term regional climate change prediction. Nat. Commun. 4, 1715 (2013).
Hermanson, L. et al. Forecast cooling of the Atlantic subpolar gyre and associated impacts. Geophys. Res. Lett. 41, 5167–5174 (2014).
Scaife, A. A. et al. Predictability of the quasi-biennial oscillation and its northern winter teleconnection on seasonal to decadal timescales. Geophys. Res. Lett. 41, 1752–1758 (2014).
Smith, D. M., Scaife, A. A. & Kirtman, B. What is the current state of scientific knowledge with regard to seasonal and decadal forecasting? Environ. Res. Lett. 7, 015602 (2012).
Sun, C., Li, J. & Zhao, S. Remote influence of Atlantic multidecadal variability on Siberian warm season precipitation. Sci. Rep. 5, 16853 (2015).
Eade, R. et al. Do seasonal to decadal climate predictions underestimate the predictability of the real world? Geophys. Res. Lett. 41, 5620–5628 (2014).
Siegert, S. et al. A Bayesian framework for verification and recalibration of ensemble forecasts: how uncertain is NAO predictability? J. Clim. 29, 995–1012 (2016).
Riddle, E. E., Butler, A. H., Furtado, J. C., Cohen, J. L. & Kumar, A. CFSv2 ensemble prediction of the wintertime Arctic Oscillation. Clim. Dyn. 41, 1099–1116 (2013).
Scaife, A. A. et al. Skilful long range prediction of European and North American winters. Geophys. Res. Lett. 41, 2514–2519 (2014).
Kang, D. et al. Prediction of the Arctic oscillation in boreal winter by dynamical seasonal forecasting systems. Geophys. Res. Lett. 41, 3577–3585 (2014).
Stockdale, T. N., Molteni, F. & Ferranti, L. Atmospheric initial conditions and the predictability of the Arctic oscillation. Geophys. Res. Lett. 42, 1173–1179 (2015).
Dunstone, N. et al. Skilful predictions of the winter North Atlantic Oscillation one year ahead. Nat. Geosci. https://doi.org/10.1038/NGEO2824 (2016).
Athanasiadis, P. J. et al. A multisystem view of wintertime NAO seasonal predictions. J. Clim. 30, 1461–1475 (2017).
Saito, N., et al. Seasonal predictability of the North Atlantic Oscillation and zonal mean fields associated with stratospheric influence in JMA/MRI-CPS2. SOLA 13, 209–213 (2017).
Kumar A. & M. Chen. Causes of skill in seasonal predictions of the Arctic Oscillation. Clim. Dyn. https://doi.org/10.1007/s00382-017-4019-9 (2017).
Wilks, D. S. Statistical Methods in the Atmospheric Sciences 3rd edn (Academic Press, Oxford, Waltham, MA, 2011).
Shi, W., Schaller, N., MacLeod, D., Palmer, T. N. & Weisheimer, A. Impact of hindcast length on estimates of seasonal climate predictability. Geophys. Res. Lett. 42, 1554–1559 (2015).
Kumar, A., Peng, P. & Chen, M. Is there a relationship between ptential and actual skill? Mon. Weather Rev. 142, 2220–2227 (2014).
Seviour, W. J. et al. Skillful seasonal prediction of the Southern annular mode and Antarctic ozone. J. Clim. 27, 7462–7474 (2014).
Ho, C. K. et al. Examining reliability of seasonal to decadal sea surface temperature forecasts: The role of ensemble dispersion. Geophys. Res. Lett. 40, 5770–5775 (2013).
Sheen, K. L. et al. Skilful prediction of Sahel summer rainfall on inter-annual and multi-year timescales. Nat. Commun. 8, 14966 (2017).
Dunstone, N. J. et al. Skilful seasonal predictions of Summer European rainfall. Geophys. Res. Lett. https://doi.org/10.1002/2017GL076337 (2018).
Rodwell, M. J., Rowell, D. P. & Folland, C. K. Oceanic forcing of the wintertime North Atlantic Oscillation and European climate. Nature 398, 320–323 (1999).
Mehta, V. M., Suarez, M. J., Manganello, J. V. & Delworth, T. L. Oceanic influence on the North Atlantic Oscillation and associated northern hemisphere climate variations: 1959–1993. Geophys. Res. Lett. 27, 121–124 (2000).
Latif, M., Arpe, K. & Roeckner, E. Oceanic control of decadal North Atlantic sea level pressure variability in winter. Geophys. Res. Lett. 27, 727–730 (2000).
Visbeck, M., et al. in The North Atlantic Oscillation : Climate Significance and Environmental Impact. Eds Hurrell, J., Kushnir, Y., Ottersen, G. & Visbeck, M., American Geophysical Union Monograph. https://doi.org/10.1029/GM134 (2003)..
Bretherton, C. S. & Battisti, D. S. An interpretation of the results from atmospheric general circulation models forced by the time history of the observed sea surface temperature distribution. Geophys. Res. Lett. 27, 767–770 (2000).
Hanna, E., Cropper, T. E., Jones, P. D., Scaife, A. A. & Allan, R. Recent seasonal asymmetric changes in the NAO (a marked summer decline and increased winter variability) and associated changes in the AO and Greenland Blocking Index. Int. J. Climatol. 35, 2540–2554 (2015).
Hoerling, M. P. et al. Twentieth century North Atlantic climate change. Part II: Understanding the effect of Indian Ocean warming. Clim. Dyn. 23, 391 (2004).
Scaife, A. A., Knight, J. R., Vallis, G. K. & Folland, C. K. A stratospheric influence on the winter NAO and North Atlantic surface climate. Geophys. Res. Lett. 32, L18715 (2005).
Greatbatch, R. J., Gollan, G., Jung, T. & Kunz, T. Factors influencing Northern Hemisphere winter mean atmospheric circulation anomalies during the period 1960/61 to 2001/02. Q. J. R. Meteorol. Soc. 138, 1970–1982 (2012).
Kucharski, F., Molteni, F. & Bracco, A. Decadal interactions between the western tropical Pacific and the North Atlantic Oscillation. Clim. Dyn. 26, 79–91 (2005).
Semenov, V. A., Latif, M., Jungclaus, J. H. & Park, W. Is the observed NAO variability during the instrumental record unusual? Geophys. Res. Lett. 35, L11701 (2008).
Sun, C., Li, J. & Jin, F.-F. A delayed oscillator model for the quasi-periodic multidecadal variability of the NAO. Clim. Dyn. 45, 2083–2099 (2015).
Shindell, D. T., Schmidt, G. A., Miller, R. L. & Rind, D. Northern hemisphere winter climate response to greenhouse gas, ozone, solar, and volcanic forcing. J. Geophys. Res. 106(D7), 7193–7210 (2001).
Gillett, N. P., Zwiers, F. W., Weaver, A. J. & Stott, P. A. Detection of human influence on sea-level pressure. Nature 422, 292–294 (2003).
Scaife, A. A. et al. The CLIVAR C20C project: selected twentieth century climate events. Clim. Dyn. 33, 603–614 (2009).
Wang, X., Li, J., Sun, C. & Liu, T. NAO and its relationship with the Northern Hemisphere mean surface temperature in CMIP5 simulations. J. Geophys. Res. Atmos. 122, 4202–4227, https://doi.org/10.1002/2016JD025979.
Marshall, A. G. & Scaife, A. A. Impact of the QBO on surface winter climate. J. Geophys. Res. 114, D18110 (2009).
Anstey, J. A., Shepherd, T. G. & Scinocca, J. F. Influence of the quasi-biennial oscillation on the extratropical winter stratosphere in an stmospheric heneral virculation model and in reanalysis data. J. Atmos. Sci. 67, 1402–1419 (2010).
Rodwell, M. J. & Folland, C. K. Atlantic air–sea interaction and seasonal predictability. Q. J. R. Meteorol. Soc. 128, 1413–1443 (2002).
Gastineau, G., D’Andrea, F. & Frankignoul, C. Atmospheric response to the North Atlantic Ocean variability on seasonal to decadal time scales. Clim. Dyn. 40, 2311 (2013).
Mori, M., Watanabe, M., Shiogama, H., Inoue, J. & Kimoto, M. Robust Arctic sea-ice influence on the frequent Eurasian cold winters in past decades. Nat. Geosci. 7, 869–873 (2014).
Robock, A. & Mao, J. The volcanic signal in surface temperature observations. J. Clim. 8, 1086–1103 (1995).
Stenchikov, G. et al. Arctic Oscillation response to volcanic eruptions in the IPCC AR4 climate models. J. Geophys. Res. 111, D07107 (2006).
Marshall, A. G., Scaife, A. A. & Ineson, S. Enhanced seasonal prediction of European winter warming following volcanic eruptions. J. Clim. 22, 6168–6180 (2009).
Driscoll, S., Bozzo, A., Gray, L. J., Robock, A. & Stenchikov, G. Coupled Model Intercomparison Project 5 (CMIP5) simulations of climate following volcanic eruptions. J. Geophys. Res. 117, D17105 (2012).
Swingedouw, D. et al. Impact of explosive volcanic eruptions on the main climate variability modes. Glob. Planet. Change 150, 24–45 (2017).
Christiansen, B. Volcanic eruptions, large-scale modes in the Northern Hemisphere, and the El Niño-Southern Oscillation. J. Clim. 21, 910–922 (2008).
Schurer, A. P., Hegerl, G. C., Mann, M. E., Tett, S. F. B. & Phipps, S. J. Separating forced from chaotic climate variability over the past millennium. J. Clim. 26, 6954–6973 (2013).
Smith, D. M. et al. Role of volcanic and anthropogenic aerosols in recent slowdown in global surface warming. Nat. Clim. Change 6, 936–940 (2016).
Stott, P. A., Jones, G. S. & Mitchell, J. F. Do models underestimate the solar contribution to recent climate change? J. Clim. 16, 4079–4093 (2003).
Matthes, K., Langematz, U., Gray, L. L., Kodera, K. & Labitzke, K. Improved 11-year solar signal in the Freie Universität Berlin Climate Middle Atmosphere Model (FUB-CMAM). J. Geophys. Res. 109, D06101 (2004).
Gray, L. J. et al. A lagged response to the 11 year solar cycle in observed winterAtlantic/European weather patterns. J. Geophys. Res. Atmos. 118, 13,405–13,420 (2013).
Ineson, S. et al. Solar forcing of winter climate variability in the Northern Hemisphere. Nat. Geosci. 4, 753–757 (2011).
Thiéblemont, R., Matthes, K., Omrani, N.-E., Kodera, K. & Hansen, F. Solar forcing synchronizes decadal North Atlantic climate variability. Nat. Commun. 6, 8268 (2015).
Kodera, K. & Kuroda, Y. Dynamical response to the solar cycle. J. Geophys. Res. 107(D24), 4749 (2002).
Lockwood, M., Harrison, R. G., Woollings, T. & Solanki, S. K. Are cold winters in Europe associated with low solar activity? Environ. Res. Lett. 5, 024001 (2010).
Woollings, T., Lockwood, M., Masato, G., Bell, C. & Gray, L. Enhanced signature of solar variability in Eurasian winter climate. Geophys. Res. Lett. 37, L20805 (2010).
Scaife, A. A. et al. A mechanism for lagged North Atlantic climate response to solar variability. Geophys. Res. Lett. 40, https://doi.org/10.1002/grl.50099 (2013).
Yukimoto, S. & Kodera, K. Annular modes forced from the stratosphere and interactions with the ocean. J. Meteorol. Soc. Jpn. 85, 943–952 (2000).
Andrews, M. B., Knight, J. R. & Gray, L. J. A simulated lagged response of the North Atlantic Oscillation to the solar cycle over the period 1960–2009. Env. Res. Lett. 10, 5 (2015).
Misios, S. et al. Solar signals in CMIP-5 simulations: effects of atmosphere–ocean coupling. Q. J. R. Meteorol. Soc. 142, 928–941 (2016).
Matthes et al. Solar forcing for CMIP6 (v3.2). Geosci. Model Dev. 10, 2247–2302 (2016).
Thompson, D. W. J. et al. Signatures of the Antarctic ozone hole in Southern Hemisphere surface climate change. Nat. Geosci. 4, 741–749 (2011).
Karpechko, A. Y., Gillett, N. P., Marshall, G. J. & Scaife, A. A. Stratospheric influence on circulation changes in the Southern Hemisphere troposphere in coupled climate models. Geophys. Res. Lett. 35, L20806 (2008).
Dall’Amico, M. et al. Impact of stratospheric variability on tropospheric climate change. Clim. Dyn. 34, 399–417 (2010).
Morgenstern, O. et al. Direct and ozone-mediated forcing of the Southern Annular Mode by greenhouse gases. Geophys. Res. Lett. 41, 9050–9057 (2014).
Seviour, W. J., Waugh, D. W., Polvani, L. M., Correa, G. J. & Garfinkel, C. I. Robustness of the simulated tropospheric response to ozone depletion. J. Clim. 30, 2577–2585 (2017).
Goddard, L., et al. A verification framework for interannual-to-decadal predictions experiments. Clim. Dyn. https://doi.org/10.1007/s00382-012-1481-2 (2012).
Sansom, P. G., Ferro, C. A. T., Stephenson, D. B., Goddard, L. & Mason, S. J. Best practices for postprocessing ensemble climate forecasts. Part I: Selecting appropriate recalibration methods. J. Clim. 29, 7247 (2016).
Weisheimer, A., Palmer, T. N. & Doblas-Reyes, F. J. Assessment of representations of model uncertainty in monthly and seasonal forecast ensembles. Geophys. Res. Lett. 38, L16703 (2011).
Griffies, S. & Bryan, K. A predictability study of simulated North Atlantic multidecadal variability. Clim. Dyn. 13, 459–487 (1997).
Koenigk, T. & Mikolajewicz, U. Seasonal to interannual climate predictability in mid and high northern latitudes in a global coupled model. Clim. Dyn. 32, 783 (2009).
Branstator, G. & Teng, H. Two limits of initial-value decadal predictability in a CGCM. J. Clim. 23, 6292–6310 (2010).
Boer, G. J., Kharin, V. V. & Merryfield, W. J. Decadal predictability and forecast skill. Clim. Dyn. 41, 1817–1833 (2013).
Stott, P. A. et al. Attribution of extreme weather and climate-related events. WIREs Clim. Change 7, 23–41 (2016).
Schaller, N. et al. Human influence on climate in the 2014 southern England winter floods and their impacts. Nat. Clim. Change 6, 627–634 (2016).
Deser, C., Phillips, A., Bourdette, V. & Teng, H. Uncertainty in climate change projections: the role of internal variability. Clim. Dyn. 38, 527–547 (2012).
Fereday D., A. Maidens, A. Arribas, A.A. Scaife & J.R. Knight. Seasonal forecasts of Northern Hemisphere Winter 2009/10. Env. Res. Lett. 7, https://doi.org/10.1088/1748-9326/7/3/034031 (2012).
Jung, T., Vitart, F., Ferranti, L. & Morcrette, J.-J. Origin and predictability of the extreme negative NAO winter of 2009/10. Geophys. Res. Lett. 38, L07701 (2011).
Trouet, V. et al. Persistent positive North Atlantic Oscillation mode dominated the Medieval Climate Anomaly. Science 324, 78–80 (2009).
Leijonhufvud, L. et al. Five centuries of Stockholm winter/spring temperatures reconstructed from documentary evidence and instrumental observations. Clim. Change 101, 109–141 (2010).
Moreno-Chamarro, E., Zanchettin, D., Lohmann, K., Luterbacher, J. & Jungclaus, J. H. Winter amplification of the European Little Ice Age cooling by the subpolar gyre. Sci. Rep. 7, 9981 (2017).
Owens, M. J. et al. The Maunder minimum and the Little Ice Age: an update from recent reconstructions and climate simulations. J. Space Weather Space Clim. 2017, A33 (2017).
Acknowledgements
This work was supported by the Joint DECC/Defra Met Office Hadley Centre Climate Programme (GA01101).
Author information
Authors and Affiliations
Contributions
Both authors researched, collated and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Scaife, A.A., Smith, D. A signal-to-noise paradox in climate science. npj Clim Atmos Sci 1, 28 (2018). https://doi.org/10.1038/s41612-018-0038-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41612-018-0038-4
This article is cited by
-
Northern Hemisphere winter atmospheric teleconnections are intensified by extratropical ocean-atmosphere coupling
Communications Earth & Environment (2024)
-
Contributions of external forcing and internal variability to the multidecadal warming rate of East Asia in the present and future climate
npj Climate and Atmospheric Science (2024)
-
Winter precipitation predictability in Central Southwest Asia and its representation in seasonal forecast systems
npj Climate and Atmospheric Science (2024)
-
Will the Globe Encounter the Warmest Winter after the Hottest Summer in 2023?
Advances in Atmospheric Sciences (2024)
-
SPEEDY-NEMO: performance and applications of a fully-coupled intermediate-complexity climate model
Climate Dynamics (2024)