Introduction

The gravitational pull of the moon excites tidal variations in atmospheric circulation with L2 frequency (period ~12.42 h). These variations are small—typically an order of magnitude less than solar diurnal and semidiurnal variations (which are forced primarily by the daily cycle of solar heating).1,2 However the lunar tide is singular as a purely mechanically (i.e., adiabatically) forced monochromatic (i.e., single frequency) variation and so observations of the L2 tide can provide uniquely valuable diagnostics of atmospheric behavior that enhance understanding of the atmospheric circulation. A historically important example is provided by long-standing observations of L2 variations in surface geomagnetic field that have informed our understanding of the ionospheric dynamo and upper atmospheric winds.3 Very recently it has been demonstrated that the L2 circulation variations in the troposphere modulate tropical rainfall,4 and the measurements of the L2 rainfall variation provide a valuable constraint on the representation of moist convective processes in climate models.5

In this study, we focus on measurements of the L2 tide in surface air and show that the results provide important information on the thermal coupling of the atmosphere with the underlying surface. The L2 variation in surface air pressure, L2(p), has been reliably determined at many stations where very long records of hourly measurements are available and its geographical and seasonal dependence have been established1,6,7,8 (Supplementary discussion for a brief review). The basic features of the observed L2(p) have been reproduced by simplified linear theory calculations of the response of the global atmosphere to the lunar gravitational forcing.2,9,10 The L2 surface air temperature cycle, L2(T), is expected to have an amplitude ~0.01 K making it quite hard to detect among all the other atmospheric disturbances present. The only direct observational report so far was obtained at a single location, Batavia (6°S, 106.5°E), by Chapman11 using hourly data during 1866–1928 and this determination had large uncertainty due to sampling noise (Note that a recent study4 estimated the size of the troposphere-average L2(T) based on global reanalysis model data). In this study, we analyzed long data records at many ocean buoys to determine accurate values of L2(T) over the tropical ocean.

The L2 forcing will excite a linear wave response in the atmosphere whose air temperature perturbations near the surface (\(\hat T\): complex amplitude) are governed by

$$\hat T = \frac{{i\omega }}{{i\omega + \beta }}\hat T_{{\rm ad}},$$
(1)

where ω is he frequency (=2π/12.42 h−1), and \(\hat T_{{\rm ad}}\) is the adiabatic component defined as,

$$\hat T_{ad} \equiv \frac{{R\bar T}}{{C_p\bar p}}\hat p,$$
(2)

where \(\hat p\) is the complex amplitude of L2(p) (see Methods section for details). Because there is no “external” thermal forcing for L2, the diabatic heating is expressed here as an effective Newtonian cooling with rate, β. Chapman12 suggested that (over land at least) L2(T) should to first order be in adiabatic relationship with L2(p), with deviations from this purely adiabatic behavior serving as a diagnostic of damping of the temperature signal in the air near ground (which he suggested would be dominated by heat exchange with the underlying surface). Chapman’s single-station determination11 indeed showed a first order adiabatic relation between L2(T) and L2(p) but was not sufficiently precise to reliably determine the strength of any thermodynamic damping. Curiously Chapman12 also suggested that air-sea coupling would be so strong that “over the oceans the lunar atmospheric tide will appear to be isothermal at sea level”. Our results will contradict this last assertion but will show that Chapman’s idea of using determinations of L2(T) and L2(p) to infer damping rates can be useful if enough data are analyzed.

Note that for a propagating wave phenomenon such as the lunar tide, the thermodynamic “damping” effects, through either radiative transfer or sensible heat fluxes, will depend not just on the local T′ but also on the T′ in other layers of the atmosphere, and so the β in (1) may be complex13,14 (the real part of β must be positive, of course). In addition there is the possibility of an L2 signal in latent heat release, although that is expected to be small in the (generally cloud/fog free15) air just above the tropical ocean.

Results: analysis of buoy data

We have for the first time detected L2(T) over ocean by using data from dozens of moored buoy stations across the tropical Pacific and Atlantic. The observed 12-h harmonic determined from data during any day (S2-obs) results from the superposition of true solar semidiurnal tide (S2) and the L2 that is dependent on the lunar phase (ν)2, that is,

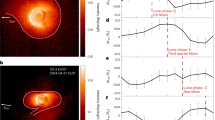
$$\begin{array}{*{20}{l}}S_{2 - {\rm obs}}(\nu ) & = S_2 + L_2(\nu )\\ & = s_2\cos \left( {\omega \left( {t_{LT} - \phi _2} \right)} \right) + l_2\cos \left( {\omega \left( {\tau - \lambda _2} \right)} \right)\\ & = s_2\cos \left( {\omega \left( {t_{LT} - \phi _2} \right)} \right) + l_2\cos \left( {\omega \left( {t_{LT} - \lambda _2} \right) - \nu \pi /6} \right)\cr \end{array},$$
(3)

where t LT is mean local solar time (MLST in h), s 2 and φ 2 are amplitude and phase of S2, τ is mean local lunar time (MLLT in h), l 2 and λ 2 are amplitude and phase of L2, and ω = 2π/12 (h−1). Here ν is an integer, increasing from 0 to 11 twice in each lunation (new moon to full moon and full moon to new moon) The relation, tLT = τ + ν + 12n (n: integer), is used for the transformation.2 Figure 1 shows the S2-obs and the anomaly from the average over the lunar phase at the buoy at (0°N, 220°E) (panels a, b), as well as the results averaged over the 38 stations (panels c, d). Obviously the true S2, the component independent of ν, is dominant (~0.05 K; Fig. 1a, c); however, the anomaly from S2 (~0.01 K) clearly shows the lunar phase progression (Fig. 1b, d), indicating a significant L2 signal even for single-station data. The temperature maximum of L2 is observed around at 10:00 MLLT regardless of ν (see Methods section for details about the procedure for determining the amplitude and phase of L2). The effects of beating between the true S2 and L2 signals appears as a modulation of the amplitude for the observed S2 ​from maximum (spring tide) around ν = 10 to minimum (neap tide) around ν = 4 (Fig. 1a, c).

Fig. 1
figure 1

a Semidiurnal harmonic of temperature observed at (0°N, 220°E) as functions of mean local solar time (MLST) and lunar phase (0 is new/full moon and 6 is half-moon). b As is (a) but for the anomaly from the mean S2 variation (computed as the average over the lunar phase). The mean local lunar time (MLLT) is shown by magenta lines. c, d are as (a–b) but for the results averaged over the 38 buoy stations

Full size image

Figure 2a shows the observed L2(T) (red arrows) and L2(p) (blue arrows) over the tropical Pacific and Atlantic, as well as the uniform-grid L2(p) product developed by Schindelegger and Dobslaw8 (SD16). The results are presented as harmonic dial vectors showing the amplitude and MLLT phase. L2(p) are converted to corresponding adiabatic temperature tide (referred to as L2(Tad)) using Eq. (2). L2(T) has a coherent structure with the phase at most stations being 10:00–12:00 MLLT. At the same time, a systematic geographical dependence is also obvious, particularly in the zonal direction; for example, both L2(T) and L2(Tad) are stronger at ~180°E and ~220°E compared to ~200°E. Figure 2b shows the scatter plot of L2(T) and L2(Tad) at selected longitudes. It is seen that generally the amplitude of L2(T) is slightly smaller than that of L2(Tad), with the phase of L2(T) earlier than that of L2(Tad). This is consistent with a basic picture of an adiabatically forced mechanical wave slightly modified by thermal damping processes.

Fig. 2
figure 2

a Horizontal distribution of harmonic dial vectors over the tropical Pacific and Atlantic ocean for (red) L2(T) from temperature measurements (38 stations), (blue) L2(Tad) from pressure measurements (7 stations), and (light-blue) L2(Tad) from grid dataset by SD16. b–f As (a) but for selected longitudes; only the end points of harmonic dial vectors plotted with the error bars

Full size image

Figure 3 shows the L2(T) (from buoys) and L2(Tad) (from both buoys and the SD16 grid data), plotting all values. The mean amplitude and phase of L2(T) are ~0.007 K and ~11:20 am/pm MLLT, respectively. It is clearly seen that the L2(T) amplitude is smaller than that of L2(Tad) and that L2(T) precedes L 2 (Tad) by ~20 min. The spread among the stations reflects the geophysical distribution of L2 signals (Fig. 2b), as well as observational uncertainty.

Fig. 3
figure 3

a Harmonic dial of (red circles) L2(T) and (blue circles) L2(Tad) from buoy measurements (38 selected stations for L2(T); 7 stations for L2(Tad)). The results from stations east of 160°E, where both L2(T) and L2(Tad) are determined (Fig. 2), are shown. The size of each circle denotes the number of days used for the analysis. Horizontal and vertical bars for each datum denote 95% confidence level with t-test (Methods section). Light-blue open circles are from the grid L2(Tad) data by SD16 for each location of L2(T) measurements. Solid and dashed arrows denote the average harmonic dial vectors for L2(T) from buoys and L2(Tad) from SD16. b Two arrows are adopted by those in a. Red curve starting from the averaged L2(Tad) (dashed black arrow) toward zero indicates the values that L2(T) should take if β, the coefficient of damping, is allowed to take a real, positive value (red circles show the L2(T) for selected βr values)

Full size image

The systematic difference between L2(T) and L2(Tad) indicates the existence of damping processes exerted on L2 near the surface. The least-square estimation of β in Eq. (1) from buoy measurements (Methods section) shows that β ~ 6 × 10−5 exp (iπ/4), consisting of not only a real part (β r ) but also a significant imaginary part (β i ) (Fig. 3b). β r −1 is ~0.3 day, which is much shorter than estimates of the purely radiative damping timescale (~2 weeks) and also than the convective damping scale (1–10 days) in the tropical free troposphere.16,17

Discussion: Numerical Model Simulations

Following Sakazaki et al.5 we have run a version of a realistic near-global climate simulation model with all diurnal variations of solar radiative heating of the troposphere or surface suppressed (the “Remote-F experiment”, Methods section). In Remote-F the daily cycle of stratospheric heating excites a solar semidiurnal (S2) tide which propagates into the troposphere. For the atmosphere just above the tropical ocean surface this produces a situation very analogous to that of the L2 tide – a zonal wave 2 westward-traveling pressure wave with period 12 h (vs 12.42 h for L2) and no local diabatic effects except for those caused by the local longwave radiative damping and sensible heat exchange with the surface (plus any small latent heat release in the air directly above the tropical ocean surface). The same type of experiment was used to investigate the stratospheric role in diurnal cycles in precipitation and in surface pressure solar tides.5,18 In this configuration, the model was integrated for 12.5 months (15/11/1999–30/11/2000) and the results from the final 12 months of data were analyzed. Sakazaki et al.5 showed that the overall simulation including seasonal mean tropical rainfall is not strongly affected by the suppression of the tropospheric diurnal solar forcing. To examine the effect of air-sea interaction processes, the Remote-F integration was repeated three more times with the standard surface heat exchange coefficients in the model (CH) multiplied by factors (i) 0.5, (ii) 1.5, and (iii) 2.

Figure 4a–d shows the scatter plots of S2(T) and the S2(Tad) at the surface for the individual experiments with different CH. Obviously the forcing for the S2 tide in the model (stratospheric heating) differs from the gravitational forcing of the L2 tide in the real world and so we focus only on the relationship between S2(T) and S2(Tad). All experiments show that the amplitude of S2(T) is slightly smaller than that of S2(Tad), while the phase of S2(T) is 10–20 min earlier than S2(Tad). These characteristics are quite consistent with our buoy observations of L2. At the same time, it is obvious that the difference between S2(T) and S2(Tad) increases, both in amplitude and phase, with increasing CH. This suggests that the thermal interaction between air and sea is largely responsible for the damping process near the surface for a dynamical wave like L2 tide.

Fig. 4
figure 4

a–d As is Fig. 3a but for Remote-F model experiments with the CH value relative to the standard values of (a) 50%, (b) 100%, (c) 150%, and (a) 200%. Red and blue dots show the results of S2(T) and S2(Tad); in the model, T is temperature output at 2 m and Tad is calculated by using surface pressure. Only grid points over the tropical Pacific (10°S–10°N; 160°–270°E) and Atlantic (10°S–10°N; 330°–350°E) are used for analysis. See Fig. S6 for a different version in which red dots are plotted on top of the blue dots. e–h Frequency distribution of β ( = βr + iβi) from the four model experiments for the tropical Pacific and Atlantic. Blue dots with the error bar shows the estimated β from L2 observed by buoys

Full size image

Figure 4e–h shows the histograms of β ( = β r  + iβ i ), over the Pacific and Atlantic oceans, estimated for each experiment. Notably, not only the real part but also the imaginary part has a significant contribution in every experiment. Through all experiments, β may be reasonably approximated by, β = B exp (iπ/4), where B is the amplitude; but B increases with increasing CH, while the phase remains ~iπ/4. The phase lag agrees well with our L2 buoy measurements, while B best fits in the observed results in case of CH is increased by 50–100% over the standard value used in this model in earlier climate simulations (including studies with domains extending over tropical oceans19,20) (Fig. 4g, h). The sensitivity of β to CH found in our model shows that our L2 results can be a practical constraint for the parameterization of near-surface-process in climate models.

Supplementary Information includes a discussion of the heat budget over the S2 cycle in our Remote-F model experiments. Note, we can construct heat budgets only at the numerical model levels with the lowest located ~25 m above the surface (while the 2 m temperature is computed using similarity theory, Methods section). At altitudes <500 m, the S2 diabatic heating in Remote-F experiment comes largely from parameterized vertical diffusion processes (i.e., the vertical convergence of vertical sensible heat flux (τ): −dτ/dz) (Figs. S3 and S4). At the lowest model level (~25 m) (and presumably also nearer the surface) the phase of −dτ/dz precedes –T′ by 1–2 h (~π/4 for L2 and S2), consistent with the estimated β. We further find that the phase of −dτ/dz shows an upward progression with altitude, indicating that it takes a finite time for the heat to be transferred upward (Fig. S4). By contrast, τ itself is found to be in phase with −T′ (Fig. S2) at the surface (τ s ), indicating that τ s varies as a response to local T′ near the surface. These findings suggest that the damping on dynamical wave near the surface is largely caused by the vertical convergence of upward-propagating sensible heat flux that was injected from the surface due to the air-sea interaction (proportional to –T′). A simple analytical model predicts that the phase lag between the diabatic heating and −T′ near the surface should be between 0 and π/2 (Fig. S5 and Supplementary Information).

We have observed the L2 variation of surface air temperature at multiple locations, allowing us to now clearly determine these key features of L2 at low-latitudes: (i) L2(T) is to first order a moon-synchronous signal with T′ peaking around local lunar noon, (ii) the lunar temperature perturbations are roughly in adiabatic balance with the lunar pressure perturbations, but (iii) there is a clear indication of diabatic damping of the lunar temperature signal. We performed climate model experiments, including a close analogue of the L2 tide, by suppressing the daily solar heating cycle in the troposphere; the model results are consistent with our L2 observations when reasonable air-sea thermal coupling is included. This experiment is easy to perform and could be the focus for climate model intercomparisons to diagnose air-sea coupling.

Methods

Derivation of Equations (1)–(2)

We apply the thermodynamic equation for L2(T) observed just above (3 m) the ocean surface. Vertical winds can be ignored, while any effects of mean horizontal advection are also expected to be small as the horizontal phase speed of the tide is much larger than the mean winds near the surface. The equation can be thus written as,

$$\frac{{\partial T{\prime}}}{{\partial t}} = \frac{{R\bar T}}{{C_p\bar p}}\frac{{\partial p{\prime}}}{{\partial t}} + \dot Q \to \frac{{\partial T{\prime}}}{{\partial t}} = \frac{{R\bar T}}{{C_p\bar p}}\frac{{\partial p{\prime}}}{{\partial t}} - \beta T{\prime},$$
(4)

where t is time; \(\dot Q\) is L2 diabatic heating rate per unit mass (K s−1); T′ and p′ are L2(T) and L2(p), respectively; \(\bar T\) and \(\bar p\) are the mean state temperature and pressure, respectively; R is gas constant; Cp is specific heat of air. \(\dot Q\) is then represented by an effective Newtonian cooling with the coefficient, β. When we assume a simple harmonic solution with frequency ω (i.e., \(T{\prime} = \hat T\exp (i\omega t)\)and \(p{\prime} = \hat p\exp (i\omega t)\)), Equations (1) and (2) are obtained.

Analysis of Moored Buoy data

We analyze data from moored buoy arrays across the tropical Pacific and Atlantic oceans: the Tropical Atmosphere Ocean/Triangle Trans-Ocean Buoy Network (TAO/TRITON21) and the Prediction and Research Moored Array in the Atlantic (PIRATA22), respectively. Since early 1990s, these arrayed buoys have been observing the air temperature and pressure at 3 m above sea level with a high-temporal resolution (10 min to 1 h for temperature; 1 h for pressure). The resolution of temperature measurements is 0.01 K with their accuracy being 0.2 K, while that of pressure measurements is 0.1 hPa with their accuracy being 0.01%. For temperature, we show the L2 results obtained with only 10-min data (from ~1996 to September 2017) (temperature data from TRITON over the western Pacific (west to 160°E), whose resolution is 1-h, were not used for this study). For pressure, we show the results with hourly data up to September 2017 (there are no 10-min data for pressure). Figure S1 shows the data availability of 10-min temperature data for each buoy over the entire period up to September 2017. Although there are several data gaps, the measurements have continued over the last two decades.

Data are processed following the so-called Chapman-Miller (C-M) method2,23 except that we have employed an extensive quality control in advance to reduce the noise level as described below. First, we pick up days in which more than 60% are filled with valid data; for temperature (surface pressure) only the stations with the number of days meeting this criteria >4000 (>1500) are used for analysis (the criteria for pressure is weaker than that for temperature because the noise level is smaller). For each day (i.e., for 24-h time series), we applied a median-filter three times to eliminate the outliers such that any data outside of 3-sigma level from the median are considered as outliers (the median is calculated within each day with N-10 data, with N is the total number of data in the day for every iteration). Finally, the harmonic analysis is performed to extract the S2 component. The coefficients for the S2 cosine and sine curves are binned for each lunar phase (ν: integer from 0 to 11, where 0 (6) corresponds to the new/full moon (the half-moon)). Of all binned data for each ν, 50% around the median in each ν are used for further analysis.

The following calculation is based on the C-M method that will be briefly explained here. Let A2(ν) and B2(ν) be the sum of cosine and sine coefficients, respectively, over binned data for each ν. The cosine and sine coefficients for lunar semidiurnal signals (l a and l b ) are obtained as,

$$l_a = \frac{1}{K}\mathop {\sum}\limits_{\nu = 0}^{11} {\left[ {A_2(\nu )\cos \frac{{\nu \pi }}{6} + B_2(\nu )\sin \frac{{\nu \pi }}{6} - A_2(\nu )\frac{{N_A}}{N} - B_2(\nu )\frac{{N_B}}{N}} \right]},$$
(5)
$$l_b = \frac{1}{K}\mathop {\sum}\limits_{\nu = 0}^{11} {\left[ {B_2(\nu )\cos \frac{{\nu \pi }}{6} - A_2(\nu )\sin \frac{{\nu \pi }}{6} - B_2(\nu )\frac{{N_A}}{N} + A_2(\nu )\frac{{N_B}}{N}} \right]},$$
(6)

where

$$N_A = \mathop {\sum}\limits_{\nu = 0}^{11} {N(\nu )\cos \frac{{\nu \pi }}{6}} ,\,\,\,\,\,N_B = \mathop {\sum}\limits_{\nu = 0}^{11} {N(\nu )\sin \frac{{\nu \pi }}{6}} ,\,\,\,N = \mathop {\sum}\limits_{\nu = 0}^{11} {N(\nu )},$$
(7)
$$K = N\left\{ {1 - \left( {\frac{{N_A}}{N}} \right)^2 - \left( {\frac{{N_B}}{N}} \right)^2} \right\}.$$
(8)

Here, the third and fourth terms of Equations (5)–(6) are the correction terms taking into account any non-uniform distribution of days with respect to the lunar phase (v). The amplitude and phase of L2 (l2 and λ2, respectively, in Eq. (3)) are thus derived as,

$$l_2 = \sqrt {l_a^2 + l_b^2} ,\,\lambda _2 = \frac{6}{\pi }\tan ^{ - 1}l_b/l_a\left( {{\mathrm{MLLT}}} \right).$$
(9)

On the other hand, the cosine and sine coefficients of S2 (s a and s b ) are obtained by

$$s_a = \mathop {\sum}\limits_{\nu = 0}^{11} {\frac{{A_2(\nu )}}{{N(\nu )}},\,\,\,} s_b = \mathop {\sum}\limits_{\nu = 0}^{11} {\frac{{B_2(\nu )}}{{N(\nu )}}\,\,\,}$$
(10)

The S2 amplitude (s2) and phase (φ2) are thus

$$s_2 = \sqrt {s_a^2 + s_b^2} ,\,\phi _2 = \frac{6}{\pi }\tan ^{ - 1}s_b/s_a\left( {{\mathrm{MLST}}} \right)$$
(11)

The associated errors are estimated in the following procedure. We assume that for each day (i-th day), the observed S2 component can be actually expressed as

$$\begin{array}{*{20}{l}} S^i_{2 - {\rm obs}}(\nu ) & = s_{2 - {\rm obs}}^i\cos \omega t + s_{2 - obs}^i\sin \omega t\\ & = S_2 + L_2(\nu ) + \varepsilon _2^i\\ & = \left( {s_a\cos \omega t + s_b\sin \omega t} \right) + \left( l_a\cos \left( {\omega t - \nu \pi /6} \right)\right.\\ &\quad \left. + l_b\sin \left( {\omega t - \nu \pi /6} \right) \right) + \left( {\varepsilon _a^i\cos \omega t + \varepsilon _b^i\sin \omega t} \right) \end{array},$$
(12)

where the first term is the “true” S2 independent of lunar phase; the second term is the L2; the third term is the error. Now that we have obtained S2 (Eq. 11) and L2 (Eqs. 5–6), εi a and εi b are calculated for every day; then the errors on the harmonic dial are calculated as

$$E = \sqrt {\frac{1}{N}\mathop {\sum}\limits_i {\left( {\varepsilon _a^{i^2} + \varepsilon _b^{i^2}} \right)} } /\sqrt N$$
(13)

The error bars in Figs. 2 and 3 are defined as the 95% confidence levels for E with t-test (i.e., ~2E). For L2(T), we show the results at 38 stations with relatively small error bars (<0.0016 K; this limit is determined by trial-and-error).

Grid L 2 data from Schindelegger and Dobslaw (2016)

We use the global grid L2(p) dataset that was developed by Schindelegger and Dobslaw8 on the basis of 2315 selected ground-based measurements between 1900 and 2010 from land barometers and moored buoys (including TAO/TRITON and PIRATA used in this paper). It should be noted that they made a correction for the vertical displacement of buoy sensors due to oceanic L2 tides. Although such correction terms are non-negligible,24 we use data before the correction; these represent actual L2(p) determination in surface air (data were provided by M. Schindelegger, personal communication). For converting the L2(p) to L2(Tad) for this grid data, mean temperature and surface pressure (coefficients of Eq. 2) are derived from ERA-Interim reanalysis data for the period between 1998 and 2010.

Numerical simulations of L 2-like variations near the surface

We use a comprehensive limited-area atmospheric model developed at the International Pacific Research Center (IPRC) of University of Hawai’i at Manoa,19,20,25 which we run in near-global mode. Recently this model was used to study solar tides near the surface and their relationship with diurnal cycle in tropical rainfall.5,18

We do not directly simulate L2 signal (by adding the tidal potential to momentum equations26), but reproduce L2-‘like’ signals near the surface by running the model with the same configuration of “Remote-forcing (Remote-F) experiment” developed by Sakazaki et al.5 That is, the diurnal variation of solar heating in the troposphere and surface is eliminated by replacing the shortwave hearting and the shortwave flux at the surface with the daily-mean values on the same dates in a control run that was performed in advance. In this case, diurnal cycles near the surface are dominated by the S2 dynamical tide that is remotely excited in the stratosphere and propagates into the troposphere. Since there is no external, diabatic diurnal forcing near the ground and the frequency of S2 is close to that of L2, the S2 signal near the surface in Remote-F is a close analogue of L2.

The model is run in near-global zonal strip mode with SSTs and lateral boundary conditions at 75°S and 75°N specified from observational reanalyses. The integration is from 11/15/1999 to 11/30/2000; the 1-year data from 12/1/1999 to 11/30/2000 are used for the actual analysis. In order to examine the effect of heat exchange between air and surface on the L2(T)–L2(Tad) relationship, the Remote-F experiment was repeated with surface heat exchange coefficient (CH) changed by: (1) 50% decrease, (2) 50% increase, and (3) 100% increase.

Temperature at 2 m in altitude (T2m) in the model is calculated based on the similarity theory of the surface layer. Diabatic heating due to the vertical mixing processes near the surface are calculated using the Mellor–Yamada–Nakanishi–Niino scheme.27

Estimation of damping coefficient

By using the relationship between L2(T) and L2(Tad) for 38 buoy stations (L2(T) is from direct measurements while L2(Tad) is from SD16 data), the Newtonian cooling coefficient has been estimated. From Eq. (1), β is determined (\(\bar \beta\)) with the least-squares-method so that the following quantity, L, takes the minimum.

$$L = \mathop {\sum}\limits_n {\left| {\left( {i\omega + \bar \beta } \right)\hat T^n - i\omega \hat T_{{\rm ad}}^n} \right|} ^2,$$

where ω is the wave-frequency ( = 2π/12.42 h), \(\hat T^n\) and \(\hat T_{{\rm ad}}^n\) are the complex amplitudes of L2(T) and L2(Tad) at n-th station (e.g., \(L_2(T) = \hat T^n\exp (i\omega t)\)). The uncertainty of the estimated β is defined as

$$E = \sqrt {\frac{1}{{N_S}}\mathop {\sum}\limits_n {|\beta ^n - \bar \beta |^2} } /\sqrt {N_S},$$

where N s is the number of stations (38) and βn is determined for each station as,

$$\beta ^n = i\omega \left( {\frac{{\hat T_{{\rm ad}}^n}}{{\hat T^n}} - 1} \right).$$

The 95% confidence level (with t-test) is defined as 2E (t-value for the degree of freedom of 38 is 2).

Data availability

Buoy data can be obtained through the web site of the Pacific Marine Environmental Laboratory: https://www.pmel.noaa.gov/tao/drupal/disdel/. Model results will be publically available at the Asia-Pacific Data-Research Center (APDRC) at IPRC (http://apdrc.soest.hawaii.edu/).