Introduction

Although mathematics is often framed as objective and egalitarian, recognition of its elite is not equally conferred. Recent attention has been given to the Fields Medal, one of the most prestigious awards in math, and its elite community. When the award was first conceived in 1930, it was in part designed to elevate underrepresented mathematicians (Barany, 2018). The award was intentionally given to individuals that would otherwise not receive any recognition, rather than the best young mathematician. Although prizes can be seen as sources of elitism, the criteria for an award helps shape the definition of what elite means. The Fields Medal presents a case-study of a prize based on an expansive and equitable vision of scientific community. This study thus examines whether the Fields Medal succeeded, and if not, how it deviates from its original goal.

The production of science is a social and systemic endeavor, whose process has been analyzed across many dimensions (Merton, 1973). When observing the growth of publications within physics, Price observed the informal affiliation of scientists with common interests across distant colleges. Invisible colleges, as he called it, produced an elite who welded great respect within a discipline, and through this hierarchy generated bias of two primary types: citational and relational (de Solla Price, 1965).

Bias has been characterized in a few different ways. The Matthew Effect, addresses the over-representation of “top scholars” regardless of research similarity. The Matilda Effect refers to the systematic under-representation of female scientists (Rossiter, 1993). Most of these studies come out of sociology, and the work on prize giving and elitism is best exemplified by Harriet Zuckerman. In Zuckerman’s seminal Scientific elite: Nobel laureates in the United States, Zuckerman uses a database of 60,000 academics to illustrate the self-reinforcing attributes of America’s elite scientists (Zuckerman, 1977). Indeed, she provides fundamental notion of “accumulation of advantage” to describe how relative advantage is retained. In particular, she shows the Nobelists began their careers with the advantages of family support, a privileged education, early access to scientific equipment.

These sociological studies paved the way to our understanding of how identity—gender, language, and ethnicity—mediated the production of science. With the advent of the internet, digitization, and public data, the sociological approach has been augmented with network science. Within mathematics alone, several studies on elitism have been conducted. Methods draw predominantly from the complex network perspective (Zeng et al., 2017), leveraging network repositories such as citational networks. For instance, Ding finds collaboration between top scientists have increased from the 1990s onward. Beyond scholarship, studies have also considered hiring practices (Clauset et al., 2015) and departmental prestige (Myers et al., 2011).

We now take a closer look at mentorship and prize giving. Prior work has investigated the relationship between scientific mentorship and winning the Fields Medal or Wolf Prize. Rossi et al. studied the role of advisor–advisee relationships (Rossi et al., 2017) and proposed the genealogy index, adapted from the h-index which was initially developed by Hirsch (2005). While this showed the propagating effects of strong mentorship, its relationship to prize giving is tenuous. Gargiulo et al. studied the entire, connected giant component of the mathematical genealogy project (MGP), one of the most complete advisor–advisee databases maintained today. They further enriched the data using data mining techniques (Gargiulo et al., 2016). Their work focused on integrating math history with temporal network analysis, and provides a descriptive analysis of how fields in math evolved based on country, discipline, and the structure of academic genealogies. Malmgren et al. (2010) studied the role of mentorship on protégé performance, but focuses on metrics of academic success like publication record.

For prize-giving, Ma and Uzzi study how networks of different prize winners push the boundaries of science (Ma and Uzzi, 2018), and show a correlation between network structure and multiple prize-winning individuals. A similar study of self-reinforcing behavior has been conducted for the Nobel Prize (Wagner et al., 2015), motivated similarly as Zuckerman’s work but using contemporary network approaches. However, in both cases, collaboration (co-author) networks have been the focus, and ethnicity and gender identity has been unexplored.

A birds-eye view between mentorship, prize-giving, and ethnicity is thus desired, and the lack of metadata in these genealogies has limited the scope of investigation. However, as natural language processing (NLP) techniques have advanced, network science combined with lingo-ethnic classifiers may provide novel, albeit imperfect, insight towards how linguo-ethnic identity mediates the historical production of science.

In Zuckerman’s work, she does not indite the “accumulation of advantage” and work of Nobelists. Rather, she asks if limited access to elite status demonstrates a fundamental restriction to the democratic production of science. It is with a similar motivation we approach our study. In this paper, we analyze the flow of elite mathematicians between nations and lingo-ethnic categories, using social network analysis (SNA) and neural-based NLP. Like Gargiulo et al., analysis was performed on the Mathematics Genealogy Project (MGP), featuring more than 240,000 mathematicians, where we defined an elite circle formed around Fields Medalists. In the methods, we specify the details of our network construction, the classifiers used to enrich the database, and the critical measures we use to analyze our results.

Our analysis then demonstrates that while self-reinforcing behavior among the elites were present (congruous with the existing literature), it had also been used to elevate mathematicians of marginalized nationalities. The Fields Medal was part of a larger effort to integrate Japan after WWII. This is consistent with Parshall’s analysis of the Fields Medal, as part of a greater push to mend international relations, such as integrating Germany after World War II (Parshall, 2009). While we show increases in pluralism among major countries, Arabic, African, and East Asian identities remain under-represented at the elite level.

We conclude by discussing how concerted efforts by academic committees, such as prize giving, can either reinforce the existing elite or reshape its definition. A return to its roots, as Barany advocates, may provide just that. We anticipate our methodology of academic genealogical analysis can serve as a useful diagnostic for equity and systemic bias within academic fields.

Methods

Graph construction

The graph was constructed using the Mathematics Genealogy database (North Dakota State University, 2014). Nodes are mathematicians, and directed edges represent advisor–advisee relationships. The dataset contained information (listed in order of completeness) on the academic, advisor–advisee links, school, Ph.D. graduation year, country, and dissertation title and topic. The IDs of Fields Medalists were identified, and then the shortest path was computed in a pairwise fashion.

The subgroup of elites was thus created by taking the union of shortest paths between Fields Medalists. Our elite group is fully connected and denotes a minimal graph that connects all the medalists together. While it is possible to produce a minimal spanning tree, given the forest like structure of the genealogy, the shortest paths have more interpretative value. Analysis was conducted using the Networkx package (Hagberg et al., 2008).

 Table 1 shows a summary of key statistics from the dataset, including the number of mathematicians in each group. We have further made all code for analyses availableFootnote 1. Attribute data we use consisted of year of doctorate conferral, institution, and country of degree. These fields were mostly fully available for our set of elite mathematicians, and the handful of missing values we validated by hand.

Table 1 Summary statistics of the Mathematics Genealogy Project data set.
Full size table

Identity classifier

Since lingo-ethnic identity is not included in the Mathematics Genealogy Project, a separate classifier is required. The identity categories were labeled using the ethnicolr package, which is a long–short-term neural network (LSTM) trained on Wikipedia and the census (Sood and Laohaprapanon, 2018). LSTMs are the seminal work of Graves and Schmidhuber (Graves and Schmidhuber, 2005). This package has found use in evaluating under-representation in other STEM fields such as biomedicine (Marschke et al., 2018) and achieves between 78% and 81% accuracy. Potential shortcomings of neural methods for categorization is the accuracy levels. However, for 12 individual categories (which would result in 7.7% accuracy if truly random), 76% is significant. Additionally, since we are interested in comparison within individual demographics, any bias would be carried forward since the group of all mathematicians supersets the medalist subgroup and medalists themselves.

The goal of using this classifier is not to flatten definitions of identity, but to use the best available tools for inference, in the absence of concrete data. We use the Wikipedia-trained classifier specifically, leveraging its broader and more international training and validation set compared to the neural net trained on Census data.

Upon classifying a mathematician’s lingo-ethnic identity, we can measure their prominence by calculating the likelihood they win a Fields Medal. The power ratio (defined in Eq. (1)) is the conditional likelihood of being in the Fields Medalist Subgroup over the average probability of being in the group.

$${\rm {PR}}=\frac{P({\rm {Fields}}\,| \,{\rm {Institute}}\,\& \,{\rm {Identity}})}{P({\rm {Fields}})}.$$
(1)

Verbosely, this indicates the multiplying constant for a certain identity at an institution for winning the fields medal. We define top institutions as the top 50 most prominent institutions found within the elite community.

Flow analysis

To understand the interaction between groups, we aggregate mathematicians into their respective countries or ethnicities, and then analyze the flow between these meso-groups. By flow, we refer to the geographical and sociological implications of mentorship. For the case of countries, if a primary adviser received his doctorate in country A, then advised his advisee in country B, we know the adviser has moved between two countries. For lingo-ethnic identity, the notion of flow refers to how frequently members of different groups mentor students of the same or different lingo-ethnic identities.

Meso-graphs were constructed on attributes of each mathematician. To turn attributes into nodes, we constructed a mapping from mathematician to the meso-categories (lingo-ethnic identity and country where the doctoral degree was conferred). Edges between meso-categories are simply the original directed-edges between mathematicians. Each edge is then weighted by the number of advisor–advisee relations between meso-categories.

Constructing ternary diagrams

To visualize flow, we constructed ternary diagrams through analysis of the meso-network. Every meso-network can be represented by an adjacency matrix, which we denote M. The diagonal then accounts for self-flow, each columns excluding the diagonal element the in-flow, and rows excluding the diagonal elements the out-flow. Explicitly, for meso-category indexed by i, we have the following definitions for in-flow (IF), out-flow (OF), and self-flow (SF):

$$\begin{array}{lll}S{F}_{i}\,=\,{M}_{i,i}\\ \,I{F}_{i}\,=\,\mathop {\sum}\limits_{j\ne i}{M}_{j,i}\\ O{F}_{i}\,=\,\mathop {\sum}\limits_{j\ne i}{M}_{i,j}\end{array}$$

We then normalized these values to represent each meso-category as a point in three-dimensional space.

$${P}_{i}=\left(\frac{{\rm {I{F}}}_{i}}{{K}_{i}},\frac{{\rm {O{F}}}_{i}}{{K}_{i}},\frac{{\rm {S{F}}}_{i}}{{K}_{i}}\right)\in {[0,1]}^{3}\quad {\rm {with}}\ {K}_{i}={\rm {I{F}}}_{i}+{\rm {O{F}}}_{i}+{\rm {S{F}}}_{i}$$
(2)

Note, all points lie on the plane described by x + y + z = 1. We then transformed this planar section onto the two-dimensional plane using a translation and two rotations.

$$\begin{array}{lll}P^{\prime}={P}_{i}-(0,0,1),\\ P^{\prime\prime}={R}_{2}\circ {R}_{1}(P^{\prime} ),\end{array}$$
(3)

where R1 rotates the plane up to the XY-plane, and R2 aligns the simplex to the x-axis.

Results

Historical networks of elite migration

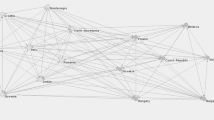
We begin with a sketch of history. Figure 1a captures the migration of elite mathematicians between five key countries impacted by significant migratory events, such as wars. Here, migration is determined by where advisors earned their Ph.D. and where their students earned their Ph.D. There are then two possibilities for what these links mean. First, a student moves abroad to study as part of their work, for which they establish a connection with their professor, before returning to their home country. Second, primary advisors move to the same country as their advisees. In both cases, we observe the migration of an elite mathematician while preserving directionality at the meso-level.

Fig. 1: Mobility patterns of mathematicians among countries (traditionally strong en mass).
figure 1

a The migration of elite mathematicians from 1800 to the present. b The net flow of elite mathematicians between 7 key countries. c The flow analysis of elite mathematicians between countries. Exporting means mathematicians flow out a country, importing means they flow in, and self-flowing means they are retained. Many countries only import at the elite level (etc., in the bottom right). A full list is available in the Supplementary Information.

Full size image

Prior to WWII, Western European countries were the strong-holds of mathematical thought. Notably, France and Germany contained the highest proportion of elite mathematicians. Japanese mathematicians studied in Germany, before returning to Japan, as part of modernization during the Meiji restoration. Examples include Teiji Takagi, who upon studying at the Imperial University of Tokyo was aided by David Hilbert. Prior to this, Rikitaro Fujisawa, who studied at the University of Strasbourg with Elwin Christofeel, returned (Chikara et al., 2013) and reformed mathematics education in Japan.

The flow chart reveals mass flows of researchers due to historical events. By 1932, the Holocaust led to mass migration from Germany to the United States and other European countries, which accounts for the drop in green volume in Fig. 1a, including prominent scientist Albert Einstein. Similarly, we observe large amounts of outflow from Russia after the cold war, greatly diminishing the presence of Russia mathematicians after the 1990s, and the second Italian mass diaspora after WWII. Beyond forced immigration, flow analysis also reveals the movement of reintegration. Japanese mathematicians immigrated to the United States following WWII, and continued throughout the 1960s to the 1990s. Twenty years later, Japanese mathematicians flowed back toward Japan.

France is not shown in the Sankey graph (Fig. 1a) as its purpose is to show historical migratory patterns, but is certainly historically one of, if not the most, influential countries in elite mathematics. The chord graph in Fig. 1b shows the net flow of mathematicians over all time, with the color of the chord indicating net exports. The USA-GER chord is orange, which indicates a net outflow from USA to Germany. Only France exports more to the States than it receives. In all others, the USA exports more to other countries. This seems to affirm France as the intellectual capital of mathematics.

Figure 1c shows the flow dynamics on a country level, again subset on only elite mathematicians as defined prior. In-flow is defined as the number of incoming edges, out-flow as the number of outgoing edge, and self-flow the number of loops. These results are similar to Gargiulo et al. (2016) with two striking differences. First, the United States has high self-flow and in-flow at the elite level, whereas in general it has high self-flow and out-flow. Secondly, there are many more importing countries compared to the general case, where most countries are exporting and self-flowing. Notice, many of the countries that are exporting and self-flowing are Western or part of the Soviet Union, where there were strong programs in mathematics. Other countries appear to import more at the elite level, because their “exports” are not as competitive as mathematicians exported from other countries.

We take a closer look at how the level of pluralism changes at the elite level in Fig. 2. Here, we associate each of these countries with the dominant identities—Germanic for German, Anglo for the United States, French for France, East Eurpoean for Russia, and Japanese for Japan. Panel (a) shows the proportion of elite minority groups within a time period. Panel (b) shows the number of elite mathematicians in each country, in raw amount.

Fig. 2: Upper-bounds of pluralism.
figure 2

Pluralism measure is defined by the proportion of elite mathematicians that are not part of the majority lingo-ethnic identity. a The proportion of elite minority groups within a time period. b The number of elite mathematicians in each country.

Full size image

We observe Germany, has consistently high levels of pluralism, save the period of WWII. On the other hand, in Japan, only recently has there been higher levels of non-Japanese elites within Japan. Pluralism in the United States has also increased over the years, as with the raw number of elite mathematicians. Russian elite mathematicians decrease significantly after the dissolution of the Soviet Union. To reiterate, our definition of elite is social, rather than some other measure of academic success such as the H-Index. This set of mathematicians bears elitism by virtue of their association with Fields Medalists.

Note, these serve lower bound for the level of pluralism—for instance, in the USA, individuals with anglo-phone names are common across different ethnicities. However, an audit of these names demonstrates consistency and has been included in the Supplementary Information. A sample is shown in Table 2.

Table 2 Inferred lingo-ethnic and country pairings of elite mathematicians from 1990 to the present.
Full size table

We note three things. First, in general, elite mathematicians have more mobility (in comparison with all mathematicians presented in Gargiulo et al. (2016)). Second, the United States imports more mathematicians as compared to the general case. In other words, while it exports net positive mathematicians overall, it attracts more elite members. Third, countries considered traditional math strong-holds tend toward the lower left corner of Fig. 1, demonstrating significant self-flow.

The flow of marginalized identities

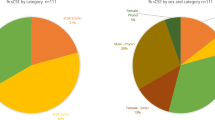
Upon analyzing the history of elite communities in mathematics, we turn to the present. As Fig. 1a shows, in the present, there is significant flow between countries. lingo-ethnic categories of identity serve as a useful construct for understanding network flow. Figure 3a shows the representation of identities, within three subgroups: all mathematicians (blue), mathematicians within the elite subgroup (green), and the Fields Medalists themselves (red). Figure 3 compares elite representation of subgroups relative to their actual proportions. There is a high proportion of French medalists (14%) compared to the general proportion (8%). In contrast, there is a significant number of East Asian mathematicians (14%) but very low representation in both the medalist community and medalists themselves (5% each). Further aggregation of groups are as follows. Greater European contains East Europe, Nordic, Germanic, Italian, Spanish, French, and Anglo. Asian includes Indian, East Asian, and Japanese. Greater African contains African and Arabic.

Fig. 3: Elite recognition and representation among lingo-ethnic identities.
figure 3

a The proportion of mathematicians within the elite community by identity. The three subgroups are: all mathematicians (blue), mathematicians within the medalist subgroup (green), and the medalists themselves (red). b Flow analysis by identity. Triangles denote the aggregate groups of lingo-ethnic categories.

Full size image

Groups where green and orange bars exceed blue bars indicate medalists and medalist families are over-represented, relative to the general population. In the opposite case, when green and orange are less than blue, then a group is under-representation. Over-represented groups include British, French, Japanese, East European, and Nordic names. Underrepresented groups include East Asian and Germanic. The Germanic under-representation would indicate that there is departure between mathematics and other applied and natural sciences, which Zuckerman observes. Specifically, divisions within European lingo-ethnic categories are also observed. Mathematicians with Arabic names are non-existent in Medalists and underrepresented in the elite community. As the Mathematics Genealogy Project may already include Western bias overall which would increase the baseline level of Western mathematicians, our representative analysis can be considered a conservative estimate.

On the level of flow, Fig. 3b characterizes identities in terms of in-flow, out-flow, and self-flow. High in-flow means a higher likelihood of being mentored. High out-flow then corresponds to a greater likelihood to mentor others. High self-flow means higher likelihood of mentoring your own identity. The identity with the most self-flow is Japanese. However, when all mathematicians are considered, the Japanese are shown as green, that is to say opposite of self-flowing. This indicates reinforcing behavior only occurs at elite levels. However, once these groups are aggregated into larger groups—Greater European, Asian, African, and Arabic—then differences become evident. European names has high self-reinforcing behavior, whereas Asians names and African and Arabic names are much lower in the number of self-loops. This dispels a common myth that minority groups, due to homophily, tend to group together.

Old strongholds, new possibilities

It is understandable that, when considering all mathematicians, there are high levels of self-flow—studying in elite and often foreign institutions is a privilege. However, high self-flow at the elite level may suggest institutions can do more to open access, given their greater access to resources. This has been the case for Japan. Japan is unique among Asian countries and identities in that there are many Japanese Fields Medalists (3), with high representation in elite levels. Japan has been known for its rapid westernization during the Meiji restoration relative to other Asian counterparts, and mathematics did not escape this trend either. Since 1872, their traditional form of math wasan was replaced by western science. Prussia, rather than the United Kingdom, was the primary source of westernization, and led directly to the establishment of the University of Tokyo (Parshall, 2009).

After WWII, mathematicians sought to re-establish international ties and formed the International Congress of Mathematicians and a new International Mathematics Union (IMU). Marshall Stone, a proponent of this movement, stated this clearly:

“...in considering American adherence to a Union, it must be borne in mind that we want nothing to do with an arrangement which excludes Germans and Japanese as such.” Indeed, we find the ten founding members well-represented in the ternary diagrams, and not long after founding, the Soviet Union joined. Revisiting Fig. 1a, we discover the density of elite mathematicians in Japan increases after 1945.

What the example of Japan says, as implied by its stature shown in Fig. 3, is the Fields Medal played a part in improving the status of marginalized populations. Mathematics historian Barany captures this aspiration, believing the fields medal should help “sculpt the future, rather than reward the past (Barany, 2018).” What we observe is the opposite, where the elite perpetuate the elite.

Figure 4 shows that all medalists can be traced to 9 connected components, with the largest one holding 44 out of 60 listed Medalists. This family is rooted from Gottfried Leibniz and Jean le Rond d’Alembert, who includes Laurent Schwartz, Simeon Denis Poisson, and David Hilbert.

Fig. 4: Ancestral tree by principle advisor for each fields medalist.
figure 4

Each red dot denotes a Fields Medalist.

Full size image

To give an example, within 5 generations after Schwartz, 7 Fields Medalists emerge. In particular, Schwartz–Grothendieck–Deligne form a direct chain, as do Lions–Villani–Figalli. Note, Lions’ father Jacque-Louis Lions was also a student of Schwartz. In other words, 13.3% of all Fields Medalists descended directly from Schwartz. Each of these all made contributions to some form of algebraic geometry or functional analysis.

Similar to Zuckerman’s analysis, these observations are not meant to diminish the achievements of great mathematicians. They do however, the importance of elite communities, and suggests the Fields Medal has deviated from its commitment to elevate under-represented mathematicians. Figure 5 shows this succinctly in a tabular heatmap, which shows the power ratios. To recap, the power ratio is the conditional likelihood of being in the Fields Medalist Subgroup over the average probability of being in the group (P = 0.00759).

$${\rm {PR}}=\frac{P({\rm {Fields}}\,| \,{\rm {Institute}}\,\& \,{\rm {Identity}})}{P({\rm {Fields}})}.$$
Fig. 5: The power ratio by identity.
figure 5

Elite circles is a strong indicator of recognition. The power ratio is the likelihood of being part of the elite community, divided by the average likelihood. It is a measure of relative likelihood.

Full size image

A mathematician that is French and attends a Top 50 institution means they are 6.4 times more likely to gain membership into the elite circle. Here, the top 50 is defined as the top institutions attended by those in the elite group. Note, we defined our Fields Medalist subgroup minimally, such that any other definition of subgroup would yield a higher power ratio. On the other hand, being East Asian and attending a Top 50 institution only affords you 1.5 times the likelihood of gaining membership into this elite circle.

From this diagram, we infer that institution plays a large role in elite membership. However, an East Asian mathematician from a top 50 school is 4.5 times less likely to be included than a French mathematician attending a top 50 school. An Indian mathematician educated outside top 50 schools are 6 times less likely to be included than a French mathematician with the same education. Amongst non-elite institutions, being Japanese gives the best chance of inclusion, an after-effect of the efforts by the IMU.

Conclusion

In 2014, the late Iranian mathematician Maryam Mirzakhani won the Fields Medal. A talented star, her groundbreaking work on dynamics and geometry was encouraged by her Ph.D. advisor Curtis McMullen, also a Fields Medalist, at the elite institution Harvard University. This is by no means downplaying her achievements; rather, it serves to show the power recognition and elite communities have—all of which membership she rightly earned. Although the Fields Medal should serve to recognize under-represented researchers, the proper cultivation of talent begins through mentorship and institutional support.

The purpose of the study was to revisit Zuckerman’s question of whether access to scientific elite circles had fundamental barriers, that would conflict with an equitable vision of scientific production. By focusing on the Fields Medal, once designed specifically to elevate under-represented mathematicians, we consider how it has fared historically and in the present day.

In our evaluation of the present, we find a large under-representation of minority groups in not just Field Medalists, but also in the elite circle for mathematics. While institutional prestige a big factor, lingo-ethnic identity is also found to be highly relevant, the widest gap being 4.5 times the power ratio even at elite institutions. Given that elite institutions have more resources, they can take a bigger role in generating higher access for marginalized groups. Flow analysis also dispels the common notion that under-representation arises from homophily driven self-selection.

Although the French stronghold shows the old forces that govern mathematical knowledge remain strong, the presence of Japanese scholars also shows concerted effort can be used as an integrating force. Concerted efforts by international academic committees, such as prize giving, are a powerful force to confer equal rights for knowledge production to traditionally marginalized groups.

While prizes can traditionally be understood as the very sources of elitism, the type of elitism varies by the criteria of conferral. The Fields Medal was special in its conception, as it aimed to bring attention to promising young scholars that were under-represented, those existed outside the established network. It drew a fine line between achievement, potential, and pre-existing elitism. In other words, it provided a vision of equality that recognized individuals to make them elite.

Rather it was supposed to. Our study shows, in hindsight, the elites of the Fields Medal produce a strong core of established mathematicians, with roots in a few specific countries and identities. The observation of Western bias is apparent, and mathematics, which touts itself as a universal language, does not escape this. By restricting the prize to those who have already become famous in their early career, the systemic biases inherent to academia are reinforced. Wealth is accumulated. We suggest two concluding points. First, elite institutions should continue to recruit from a diverse set of communities. Second, prizes that balance intellectual contribution, while simultaneously broadening community, would suit the vision of an equitable society that the Fields Medal once sought to do. Who is under-represented within a state shifts over geography, culture, and time. The vision of equitable scientific production demands constant evolution and reflection, especially at the elite level.