Abstract
Several micro-founded macroeconomic models with rational expectations address the issue of money emergence, by characterizing it as a coordination game. These models have in common the use of agents who dispose of perfect or near-perfect information on the global state of the economy and who display full-fledged computational abilities. Several experimental studies have shown that a simple trial-and-error learning process could constitute an explanation for how agents coordinate on a single mean of exchange. However, these studies provide subjects with full information regarding the state of the economy while restricting the number of goods in circulation to three. In this study, by the mean of multi-agent simulations and human experiments, we test the hypothesis according to which coordination over a unique medium of exchange is possible in the context of information scarcity. In our experimental design, subjects and artificial agents are only aware of the outcome of their own decisions. We provide results for economies with 3 and 4 goods to evaluate to which extent it is possible to generalize results obtained with 3 goods to \(n\) goods. Our findings show that in an economy à la Iwai, commodity money can emerge under drastic information restrictions with three goods in circulation, but generalization to four or more goods is not guaranteed.
Similar content being viewed by others
Introduction
In the last decades, monetary economics has shifted from a purely macroeconomic understanding of money to an analysis of its micro-foundations, both in its game-theoretical and behavioral dimensions. Following the intuitions of Karl Menger (1892) and starting with the Jones’ model in the mid-1970’s (Jones, 1976), several search-theoretic models have been proposed in order to identify the conditions for money emergence (Diamond, 1984; Kiyotaki and Wright, 1989, 1991; Oh, 1989; Aiyagari and Wallace, 1991; Kiyotaki and Wright, 1993; Shi, 1995; Iwai, 1996; Kehoe et al., 1993; Wright, 1995; Luo, 1998). They are considered search-theoretic models in the sense that they describe situations where agents need to search for a trading partner before transacting (Nosal and Rocheteau, 2011). Besides, these models belong to the class of micro-founded macroeconomic models with rational expectations. Agents with rational expectations can take advantage of all the available information to form their expectations and decide which action is optimal on the belief that every other agent in the economy has a similar ability (Muth, 1961).
Their first advantage is that they explain a macroeconomic phenomenon—money emergence—from individual decision-making processes. The second advantage of these models is that they explain money emergence that does not require the economies to be centralized: they do not need to assume a monetary authority for the agents to coordinate over a unique medium of exchange. Focusing on the function of a medium of exchange, these models highlight the key role that the money can play in limiting frictions in exchange processes (i.e., the difficulty to find an exchange partner). However, these models are based on three unrealistic assumptions: the omniscience of economic agents, infinite time and an extremely large number of agents (unbounded).
A question that immediately arises is whether money emergence without a monetary authority is possible in an economy populated by agents with restricted abilities and having limited access to information. More precisely, we want to know whether coordination over a unique medium of exchange is possible when agents proceed by trial and error and have access to local information only.
A partial answer has been brought to this question, through agent-based simulations with artificial agents using a reinforcement learning process (Marimon et al., 1990; Duffy and Ochs, 1999; Kindler et al., 2017) in a Kiyotaki-and-Wright’s environment (Kiyotaki and Wright, 1989, 1993). In these simulations, reinforcement learning agents have by construction limited computational abilities, and their informational inputs are only constituted by the success and failures of each exchange attempt. In contrast to Kiyotaki-and-Wright’s theoretical agents, they are completely blind to the global state of the economy, and the tuning of their preferences does not rely on the knowledge of the latter. Yet, results report achievement of monetary equilibria, indicating that fully rational agents are not required for money to emerge. In a similar perspective, other work considers the question of money emergence under heterogeneous beliefs, where some agents are rational, and the remaining fraction learns by an adaptive learning rule, showing that coordination is also eventually possible in this setting (Branch and McGough, 2016).
The Kiyotaki’s and Wright’s model (Kiyotaki and Wright, 1989, 1993) has been experimentally tested, to show if results obtained analytically or by numerical simulation were reproducible with actual human subjects. It had been shown that a monetary equilibrium can be reached with human subjects evolving in a search-theoretic environment (Brown, 1996; Duffy and Ochs, 1999; Duffy, 2001), or at least reaching a high proportion of speculators (Lefebvre et al., 2018). Interestingly, it has been shown that a reinforcement model fits well their experimental data obtained in a Kiyotaki-and-Wright’s environment (Kiyotaki and Wright, 1989, 1993), suggesting that although more sophisticated behavior rules were available, subjects tended to favor immediate past feedback (Duffy and Ochs, 1999; Duffy, 2001).
One first critic that we can address the computational and experimental aforementioned studies, is that although they succeeded in demonstrating achievements of monetary equilibrium, they were mainly considering the fundamental equilibrium of Kiyotaki and Wright (Kiyotaki and Wright, 1989, 1993). Indeed, Kiyotaki and Wright (Kiyotaki and Wright, 1989, 1993) consider two types of equilibrium: (i) fundamental, where the monetized good is less costly to store than the other goods in circulation, what explains easily why it is preferred, (ii) speculative, where some agents are required to incur at first supplementary costs (i.e., to speculate). The speculative equilibrium is particularly interesting, as it provides insight about a specific cognitive ability that could sustain money emergence (i.e., the ability to endorse a cost on short term with view on distant goals), and yet, it is the one for which the results are the scarcest (Brown, 1996; Duffy and Ochs, 1999; Duffy, 2001; Kindler et al., 2017; Lefebvre et al., 2018). Secondly, in contrast with virtual agents learning by reinforcement that are only provided with scarce information, human subjects had access to information about the global state of the economy in studies mixing the use of artificial agents and human subjects (Duffy and Ochs, 1999; Duffy, 2001; Lefebvre et al., 2018). Thirdly, to our knowledge, these computational and experimental studies are based on search-theoretic models involving only three goods (Brown, 1996; Duffy and Ochs, 1999; Duffy, 2001; Kindler et al., 2017; Lefebvre et al., 2018). In this case, only one type of agent uses the monetary good genuinely as a medium of exchange. It remains to know whether their conclusions can hold if there are more than three goods in circulation.
Let us note that in recent literature, numerous questions have been treated through an experimental money-emergence paradigm: Whether a convergence on a money equilibria is preferred to a gift exchange equilibria, where an agent has the possibility to give a good in the hope of obtaining another later (Duffy and Puzzello, 2014), how inflation tax affects economic activity (Anbarci et al., 2015), how a foreign money may be accepted by agents in an international framework (Jiang and Zhang, 2018; Ding et al., 2018), how a monetary equilibrium is reachable under assumption of a finite horizon (Davis et al., 2019), or even how when a first money already circulates in the economy, a second may emerge (Rietz, 2019). However, either they assume a central authority that injects money (Anbarci et al., 2015; Ding et al., 2018), either money does not emerge endogenously, as a fraction of agents is first provided with tokens (worthless goods that none agents consume) they are compelled to exchange to obtain their consumption good (Duffy and Puzzello, 2014; Jiang and Zhang, 2018; Davis et al., 2019; Rietz, 2019). In these experiments, the cognitive requirements for money emergence as an endogenous process are thus never explicitly tested.
The purpose of this study is to know whether economies populated with human subjects can reach a monetary state in the context of information scarcity, that is in a case of extremely incomplete information in the sense of the game theory, forcing the subjects to take their decisions under a strong form of ambiguity. More precisely, this study aims to investigate whether coordination over a unique medium of exchange can occur with subjects only experiencing the direct outcome of their decision, learning by trial-and-error and without any additional information.
Hence, the question is to know whether results obtained with virtual agents combining a restriction on computational abilities and informational input can be generalized to economies populated with humans. To assess their reliability and to broaden our conclusions, we decided to include an additional good, including in our study economies with four goods in circulation. To meet these goals, we borrowed certain elements from the previous search-theoretical models to define the structure of our economies, such as the production-consumption specialization and the absence of double coincidence of wants (i.e., if an agent produces \(i\) and consumes \(j\), no agent produces \(j\) and consumes \(i\), so that pure bartering is not an effective solution). However, instead of using an environment a la Kiyotaki and Wright (Kiyotaki and Wright, 1989, 1993), we decided to use a search-theoretical structure that presents more generality than Kiyotaki and Wright’s one, based on the Iwai’s model (Iwai, 1996). Iwai’s model differs in two fundamental ways from Kiyotaki and Wright’s model (Kiyotaki and Wright, 1989, 1993): (i) the exchange technology consists in random pairing inside markets specialized in a pair of good while in Kiyotaki and Wright (1989, 1993), agents are randomly matched regardless of any other characteristic (ii) there are no storage cost, such as storing a good \(i\) is not costlier than storing good \(j\). That is why we decided to adopt an Iwai-like environment with indistinguishable goods, in a way to avoid that money emergence bears on intrinsic features of goods, as it is in the case of the Kiyotaki and Wright’s fundamental equilibrium. We began by conducting a series of simulations. In the simulated economies, agents are producing a certain good and looking to obtain another one through exchanges, have little knowledge about the environment in which they operate—they only know if their attempt of exchange was a success or a failure. They are learning using a basic reinforcement mechanism, associating a value to each choice option available to them and updating by trial-and-error the efficiency of each type of exchange. We used the results of these simulations to identify the experimental conditions that would promote the coordination over a single medium of exchange. Subsequently, we observed the behaviors of human subjects under similar informational constraints and we compare the theoretical and experimental results. To conclude, we discuss the possibility of coordination over a unique medium exchange in the context of information scarcity, in a three and four goods setting.
Materials and methods
Model
General framework
Each economy is composed of different types of agents. A type of agent is defined by what agents of this type produce and consume. The goal of each agent is to obtain his consumption good. Agents proceed to exchanges between them to achieve this goal. Agents have feedback only about their exchange attempt and learn by reinforcement the efficiency of each type of exchange. We vary across simulations the distribution of agents among the existing types. By construction, if a good \(m\) becomes money, an agent that produces it or consumes it should try to exchange directly his production good against his consumption good. Otherwise, the agent is supposed to use it as a medium of exchange, that is to exchange his production good against \(m\), and then \(m\) against his consumption good.
Production-consumption specialization
We consider an economy with \(G\) goods in circulation, with \(G\ \ge \ 3\). We denote these goods \(1,2,\ldots,G\). Each agent is specialized in production and consumption. A agent of type \((i,j)\) produces good \(i\) and consumes good \(j\) (with \(j\,\ne\, i\)). We suppose a non double coincidence of needs: if an agent of type \((i,j)\) exists, then an agent of type \((j,i)\) does not exist. We use a minimally connected endowment-need distribution (Iwai, 1996), such that existing agent types are: \((G,1),(1,2),\ldots ,(G-1,G)\). The number of agents for each type is exogenously set. We designate by \({x}_{G1}\) the number of agent of type \((G,1)\), \({x}_{12}\) the number of agent of type \((1,2)\), ..., \({x}_{G-1G}\) the number of agent of type \((G-1,G)\). Each agent enters the economy equipped with a unit of its production good. Each time an agent receives its consumption good, it consumes it and immediately after, produces a new unit of its production good (each agent owns a single storage unit).
Exchange technology
The exchange technology relies on a trading-post mechanism (Iwai, 1996). At each time step, each agent chooses the type of exchange it wants to perform, depending on the good it has in hand. This choice determines to which market it goes. There is an equal number of markets and goods in circulation. Each market is specialized in a pair of good \((i,j)\), such as in the \(ij\)-market it is possible to exchange \(i\) against \(j\), and \(j\) against \(i\). Our trading technology works synchronously (i.e., all exchanges occur simultaneously). Thus, in each \(ij\)-market, we randomly associates each i-seller – j-buyer to a j-seller – i-buyer, if there is a sufficient number of j-sellers– i-buyers. Therefore, in each \(ij\)-market, the probability of successfully exchanging a good \(i\) against a good \(j\) depends on the respective number of i-sellers – j-buyers and j-sellers– i-buyers (e.g., if there is in the \(ij\)-market at time \(t\), 4 \(i\)-sellers – \(j\)-buyers and 8 \(j\)-sellers – \(i\) buyers, 4 \(ij\)-exchanges will take place and the probability of success for a \(i\)-seller – \(j\) buyers is 0.5 while a \(j\)-seller – \(i\)-buyer will proceed to the desired exchange with certainty).
Information scarcity
An agent does not know other agents’ choices, nor the probabilities of success of each exchange: the only information it has access to is whether or not it succeeded in the desired exchange.
Strategies
The goal of each agent is to obtain as quickly as possible his consumption good.
We will specifically consider:
The direct exchange strategy. For a type-\(ij\) agent with \(i\) in hand (his production good), it consists of trying an exchange against \(j\) (his consumption good).
The indirect exchange strategy with \(k\) as a medium of exchange. For a type-\(ij\) agent with \(i\) in hand (his production good), it consists of trying an exchange against the good \(k\) (with \(k\,\ne\, i,j\)). With \(k\) in hand, it consists of trying an exchange against \(j\) (his consumption good).
Simulations
Decision-making process
Each agent learns to estimate the success rate of each type of exchange. This allows it to estimate the time needed to get its consumption good depending on the choice is made.
Success rate estimates for each exchange type are based on a reinforcement learning process. At time step \(t\), when an agent attempts to exchange \(i\) against \(j\), it updates the success rate estimation associated to the exchange of type \((i,j)\), noted \({e}_{ij}\) according to:
with \(\alpha \in [0,1]\), a free parameter and \(s\), a binary variable such as \(s=1\) if the agent succeeded in his exchange, \(0\) otherwise. \(\alpha\) is a learning rate which defines to which extent an agent takes into account his latest attempted exchange. If \(\alpha =1\), the agent considers only his latest attempted exchange. If \(\alpha =0\), the agent does not take into account the new observations of failure or success of the last attempted exchange.
When making a decision, each agent considers the expected temporal interval between the time of choice and the time he gets his consumption good. It is assumed that the longer the time interval, the lower the value for the agent. Let \(v(ij)\) be the value associated to the choice \(ij\) (i.e., exchange \(i\) against \(j\)) and \({\Delta }_{ij}\) the estimation by the agent of the time that will be spent before consumption if he chooses \(ij\):
with \(\beta \ >\ 0\), a free parameter. \(\beta\) is a discount factor parameter: the closer to \(0\), the more subjective values are discounted with time (Osborne, 2016). Since it takes at least one unit of time for the agent to get its consumption good, the value function \(v\) is bounded between 0 and 1.
We assume that for each exchange of type \((i,j)\), the agent has an estimation of the success rate associated to this type of exchange (\({e}_{ij}\)). The higher the estimated success rate, the lower the estimated time to succeed in this exchange. Let \({\delta }_{ij}\) be the estimated time to achieve a type-\(ij\) exchange:
For a type-\(ij\) agent, \({\Delta }_{ij}={\delta }_{ij}\). If a type-\(ik\) agent (with \(k\,\ne\, j\)), the value of \({\Delta }_{ij}\) depends on the action policy chosen by the agent, as \({\Delta }_{ij}\) would be equal in this case to the sum of the \(\delta\)-values for each intermediary exchange planned by the agent. For instance, for a type-\(ik\) agent following an indirect exchange strategy with good \(j\), \({\Delta }_{ij}={\delta }_{ij}+{\delta }_{jk}\). An exhaustive description of valuation functions for the specific case where \(G=3\) is given in the supplementary section.
Agents make decisions using a probabilistic decision rule. The standard approach is to use a softmax function to introduce stochasticity in choice (Sutton and Barto, 1998). However, Apesteguia and Ballester (2018) show that the combination of a softmax rule and either a risk-sensitivity or a temporal discounting model can be problematic, as the parameter describing the risk-sensitivity discounting effect can have a non-monotonic effect on the variable of interest. For this reason, the rule implemented is a simple \(\epsilon\)-rule (Sutton and Barto, 1998). Let \(v(ij)\) be the value associated with choice \(ij\) and \(p(ij)\), the probability to choose to exchange \(i\) against \(j\). \(p(ij)\) is computed as follows:
with \(\gamma \in [0,1]\), a free parameter. \(\gamma\) is an exploitation-exploration rate (Sutton and Barto, 1998): the lower the \(\gamma\)-value, the more prone the agent will be to choose the option with the highest subjective value. On the contrary, the higher the \(\gamma\)-value, the more the agent will be prone to choose another option.
Protocol and parametrization
We ran \(10,800\) simulations with \(G=3\) and \(10,800\) simulations with \(G=4\). Each simulation lasted \(100\) time-steps. The exploration parameter (\(\epsilon\)) was varied between \(0.10\) and \(0.15\). The learning rate (\(\alpha\)) was varied between \(0.10\) and \(0.25\). The discount factor (\(\beta\)) was varied between \(0.80\) and \(1.20\). The initial values of success rate estimates for all types of exchange were set to \(1\). The fact that the initial values were set to \(1\) precluded the presence of bias in preferences (such as bias such as the appearance of commodity money was more likely). With these values, the value associated with exchanging his production good against his consumption good was indeed higher than the value of any other exchange for all agents, implying that all agents were preferring the direct exchange strategy at the first time-step.
When \(G=3\), \({x}_{31}\) was set to \(50\) while \({x}_{12}\) and \({x}_{23}\) were varied between \(10\) and \(200\).
When \(G=4\), \({x}_{41}\) and \({x}_{12}\) were set to \(50\) (following results from simulations with \(G=3\)) while \({x}_{23}\) and \({x}_{34}\) were varied between \(10\) and \(200\).
Artificial experiments
We ran \(4\) separate simulations before the experiment using the same distribution of agents as for experiments (\(2\) matching the conditions of Experiment I and \(2\) matching the conditions of Experiment II). The cognitive parametrization of the agents was: \(\alpha =0.175\), \(\beta =1.000\) & \(\gamma =0.125\) (these values correspond to the average value of each parameter used for the simulations).
Post-hoc simulations
We fitted our behavioral data on the decision-making model using Scipy’s (Jones et al., 2001) differential evolution algorithm (provided by the module optimize). We optimized model parameters by minimizing the negative log-likelihood of the model for each subject individually.
Using the best-fit parameter values of the subjects to parametrize the artificial agents (the distribution of the best-fit parameter values is given in Fig. S18A of the Supplementary Section), we ran \(4\) post-hoc simulations (\(2\) matching the conditions of Experiment I and \(2\) matching the conditions of Experiment II).
Experiment I
Subjects
Sixty-six subjects have been recruited by the Maison des Sciences Économiques (106–112, boulevard de l’Hôpital, 75013 Paris, France). The ethics approval for this project was provided by the Institutional Review Board of the Paris School of Economics. In line with ethical guidelines, all participants provided their informed consent before proceeding to the experiment and filled in a survey asking their age and gender. Financial compensation of \(10\) euros was offered to each participant, with a bonus proportional to their score (a subject earned a point when he succeeded to obtain its consumption good and each point corresponded to \(0.20\) euros). The average reward was \(15.41\) euros (\(\pm\! 1.80\) STD). We noticed a gender parity (women represented \(48.5\)% and men \(51.5\)%). The average age was \(29.42\) (\(\pm\! 12.55\) STD).
Task
A subject plays the role of a producer of a good \(i\) and a consumer of a good \(j\), in an economy comprising either \(30\) (uniform condition) or \(36\) (non-uniform condition) subjects. During \(50\) time steps, he has to choose which type of exchange he wants to try, among two options (e.g., with good \(1\) in hand, he has to choose between trying to exchange good \(1\) against good \(2\), or good \(1\) against good \(3\)). The only information he gets is whether he succeeded or not in the exchange. Further details are provided in the supplementary section.
User interface
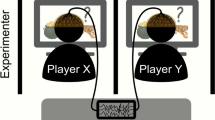
Following the assumption that a visually appealing serious-game would increase the subject’s engagement (Wanner, 2014; Comello et al., 2016) and induce naturalistic decision-making (Harrison and List, 2004), we chose to design a game-inspired interface instead of a textual interface (see Fig. 1).
Experimental conditions
All goods being identical, we arbitrarily chose the good \(1\) as the ‘target’, that is to say, the good that we wanted to see emerge. Following the simulation results, we contrasted two modes of distributions, either promoting the money emergence or precluding it. Each subject went through only one of the two conditions. The conditions differ by the distribution of agents among types.
Uniform (U). There is an equal number of agents of each type.
Non-uniform and promoting the use of a medium of exchange (NUPM). The number of agents for a specific type depends on whether this type involves producing or consuming a specific good, that we arbitrarily chose to be the good \(1\). The number of agents for a type meeting this condition is half the number of agents of a type not meeting this condition.
The two conditions were the following:
- 1.
\(G=3\) and U-distribution. \({x}_{31}\), \({x}_{12}\) and \({x}_{23}\) were set to 10.
- 2.
\(G=3\) and NUPM-distribution. \({x}_{31}\) and \({x}_{12}\) were equal to 9 but the value of \({x}_{23}\) was doubled (18)—the choice of setting \({x}_{31}\) and \({x}_{12}\) to 9 instead of 10 and \({x}_{23}\) to 18 instead of 20 is due to the absence of some subjects the day the experiment took place.
Analysis
With three goods in circulation, one type of agent can use the good \(1\) as a medium of exchange: Agents that produce good \(2\) and consume good \(3\). We thus measured for each agent belonging to the type (\(2\), \(3\)), the indirect exchange rate involving good \(1\). That is the frequency rate at which a subject of type (\(2\), \(3\)) asks for the good \(1\) to use it as a medium of exchange to get his consumption good \(3\) from his production good \(2\). For statistical analysis of the human experiment as well the experiment-like simulations, we averaged this measure overtime for the last third of the trials, to assert learning curves were stable. We then compared these results across uniform and non-uniform distributions of agent types. As we did not expect a normal distribution of data due to clustering effects at the boundaries of our scale, assessment of statistic relevance of our observations has been made with Mann–Whitney’s U ranking test (Mann and Whitney, 1947), applying Bonferroni’s corrections for multiple comparisons. We set the significance threshold at 5%.
Experiment II
Subjects
100 subjects have been recruited under the same conditions as for Experiment I. The remuneration was computed the same way and the average reward was \(14.29\) euros (±1:53 STD). We also noticed a gender parity (women represented \(50.0 \%\) and men \(50.0 \%\)). The average age was \(28.97\) years old (±13:01 STD).
Task
The task is similar to Experiment I, except that they were 4 goods in circulation and that economies were comprising either \(40\) (uniform condition) or \(60\) (non-uniform condition) subjects. Also, as a consequence of having 4 goods in circulation, subjects were having 3 alternatives each time, instead of 2 (for instance, with the good \(1\) in hand, they had a choice between trying to exchange it against the good \(2\), \(3\) or \(4\)).
Experimental conditions
As in experiment I, the parametrization of the economies for each condition has been based on the simulation results (see Fig. 2). Hence, the distribution was either uniform (U), either non-uniform promoting the use of a medium of exchange (NUPM):
- 1.
\(G=4\) and U-distribution. \({x}_{41}\), \({x}_{12}\), \({x}_{23}\), \({x}_{34}\) were set to 10.
- 2.
\(G=4\) and NUPM-distribution. \({x}_{41}\), and \({x}_{12}\) were still equal to 10 but the values of \({x}_{23}\) and \({x}_{34}\) were doubled (\(20\)).
Simulation: Influence of agents distribution on the use of a medium of exchange. Based on these simulation results, we deduced the optimal experimental conditions required to see money emerge with human subjects. a The phase diagram summarizes the results of 10,400 simulations with 3 goods.The number of type (\(3\), \(1\)) agents is set to 50 while the number of agents of type (\(1\), \(2\)) and (\(2\), \(3\)) varies between 10 and 200 (corresponding, respectively, to the values on the \(x\)-axis and \(y\)-axis). The hotter the color, the higher the indirect exchange frequency involving good \(1\) as a medium of exchange. In a three goods economy, the highest frequency of indirect exchanges with good \(1\) observed is when the value \({x}_{12}\) as well the value of \({x}_{23}\) is nearly twice that of \({x}_{31}\). b Similarly, the phase diagram on B panel summarizes the results of 10,400 simulations with 4 goods. The number of agent of types (\(4\), \(1\)) and (\(1\), \(2\)) is set at 50 while the the number of agents of type (\(2\), \(3\)) and (\(3\), \(4\)) varies between 10 and 200 (corresponding, respectively, to the values on the \(x\)-axis and \(y\)-axis). In a four goods economy, the highest frequency of indirect exchanges with good \(1\) observed is when the value \({x}_{23}\) as well the value of \({x}_{34}\) is nearly twice that of \({x}_{12}\) and \({x}_{41}\).
Analysis
With four goods in circulation, two agent types can use the good \(1\) as a medium of exchange: Agents that produce good \(2\) and consume good \(3\) and agents that produce good \(3\) and consume good \(4\). We measured for each agent belonging to the type \((2,3)\) and \((3,4)\) the frequency rate at which a subject asks to trade its production good for the good \(1\) to obtain its consumption good. For statistical analysis of the human experiment as well the experiment-like simulations, we averaged this measure overtime for the last third of the trials, to assert learning curves were stable. We then compared these results across the uniform and non-uniform distribution of agent types. As we did not expect a normal distribution of data due to clustering effects at the boundaries of our scale, assessment of statistic relevance of our observations has been made with Mann-Whitney’s U ranking test (Mann and Whitney, 1947), applying Bonferroni’s corrections for multiple comparisons. We set the significance threshold at \(5 \%\).
The Supplementary section provides further details, and in particular a summary of the experiment parametrization in Tables S1 and S2.
Results
Simulations
3 goods setting
When \(G=3\), the highest frequency of indirect exchanges with good \(1\) is observed when the value of \({x}_{31}\) is equal to that of \({x}_{12}\) and when the value of \({x}_{23}\) is at least twice that of \({x}_{31}\) (see Fig. 2). One may notice that the use of a uniform distribution of agent types (\({x}_{31}=50\), \({x}_{12}=50\), \({x}_{23}=50\)) results in a low frequency of indirect exchanges with good \(1\).
4 goods setting
When \(G=4\), the highest frequency of indirect exchanges with good \(1\) is observed when the values of \({x}_{23}\) and \({x}_{34}\) are nearly twice that of \({x}_{41}\) and \({x}_{12}\) (see Fig. 2). The use of a uniform agent type distribution (\({x}_{41}=50\), \({x}_{12}=50\), \({x}_{23}=50\), \({x}_{34}=50\)) results in a low frequency of indirect exchanges with good \(1\).
Experimental setup
Put together, these results led us to formulate the following operational hypotheses regarding our experiments: (i) setting the number of one particular type of agents to half of the other agent types promotes the use of its production good as a medium of exchange (ii) setting the number of agents of each type equal precludes the emergence of a medium of exchange.
Hence, for the Experiment I, we set the value of \({x}_{12}\) equal to that of \({x}_{31}\) and set the value of \({x}_{23}\) twice that of \({x}_{31}\) for the simulations under experimental conditions with \(G=3\) where our goal was to promote money emergence (see Fig. 3). For the Experiment II, we set the value of \({x}_{12}\) equal to that of \({x}_{41}\) and to set the value of \({x}_{23}\) and \({x}_{34}\) twice that of \({x}_{41}\) for the simulations under experimental conditions with \(G=4\) where our goal was to promote money emergence (see Fig. 4).
Experiment I: The use of a medium of exchange with three goods in circulation. We contrast the U-distribution of agent types (blue color) with the NUPM-distribution (orange color). In a three goods economy, only the (\(2\), \(3\)) type of agent can use Good \(1\) as money. The left side plots represent the moving median (±STD) of the frequency of use of a medium of exchange for each individual over time with a 25 time-step window. On the box plots (right side), each dot represents the averaged frequency over time for either one artificial agent (panel a and panel c), or one human subject (panel b) belonging to the (\(2\), \(3\)) agent type. The gray dotted lines indicate the chance level. a We observe that in the NUPM-distribution, the median frequency of indirect exchanges involving good \(1\) is significantly greater than in the U-distribution (\(p\ <\ 0.05\)), showing that the good \(1\) is used as a medium of exchange significantly more frequently in the NUPM-distribution than in the U-distribution. b We replicate this result with human subjects: in the NUPM-distribution, the median frequency of indirect exchanges involving good \(1\) is significantly greater than in the U-distribution (\(p\ <\ 0.05\)). c Running post-hoc simulations with the best-fit parameters of the human subjects, we obtain the same pattern as the experimental results: the median frequency of indirect exchanges involving good \(1\) is significantly greater than in the U-distribution (\(p\ <\ 0.05\)).
Experiment II: The use of a medium of exchange with three goods in circulation. We contrast the U-distribution of agent types (blue color) with the NUPM-distribution (orange color). In a four goods economy, two types of agents that can use good \(1\) as money: (\(2\), \(3\)) and (\(3\), \(4\)). The left side of each pair of plots represents the moving median (±STD) of the frequency of use of a medium of exchange for each individual over time with a 25 time-step window. On the box plots (right side), each dot represents the averaged frequency over time for either one artificial agent (panel a and panel c), or one human subject (panel b). Results for (\(2\), \(3\)) agents are depicted on the two leftmost figures of each panel, while results for (\(3\), \(4\)) are depicted on the two rightmost plots. The gray dotted lines indicate the chance level. a In simulations and with regards to (\(2\), \(3\)) agents, we observe that in the NUPM-distribution, the median frequency of indirect exchanges involving good \(1\) is significantly greater than in the U-distribution (\(p\ <\ 0.05\)), showing that good \(1\) is used a medium of exchange significantly more in the NUPM-distribution than in the U-distribution. Similarly, with artificial agents that belong to the (\(3\), \(4\)) type, we observe that in the NUPM-distribution, the median frequency of indirect exchanges involving good \(1\) is significantly greater than in the U-distribution (\(p\ <\ 0.05\)). b We do not replicate the simulation results from panel a with human subjects: the frequency of indirect exchanges with good is not significantly different from the U-distribution (\(p\ >\ 0.05\)). Similarly, we do not replicate the simulation results from panel b with human subjects (\(p\ >\ 0.05\)). c Running post-hoc simulations with the best-fit parameters of the human subjects, we obtain the same pattern as the experimental results: the median frequency of indirect exchanges involving good \(1\) are not significantly greater than in the U-distribution for both agent types that are concerned (\(p\ >\ 0.05\)).
Experiment I
Artificial experiment
To make predictions about the experiment with human subjects, we ran \(2\) additional simulations, using a parametrization identical to the two experimental conditions (see Table S1). In one of the two conditions, we used a uniform distribution types while in the other, we promoted the use of good \(1\) as a medium of exchange, by using a non-uniform distribution of agent types (one can note that as all the goods are identical, the choice to promote good \(1\) is arbitrary).
With \(G=3\) (see Fig. 3), we observe that the median frequency of indirect exchanges with good \(1\) by agents of type \((2,3)\) is (i) above chance level, and (ii) significantly greater in the NUPM–distribution than in the U-distribution (\(U=21.0\), \(p\ <\ 0.00{1}^{* }\), \(n=28\)). This means that agents that neither produce the good \(1\) nor consume it try to obtain it when they have their production good in the hand and, once in the hand, try to obtain their consumption good using it as an intermediary good.
Human experiment
In line with the results of the simulation, we observe that the median frequency of indirect exchanges with good \(1\) by subjects of type \((2,3)\) is (i) above chance level, and (ii) significantly greater in the NUPM–distribution than in the U-distribution (\(U=50.5\), \(p=0.03{1}^{* }\), \(n=28\)).
Post-hoc simulations
The simulations using the best-fit parameter values led to results that have the same pattern as the experimental results. With three goods we observe that the median frequency of indirect exchanges with good \(1\) by agents of type (\(2\), \(3\)) is significantly greater in the NUPM-distribution than in the U-distribution (\(U=48.0\), \(p=0.02{3}^{* }\), \(n=28\)).
Experiment II
Artificial experiment
To make predictions about the experiment with human subjects, we ran two additional simulations, using a parametrization identical to the two experimental conditions (see Table S2). In one of the two conditions, we used a uniform distribution types while in the other, we promoted the use of good \(1\) as a medium of exchange, by using a non-uniform distribution of agent types (one can note that as all the goods are identical, the choice to promote good \(1\) is arbitrary).
With \(G=4\), two types of agent are able to use good \(1\) as a medium of exchange: \((2,3)\) and \((3,4)\). We observe that the median frequency of indirect exchanges with good \(1\) by \((2,3)\) agents (see Fig. 4a) is (i) above chance level, and (ii) significantly greater in the NUPM–distribution than in the U-distribution (\(U=21.0\), \(p\ <\ 0.00{1}^{* }\), \(n=30\)). Similarly, the median frequency of indirect exchanges with good \(1\) by \((3,4)\) agents (see Fig. 4b) (i) is above chance level, and (ii) significantly greater in the NUPM–distribution than in the U-distribution (\(U=28.0\), \(p=0.00{2}^{* }\), \(n=30\)).
Human experiment
For the condition with \(G=4\), we expected the use of the good \(1\) as money to be promoted by both agent types \((2,3)\) and \((3,4)\). But contrary to what has been observed in the artificial agents, the median frequency of indirect exchanges with good \(1\) by agents of type \((2,3)\) (see Fig. 4a) is not significantly greater in the NUPM–distribution than in the U-distribution (\(U=56.0\), \(p=0.056\), \(n=30\)). Similarly, the median frequency of indirect exchanges with good \(1\) by agents of type \((3,4)\) (see Fig. 4b) is not significantly greater in the NUPM–distribution than in the U-distribution (\(U=77.5\), \(p=0.333\), \(n=30\)).
Post-hoc simulations
The simulations using the best-fit parameters value led to results that have the same pattern as the experimental results. The median frequency of indirect exchanges with good \(1\) by agents of type \((2,3)\) is not significantly different in the NUPM-distribution than in the U-distribution (\(U=99.0\), \(p=0.982\), \(n=30\)), as well as for agents of type \((3,4)\) (\(U=78.5\), \(p=0.355\), \(n=30\)).
Supplementary section provides more details for both experiments, in particular a summary of the statistical tests (see Table S3), a short demographic analysis (see Figs S1, S2, and Table S4), the representation of individual behavior (see Figs S3 and S4), a sensitivity analysis to free parameters (see Fig. S5 and Table S5), some post hoc simulations varying some environment parameters and also using alternative decision-making models (see Figs S7, S8, S10–S17, and Tables S7 and S8), more details about the model fitting and a model comparison (see Figs S6, S18, S19, and Tables S6, S9, S10).
Discussion
The results obtained by simulation are in line with our initial assumption: the emergence of commodity money is possible in a decentralized economy with agents endowed with limited computational abilities and having very poor information on the global state of the economy. Indeed, they show that manipulating the agent type distribution is sufficient to foster the emergence of a unique medium of exchange in a 3 goods economy, as well as in a 4 goods economy.
To assess the robustness of these computational results, we conducted two experiments. In contrast to previous experimental studies (Marimon et al., 1990; Duffy, 2001; Kindler et al., 2017), human subjects did not have access to any statistic regarding the current state of the economy in which they were evolving, and in particular the choices of the other participants. The only feedback that they got at each iteration of the game was whether the exchange was successful. Also, contrary to recent experimental studies (Duffy and Puzzello, 2014; Anbarci et al., 2015; Ding et al., 2018; Jiang and Zhang, 2018; Davis et al., 2019; Rietz, 2019), there is no monetary authority, and money emerges endogenously since no good is intrinsically devised to become a medium of exchange.
In the 3 goods setting experiment, the experimental results were consistent with the computational results, the manipulation of the agent type distribution being effective in promoting the use of a unique medium of exchange. Although, in the 4 goods setting experiment, this manipulation turned out to be ineffective. The results with a 3 goods economy extend precedent works in artificial agents and human using the Kiyotaki and Wright’s framework (Marimon et al., 1990; Duffy, 2001; Kindler et al., 2017). In particular, it shows that coordination over a unique medium of exchange is also possible in an Iwai-like environment (Iwai, 1996). Furthermore, it shows that the monetary coordination does not even require agents to have extended knowledge of other players’ preferences or to construct a sophisticated belief system: a trial and error approach—in our case, a simple reinforcement learning mechanism—is sufficient. Of course, this coordination between agents over a unique medium of exchange is not systematic: our results suggest that structural constraints are necessary, such as a non-equal distribution of agents over types in our environment. This can be interpreted as the fact that a particular endowment-need distribution can render sensitive the benefits of coordinating on a unique medium of exchange, thus highlighting interaction effects between economic structure and agents’ cognition.
However, by raising the number of goods from 3 to 4, and placing human subjects under the same conditions as our artificial agents, we were not able to replicate the results obtained by simulations. This failure may carry several interpretations. We tackle some of those thereafter. Except for the first one, they have in common to assume that an additional good greatly increases the difficulty to coordinate, which is the most probable cause of failure. (i) “It is due to specific features of the sample”. We possess data from one hundred subjects, but this corresponds to data for only two economies and we expected convergence for only one of them. It is indeed difficult to reject the possibility that the lack of convergence over a medium of exchange for the concerned economy is specific to our sample.
(ii) “The subjects (or a sub-group of the subjects) were unable to endorse the primary cost of indirect exchange (i.e., they have a strong bias towards a direct exchange strategy)”. Indeed, in a Kiyotaki & Wright environment (Kiyotaki and Wright, 1989, 1993), in the specific case where a speculative equilibrium is expected—that is to say when the monetary good has a higher storage cost than the other good—it has been noted that a non-negligible part of subjects had difficulties to endorse the primary cost implied by the use of the monetary good as a medium of exchange (i.e., to speculate) (Duffy and Ochs, 1999; Kindler et al., 2017). It means that some subjects that neither produce or consume the monetary good were reluctant to engage in indirect exchange strategies. Similarly, our experimental results show that part of the subjects that were supposed to proceed to indirect exchanges and suffer from a primary temporal cost, did not adopt such strategies, although most of the subjects that were supposed to use direct exchanges did so (see for instance the results for the condition with a non-uniform distribution promoting the good \(1\) with four goods depicted in the Fig. 4). As in our protocol, subjects do not play against artificial agents that use a deterministic algorithm but against other human subjects, it is nonetheless difficult to tell whether subjects playing (almost) always a direct exchange strategy did it because of the behavior of other subjects, or because they were initially strongly biased toward this option.
(iii) “Subjects were lacking information to coordinate”. Since the level of information for artificial agents was strictly identical to that of humans, it is probably for other reasons than because of a lack of information. Indeed, reinforcement learning, although effective, is far from being the most sophisticated learning model. It is unlikely that human subjects have failed to coordinate on a single medium of exchange due to more limited cognitive abilities than agents using reinforcement learning.
(iv) “The psychological model used for the simulations is unappropriated, that is the reason why it was partly ineffective in producing accurate predictions”. Several studies point out the fact that reinforcement learning models fit well the behavior of human subjects in economic contexts (Roth and Erev, 1995; Erev and Roth, 1998; Feltovich, 2000), and specifically for modeling behavior in a coordination game over a unique medium of exchange (Duffy and Ochs, 1999; Duffy, 2001; Kindler et al., 2017). However, to test the relevance of such an interpretation, we proceeded to a post hoc analysis (see Supplementary section).
We fitted the behavioral data with our reinforcement learning model, and run simulations using the best-value parameters of each subject. We obtained the same pattern as the experimental results: in the three-goods setting, the use of a medium of exchange is promoted in the condition of non-uniform distribution while in the four-goods setting, the use of a medium of exchange was not promoted as we expected. Hence, using the adequate set of cognitive parameters, we could replicate the experimental results, whether positive or null.
(v) “Assuming the cognitive model as true, this could be because the artificial agents from a single economy were having homogeneous cognitive features, while it exists certain heterogeneity among the human subjects that could make the coordination more difficult”. To test the relevance of this interpretation, after fitting the behavioral data with the model, we simulated an homogeneous population using as cognitive parameter values the average best value for each cognitive parameter after fitting the behavioral data (instead of simulating an heterogeneous population with the parameters of a single agent being the best-value parameters of a subject fit). However, the pattern remained unchanged: the non-uniform distribution of agent types promotes the use of a medium of exchange with three goods, but not with four.
(vi) “More trials would have allowed subjects to overcome the complexity of coordination at 4 goods”. To test the relevance of this interpretation, after fitting the behavioral data with the model, we simulated a population of (heterogeneous) agents with the parameters of every single agent being the best-fit parameter values of a single subject for a larger number of iteration (\(n=500\) instead of \(50\)). Here, the results changed (see Supplementary section), as the non-uniform distribution of agent types promotes the use of a medium of exchange in both settings with a large number of trials. This indicates that an extended time could have allowed the human subjects to modify slowly their behavior towards the use of a medium of exchange, raising the questions about the pragmatic possibility of such large scale experiments for a long time.
Nevertheless, these results seem to contribute to a better understanding of the processes underlying the coordination over a unique medium of exchange. Hence, in the 3 goods setting, the results in artificial agents, as well as those obtained in human, show that decision-makers do not need to have any expertize concerning the economic system in which they evolve to allow this system to acquire certain remarkable macroeconomic properties—such as the existence of a unique medium of exchange. Said differently, these results show that the members of an economic system do not need to know the macroeconomic properties of the system to be able to influence them.
Although, the attempt to test the robustness of the results by considering a 4 good setting appears to be unsuccessful. The results obtained by simulation and with human subjects being not completely in line, it is difficult to draw strong inferences regarding the possibility of money emergence under informational constraints in a more than three goods economy. Also, these negative results indicate the importance to take into account the temporal aspect of the coordination processes: even if we possess evidence for the existence of a steady-state for an economic system with artificial agents (or by mathematical proof), it could be that, due to the complexity of the coordination process, the time for obtaining with humans is so long that in real-world context, it would be a good approximation to say that it would never occur. At least, in the present context of money, the phenomenon already occurred, so it just remains to continue to investigate how such large scale coordination has been possible, given the complexity of the interactions.
In previous studies (Duffy and Ochs, 1999; Duffy, 2001; Lefebvre et al., 2018), subjects were constantly provided with economy statistics, such as the current distribution of goods or agent types. From this information, subjects can infer exchanges’ success probabilities. In that sense, decisions are made by description: subjects learn about the probabilistic consequences of their action by consulting descriptions of action consequences and probabilities. In contrast here, subjects are not provided with any information related to the state of the economy, decisions are therefore made by experience: subjects’ learning of outcome probabilities is based on their own experience. In the literature, one concept refers to these two kinds of decision-making systems supposed to result in behavioral discrepancies: the description-experience gap (Wulff et al., 2018).
It has been observed that decision by experience is subject to biases that are absent in decision by description. Preferential learning from positive outcomes (rather than negative outcomes) prediction errors is for instance often observed (Palminteri et al., 2017; Lefebvre et al., 2017; den Ouden et al., 2013; Frank et al., 2007; Van Den Bos et al., 2012; Aberg et al., 2016). Interestingly, our subjects also present this asymmetry in value-update and seem to preferentially learn from exchanges that result in better-than-expected outcomes (see Fig. S18F). Investigating how such bias affects the coordination of agents in an experience-based money emergence paradigm could then constitute a relevant subject for further studies.
Data availability
The data are available at the same address than the analysis program: https://github.com/AurelienNioche/MoneyAnalysis.
Code availability
The software we used was based on a client/server architecture. The client part has been developed using the Unity game engine. The application ran on 7″ Android tablets. The assets of the application are available at https://github.com/AurelienNioche/MoneyApp. The experiment server was hosted on a local server and has been developed in Python. The code of the server part is available at https://github.com/AurelienNioche/MoneyServer. The analysis program is available at https://github.com/AurelienNioche/MoneyAnalysis.
References
Aberg KC, Doell KC, Schwartz S (2016) Linking individual learning styles to approach-avoidance motivational traits and computational aspects of reinforcement learning. PLoS ONE 11(11):e0166675
Aiyagari SR, Wallace N (1991) Existence of steady states with positive consumption in the kiyotaki-wright model. Rev Econ Stud 58(5):901–916
Anbarci N, Dutu R, Feltovich N (2015) Inflation tax in the lab: a theoretical and experimental study of competitive search equilibrium with inflation. J Econ Dynam Control 61:17–33
Apesteguia J, Ballester MA (2018) Monotone stochastic choice models: the case of risk and time preferences. J Polit Econ 126(1):74–106
Branch W, McGough B (2016) Heterogeneous beliefs and trading inefficiencies. J Econ Theory 163:786–818
Brown PM (1996) Experimental evidence on money as a medium of exchange. J Econ Dynam Control 20(4):583–600
Comello MLG, Qian X, Deal AM, Ribisl KM, Linnan LA, Tate DF (2016) Impact of game-inspired infographics on user engagement and information processing in an ehealth program. J Med Internet Res 18:9
Davis DD, Korenok O, Norman P, Sultanum B, Wright R (2019) Playing with Money. FRB RichmondWorking Paper No. 19–2. Available at SSRN: https://ssrn.com/abstract=3333603
den Ouden HE, Daw ND, Fernandez G, Elshout JA, Rijpkema M, Hoogman M, Franke B, Cools R (2013) Dissociable effects of dopamine and serotonin on reversal learning. Neuron 80(4):1090–1100
Diamond P (1984) Money in search equilibrium. Econom J Econom Soc 1–20
Ding S, Lugovskyy V, Puzzello D, Tucker S, Williams A (2018) Cash versus extra-credit incentives in experimental asset markets. J Econ Behav Organization 150:19–27
Duffy J (2001) Learning to speculate: experiments with artificial and real agents. J Econ Dynam Control 25(3–4):295–319
Duffy J, Ochs J (1999) Emergence of money as a medium of exchange: an experimental study. Am Econ Rev 89(4):847–877
Duffy J, Puzzello D (2014) Gift exchange versus monetary exchange: theory and evidence. Am Econ Rev 104(6):1735–1776
Erev I, Roth AE (1998) Predicting how people play games: reinforcement learning in experimental games with unique, mixed strategy equilibria. Am Econ Rev 88(4):848–881
Feltovich N (2000) Reinforcement-based vs. belief-based learning models in experimental asymmetric-information games. Econometrica 68(3):605–641
Frank MJ, Moustafa AA, Haughey HM, Curran T, Hutchison KE (2007) Genetic triple dissociation reveals multiple roles for dopamine in reinforcement learning. Proc Natl Acad Sci 104(41):16311–16316
Harrison GW, List JA (2004) Field experiments. J Econ Literature 42(4):1009–1055
Iwai K (1996) The boostrap theory of money: a search-theoretic foundation of monetary economics. Struct Change Econ Dynamics 7(4):451–477
Jiang JH, Zhang C (2018) Competing currencies in the laboratory. J Econ Behav Organization 154:253–280
Jones E, Oliphant T, Peterson P (2001) SciPy: open source scientific tools for Python
Jones RA (1976) The origin and development of media of exchange. J Polit Eco 84(4, Part 1):757–775
Kehoe TJ, Kiyotaki N, Wright R (1993) More on money as a medium of exchange. Econ Theory 3(2):297–314
Kindler A, Bourgeois-Gironde S, Lefebvre G, Solomon S (2017) New leads in speculative behavior. Phys A Stat Mech Appl 467:365–379
Kiyotaki N, Wright R (1989) On money as a medium of exchange. J Polit Econ 97(4):927–954
Kiyotaki N, Wright R (1991) A contribution to the pure theory of money. J Econ Theory 53(2):215–235
Kiyotaki N, Wright R (1993) A search-theoretic approach to monetary economics. Am Econ Rev 83(1):63–77
Lefebvre G, Lebreton M, Meyniel F, Bourgeois-Gironde S, Palminteri S (2017) Behavioural and neural characterization of optimistic reinforcement learning. Nat Hum Behav 1(4):0067
Lefebvre G, Nioche A, Bourgeois-Gironde S, Palminteri S (2018) Contrasting temporal difference and opportunity cost reinforcement learning in an empirical money-emergence paradigm. Proc Natl Acad Sci 115(49):E11446–E11454
Luo GY (1998) The evolution of money as a medium of exchange. J Econ Dynam Control 23(3):415–458
Mann HB, Whitney DR (1947) On a test of whether one of two random variables is stochastically larger than the other. Ann Math Stat 18(1):50–60
Marimon R, McGrattan E, Sargent TJ (1990) Money as a medium of exchange in an economy with artificially intelligent agents. J Econ Dynam Control 14(2):329–373
Menger K (1892) On the origin of money. Econ J 2(6):239–255
Muth JF (1961) Rational expectations and the theory of price movements. Econom J Econom Soc 29(3):315–335
Nosal E, Rocheteau G (2011) Money, payments, and liquidity. MIT press
Oh S (1989) A theory of a generally acceptable medium of exchange and barter. J Monet Econ 23(1):101–119
Osborne M (2016) Exponential versus hyperbolic discounting: a theoretical analysis. SSRN 2518162.
Palminteri S, Lefebvre G, Kilford EJ, Blakemore S-J (2017) Confirmation bias in human reinforcement learning: Evidence from counterfactual feedback processing. PLoS Comput Biol 13(8):e1005684
Rietz J (2019) Secondary currency acceptance: experimental evidence with a dual currency search model. J Econ Behav Organization 166:403–431
Roth AE, Erev I (1995) Learning in extensive-form games: experimental data and simple dynamic models in the intermediate term. Games Econ Behav 8(1):164–212
Shi S (1995) Money and prices: a model of search and bargaining. J Econ Theory 67(2):467–496
Sutton RS, Barto AG (1998) Reinforcement learning: an introduction. Vol. 1. MIT Press, Cambridge
Van Den Bos W, Cohen MX, Kahnt T, Crone EA (2012) Striatum-medial prefrontal cortex connectivity predicts developmental changes in reinforcement learning. Cerebral Cortex 22(6):1247–1255
Wanner D (2014) Serious economic games: designing a simulation game for an economic experiment. In International conference of design, user experience, and usability. Springer, pp 782–793
Wright R (1995) Search, evolution, and money. J Econ Dynam Control 19(1–2):181–206
Wulff DU, Mergenthaler-Canseco M, Hertwig R (2018) A meta-analytic review of two modes of learning and the description-experience gap. Psychol Bull 144(2):140
Acknowledgements
This work was supported by the Agence Nationale de la Recherche (ANR-16-CE38-0003). The funders had no role in study design, data collection, and interpretation, or the decision to submit the work for publication.
Author information
Authors and Affiliations
Contributions
AN and BG wrote the code, performed the experiments and the data analysis; AN, BG, GL, TB, NR, and SB-G. designed the study and co-wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nioche, A., Garcia, B., Lefebvre, G. et al. Coordination over a unique medium of exchange under information scarcity. Palgrave Commun 5, 153 (2019). https://doi.org/10.1057/s41599-019-0362-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-019-0362-2