Abstract
Humans require multiple natural resources for their wellbeing and assign different portions of their efforts to secure resources due to their limited time and energy. When one resource is scarce, it may be replaced with a substitute which may fully or partially cover the shortage. However, existing research of coupled natural-human systems (CNHS) usually focuses on a single resource and misses these aspects. To fill the gaps, we question: how would substitutability and effort asymmetry influence system responses, resource management, and sustainability? Building on an existing conceptual framework, we developed a CNHS model with two resources and infrastructures in a centralized governance structure. Model analysis showed that substitutability and effort asymmetry significantly influence policy flexibility, performance, and sustainability of the coupled system, thereby highlighting challenges and offering insights in governing systems with multiple resources.
Similar content being viewed by others
Introduction
Human societies require many elements to function properly—including natural resources, energy, technology, infrastructure, and so on—each of which has its own dynamics, interacts with one another, and co-evolves in a complex way (Liu et al., 2007). Humans particularly take a special role as both a consumer and provider of resources in the societies. This double-edged role creates dilemmas between short-term profits as a consumer and long-term wellbeing as a provider because natural resources are limited (Ostrom, 2015). Besides, public infrastructure (PI) engages in human-natural interactions and creates new interactions to both humans and nature. Here, PI can be categorized as either hard or soft: hard infrastructure has a physical form (e.g., canal, levee, and dam), whereas soft infrastructure is intangible (e.g., social norm, rule, and institution). Many traditional studies of such coupled natural-human systems (CNHS), e.g., traditional bioeconomic models of resource management, however, have overly simplified interactions between human and natural systems (Liu et al., 2007). Recognizing interdependence among humans, natural systems and PI, recent CNHS studies integrate these elements more explicitly, leading to new insights and providing new pathways to the research on natural resource management and sustainability of CNHS (Kates et al., 2001; Redman et al., 2004; Ostrom, 2009; Chen and Perc, 2014).
Under the co-evolutionary perspective, a number of new frameworks and models of CNHS have been developed. For example, Anderies et al. (2004) established a conceptual framework between humans, PI, and natural resource on the basis of empirical case studies (Fig. 1a). Others have developed a variety of models to study system responses and how to manage CNHS in more sustainable ways: stylized modeling (Satake et al., 2007; Cifdaloz et al., 2010; Anderies et al., 2013; Yu et al., 2015; Muneepeerakul and Anderies, 2017), network-based modeling (Lade et al., 2016; Barfuss et al., 2017) and agent-based modeling (Brown et al., 2008; Yu et al., 2009; Pérez et al., 2016; Khan et al., 2017), each with its own pros and cons (Blair and Buytaert, 2015; Müller-Hansen et al., 2017).
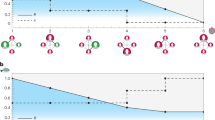
A framework capturing interactions between natural resources, RUs, public infrastructure provider (PIP) and public infrastructure. a an existing framework with a single resource condition (Anderies et al., 2004), b a modified framework with two resources, each of them having its respective infrastructure. Dash-lined entities and interactions are newly added from (a). RUs invest their time and effort to natural resources and harvest resources for their living in return (Link 1). RU’s work is not only farming but also participating in the maintenance of PI for their wellbeing (Link 3). RUs also agree to policies established by PIP, paying tax to PIP in the amount proportional to their harvest (Link 2). A certain portion of the tax is invested to PI for its maintenance to sustain the system (Link 5)
Substitutability, asymmetry, and sustainability of CNHS
In many of these models, humans are assumed to rely on one resource. Human societies, of course, require more than one type of resource and their wellbeing depends on these resources to varying degrees (Joyce et al., 2009; Hansson and Mokeeva, 2015). Once faced with a scarcity of one resource, resource users (RUs) may decide to substitute that resource with other resources of similar functionality.
Substitutability is an ability to replace one product, technology or service which is insufficient, to another (Hritonenko and Yatsenko, 2013). It has been widely used in economics to understand an elasticity of substitution between human and natural capitals. The concept has also been expanded to include other situations (Bordeaux et al., 2005): human-natural capital substitution, natural capital-energy substitution (Markandya and Pedroso-Galinato, 2007), import-export goods substitution (Obstfeld and Rogoff, 2000), and information technology-labor substitution (Dewan and Min, 1997). Substitutability is an important part of the sustainability discourse (Gerlagh and Van der Zwaan, 2002; Pezzey and Anderies, 2003; Traeger, 2011; Fenichel and Zhao, 2015; Baumgärtner et al., 2017; Pezzey and Toman, 2017), in particular in the context of weak vs. strong sustainability (Ayres et al., 1998; Neumayer, 2003).
Due to their limited time and energy, RUs may distribute varying degrees of their effort to harvest different resources. RUs may spend more effort on one resource (effort asymmetry) or allocate the same amount of effort on two resources (effort symmetry). RUs’ decision on such symmetry/asymmetry in effort clearly has significant consequences on the dynamics of the resources and, through feedbacks, other components of CNHS.
The value of the present work is derived from its explicit focus on dynamical interactions between substitutable resources, resource-specific infrastructure, and their management. Some of the previous body of work had either, but not all, of these elements (Anderies, 2003; Pezzey and Anderies, 2003; Fenichel and Zhao, 2015); some previous works considered some of these elements, but not in a dynamical fashion (Ayres et al., 1998; Gerlagh and Van der Zwaan, 2002; Traeger, 2011; Baumgärtner et al., 2017). These dynamical interactions can result in a noticeable difference to our understanding of the system responses to shocks, related to system sustainability in the long term. Indeed, recent research has raised questions about interactions and tradeoffs between multiple resources (Schlüter et al., 2012; Qubbaj et al., 2014; Kramer et al., 2017). In this sense, we build on a recent CNHS model and aim to address the following question: How do substitutability of multiple resources and asymmetry of users’ effort shares influence the general response, governance/management, and sustainability of CNHS?
System design
We formulate a mathematical model of RUs, public infrastructure provider (PIP), natural resources and PIs to find out how substitutability and effort asymmetry affect the general response, governance/management, and sustainability of CNHS. The model is built on the model developed in Muneepeerakul and Anderies (2017), with the key difference being the inclusion of a second resource (R2) and R2-specific PI (PI2) as Fig. 1b. A summary of key parameters and variables are provided in Table 1.
Adding substitutability and asymmetry to a CNHS model
Under the setting of two resources and two resource-specific PIs (see Fig. 1b), RUs decide how to distribute their effort to each resource due to their limited time and energy. The two resource-specific PIs are assumed to be governed by a single PIP, i.e., mimicking centralized governance structure. Consequently, the interactions between the two resource-PI subsystems are indirectly linked by the behavior of RUs and the policy of PIP (to be distinct from cases in which the two resources interact directly as in predator-prey situations). Specifically, the effects of substitutability and asymmetry are captured in a utility calculation, which makes use of CES (constant elasticity of substitution) production function. CES production function has traditionally been used for analyzing conditions of natural or human capitals in economics, and its generic form is as follows:
where α (0 ≤ α ≤ 1) and β (β ≤ 1) (these are the ranges of values that make sense economically (Kemfert, 1998; Markandya and Pedroso-Galinato, 2007) capture the effects of asymmetry and substitutability, respectively. α reflects how much RUs distribute their effort shares on one resource (in this case, Resource 1 with a payoff X1) to derive their wellbeing. When α equals 0.5, the effort shares are symmetric: RUs distribute the same amount of time or energy on two resources. Asymmetry occurs when α increases or decreases from 0.5. When α is one or zero, RUs only work with Resource 1 or 2, i.e., the single-resource setting is resumed. Our model does not simulate these conditions because substitutability and asymmetry are irrelevant when only one resource exists. β describes how substitutable two resources are. β is 1 if two resources are perfectly substitutable, and substitutability between the two reduces with smaller or negative β values.
An intriguing aspect is that RUs can observe the asymmetry in efforts of other RUs and adjust their own, through such mechanisms as replicator dynamics or optimization. To keep the dimensionality of the model low and its result interpretation clear, α is currently treated as a parameter in the present analysis, but such dynamical aspects of α call for additional future analyses.
Natural resource dynamics
There are two resources (R1 and R2) in this model, whose dynamics are captured by the following equations:
where Gi(Ri) is the natural process of resources, and Ai(Ri, Ii, U, αi) is the harvest of natural resources by RUs. Gi(Ri) is assumed to take a simple form of g −lRi, where g is the natural growth rate of resources and l is the natural death rate of resources. To highlight the interactions between different entities and facilitate result interpretation, we set g and l of the two natural resources to be identical. This configuration prevents individual characteristics of natural resources to become a main driver of the results. The amount of RUs’ Resource i harvest is proportional to the number of RUs (N), a fraction of time RUs participate inside the system (U), levels of natural resources (Ri), productivity of PI per person (Hi(Ii)), and how much RUs share their effort to different resources (αi; α1 = α, α2 = 1−α). Putting them all together, we obtain that Ai(Ri, I, U, αi) equals αiUNRiHi(Ii).
Public infrastructure dynamics
In this model, public infrastructure PI1 and PI2 are specific to Resources 1 and 2, respectively. Each PI is not directly involved in the other resource, and its state (represented by variables I1 and I2) individually changes over time. PIs naturally age over time and require continuous maintenance by the participation of RUs. Then,
where Mi(Ri, Ii, U, αi) is the maintenance of each PI by the PIP, and δ is a natural decay rate of PIs. PIs are sustained well when the PIPs invest a large enough portion from tax, and RUs sufficiently harvest natural resources. Mi(Ri, Ii, U, αi) will be explained in the social dynamics section below. All the parameters of PI1 and PI2 are the same, again, to highlight the interactions between different entities and facilitate result interpretation. Note that PIs are not directly coupled to each other; they are indirectly coupled through decision-making processes of the PIP and RUs. I1 and I2 are then mapped into a productivity-related term through the productivity function Hi(Ii):
where h is a maximum harvest productivity per person. Most PIs do not function when their states are less than a certain threshold (I0). Moreover, there is usually the limit to the productivity of PI, which is assumed to remain the same after the state reaches a threshold (Im).
Social dynamics and decision-making
To capture the social evolution, we make use of several established equations and relationships from social science to mathematically define social responses and decision-making dynamics. For RUs, replicator equations–from evolutionary game theory (Muneepeerakul and Anderies, 2017)–and CES production function are combined to model changes in the RUs’ behaviors.
A generic form of the replicator equation for a frequency of strategy i (xi) is \(\dot x_i = x_i\left( {\pi _i - \phi } \right)\), where πi is a payoff a user earns from strategy i, and ϕ is an averaged payoff. In this model, RUs have two options: to stay inside the system by participating in crop farming (U) with a payoff πU and to work outside the system (W; U+W = 1) with a wage w (=πW). When working inside the system, a RU must pay a fraction C of farming revenue to the PIP (Link 3 in Fig. 1). Then, the replicator equation for our model is as follows:
When multiple natural resources have substitutable relations, the calculation of πU is not simply the sum of each natural resource revenue. It is here where we incorporate the concept of substitutability from economics through CES production function.
In this paper, we focus on the effects of α and β in the production function, which represent degrees of effort asymmetry and substitutability, respectively. Specifically, we write πU as follows:
where piRiHi(Ii) is a payoff which RUs earn from resource i.
Maintenance of infrastructure i (Mi(Ri,Ii,U,αi)) is assumed to depend on various factors described in preceding paragraphs. First, it depends on how much income RUs extract from resource i, namely αipUNRiHi(Ii). RUs then contribute a fraction C (which is decided on by the PIP) of this income to the PIP. The PIP decides on what fraction yi of these RU contributions will be invested in the maintenance of infrastructure i. Finally, the maintenance function of PIi is Mi(Ri, Ii, U, αi) = μyiCαipUNRiHi(Ii), where μ is an efficiency parameter of PIP investment. The payoff of PIP is πPIP = CpUN[(1 − y1)αR1H1(l1) + (1 − y2)(1 − α)R2H2(I2)].
Coupled dynamics
To address our research questions, we conduct numerical simulations (trapezoidal numerical approximation) of the above dynamical model with combinations of policy parameters (y1, y2 and C) for a wide range of substitutability (β) and asymmetry (α) settings. We then analyze the results for cases in which the coupled system is sustained in the long run or collapses at different degrees of shocks to Resource 1. To clearly see the interplay between disturbance, effort asymmetry, substitutability, system performance, and sustainability, we run the simulations long enough, until the system is stabilized. Then, we subject the system to a shock in the form of a drop in the availability of Resource 1. By applying shocks only to Resource 1, our analysis highlights the roles played by the substitutability and asymmetry of natural resources.
Defining sustainability and viable policy for CNHS
In what follows, CNHS is said to be “sustained in the long run” if the following conditions are met: 1) Some RUs remain in the system and participate in resource-related labors (U* > 0), and 2) Investing in the maintenance of PIs to sustainably manage natural resources is more profitable for PIP than the alternative option (πP ≥ wP), ensuring sufficient incentives for the PIP to participate in the system. In other words, these definitions state that both types of social agents (RUs and PIP) must be sufficiently satisfied for the system to be “sustained in the long run”.
For given α and β values, a large number of y1, y2 and C combinations (132,651 in total)—the combination {y1, y2, C} a policy (see Table 1)—are prescribed to the system. The policies that satisfy the two sustainability conditions above—which we dub “viable policies”—constitute a “cloud” in the y1−y2−C policy space (see Fig 2a–c). In certain parts, both I1 and I2 are functioning, but in others, only one of either I1 or I2 functions. Only I1 functions in all cloud points when α is close to one, only I2 functions in all cloud points when α is close to zero (see Fig. 2a), and both I1 and I2 function in all cloud points when α is 0.5 (see Fig. 2c). As α moves from 0.5 (symmetric condition) to either of its extremes close to 0 or 1 (asymmetric conditions), the viable-policy cloud bifurcates into two clusters, one of which includes policies corresponding to only one functioning PI.
a a viable policy cloud in y1-y2-C policy space at α = 0.1 (extremely asymmetric condition), β = 1 (highly substitutable condition) and no disturbance case. b a viable policy cloud in y1-y2-C policy space at α = 0.3 (moderately asymmetric condition), β = 1 and no disturbance case. c a viable policy cloud in y1-y2-C policy space at α = 0.5 (symmetric multiple-resource condition), β = 1 and no disturbance case. d 3D bar graph which sums up the points in policy clouds on behalf of policy flexibility for every α and β combination. Each red box represents the number of points inside the clouds in (a–c). Color bars for (a), (b) and (c) are payoffs of PIP in each y1-y2-C policy design. The blue dots are projections of the clouds to y1-y2, y1-C and y2-C planes
Sustainability of CNHS is also relevant to uncertain disturbances. The world does not simply stay in the equilibriums but is often perturbed by various external forces: natural (e.g., floods, droughts, earthquakes, etc.) or social forces (e.g., price changes, migration, policy changes, etc.) (Anderies et al., 2004). In this research, we drop a state of one resource (Resource 1) to certain levels to directly evaluate sustainability when one resource is in short. A policy design which seemed to be “viable” may fail when disturbed. We analyze whether CNHS is still well-sustained after experiencing disturbances, making a comparison to cases without any shock.
Results and analysis
Substitutability, asymmetry, and flexibility in policy design
A volume of policy cloud (the number of discrete y1, y2 and C combination points) reflects the number of viable policies (NVPtotal). NVPtotal is a sum of NVPeither and NVPboth: NVPeither is the number of viable policies that maintain only one of the two PIs, whereas NVPboth is the number of viable policies that maintain both PIs. The greater NVPtotal signifies that PIP is more flexible in policy decisions as PIP has a broader range of policy selection to successfully maintain the system. Figure 2d exhibits how varying α and β influence the NVPtotal.
NVPtotal generally increases with higher β as one resource can easily replace the other. Effort symmetry/asymmetry, on the other hand, affects NVPtotal differently at varying degrees of substitutability—which changes the necessity of maintaining both PIs. Asymmetry increases NVPeither when the two resources are relatively substitutable (see Fig. 3a, red bars) and decreases NVPboth (see Fig. 3a, blue bars). For viable policies under which only one PI is sustained, higher asymmetry indicates a smaller waste of effort spent on the other, collapsing the sustained PI. When both PIs are sustained, policies with the lop-sided effort allocation of RUs are likely to fail due to the imbalanced effort shares for the maintenance of the two PIs. In aggregate, effects of symmetry/asymmetry collectively lead to the W-shaped relationship between NVPtotal and α in a substitutable condition (say, β > 0): the lowest when the effort is allocated moderately asymmetric (α = 0.3, 0.7), and increasing when effort share on resources is either symmetric (α = 0.5) or extremely asymmetric at both ends of α (α close to 0 or 1). In contrast, weak substitutability (or complementarity), e.g., when β < 0, modifies the effect of effort asymmetry on NVPtotal, especially on those policies that sustain only one PI (see Fig. 3). As a result, decreasing β leads to great NVPtotal declines in extremely asymmetric cases. In this condition, the resource with collapsed PI cannot be substituted by another resource, and such policies can no longer sustain CNHS. On the other hand, the effect of decreasing β is smaller when both PIs function (and both resources are thus sufficiently harvested to support RUs). Together, these effects gradually turn the NVPtotal-α relationship from the W shape to a unimodal bell-like curve when substitutability is low (see Figs 2d and 3).
The relationship between NVP and α when the two resources are perfectly substitutable (a: β = 1), and when they are rather complementary to each other (b: β = −1). In this figure, the NVP is categorized into two groups: those that sustain both PIs (NVPboth; blue bars) and those that sustain only one PI (NVPeither; red bars). The sum of two groups at each α value is NVPtotal
Moreover, the relationship between substitutability, asymmetry, and NVPtotal varies with disturbance levels (see Fig. 4). At a weak disturbance (Fig. 4a), the α-β-NVPtotal relationship does not noticeably differ from that in cases without any disturbance (Fig. 2d). However, the relationship becomes skewed when the disturbance levels are high (see Fig. 4b–d). The skewness originates from the asymmetric effort shares on two resources and the fact that disturbance is imposed only Resource 1 (precisely to highlight the effects of substitutability and asymmetry). When α is close to one, RUs are highly dependent on Resource 1, and large disturbances on Resource 1, therefore, critically degrade NVPtotal. CNHS is still sustained mostly by replacing a drop of Resource 1 with a substitutable resource (Resource 2). When α is small, RUs are less dependent on Resource 1, and NVPtotal is largely insensitive to disturbances on Resource 1.
Substitutability, asymmetry, and system performance
That the system is sustained in the long run does not necessarily imply that it performs well. To investigate this aspect, we use the infrastructure conditions as a proxy of the system performance: well-maintained, high-capacity infrastructure indicates that social agents strongly engage in the system, which further indicates that they derive good wellbeing/utility from the system. In particular, we calculate the expected values of I1 and I2 at steady state (E[I1] and E[I2]), resulting from all viable policies for different combinations of α and β values (see Fig. 5).
Expected values of infrastructure states for I1 and I2 (E[I1] and E[I2]), averaged across all viable policies, as functions of α and β in two disturbance levels. If no viable policy exists (NVPtotal = 0), the expected performance is set to zero as no infrastructure functions. a E[I1] when R1 is not disturbed. b E[I2] when R1 is not disturbed. c E[I1] when R1 experiences 60% disturbance. d E[I2] when R1 experiences 60% disturbance
PI1 collapses when α is either low or high (i.e., 0.1 and 0.9) and the resources are not substitutable (β < 0) (see Fig. 5a); the collapse is depicted as the “abyss” in the “system performance landscape” of Fig. 5. In other cases where PI1 does not collapse, the effect of substitutability appears rather small when RUs distribute effort shares symmetrically (α = 0.5) but becomes significant when effort shares are quite asymmetric (see α of 0.8 and 0.9). The expected performance of PI1, E[I1], is higher for greater α values in highly substitutable conditions as RUs place a greater priority on harvesting Resource 1 (the far right corners of the panels in Fig. 5; α > 0.5, β > 0). In these cases of high substitutability, a viable policy can afford not to maintain PI2 too much because RUs’ wellbeing/utility can be maintained by making sure that enough of Resource 1 is being harvested (RUs already put more efforts on Resource 1; α > 0.5); this explains the collapse of PI2 under these settings (Fig. 5b). With low substitutability (the halves closer to the reader in the panels of Fig. 5; β < 0), RUs need both resources. Here, effort asymmetry leads to lower wellbeing and, in turn, lower contributions toward maintenance of PIs. This explains the declines in both E[I1] and E[I2] as α moves away from symmetry in either direction.
Disturbances modify the relationship between substitutability, asymmetry, and performance. Figure 5c, d show E[I1] and E[I2] when the system is subject to a 60% one-time drop in Resource 1. The abyss areas—corresponding to infrastructure collapse—expand for both E[I1] and E[I2], despite the fact that the disturbance only affects Resource 1 directly. This highlights the coupled and intertwined nature of CNHS. Interestingly, while the shock generally causes E[I1] and E[I2] to decrease, E[I1] increases at high α and high β, i.e., when RUs focus their effort on Resource 1 and the two resources are relatively substitutable. This results from the fact that in these settings, for a policy to be viable, it must maintain PI1 in an even greater shape so that the system can absorb the effects of the shock, hence an increase in E[I1]. All in all, the irregular shapes of Fig. 5 reflect the complex interplay among substitutability, asymmetry, and performance, as well as the complex governance landscape that we have to navigate.
Discussion
CNHS dynamics are nonlinear and multi-dimensioned. Complexities are embedded in various entities and their interactions, making it hard to fully understand such systems. This paper incorporates concepts of substitutability and asymmetry into a CNHS model to gain insights into how these properties affect policy flexibility, system performance, and sustainability and how these effects change in the face of disturbances. Our analysis thus focuses on policy flexibility and system performance, not what the best policy is, because the goal of governing such systems can be multi-faceted and labeling a specific set of y1, y2 and C to be a “best” policy is controversial at best and misleading at worst.
Our results show that substitutability and asymmetry are not separate concepts, but the interplay with each other. The relationship between asymmetry on policy flexibility is W-shaped in high substitutability but is bell-shaped in low substitutability (Figs 2d and 3), and disturbances can alter this relationship (Fig. 4). Among the policies that result in a sustainable outcome, PIs may be in a poor or great shape—another facet that needs to be taken into account (Fig. 5). Due to the coupled nature of the system, disturbances affecting one resource can affect the performance of the other resource’s infrastructure. All these results emphasize the rich dynamics of and challenges in governing a CNHS with multiple resources—which is to say the system in which we live. As such, multiple resources and their interactions need to be implemented to future CNHS models for us to manage these systems successfully.
This paper contributes to a deeper and more nuanced understanding of the dynamics of CNHS and provides fertile ground for several future research directions. An intriguing direction to treat α as a dynamical variable instead of a constant parameter to reflect how real-world RUs may adjust α based on their environmental and social conditions. Another direction is to compare centralized and decentralized governance structures. Our model is confined to a centralized governance structure with one PIP, but in reality, each resource-specific PI may require its own separate PIP. In this case, there will be interactions between the PIPs and interactions between the PIPs and other elements. These are just two examples out of many future directions that will enrich our understanding and ability to tackle more complex and realistic CNHS.
Data availability
Computational simulation datasets from the model are available from the authors upon request.
References
Anderies JM (2003) Economic development, demographics, and renewable resources: a dynamical systems approach. Env Dev Econ. https://doi.org/10.1017/s1355770x0300123
Anderies JM et al. (2013) Aligning key concepts for global change policy: robustness, resilience, and sustainability. Ecol Soc. https://doi.org/10.5751/ES-05178-180208
Anderies JM, Janssen MA, Ostrom E (2004) A framework to analyze the robustness of social-ecological systems from an institutional perspective. Ecol Soc. 9(1):18
Ayres RU, Van Den Bergh JC, Gowdy JM (1998). Viewpoint: weak versus strong sustainability. In: Tinbergen Institute discussion papers. Tinbergen Institute, Amsterdam, The Netherlands, p 98–103
Barfuss W et al. (2017) Sustainable use of renewable resources in a stylized social-ecological network model under heterogeneous resource distribution. Earth Syst Dyn. https://doi.org/10.5194/esd-8-255-2017
Baumgärtner S, Drupp MA, Quaas MF (2017) Subsistence, substitutability and sustainability in consumption. Environ Resour Econ. https://doi.org/10.1007/s10640-015-9976-z
Blair P, Buytaert W (2015) Modelling socio-hydrological systems: a review of concepts, approaches and applications. Hydrol Earth Syst Sci Discuss. https://doi.org/10.5194/hessd-12-8761-2015
Bordeaux L et al. (2005) When are two web services compatible? In: Shan M, Dayal U, Hsu M (eds), Technologies for E-Services, 5th International Workshop, TES 2004. Vol 3324 of Lecture Notes in Computer Science. p 15–28. https://doi.org/10.1007/978-3-540-31811-8_2
Brown DG et al. (2008) Exurbia from the bottom-up: Confronting empirical challenges to characterizing a complex system. Geoforum. https://doi.org/10.1016/j.geoforum.2007.02.010
Chen X, Perc M (2014) Excessive abundance of common resources deters social responsibility. Sci Rep. https://doi.org/10.1038/srep04161
Cifdaloz O et al. (2010) Robustness, vulnerability, and adaptive capacity in small-scale social-ecological systems: The pumpa irrigation system in Nepal. Ecol Soc. 15(3):39
Dewan S, Min C (1997) The substitution of information technology for other factors of production: a firm level analysis. Manag Sci 43(12):1660–1675
Fenichel EP, Zhao J (2015) Sustainability and substitutability. Bull Math Biol. https://doi.org/10.1007/s11538-014-9963-5
Gerlagh R, Van der Zwaan BCC (2002) Long-term substitutability between environmental and man-made goods. J Environ Econ Manag. https://doi.org/10.1006/jeem.2001.1205
Hansson R, Mokeeva E (2015) Securing resilience to climate change impacts in coastal communities through an environmental justice perspective: a case study of Mangunharjo. Indonesia Robin Hansson, Semarang
Hritonenko N, Yatsenko Y (2013) Mathematical modeling in economics, ecology and the environment. Kluwer Academic Publishers, Dordrecht, Netherlands
Joyce LA et al. (2009) Managing for multiple resources under climate change: National forests. Environ Manag. https://doi.org/10.1007/s00267-009-9324-6
Kates RW et al. (2001) Environment and development: sustainability science. Science. https://doi.org/10.1126/science.1059386
Kemfert C (1998) Estimated substitution elasticities of a nested CES production function approach for Germany. Energy Econ. 20(3):249–264. https://doi.org/10.1016/S0140-9883(97)00014-5
Khan HF et al. (2017) A coupled modeling framework for sustainable watershed management in transboundary river basins. Hydrol Earth Syst Sci. https://doi.org/10.5194/hess-21-6275-2017
Kramer DB et al. (2017) Top 40 questions in coupled human and natural systems (CHANS) research. Ecol Soc. https://doi.org/10.5751/ES-09429-220244
Lade SJ et al. (2016) Modelling social-ecological transformations: an adaptive network proposal. arXiv. https://doi.org/10.1186/1475-2875-11-226
Liu J et al. (2007) Complexity of coupled human and natural systems. Science. https://doi.org/10.1126/science.1144004
Markandya A, Pedroso-Galinato S (2007) How substitutable is natural capital? Environ Resour Econ 37(1):297–312. https://doi.org/10.1007/s10640-007-9117-4
Müller-Hansen F et al. (2017) Towards representing human behavior and decision making in Earth system models—an overview of techniques and approaches. Earth Syst Dyn. https://doi.org/10.5194/esd-8-977-2017
Muneepeerakul R, Anderies JM (2017) Strategic behaviors and governance challenges in social-ecological systems. Earth’s Future. 5(8):865–876. https://doi.org/10.1002/2017EF000562
Neumayer E (2003) Weak versus strong sustainability—Exploring the limits of two opposing paradigms. Edward Elgar Publishing Limited, Cheltenham, UK
Obstfeld M, Rogoff K (2000) The six major puzzles in international macroeconomics: is there a common cause? NBER/Macroecon Annu. 15(1):339–390. https://doi.org/10.1162/08893360052390428
Ostrom E (2009) A general framework for analyzing sustainability of social-ecological systems. Science. https://doi.org/10.1126/science.1172133
Ostrom E (2015) Governing the commons: The evolution of institutions for collective action. Cambridge University Press, Cambridge
Pérez I, Janssen MA, Anderies JM (2016) Food security in the face of climate change: adaptive capacity of small-scale social-ecological systems to environmental variability. Glob Environ Change. https://doi.org/10.1016/j.gloenvcha.2016.07.005
Pezzey JCV, Anderies JM (2003) The effect of subsistence on collapse and institutional adaptation in population-resource societies. J Dev Econ. https://doi.org/10.1016/S0304-3878(03)00078-6
Pezzey JCV, Toman MA (eds) (2017) The economics of sustainability. 1st edn. Ashgate, Routledge, Aldershot, UK
Qubbaj MR, Shutters ST, Muneepeerakul R (2014) Living in a network of scaling cities and finite resources. Bull Math Biol. https://doi.org/10.1007/s11538-014-9949-3
Redman CL, Grove JM, Kuby LH (2004) Integrating social science into the Long-Term Ecological Research (LTER) Network: Social dimensions of ecological change and ecological dimensions of social change. Ecosystems. https://doi.org/10.1007/s10021-003-0215-z
Satake A et al. (2007) Synchronized deforestation induced by social learning under uncertainty of forest-use value. Ecol Econ. https://doi.org/10.1016/j.ecolecon.2006.11.018
Schlüter M et al. (2012) New horizons for managing the environment: a review of coupled social-ecological systems modeling. Nat Resour Model. https://doi.org/10.1111/j.1939-7445.2011.00108.x
Traeger CP (2011) Sustainability, limited substitutability, and non-constant social discount rates. J Environ Econ Manag. https://doi.org/10.1016/j.jeem.2011.02.001
Yu C et al. (2009) Integrating scientific modeling and supporting dynamic hazard management with a GeoAgent-based representation of human-environment interactions: a drought example in Central Pennsylvania, USA. Enviro Model Softw. https://doi.org/10.1016/j.envsoft.2009.03.010
Yu DJ et al. (2015) Effect of infrastructure design on commons dilemmas in social−ecological system dynamics. Proc Natl Acad Sci. 112(43):13207–13212. https://doi.org/10.1073/pnas.1410688112
Acknowledgements
The research reported in this paper was supported in part by the Army Research Office/Army Research Laboratory under award #W911NF1810267 (Multi-University Research Initiative). The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies either expressed or implied of the Army Research Office or the U.S. Government.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Oh, W.S., Muneepeerakul, R. How do substitutability and effort asymmetry change resource management in coupled natural-human systems?. Palgrave Commun 5, 80 (2019). https://doi.org/10.1057/s41599-019-0289-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1057/s41599-019-0289-7