Introduction

Group formation is an inherent and fundamental activity in every human society. Human jointly form various groups to cooperate for their survival and compete with other groups, for living in a group provides individuals with potential benefits such as shared duties, protection from outsiders, and efficiency of resource exploitation (Clutton-Brock, 2002; Pulliam and Caraco, 1984; Bertram, 1978; Clark and Mangel, 1986). In this sense, there have been intense game-theoretic researches on how coalition forms and are organized to conduct diverse activities (Demange and Wooders, 2005). One of major difficulties in studying group formation in a competitive situation lies in i) nonlinearity and nonmonotonicity of group-size effects and ii) complex nature of aggregation dynamics.

The benefits of forming groups tends to grow increasingly with group size: a group with twice as many members can easily earn more than twice. For example, collaborations through a division of labour in a large group can be more efficient and systematic than in a small group, rendering the large group more competitive in a contest. Also, the large group is associated with greater diversification of specific risks, which leads to economic benefits (Cassidy et al., 2015; Harris, 2010; Kitchen et al., 2004; Markham et al., 2012; Palmer, 2004; Scarry, 2013). However, there are also negative nonlinear effects of group size. For instance, bureaucratic inefficiency in overall group management tends to grow faster with group size: establishing communication and cooperation between members becomes a challenging task in the large group (Brym and Lie, 2006; Olson, 2009; Nosenzo et al., 2015). Resource allocation in the large group is likely to be less efficient than in the small group (Krause, 1994; Bednekoff and Lima, 2004). These negative effects will suppress emergence of excessively large groups. Thus, taking into account these nonlinear positive and negative effects of group size, people make decision on merging, leaving, and creating their new groups in order to maximize their shares.

Besides the nonlinear and nonmonotonic group-size effects, what makes it difficult to study the group formation is the complex nature of aggregation dynamics resulting from the fact that members' shares in a group depend not only on their own group’s size, but also on other groups’ sizes. Especially in game theory, finding a stationary distribution of aggregation has been dealt as a fundamental problem (Hart and Kurz, 1983; Bernheim et al., 1987; Bloch, 1996; Sanchez-Pages, 2007). In Hart and Kurz (1983), strong equilibrium is suggested as the notion for stability of a coalition structure in which no group of players, whether from the same coalition or from different ones, can get together and form new coalition(s) in such way that they are all better off. There have been several attempts to modify the equilibrium concept to allow more various group formations at equilibrium, such as "coalition-Proof Nash equilibrium" which requires self-enforcing agreements among group of players in (Bernheim et al., 1987). However, although the strong Nash equilibrium and its variations provide a robust and appealing stability concept, they are too restrictive and may rarely exist in many situations.

In this paper, we develop a minimal group formation model to study the dynamics of group formation with consideration for the group-size effects, and show various group distributions and resource allocations appearing as our equilibrium outcomes. Our work consists of two parts: (i) constructing an individual payoff function that reflects the group-size effects and (ii) introducing aggregation dynamics that induces reasonable stationary distributions.

The study focuses on how resource allocations and social inequalities can be attributed to the counteracting group-size effects within aggregation dynamics. For doing this, we differentiate the inequality between groups from that between individuals. For example, we can observe, from the model, that a group of 20% of population takes 80% of the whole resource in a certain case, as stated in the Pareto principle. However, this does not necessarily imply that there is as much rich-poor gap exists between individuals. This discrepancy is due to interaction between the two (positive and negative) size effects, and makes it hard for a social planner to achieve economic efficiency and equality.

Within the context of the model, the social planner can control resource allocation through adjusting the both positive and negative group-size effects. The positive effect may be reduced by setting a limit to the maximum resource that can be taken by a single group. Implementing regulations to support relatively small groups in a contest is another way to reduce the positive effect. On the contrary, assigning a penalty directly according to group size, like imposing a progressive tax, results in enhancing the negative size effect. While the both approaches are to suppress emergence of excessively large groups, reducing the positive effect and enhancing the negative one are subtly different. This paper differentiates it and investigates under what condition common social inequalities are created, such as the Pareto principle and social polarization. Especially, we want to specify range of the size effects where social equalities at both group and individual levels can be achieved.

Since the payoff function we develop is very simple and works for general cases, there is often no Nash-type equilibrium unless further constraints on group dynamics is assumed. The approach taken in this work is based on an observation for large population that people take a conservative strategy when uncertainty is high (Machina, 1992). Since the number of all possible combinations of group formation increases explosively with population size and thus it is not plausible for each individual to evaluate all options, we rather assume that people take a conservative strategy to reduce their possible maximum loss, sequentially creating groups. Besides that this sequential maximin strategy may reflect more realistic behaviour in large population, another benefit of the approach is that the corresponding stationary equilibriums always exist and are easily computable.

Size effects in contests

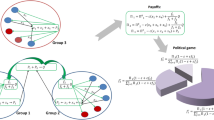
We consider a contest situation in which N players vie for getting a resource R. Let G = (n1,…,nK) denote a group distribution which is K disjoint partitions of N persons satisfying \(\mathop {\sum}\nolimits_{i = 1}^K n_k = N\). The normalized group distribution with respect to the total population is \(\overline G = \left( {\overline n _1, \cdots ,\overline n _K} \right)\) where \(\overline n _i = n_i/N\). Let gk be the share of group k and \(\mathop {\sum}\nolimits_{i = 1}^K g_k = R\). Similarly, the normalized group share is \(\overline g _i = g_i/R\).

In intergroup contests among group-living animals, group size is a common measure of resource-holding potential and a group’s chances of winning increases with its size roth. In order to describe the group's gaining under such size effect, we adopt Tullock-form (or logit-form) contest success function as a rule of dividing the resource among the groups.Footnote 1 Specifically, Group k obtains the following share of the resource:

$$g_k\left( G \right) = R\frac{{n_k^\alpha }}{{\mathop {\sum}\limits_{i = 1}^K n_i^\alpha }},\,{\kern 1pt} \alpha \ge 1.$$
(1)

As seen in (1), the share for each group depends on the size of that group and those of the other groups as well.

The parameter α is an exponent of a positive size effect, which represents the degree of effectiveness of the group size in the contest. For α = 1, the share of each group is proportional to the relative size of the group to the sum of all groups' sizes. For α > 1, \(n_k^\alpha\) exhibits increasing returns to scale and the size of each group has a greater effect on its share than for α = 1.

The members in a group equally share their group's gain.Footnote 2 Let πk represent the payoff for each player in group k. It is then defined as follows, given a group distribution G = (n1,…,nK):

$$\pi _k\left( G \right) = g_k\left( G \right)\frac{1}{{n_k^\beta }},\,\beta \ge 1$$
$$= R\frac{{n_k^\alpha }}{{\mathop {\sum}\limits_{i = 1}^K n_i^\alpha }}{\kern 1pt} \frac{1}{{n_k^\beta }}.$$
(2)

Here the parameter β is an exponent that represents inefficiency in the distributing process of the group's gain. One can also associate β with a tax rate imposed by a social planner. If β = 1, then there is no negative size effect and the group's gain is fully transferred to its members. On the contrary, for a larger value of β, the members have to take inevitable loss in distribution. As seen in (1) and (2), the group share gk monotonically increases with the group size nk, while the individual payoff πk does not necessarily increases due to the counteracting effects of α and β. Taking these into account, the players seek to form groups that maximize their payoffs.

Sequential maximin group formation

In real-world group formation in large population, avoiding risk would be a major variable in decision-making. We assume that people pursue a secure strategy that ensures their share at a level. This is the maximin strategy and leads people to sequentially form groups. At first, a group of people seek to form a coalition that maximizes the payoff for each member under the presumption that all the other people may form groups which cause the greatest harm to their group. Once their group is formed, those people in the group are locked in, i.e., they do not attract new members or resolve the group whatsoever. Next, the second group is formed among the remaining people in the same manner, taking the formation of the first group as given. This is continued until there is no remaining members.Footnote 3

Let us define the above process of group formation more precisely. Let S(n1,…,nk,*) denote a set of all possible group structures that contain the formerly established k groups with group sizes n1,…,nk, respectively. For example, if the total number of players N is 6, S (2,1,*) is a set of all possible group structures which contain group 1 with its size 2 and group 2 with its size 1:

$$S\left( {2,1,^\ast } \right) = \left\{ {\left( {2,1,3} \right),\left( {2,1,2,1} \right),\left( {2,1,1,2} \right),\left( {2,1,1,1,1} \right)} \right\}.$$
(3)

Now we are ready to consider the players' sequential group formation. If n persons try to make a first group, they prepare for the worst case that the remaining N = n people form group(s) against their group. So, their expectation for the individual gain is pn = minG∈S(n,*)π1(G). The number of the first group, n, will be determined at which pn is maximized. In other words,

$$n_1 = arg\mathop {{max}}\limits_n \mathop {{min}}\limits_{G \in S\left( {n,^\ast } \right)} \pi _1\left( G \right)$$
(4)

Those, who do not form group yet, assume that the members of the established group(s) stick to their "safe" maximin profits and will not be resolved. The second group of people therefore try to maximize their expectation for the possible worst profit \(\mathop {{min}}\nolimits_{G \in S\left( {n_1,n,^\ast } \right)} \pi _2\left( G \right)\) with fixed n1. Hence the group size n2 is determined as

$$n_2 = arg\mathop {{max}}\limits_n \mathop {{min}}\limits_{G \in S\left( {n_1,n,^\ast } \right)} \pi _2\left( G \right)$$
(5)

This process continues until there is no remaining players or the last player is only left. We say that the group structure resulting form this sequential process equipped with the maximin strategy of the players "sequential maximin equilibrium".

Definition(Sequential maximin equilibrium) A group structure G = (n1,…,nk) is said to be a if

$$n_k = arg\mathop {{max}}\limits_n \mathop {{min}}\limits_{G \in S\left( {n_1, \cdots ,n_{k - 1},n,^\ast } \right)} \pi _k\left( G \right),\;{\kern 1pt} k = 1,2, \cdots ,K,$$
(6)

where we set n0 = 0 for consistency of the notation.

It is easily confirmed that a group distribution at sequential maximin equilibrium always exists for any payoff function πk. This is a striking difference in that strong Nash or coalition-proof Nash equilibria rarely exist, or hard to find even when they exist. In the next section, sequential maximin equilibria are evaluated with various values of parameters for as many as 1000 people.

Group formation under various size effects

In order to deal with group formation under the size effects, we now investigate a group distribution at a sequential maximin equilibrium with respect to the payoff (2). In the simple case of α =β = 1, there are no size effects and the payoff becomes a constant πk (G) = R/N for any group distribution G. This implies that all possible group distributions are equally attractive and people are indifferent between staying alone and forming any group. If α is lager than 1, there appears a unique group distribution for each value of α. Especially, if there is only the small positive size effect (α → 1+, β = 1), then people forms two groups of which size ratio is 78:22. (For more detail, refer to Supplement.)

Suppose the inefficiency of within-group distribution dominates. This means that the negative size effect is much larger than the positive one, or, α ≪ β. In this case, people may have no merit in forming groups and determine to remain as singletons.

Group formation begins to appear when the two size effects are competing and almost cancelling each other. For example, let α = 1.4 and β = 1.5 for N = 10. Then a group distribution at a sequential maximin equilibrium is (4, 1, 1, 1, 1, 1, 1). That is, once four persons make a group first, the remaining six decide to stay as singletons. Setting α = β = 1.5 makes people feel more attractive to forming groups and results in a group distribution (5, 2, 1, 1, 1). If we further raise α to 1.6, they end up with three groups, as (5, 3, 2).

As α increases further, the group-size effect starts to outweigh the inefficiency of within-group distribution, driving individuals to prefer larger groups. When the effectiveness of the group size in the contest grows extremely large, the contest becomes like an auction in which the largest group takes all the resource as long as it outnumbers other groups at least by one. This implies that the largest one does not necessarily keep growing and eventually converges to m + 1 as α → ∞, where N = 2m or N = 2m + 1.

We assume α, β > 1 from here on, for more practical size-dependent group formation. From the nature of the negative size effect based on within-group management, a social planner’s controlling β over whole groups may not be feasible. We, therefore, assume that the social planner mostly intervenes at the positive size effect for a given range of β. Since it is not straightforward to derive how the size effects diversifies the group distribution in a general way, we verify the following three special cases of small, middle, and large values of α.

Theorem 1 Suppose β > 1. The group distribution is as follows according to the values of α and β.

  1. a.

    If α < β/2 then G = (1, 1,…,1) i.e., \(\overline G = \left( {\frac{1}{N},\frac{1}{N}, \cdots ,\frac{1}{N}} \right)\).

  2. b.

    If α = β then \(\overline G = \left( {\frac{1}{2},\frac{1}{4},\frac{1}{8}, \cdots } \right)\).

  3. c.

    As α → ∞, \(\overline G \to \left( {\left( {\frac{1}{2}} \right)^ + ,\left( {\frac{1}{2}} \right)^ - } \right)\).

In Fig. 1, the size of the largest group is graphed according the various values of α. The example fixes the negative size effect at β = 2 for the population N = 1000. Figure 1(a) depicts the change of the largest group when α grows toward β = 2. People do not form any group until α gets close enough to β. At a value around 1.87, the first group suddenly appears. Its size increases with α, but the increasing tendency changes from consecutive emergences of the second and third groups. Figure 2(a) extends the graph in a log scale to show convergence of the group size in the limit. As stated in Theorem 1, the group size converges to the half of the population as α → ∞, maintaining largest portion of the population all the way.

Fig. 1
figure 1

Size of the largest group according to the values of α: The population and the negative size effects are set as N = 1000, β = 2. a 1.86 ≤ α ≤ 2; b 1 ≤ α ≤ 100 (log scale)

Full size image
Fig. 2
figure 2

The Pareto ratio and the top-to-bottom ratio according to the positive group effect α: The negative effect is fixed at β = 2

Full size image

Inequalities at group and individual levels

While a variety of group distributions appear according to the size effects, it is notable that they do not directly reflect proportion of the individual payoffs between the groups. In the previous example of β = 1 in which the normalized group distribution approaches to (0.78, 0.22) as α → 1+, the corresponding payoffs π1 and π2 converge to the same value. Similarly, the group distribution (0.5, 0.25, 0.125,…) from α = β > 1 leads to a equal individual payoff in all groups regardless of size. On the contrary, if α is much greater than β, the population breaks into two of the almost same size but a slightly bigger group occupies the most resource. This implies that a member in one group gets almost double of what he/she deserves if it were under mild size effects, while a member in the other group gets nothing.

Our major concern in this work is to investigate the influence of the group size effects on social inequalities in terms of resource allocations among groups and individuals. In order to do this, we formulate two indices that measure social inequalities in our model at group and individual levels, respectively: the Pareto ratio and the top-to-bottom ratio.

Pareto noted that approximately 80% of Italy's wealth is owned by only 20% of the population and many social and physical phenomena have empirically exhibited such ratios as well. In the context of our model, the Pareto principle holds if a group's gain is \(\overline g _k = 0.8\) while its proportion in the population is \(\overline n _k = 0.2\). In this light, we define a Pareto ratio as

$$r_P = \mathop {{max}}\limits_k \frac{{\overline g _k}}{{\overline n _k}}{\kern 1pt} \, \in \left[ {1,N} \right]$$
(7)

to measure how unevenly resource is occupied by groups. If rP ≥ 4 for a group distribution, then the Pareto principle holds and inequality in resource allocation is severe at group level.

It is notable that what a group earns may differ from what the members earn. Even if a group takes a large portion of the resource, due to the within-group distributional inefficiency, the members in that group may get less than members in the other groups. Such ironic situation is not properly captured by the Pareto ratio. Therefore introducing a top-to-bottom ratio

$$r_T = \mathop {{max}}\limits_{i,j} \frac{{\pi _i}}{{\pi _j}}{\kern 1pt} \, \in \left[ {1,\infty } \right)$$
(8)

is reasonable to measure inequality at individual level. Here rT means the ratio between the highest earner and the lowest earner. If rT = 1, then everyone is equal in resource allocation regardless of groups that they belong to. If rT = ∞, then there is an individual who receives nothing at all.

Once again, we consider the situation that the social planner adjusts the positive size effect α for the given negative size effect β > 1. The following is confirmed for the values of two inequality indices rP and rT for the cases dealt in Theorem 1.

Theorem 2 Suppose β > 1. The inequality indices are as follows according to the values of α and β.

  1. a.

    If α < β/2 then rP = rT = 1.

  2. b.

    If α = β then rP = 2−21-α and rT = 1.

  3. c.

    As α → ∞, rP → 2 and rT → ∞.

One can see in Theorems 2 (a) and (c) two extreme cases with large size effects. For excessively large negative size effect as in (a), no one tries to form a group and people remain as homogeneous singletons, resulting in both rP and rT at the minimum value 1. On the contrary, if the positive size effect grows large, then the winner-takes-all situation starts to occur. A group slightly larger than 50% of the population takes almost entire resource, making the Pareto ratio close to 2. Simultaneously the members in the other groups get almost nothing, which implies an extremely large top-to-bottom ratio.

If α happens to be exactly the same as β, the individual inequality is minimized and the Pareto ratio is kept at a decent value near 2. It was noted in the previous section that a variety of group distributions can appear with two size effects closely competing. This implies that the inequality indices also sensitively react to the change of the size effects around α≈β. Figure 2 shows the graphs of rP and rT with respect to α, for β fixed at 2. If α is less than β, there is commonly a mixture of groups and singletons. While most people mind inefficiency of within-group distribution and insist on staying alone, some people start to get together. Note that the grouper's individual payoff may not be large, or may be even smaller than that of singletons due to the negative size effect. The first emergent group is not usually big, but without rival groups, the group's gain overwhelms other singletons' by far. This results in a high Pareto ratio. In Fig. 2, the Pareto ratio rP leaps as high as 12 where α is at around 1.88. This inequality at a group level gradually disappears as α gets closer to β, since other groups are born one by one and start to compete in size.

If α is raised further beyond β, the social inequality reappears again, but at a different level. In this case, no matter how much the members lose from inefficient within-group distribution, their ultimate share depends on the external situation, the whole group distribution. The gap between groups tends to grow rapidly with α. If a group does not maintain competitiveness in relative size, it eventually fails to gain as much resource as its members can share. This produces extremely poor individuals, leading the top-to-bottom ratio rT high.

Slight deviation from the balance α = β may result in social inequality either at group level or individual level. If the negative size effect dominates over the positive one, there is a possibility that the Pareto distribution occurs. On the other hand, if the positive size effect exceeds the negative one, we may have the large rich-poor gap. All in all, one should maintain α≈β in a relatively narrow region as illustrated in Fig. 2, to keep the values of rP and rT reasonably small and achieve social equalities at both group and individual levels.

The social planner may control resource allocation by intervening the both positive and negative group size effects. Cutting down a size-based tax imposed on groups reduces β and increases the mean individual payoff, but it may lead to an ironic situation that the rich-poor gap is much widened. In general, the positive size effect α is more manageable factor in social planning. The effect can be reduced by setting a limit to the maximum resource that can be taken by a single group or by implementing regulations to support relatively small groups. However, suppressing α overly may incubate only a few small coalitions which monopolize most of the resource and create a 80/20 situation.

Discussion

In this work, the individual payoff is designed to reflect the positive and negative size effect to investigate how people form groups and compete for the resource under the group-size effects. We assume that groups are sequentially created by people seeking a conservative strategy to reduce their possible maximum loss. It turned out that the various group distributions occur depending on the size effects.

We are especially interested in a relation between social inequalities in resource distribution and the size effects in group formation. If the size effect that influences on the inter-group competition is too high, it results in severe individual inequality. On the contrary, if individuals in a large group fail to sufficiently receive what their group earns due to inefficient management, it ironically leads to unequal distribution at group level. Since these two size effects counteract and cancel each other in a range, the social planner should keep them in balance by limiting larger one properly. Referring the two inequality indices, the social planner can choose either to support small groups in a contest, or to reduce the progressive tax imposed on each group.

Here we assumed that the resource R is fixed in a contest and not influenced by the group size. However, especially for natural resources, the total exploitable amount may be multiplied by collective work of the population as well. The future study will extend the current work to cases where group distribution also affects production of resources. In addition, the sequential maximin group formation that is proposed as large-group dynamics in this work can be applied to group-related problems created by various social and economic interactions, once it is combined with the corresponding payoff functions.