RETRACTED ARTICLE: Optimal scheduling of integrated energy system based on improved grey wolf optimization algorithm

Abstract

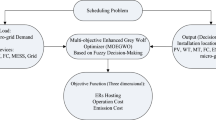
The optimal scheduling problem of integrated energy system (IES) has the characteristics of high-dimensional nonlinearity. Using the traditional Grey Wolf Optimizer (GWO) to solve the problem, it is easy to fall into a local optimum in the process of optimization, resulting in a low-quality scheduling scheme. Aiming at the dispatchability of electric and heat loads, this paper proposes an electric and heat comprehensive demand response model considering the participation of dispatchers. On the basis of incentive demand response, the group aggregation model of electrical load is constructed, and the electric load response model is constructed with the goal of minimizing the deviation between the dispatch signal and the load group aggregation characteristic model. Then, a heat load scheduling model is constructed according to the ambiguity of the human body's perception of temperature. On the basis of traditional GWO, the Fuzzy C-means (FCM) clustering algorithm is used to group wolves, which increases the diversity of the population, uses the Harris Hawk Optimizer (HHO) to design the prey to search for the best escape position, and reduces the local The optimal probability, and the use of Particle Swarm Optimizer (PSO) and Bat Optimizer (BO) to design the moving modes of different positions, increase the ability to find the global optimum, so as to obtain an Improved Gray Wolf Optimizer (IGWO), and then efficiently solve the model. IGWO can improve the defect of insufficient population diversity in the later stage of evolution, so that the population diversity can be better maintained during the entire evolution process. While taking into account the speed of optimization, it improves the algorithm's ability to jump out of the local optimum and realizes continuous deep search. Compared with the traditional intelligent Optimizer, IGWO has obvious improvement and achieved better results. At the same time, the comprehensive demand response that considers the dispatcher's desired signal improves the accommodation of new energy and reduces the operating cost of the system, and promotes the benign interaction between the source and the load.

Introduction

The development of clean, economical and efficient energy supply methods is the focus of the energy sector^1,2,3. IES is an integrated energy system that realizes the production, supply and distribution of energy by giving full play to the complementary characteristics of different energy sources and organically coordinating and optimizing the generation, transmission and distribution, conversion, storage and consumption of energy, and then coupling and transforming multiple types of heterogeneous energy streams to achieve a graded utilization and rational distribution of energy^4,5. As the number of wind power, solar power and other distributed power sources on the grid continues to increase, their greater randomness of power output will pose a threat to the stable operation of the power grid, causing the problem of renewable energy is difficult to accommodate⁶. The participation of demand response can bring the customer side into the scope of power system regulation, which has an important role in improving the load curve and optimal scheduling of the power system⁷. With the continuous development of IES, the traditional power demand response is also gradually developed into integrated demand response^8,9. Compared with the traditional power demand response which is simply time transfer and energy use reduction in the horizontal direction, the integrated demand response updates the response behavior as a combination of energy use type conversion (vertical) and time transfer (horizontal).

The IES of the park is composed of multiple systems coupled with electricity, gas and heat, and the addition of energy hubs and energy coupling equipment diversifies the input and output forms of the system, and based on smart grid technology, it is effective in improving the energy utilization rate and new energy consumption in the park, and has received extensive attention from scholars at home and abroad in recent years. Current domestic and international research on IES in parks is focused on system modeling, simulation analysis, security as well as flexibility, and operational optimization and control¹⁰. Zeng et al.¹¹ starts from the modeling of the IES of the park, takes into account the effects of wind and solar power generation and electric and thermal coupling equipment such as electric boilers, and performs an optimal scheduling analysis with the objective function of minimizing the total cost of operation of the IES of the park. Energy coupling facilities considering electric-thermal systems have a significant role in achieving the accommodation of renewable energy sources such as wind and solar energy and in improving the efficiency of energy use¹². Li et al.¹³ analyzes an IES for a park of the combined cooling-heat-electricity supply type, optimally models a system containing a cooling storage facility, electric and thermal energy storage, and various energy conversion facilities, analyzes the economics of the system considering different energy storage participation and gives a profitability strategy. Zhang et al.¹⁴ mainly discusses the evaluation methods of regional IES in terms of the economy, stability, energy consumption level and environmental protection of the system operation, respectively. Zhou et al.¹⁵ constructed a basic model of a regional IES, established a multi-objective function model with total annual operating costs, pollutant emission costs, and energy consumption costs, and solved the objective function by a two-stage optimization method to propose an operating strategy that maximizes the comprehensive benefits of the system. In the¹⁶, a regional IES model of combined cooling-thermal-electricity supply was established, while the energy storage system was put into the system to break the coupling constraint between the electricity-thermal system, and by coordinating the reasonable output of the energy conversion equipment and the energy storage system in the system, the comprehensive cost of system operation under different operation modes was obtained to verify the advantages of the model in improving the flexibility of system operation as well as the large-scale accommodation of renewable energy such as wind and solar energy. The above literature mainly studies the introduction of electric-thermal coupling facilities and energy storage devices in IES to break the coupling constraint between electric-thermal systems and to verify the effectiveness in improving the output of new energy sources such as wind and solar, mostly by constructing the objective function with the optimal system economy for optimal dispatch. In order to decouple the strong coupling constraint between electric and thermal systems, it is often necessary to increase the investment in the system to improve the operating characteristics of the units, while the feed-in space of wind and solar energy output and the efficiency of energy utilization also need to be further improved.

Among them, the micro gas turbine as the representative of the cogeneration system with high energy step utilization, flexible operation¹⁷, etc., to achieve the scenery and other renewable energy consumption provides an effective way, and minimize the system operating costs, while the introduction of demand-side response can improve the utilization of new energy to a greater extent, reduce pollutant gas emissions to achieve energy saving and emission reduction will be an important development direction of IES^18–19. For this reason, the State Grid proposes to change the role of the traditional electricity supplier to that of a comprehensive energy service provider²⁰. In order to make full use of energy to achieve the economy of IES, researchers in China and abroad have conducted a lot of research around the optimization of IES inter-energy coordination. Dong et al.²¹ proposes to view demand response as standby capacity on the demand side and reserve generation unit standby capacity on the generation side to construct a two-way standby capacity model that facilitates the accommodation of wind energy. Wang et al.²² introduced the basic concept and application value of integrated demand response, summarized the application of integrated demand response in multi-energy systems, and reviewed the existing integrated demand response projects at home and abroad. In the²³, an IES optimal dispatching model considering the participation of the power user side is proposed, which takes into account that the power load has time-shifting characteristics to involve the controllable load in the optimal dispatching of the system. In the²⁴, an integrated demand response for electricity and heat based on the integrated and complementary use of multiple energy sources in the system is proposed, and the optimization strategy of the system is derived with the peaking command of the higher-level grid as the optimization objective. Xuejun et al.²⁵ considers the variability of different customer loads in response to tariffs, and in order to be able to fully demonstrate the different load response capabilities, a coordinated control model for many different load types is developed. Li et al.^26,27,28 fully considers the goal of economic dispatch by using the combined effect of demand response of multi-energy complementarity and peak-shaving and valley-filling of multiple energy storage in the case of multi-energy supply. In the^29,30, the impact of levelizable loads in reducing the integrated operating costs is analyzed, taking into account the levelizable characteristics of the electrical loads and using the combined cooling, heating and power system as an optimization object. There is some literature that focuses the study of IES optimization mainly on the study of thermal systems. Marnay et al.³¹ presents a method for optimizing the operation of micro-energy networks in commercial buildings, showing that collaborative optimization of electric and thermal systems can improve the operational economy of micro-energy networks. In the³², a day-ahead optimal scheduling model for wind-photovoltaic-photothermal co-generation system with price-based demand response is constructed, and the good effect of the model in reducing the integrated cost and improving the scenery consumption capacity is demonstrated by arithmetic examples. Chen et al.³³ established an optimization model for various energy supply methods including CHP, wind energy, electric boilers and thermal storage, and verified the effect of introducing electric boilers and thermal storage devices to improve the flexibility of CHP and effectively reduce the amount of abandoned wind power. Li et al.³⁴ utilizes the heat storage capacity of district heating networks to coordinate the short-term operation of power and district heating systems, effectively promoting wind power access to the grid and facilitating optimal system operation. In the^35,36, the heat transfer characteristics of the heat supply network were modeled to obtain the optimal scheduling strategy for the relationship between the cooling-heat-electricity cogeneration system and the heat supply network, as well as the heat hysteresis and heat loss during the transmission of heat energy in the network.

The optimal scheduling problem of IES has the characteristics of high-dimensional nonlinearity. Traditional mathematical optimization algorithms are no longer suitable for solving such complex problems, and intelligent algorithms are used to solve them. The traditional GWO cannot well balance the global and local optimization capabilities of the algorithm, and cannot achieve continuous speed search³⁷. Zhang et al.³⁸ introduced the elite opposition-learning strategy and simplex method into GWO, proposed a novel hybrid GWO based on elite anti-learning (EOGWO), and tested EOGWO with 13 benchmark functions, and the results showed that, the optimization accuracy, convergence speed and robustness of EOGWO are better than those of the comparison algorithms; Zhu et al.³⁹ integrated the differential evolution algorithm (DEA) into GWO to update the previous best position of gray wolf $\alpha$, $\beta$ and $\gamma$, so as to use the powerful search ability of DEA to make GWO jump out of the local optimum, and the experiments showed that , the convergence speed and performance of the GWO algorithm combined with DEA have been improved; Elgayyar et al.⁴⁰ proposed a hybrid grey wolf-bat optimizer (HGB), in which GWO is used to explore the search space individually and pass the best two solutions to HGB to guide its local Search, then HGB digs deep and finds the best solution.

To sum up, researchers have different findings on the defects of GWO, and the improvement measures taken are also inconsistent. However, the performance of GWO processed by the improvement strategy has been greatly improved, and the improved GWO is used to solve practical engineering problems. Therefore, GWO has a good application prospect and research value.

To sum up, in terms of optimal scheduling of IES, the above-mentioned literatures mainly study the impact on the optimal scheduling results in the IES considering the participation of a single demand response, and verify that the accommodation level of new energy can be improved by considering the participation of demand response. However, with the diversified development of the energy system, the traditional single response form has gradually developed into an electric-heat integrated demand response, and there are few studies on the electric-heat integrated demand response, which is an important development direction for the application of demand-side response technology to an IES in the future. In terms of solving the optimal dispatching problem of integrated energy system, the above literature shows that the solution based on traditional GWO will make the final solution of the dispatching scheme of low quality. Therefore, the research of existing literature mainly focuses on the improvement of traditional GWO, so that the improved GWO has better performance, and then solves the problem efficiently.

This paper proposes a comprehensive electric-thermal demand response model considering load-following dispatch signals with the participation of dispatchers, and proposes an IGWO to solve this problem efficiently. Compared with the existing research, the innovations and contributions of this paper are as follows:

• (1) In this paper, an electrical load scheduling model considering the participation of dispatchers' expected signals and a heat load scheduling model with ambiguity in the human body's perception of temperature are established.

• (2) The level of new energy accommodation can be improved with the integrated demand response of electricity and heat considering the expectation signal of dispatchers.

• (3) This paper realizes the economic operation of the IES through the dynamic modeling of source-grid-load-storage and the optimization of the objective function.

• (4) In this paper, an IGWO is proposed to efficiently solve the optimal scheduling problem of IES, which not only obtains a high-quality scheduling scheme, but also has a strong global search ability.

Integrated demand response model for electric and thermal multiple loads

Schedulability analysis of electric and thermal load demand response

Traditional demand-side response only considers the economics of a single energy network, and customers will consider their own interests to adjust their electricity consumption arrangements and thus participate in the system dispatch⁴¹. As IES research continues, the traditional response approach is no longer sufficient for the application of IES in new forms. The continuous strengthening of the coupling of heat and power requires that not only the balance of supply and demand for electricity but also for heat be met. Therefore, the power demand-side response in this paper will be studied from the IES as a whole. TSL is defined as Time-shift Load (TSL), which has good flexibility in the time of electricity consumption and can be adjusted according to the economic optimization target of the system, so that the electricity consumption in each time period can be changed and thus affect the energy supply side to achieve the purpose of overall system optimization.

In IES, thermal loads are at the end of energy consumption like electric loads, so thermal loads can also be exploited for their unique scheduling value. The thermal load is optimized according to the ambiguity of temperature perception of thermal users. In China's design specifications, it is appropriate to have a mean scale prediction (PMV) index of thermal sensation between ± 1, i.e. the heat supplied by the heat supply side is allowed to fluctuate within a certain range. Thus the thermal load can be involved in the demand-side response of the whole system as a flexible load.

Power load demand response modeling

The demand characteristics of TSL can be shifted left and right on the time axis, and $D\left( {t - \tau_{2} } \right)$ and $D\left( {t + \tau_{1} } \right)$ denote the demand characteristics with lag $\tau_{2}$ and time ahead of $\tau_{1}$. Its group aggregation characteristics can be expressed by the following equation:

$$g\left( {m_{i,j} ,n_{i,k} ,\tau 1_{i,j} ,\tau 2_{i,k} ,t} \right) = \sum\limits_{i = 0}^{NT} {\left( {\begin{array}{*{20}c} {\sum\limits_{j = 0}^{\infty } {\left( {m_{i,j} \cdot D_{i} \left( {t + \tau 1_{i,j} } \right)} \right)} } \\ {\quad + \sum\limits_{k = 0}^{\infty } {\left( {n_{i,k} \cdot D_{i} \left( {t - \tau 2_{i,k} } \right)} \right)} } \\ \end{array} } \right)}$$

(1)

where: j and k are the time possible situation limits for time shifts within the TSL overrun and lag time limits; the upper bounds of j and k indicate that there are infinitely many possible time shifts of TSL within the overrun time limit and lag time limit, respectively, and the lower bounds indicate no shifts; NT is the type of participating scheduling; $D_{i} \left( {t + \tau 1_{i,j} } \right)$, $D_{i} \left( {t - \tau 2_{i,k} } \right)$ are the class i TSL overrun $\tau 1_{i,j}$ and lagging $\tau 2_{i,k}$; $m_{i,j}$, $n_{i,k}$ are the number of class i TSLs overtaking $\tau 1_{i,j}$ and lagging $\tau 2_{i,k}$. Since this paper considers day-ahead optimal scheduling, we can let $\tau 1_{i,j}$ and $\tau 2_{i,k}$ be 1 h, then the maximum overrun as well as lag time can be expressed as:

$$\begin{aligned} \max 1\left( i \right) & = ST_{i} \\ \max 2\left( i \right) & = T - ED_{i} \\ \end{aligned}$$

(2)

In order to level out the output of each unit in the system, the desired signal is introduced into the model to define the objective function as the minimum deviation of the TSL aggregation characteristic from the desired signal, i.e.

$$X = \int_{0}^{T} {\left[ {\begin{array}{*{20}c} {x\left( t \right) - } \\ {g\left( {m_{i,j} ,n_{i,k} ,\tau 1_{i,j} ,\tau 2_{i,k} ,t} \right)} \\ \end{array} } \right]^{2} dt}$$

(3)

where: $X$ is the magnitude of the deviation value after dispatching; $x\left( t \right)$ is the dispatching signal.

In the above equation, the expected signal of the dispatcher is the demand value under the expectation of each different time period predicted from the previous day's load, and the deviation value of the group aggregation characteristic from the dispatch signal is expressed as a square, so that the electric load can track the expected signal of the dispatcher to the maximum extent based on the incentive response, so that the system can flatten the unit output curve while coping with the volatility and uncertainty of wind and solar power output and load.

The constraints of the model can be expressed as follows:

• (1) The sum of the total TSL time-shiftable load is equal to the total number of participating users, i.e.

  $$\sum\limits_{j = 0}^{\max 1\left( i \right)} {m_{i,j} } + \sum\limits_{k = 0}^{\max 2\left( i \right)} {n_{j,k} } = \sum\limits_{i = 1}^{NT} {N_{i} }$$

  (4)

  where: $N_{i}$ is the amount of users involved in TSL of type i.

• (2) Overrun and lag time constraints

  $$\begin{aligned} & 0 \le \tau 1_{i,j} \le ST_{i} \\ & 0 \le \tau 2_{i,k} \le T - ED_{i} \\ \end{aligned}$$

  (5)

  where: $ST_{i}$, $ED_{i}$ are the start working time and end time under the normal demand of the class i load, and the TSL is guaranteed by the constraint that it cannot start working before to the previous day and end working on the same day.

• (3) Group time-shift electrical energy conservation constraint

  $$\begin{aligned} E_{n} & = \int_{0}^{T} {g\left( {m_{i,j} ,n_{i,k} ,\tau 1_{i,j} ,\tau 2_{i,k} ,t} \right)dt} \\ & = \sum\limits_{t = 1}^{NT} {\left( {\begin{array}{*{20}c} {\sum\limits_{j = 0}^{\max 1(i)} {\left( {m_{i,j} \cdot \int_{0}^{T} {D_{i} \left( {t + \tau 1_{i,j} } \right)} dt} \right)} } \\ {\quad + \sum\limits_{k = 0}^{\max 2(i)} {\left( {n_{i,k} \cdot \int_{0}^{T} {D_{i} \left( {t - \tau 2_{i,k} } \right)} dt} \right)} } \\ \end{array} } \right)} \\ & = \sum\limits_{i = 1}^{NT} {\left( {E_{i} \cdot N_{i} } \right)} \\ \end{aligned}$$

  (6)
  $$E_{n} = \int_{0}^{T} {x\left( t \right)dt}$$

  (7)

  where: $E_{n}$ and $E_{i}$ are the power demand of the aggregated characteristics of the load group and the power demand of the TSL unit of class i.

Thermal load demand response modeling

The user's perception of the heating temperature is ambiguous, so the size of the heat supply can be adjusted within a certain range. On the other hand, heat energy has thermal inertia in transmission, based on which the thermal load can participate in the demand-side response as a flexible load. The specific heat capacity of water in the heat transfer process is c. The heat supplied by the heating equipment at time t is $H_{HS} \left( t \right)$, and the water passing through the heat source mass $Q_{HS}$ rises from the return temperature $T_{h} \left( t \right)$ to the supply temperature $T_{g} \left( t \right)$, then we have^35,36:

$$H_{HS} \left( t \right) = c \cdot Q_{HS} \left( {T_{{\text{g}}} \left( t \right) - T_{h} \left( t \right)} \right)$$

(8)

The heat consumed by the load node in time period t is $H_{L} \left( t \right)$, then by the heat load mass of $Q_{L}$ water from the supply temperature $T_{{\text{g}}} \left( t \right)$ down to the return temperature $T_{h} \left( t \right)$, then we have^35,36:

$$H_{L} \left( t \right) = c \cdot Q_{L} \left( {T_{{\text{g}}} \left( t \right) - T_{h} \left( t \right)} \right)$$

(9)

Considering the need to meet the user's comfort level with respect to temperature, the heat absorbed by the load node at time t, $H_{L} \left( t \right)$, should be within a certain range, i.e.

$$H_{L}^{\min } \left( t \right) \le H_{L} \left( t \right) \le H_{L}^{\max } \left( t \right)$$

(10)

It is also necessary to ensure that the size of the total heat consumed by the heat load in the time period $T^{\prime}$ is the same as the size of the total heat demand of the ideal type of the user^35,36, i.e.

$$\sum\limits_{t = n}^{{n + T^{\prime}}} {H_{L} \left( t \right)} = \sum\limits_{t = n}^{{n + T^{\prime}}} {H_{L}^{ideal} } \left( t \right)$$

(11)

$$T^{\prime} = m \cdot \, \Delta t$$

(12)

where: $T^{\prime}$ is the maximum number of consecutive dispatching periods in the dispatching cycle.

The supply water temperature as well as the return water temperature are constrained to be:

$$T_{g}^{\min } \left( t \right) \le T_{g} \left( t \right) \le T_{g}^{\max } \left( t \right)$$

(13)

$$T_{h}^{\min } \left( t \right) \le T_{h} \left( t \right) \le T_{h}^{\max } \left( t \right)$$

(14)

where: $T_{h}^{\min }$ and $T_{h}^{\max }$ are the maximum and minimum values of return water temperature; $T_{g}^{\min }$ and $T_{g}^{\max }$ are the maximum and minimum values of water supply temperature.

Methods: electricity and heat integrated demand response IES optimization scheduling model

IES structural components

The IES studied in this paper mainly consists of wind energy (WT), solar energy (PV), gas turbine (MT), electric heat boiler (EB), gas boiler (BL), energy storage battery (EES), heat storage tank (HS), and demand-side electric heat load. The overall structure is shown in Fig. 1.

Figure 1

Regional type IES map.

Among other things, the power system can operate in parallel or in isolation from the larger grid and trade tariffs with the grid. Gas turbine cogeneration units (CHP) can generate electricity and heat while consuming natural gas, and there are electric boilers for electric heat production, and their presence makes the electricity-gas-heat triad more closely coupled. By adjusting the power output of each device, the whole system is operated in an optimal state.

Modeling of each device of the IES

• (1) Renewable generations models

Studies have shown that Wind Turbine output power $P_{WT}$ depends on the wind speed and the rated output power $P_{r}$ of Wind Turbine⁴². In addition, the wind speed follows a Weibull distribution. Therefore, the probability density function (PDF) of $P_{WT}$ can be expressed as⁴³:

$$f_{w} \left( {P_{WT} } \right) = \left\{ {\begin{array}{*{20}l} {\left( {khv_{in} /\varepsilon P_{r} } \right)} \hfill \\ {\; \times \left[ {\left( {\left( {1 + hP_{WT} /P_{r} } \right)v_{in} } \right)/\varepsilon } \right]^{k - 1} } \hfill \\ {\; \times \exp \left\{ { - \left[ {\left( {\left( {1 + hP_{WT} /P_{r} } \right)v_{in} } \right)/\varepsilon } \right]^{k} } \right\}} \hfill \\ {P_{WT} \in \left[ {0,P_{r} } \right]} \hfill \\ {0,\;{\text{otherwise}}} \hfill \\ \end{array} ,} \right.$$

(15)

where: $\varepsilon$ and $k$ are the scale factor and shape factor, respectively, taken as 1.8 and 10, respectively;$h = \left( {v_{r} /v_{in} } \right) - 1$; $v_{in}$ and $v_{r}$ are the cut-in wind speed and the rated wind speed respectively, which are taken as 3 m/s and 15 m/s respectively. More details on the stochastic model of wind power output can be found in⁴³.

The research shows that the solar irradiance approximately obeys the Beta distribution, and the photovoltaic output power $P_{V}$ has a linear relationship with the solar irradiance^44,45. Therefore, the PDF of $P_{V}$ can be represented as⁴³:

$$f_{p} \left( {P_{V} } \right) = \frac{{\Gamma \left( {\mu_{1} } \right) + \Gamma \left( {\mu_{2} } \right)}}{{\Gamma \left( {\mu_{1} } \right)\Gamma \left( {\mu_{2} } \right)}}\left( {\frac{{P_{V} }}{{P_{V}^{\max } }}} \right)^{{\mu_{1} - 1}} \left( {1 - \frac{{P_{V} }}{{P_{V}^{\max } }}} \right)^{{\mu_{2} - 1}}$$

(16)

where: $P_{V}^{\max }$ is the maximum value of $P_{V}$, which is taken as 198.4 kW; $\mu_{1}$ and $\mu_{2}$ are shape factors, taken as 3 and 5, respectively; $\Gamma$ is a Gramma function.

In order to reduce the influence of uncertainty on system scheduling, this paper adopts the processing method of literature⁴³: the mathematical expectations $P_{WT}$ and $P_{V}$ of $E\left( {P_{WT} } \right)$ and $E\left( {P_{V} } \right)$ in each time period are used as reference values. More details can be found in⁴³.

• (2) CHP model¹²

The electrical and thermal power generated by the cogeneration units consuming natural gas is shown below:

$$P_{MT} \left( t \right) = \frac{{V_{MT} \left( t \right) \cdot \eta_{MT,e} \cdot LHV}}{\Delta t}$$

(17)

$$H_{MT} \left( t \right) = P_{MT} \left( t \right) \cdot \frac{{\left( {1 - \eta_{MT,e} - \eta_{L} } \right)k_{h} }}{{\eta_{MT,e} }}$$

(18)

where: $P_{MT} \left( t \right)$ and $H_{MT} \left( t \right)$ denote the electric power and thermal power emitted by CHP at time t, respectively; $V_{MT} \left( t \right)$ is the consumption of natural gas at time t; LHV is the low heating value of natural gas; $\eta_{MT,e}$, $\eta_{L}$, and $k_{h}$ are the power generation efficiency, heat loss rate, and transmission efficiency of the exchanger, respectively; $\Delta t$ is the unit time period.

• (3) Gas boiler model¹⁶

  $$H_{Bl} \left( t \right) = \eta_{Bl} \cdot Q_{gas} \left( t \right) \cdot LHV$$

  (19)

  where: $H_{Bl} \left( t \right)$ and $Q_{gas} \left( t \right)$ are the thermal power output and the amount of natural gas consumed at moment t; $\eta_{Bl}$ is the boiler combustion efficiency.

• (4) Heat producing electric boiler model¹⁶

  $$H_{eb} \left( t \right) = P_{eb} \left( t \right) \cdot \eta_{eb}$$

  (20)
  $$H_{eb}^{\min } \le H_{eb} \left( t \right) \le H_{eb}^{\max }$$

  (21)

  where: $P_{eb} \left( t \right)$, $H_{eb} \left( t \right)$ are the electrical power consumed and thermal power generated at moment t; $\eta_{eb}$ is the heating efficiency; $H_{eb}^{\min }$, $H_{eb}^{\max }$ are the upper and lower limits of heat production.

• (5) Battery model²⁴

  $$\begin{aligned} Bat_{soc} \left( t \right) & = \left( {1 - \mu } \right)Bat_{soc} \left( {t - 1} \right) \\ & \quad + \left[ {P_{bat}^{in} \left( t \right)\eta_{in} - \frac{{P_{bat}^{out} \left( t \right)}}{{\eta_{out} }}} \right]\Delta t \\ \end{aligned}$$

  (22)

  where: $Bat_{soc} \left( t \right)$ is the power storage at time t; $P_{bat}^{in} \left( t \right)$ and $P_{bat}^{out} \left( t \right)$ are the charging and discharging power at time t; $\mu$, $\eta_{in}$, $\eta_{out}$ are the self-discharge rate and charging and discharging efficiency.

• (6) Heat storage tank model¹⁶

  $$\begin{aligned} Q_{soc} \left( t \right) & = \left( {1 - \tau } \right)Q_{soc} \left( {t - 1} \right) \\ & \quad + \left[ {H_{soc}^{in} \left( t \right) \cdot \eta_{hch} - \frac{{H_{soc}^{out} \left( t \right)}}{{\eta_{hdls} }}} \right]\Delta t \\ \end{aligned}$$

  (23)

  where: $Q_{soc} \left( t \right)$ is the heat storage capacity at time t; $H_{soc}^{in} \left( t \right)$, $H_{soc}^{out} \left( t \right)$ are the heat absorption and discharge power at time t; $\tau$, $\eta_{hch}$, $\eta_{hdls}$ are the heat loss rate as well as the heat absorption and discharge efficiency.

Objective function

The intraday operating cost of an integrated campus energy system consists of three main components: purchased energy, equipment operation, and dispatch response costs. The first part is the cost of burning natural gas in CHP units and gas boilers and the cost of purchasing power from the grid; the second part is the cost of operation and maintenance, start-up and shutdown of each equipment output; and the third part is the cost of responding to TSL tracking and dispatching signals. The integrated demand-side response of electricity and heat is considered, and the power output of each equipment unit is reasonably arranged to minimize the total cost of the whole system operation, and a comprehensive energy system optimization dispatching model with integrated demand response is constructed. The objective function is:

$$\min F = F_{MT} + F_{gas} + F_{grid} + F_{mc} + F_{qt} + F_{TSL}$$

(24)

$$F_{MT} = \sum\limits_{t = 1}^{T} {\left( {C_{{CH_{4} }} \frac{{P_{MT} \left( t \right)}}{{LHV \cdot \eta_{MT,e} }}} \right)\Delta t}$$

(25)

$$F_{gas} = \sum\limits_{t = 1}^{T} {\left( {C_{{CH_{4} }} \cdot Q_{gas} \left( t \right)} \right)} \Delta t$$

(26)

$$F_{grid} = C_{grid} \cdot \sum\limits_{t = 1}^{T} {P_{grid} } \left( t \right)\Delta t$$

(27)

$$F_{mc} = C_{mc} \cdot \sum\limits_{t = 1}^{T} {P_{n} } \left( t \right)\Delta t$$

(28)

$$\left\{ \begin{gathered} U_{n} \left( t \right) = V_{n} \left( {t - 1} \right) \cdot \left( {1 - V_{n} \left( t \right)} \right) \hfill \\ \; + V_{n} \left( t \right) \cdot \left( {1 - V_{n} \left( {t - 1} \right)} \right) \hfill \\ F_{qt} = \sum\limits_{t = 1}^{T} {\left[ {C_{qt,n} \cdot U_{n} \left( t \right)} \right]} \Delta t \hfill \\ \end{gathered} \right.$$

(29)

$$F_{TSL} = \sum\limits_{t = 1}^{T} {\left( {R_{TSL} \cdot X} \right)} \Delta t$$

(30)

where: $F$ is the total cost of system operation; $F_{MT}$ is the cost of natural gas consumed by the CHP unit; $C_{{CH_{4} }}$ is the gas price of natural gas; $P_{MT} \left( t \right)$ is the electric power generated by the unit at moment t; LHV is the low heating value of natural gas; $\eta_{MT,e}$ is the generation efficiency of the unit; $F_{gas}$ is the cost of natural gas consumed by the gas boiler; $Q_{gas} \left( t \right)$ is the amount of natural gas consumed by the gas boiler at moment t. $F_{grid}$ is the cost of interaction with the grid; $C_{grid}$ is the cost coefficient of power purchase; $P_{grid} \left( t \right)$ is the power of system interaction with the grid; $F_{mc}$ is the maintenance cost of each equipment; $C_{mc}$ is the maintenance coefficient cost of each equipment; $P_{n} \left( t \right)$ is the power output of each equipment; $F_{qt}$ is the start-stop cost of the equipment; $C_{qt,n}$ is the start-stop cost of equipment n; $V_{n} \left( t \right)$ is the start-stop state of the equipment, 1 indicates that the unit is in operation and 0 indicates that the unit is in stop state; $F_{TSL}$ is the response cost of TSL following the dispatch signal; $R_{TSL}$ is the incentive response cost coefficient of TSL following the dispatch signal.

Constraints

The simultaneous participation of electric and thermal loads in demand response requires the IES of the park to keep the electric system and thermal system in balance at all times, and to ensure that the input and output of energy are kept in balance at all times. In order to meet the constraints of system operation, in addition to meeting the electrical and thermal power balance constraints, the operating constraints associated with each unit must also be met.

• (1) Power System Balance Constraints⁴⁶

  $$\begin{aligned} & P_{WT} \left( t \right) + P_{V} \left( t \right) + P_{MT} \left( t \right) + P_{grid} \left( t \right) + P_{bat}^{in} \left( t \right) \\ & \quad = P_{bat}^{out} \left( t \right) + P_{load} \left( t \right) + P_{eb} \left( t \right) \\ \end{aligned}$$

  (31)

  where: $P_{load} \left( t \right)$ is the demand for optimal TSL adjustment after the introduction of the desired dispatch signal $x\left( t \right)$ on the electric load side; $P_{WT} \left( t \right)$ and $P_{V} \left( t \right)$ are the output of wind power and PV power in period t, respectively.

• (2) Heating network balance constraint³⁶

  $$H_{eb} \left( t \right) + H_{MT} \left( t \right) + H_{bl} \left( t \right) + H_{soc}^{in} \left( t \right) = H_{soc}^{out} \left( t \right) + H_{load} \left( t \right)$$

  (32)

  where: $H_{load} \left( t \right)$ is the heat user demand after the heat load is involved in demand response optimization adjustment.

• (3) Controllable unit climbing constraint⁴⁶

The output of the unit during operation is to be within the allowable range with the output constraint of:

$$- r_{dl} \Delta t \le P_{MT} \left( t \right) - P_{MT} \left( {t - 1} \right) \le r_{ul} \Delta t$$

(33)

where: $- r_{dl}$, $r_{ul}$ are the rate limits for loading and unloading of controllable CHP units in time period t.

• (4) Interaction power constraints with the larger grid⁴⁷

  $$P_{grid}^{\min } \le P_{grid} \left( t \right) \le P_{grid}^{\max }$$

  (34)

  where: $P_{grid}^{\min }$ and $P_{grid}^{\max }$ are the upper and lower limits of the interactive power with the grid, respectively.

• (5) Energy Storage Battery Constraints²⁴

  $$\left\{ {\begin{array}{*{20}l} {P_{bat}^{\min } \le P_{bat}^{in} \left( t \right) \le P_{bat}^{\max } } \hfill \\ {P_{bat}^{\min } \le P_{bat}^{out} \left( t \right) \le P_{bat}^{\max } } \hfill \\ {Bat_{soc}^{\min } \le Bat_{soc} \left( t \right) \le Bat_{soc}^{\max } } \hfill \\ {P_{bat}^{in} \left( t \right) \cdot P_{bat}^{out} \left( t \right) = 0} \hfill \\ {Bat_{soc} \left( 0 \right) = Bat_{soc} \left( T \right)} \hfill \\ \end{array} } \right.$$

  (35)

  where: $P_{bat}^{\min }$ and $P_{bat}^{\max }$ are the upper and lower limits of electric storage charging and discharging power; $Bat_{soc}^{\min }$ and $Bat_{soc}^{\max }$ are the upper and lower capacity constraints; $Bat_{soc} \left( 0 \right)$ and $Bat_{soc} \left( T \right)$ are the initial and end values of electric storage in the dispatching cycle; and it is also constrained that the electric storage can only operate in one state in a t time period, and it is stipulated that the storage will return to the initial state after one dispatching cycle.

• (6) Heat storage tank constraints¹⁶

  $$\left\{ {\begin{array}{*{20}l} {H_{soc}^{\min } \le H_{soc}^{in} \left( t \right) \le H_{soc}^{\max } } \hfill \\ {H_{soc}^{\min } \le H_{soc}^{out} \left( t \right) \le H_{soc}^{\max } } \hfill \\ {Q_{soc}^{\min } \le Q_{soc} \left( t \right) \le Q_{soc}^{\max } } \hfill \\ {H_{soc}^{in} \left( t \right) \cdot H_{soc}^{out} \left( t \right) = 0} \hfill \\ {Q_{soc} \left( 0 \right) = Q_{soc} \left( T \right)} \hfill \\ \end{array} } \right.$$

  (36)

  where: $H_{soc}^{\min }$ and $H_{soc}^{\max }$ are the upper and lower limits of the heat storage tank charging and discharging power; $Q_{soc}^{\min }$ and $Q_{soc}^{\max }$ are the upper and lower limits of the heat storage capacity constraints; $Q_{soc} \left( 0 \right)$ and $Q_{soc} \left( T \right)$ are the initial and end values of the heat storage tank during the scheduling cycle; and the heat storage tank is also constrained to operate in only one state during a t period, and it is stipulated that the heat storage capacity will return to the initial state after one scheduling cycle.

Methods: solving an integrated demand response IES optimization dispatch model for electricity and heat

The optimal scheduling problem of IES is a nonlinear optimization problem, which has the characteristics of complex constraints and high solution dimensions^48,49,50. In this paper, the IGWO is used to solve the problem. It should be specially pointed out that the parameters set by IGWO in the simulation experiment process can be referred to^51,52,53,54.

GWO is a novel intelligent algorithm, proposed by Mirialili et al. in 2014⁵⁵. The optimization process of the GWO contains the steps of social hierarchy stratification, tracking, encircling and attacking the prey of the gray wolf. Although the regular GWO has better performance than most intelligent algorithms, it is not suitable for handling functions of high complexity. And how to improve the balance between global search and local convergence is one of the important directions to improve the performance of the GWO⁵⁶.

The GWO is similar to the PSO in that it requires a high initial solution set, and the selection of its solution set affects the global search ability and local convergence of the whole algorithm. This algorithm simulates the continuous hunting process of the gray wolf population by Monte Carlo (MC) at the early stage of the search for superiority, and selects the better individuals in the hunting process to form the initial population to ensure the global nature of the population, so as to obtain a reasonable initial solution set.

In addition, the original GWO avoids the algorithm from falling into local optimum by selecting three leading wolves $\alpha$, $\beta$, and $\gamma$. However, when all three leading wolves are locally optimal solutions, the algorithm still has the risk of falling into local optimum. This algorithm groups the initial wolf packs by FCM clustering algorithm, and selects the leading wolf $\alpha$ of each group as the representative of each group by comparing the individual fitness of each group, which increases the diversity of the population and avoids the algorithm falling into local optimum. Equation (37) (displacement update formula of the PSO) is then used to update the position of each group of leader wolves $\alpha$ so that each group of leader wolves $\alpha$ is optimal in a small area around it, avoiding the risk of each group's search result falling into local suboptimality when the search range of individual gray wolves is wide and the leader wolves $\alpha$ is locally suboptimal.

$$\left\{ {\begin{array}{*{20}l} {\Delta w = \frac{{\left( {w_{\max } - w_{\min } } \right)\left[ {f\left( {x_{i}^{d} } \right) - f_{\min }^{d} } \right]}}{{f_{average}^{d} - f_{{\min^{d} }} }}} \hfill \\ {w_{i}^{d} = \left\{ {\begin{array}{*{20}l} {w_{\min } + \Delta w,} \hfill & {f\left( {x_{i}^{d} } \right) \le f_{average}^{d} } \hfill \\ {w_{\max } ,} \hfill & {f\left( {x_{i}^{d} } \right) > f_{average}^{d} } \hfill \\ \end{array} } \right.} \hfill \\ {V_{i}^{k + 1} = w_{i}^{d} V_{i}^{k} + c_{1} rand_{1} \left( {P_{best} - X_{i}^{k} } \right) + } \hfill \\ {{\mkern 1mu} {\mkern 1mu} c_{2} rand_{2} \left( {G_{best} - X_{i}^{k} } \right)} \hfill \\ {X_{i}^{k + 1} = X_{i}^{k} + V_{i}^{k + 1} } \hfill \\ \end{array} } \right.$$

(37)

where: $w_{i}^{d}$ is the inertia weight; $w_{\min }$ and $w_{\max }$ are the preset minimum and maximum inertia coefficients, generally $w_{\min }$ takes 0.4 and $w_{\max }$ takes 0.9; $f_{average}^{d}$ is the average fitness of all particles at the dth iteration; $f_{\min }^{d}$ is the minimum fitness of all particles at the dth iteration; $V_{i}^{k}$ is the velocity and direction of the kth search of the ith particle; $X_{i}^{k}$ is the position of the kth search of the ith particle; $P_{best}$ is the individual optimal solution; $G_{best}$ is the population optimal solution; $c_{1}$ and $c_{2}$ are the ability to make the particle have the ability to self-summarize and learn from the outstanding individuals in the group, which is the learning factor, both of which are taken as 1.5; $rand_{1}$ and $rand_{2}$ are a uniformly distributed random number between 0 and 1.

At the same time, the prey's escape location is continuously updated and the optimal prey escape location is found using MC stochastic simulation using Eq. (38) (detection equation of HHO), which avoids jumping out of the prey's location prematurely when it is locally suboptimal in a small surrounding area, thus reducing the probability of the optimal result being locally optimal.

$$\left\{ {\begin{array}{*{20}l} {\Delta X_{1} = X_{rand} \left( t \right) - 2r_{2} X\left( t \right)} \hfill \\ {\Delta X_{2} = X_{rabbit} \left( t \right) - X_{m} \left( t \right)} \hfill \\ {A = lb + r_{4} (ub - lb)} \hfill \\ {X\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {X_{rand} \left( t \right) - r_{1} \left| { \, \Delta X_{1} } \right|,} \hfill & {q \ge 0.5} \hfill \\ {\Delta X_{2} - r_{3} A,} \hfill & {q < 0.5} \hfill \\ \end{array} } \right.} \hfill \\ {X_{m} \left( t \right) = \sum\limits_{k = 1}^{M} {\frac{{X_{k} \left( t \right)}}{M}} } \hfill \\ \end{array} } \right.$$

(38)

where: $X\left( t \right)$ and $X\left( {t + 1} \right)$ are the positions of individuals at the current and next iterations, respectively; t is the number of iterations; $X_{rand} \left( t \right)$ is the position of a randomly selected individual; $X_{rabbit} \left( t \right)$ is the prey position, i.e., the position of an individual with optimal fitness; $q$、$r_{1}$、$r_{2}$、$r_{3}$ and $r_{4}$ are all random numbers between $\left[ {0,1} \right]$, where $q$ is used to randomly select the strategy to be adopted; $X_{k} \left( t \right)$ is the average position of the individual, that is, the position of the kth individual in the population; $ub$ and $lb$ are the upper and lower bounds of the search space, respectively; $M$ is the population size.

The remaining wolves in each group except the leading wolf $\alpha$ are randomly selected with probability P to choose the pursuer, and their positions are updated by Eq. (39) (displacement update formula of the GWO) to ensure the search ability of the pursuer within the group, and Eq. (37) (velocity update formula of the PSO) is introduced for the secondary update, introducing the current global optimal solution as the reference quantity to improve the pursuer of each group of wolves cooperative hunting ability and reduces the probability of the wolf pack falling into the local optimum. The remaining wolves in each group except the leader $\alpha$ are randomly selected with probability (1 − P) to select the vigilant, and their positions are updated by Eq. (40) (the displacement update formula of the BO), which reduces the probability of prey escape and improves the ability of the algorithm to leap out of the local area.

$$\left\{ {\begin{array}{*{20}l} {D = \left| {C \cdot X_{p} \left( t \right) - X\left( t \right)} \right|} \hfill \\ {X\left( {t + 1} \right) = X_{p} \left( t \right) - A \cdot D} \hfill \\ {A = 2a \cdot r_{1} - a} \hfill \\ {C = 2 \cdot r_{2} } \hfill \\ \end{array} } \right.$$

(39)

where: t is the number of current iterations; $D$ is the distance between the individual and the prey; $A$ and $C$ are coefficient vectors; $X_{p} \left( t \right)$ denotes the position vector of the prey; $X\left( t \right)$ denotes the current position vector of the gray wolf; $a$ decreases linearly from 2 to 0 throughout the iterations; $r_{1}$ and $r_{2}$ are random vectors in $\left[ {0,1} \right]$.

$$\left\{ {\begin{array}{*{20}l} {f_{i} = f_{\min } + \left( {f_{\max } - f_{\min } } \right)\beta } \hfill \\ {v_{i}^{t} = v_{i}^{t - 1} + \left( {x_{i}^{t} - x_{*} } \right)f_{i} } \hfill \\ {x_{i}^{t} = x_{i}^{t - 1} + v_{i}^{t} } \hfill \\ \end{array} } \right.$$

(40)

where: $\beta$ is a random value within $\left[ {0,1} \right]$; $x_{*}$ is the current optimal individual position; $f_{i}$ is the frequency of the sound wave emitted by the bat, and its value is between $\left[ {f_{\min } ,f_{\max } } \right]$, where $f_{\min }$ is 0 and $f_{\max }$ is 2.

Finally, a memory bank is added to save the position and other parameters of each group of wolves during the first $n$ ($n$ is 50) iterations, and the individual with a larger crowding degree is selected as the current individual through the analysis of the crowding degree, which ensures the diversity of each group of populations. It avoids the overcrowding of the wolves, so that the wolves will not fall into the local optimum, and will not lose the search ability at the end of the iteration.

The IGWO applied to the IES scheduling optimization solution steps are shown below:

• Step 1: Set the parameters and data of the IES optimization model;

• Step 2: Set each parameter of the algorithm and initialize the gray wolf population;

• Step 3: Using MC to simulate the continuous hunting process of the gray wolf population, the best position of an individual is selected as the initial position of that individual, thus updating the entire gray wolf population;

• Step 4: Grouping of wolves using the FCM clustering algorithm to prepare wolves for the collaborative hunting process.

• Step 5: Select the leader wolves in each group and update the position of each leader wolf using the displacement update formula in the PSO;

• Step 6: Prey escape location is constantly updated by HHO and MC random simulation is used to find the best prey escape location;

• Step 7: The remaining wolves in each group except the leader are randomly selected with probability P and their positions are updated by the displacement update formula of the GWO and the PSO;

• Step 8: The remaining wolves in each group except the leader are randomly selected with probability (1-P) and their positions are updated by the displacement update formula of the BO;

• Step 9: Add a memory bank to save the parameters such as the position of each group of wolves during the first n iterations, and select the individual with greater crowding degree as the current individual by crowding degree analysis, and save the best individual in the wolf pack;

• Step 10: Determine whether the maximum number of iterations is reached, and if it is satisfied, output the optimal individual, otherwise skip to Step5 until the termination condition is satisfied.

Ethics approval and consent to participate

It is declared that this paper does not involve any human participants, human data or human tissue.

Case studies

In order to increase the feed-in space for system wind and solar power and minimize system operating costs, the traditional single demand response is gradually evolving into an integrated electric-thermal demand response. To verify the role of integrated electricity-thermal demand response in system optimal dispatch, an integrated electricity-thermal demand response optimal dispatch model is constructed for the dispatchable values of electric and thermal loads based on the IES model of the park proposed in “Modeling of each device of the IES” section. And the electric-thermal response is set up for three different cases to verify the role of the introduction of integrated demand response in improving system energy utilization and wind and solar energy accommodation.

Basic data

The IES of a region in northern China in winter was selected for the analysis. The model becomes a mixed-integer quadratic programming problem with the introduction of decision variables, and is solved using the IGWO. The original demand characteristics of the district electric-thermal load and the output power of wind power generation and photovoltaic power generation are shown in Fig. 2. Six types of time-shiftable loads are selected to form the TSL cluster, and the size of the unit demand of different types of time-shiftable loads is shown in Fig. 3. The peak hour tariff, weekday tariff and valley tariff are 0.83($/kW·h), 0.49($/kW·h) and 0.25($/kW·h), respectively. The system facility operating parameters are shown in Table 1. The electrical and thermal energy storage parameters are shown in Table 2. It should be noted that these basic data can refer to^57,58,59.

Figure 2

Raw demand characteristics and wind and PV output power.

Figure 3

Various TSL original demand characteristics.

Table 1 Operating parameters related to integrated regional energy systems.

Table 2 Electrical/thermal energy storage parameters.

The example is based on a scheduling cycle of 24 h a day, with a unit scheduling time of 1 h, where a group aggregation model consisting of 6 types of loads is involved in the demand response under the incentive response and the number of each type of load is taken as 50, and the maximum number of consecutive scheduling periods for flexible thermal loads is taken as T′ = 3. The superiority of the proposed integrated demand response model is verified by simulation.

Results: case studies

In order to verify the feasibility of the integrated electricity-thermal demand response considering the expectation curve of dispatchers proposed in this paper, the electricity-thermal response under three different cases is compared and analyzed.

• Case 1: Consider only the response of integrated electric-thermal energy substitution without considering the dispatchable value of electric-thermal load;

• Case 2: Also consider the electric-thermal integrated energy substitution response and the electric load response with the participation of TSL tracking and scheduling signals, without considering the thermal load participation response;

• Case 3: Also consider the integrated electricity-heat energy substitution response and the integrated electricity-heat demand response of TSL tracking dispatch signals.

The scheduling results of the IES of the park for three different cases are shown in Table 3.

Table 3 Total system operating cost, new energy utilization in different cases.

A comparative analysis of Table 3 shows that the total operating cost of the IES is lower in Case 3 than in Cases 1 and 2. The cost of Case 3 considering the combined electric-thermal demand response is 9389.3$, which is 396.1$ lower than the cost considering only the alternative response under Case 1, and 117.9$ lower than the electric load response considering the dispatcher's desired signal under Case 2. For wind and solar energy, there is a substantial increase in utilization rate. After considering the integrated electricity-thermal demand response, the utilization rate of wind energy increases by 32.41% and 10.68%, and the utilization rate of solar energy increases by 20.46% and 8.79%, respectively, compared with Case 1 and Case 2, and the utilization rate of wind energy increases more. It shows that after considering the integrated electricity-thermal demand response, the operating cost of the system can be reduced and the utilization of wind and solar energy within the system is improved.

Discussion

The output curves of each unit for different cases of electrical and thermal load balancing are shown in Figs. 4, 5, 6, 7, 8 and 9.

Figure 4

Case 1: Electric load balance output curve of each unit.

Figure 5

Case 1: Heat load balance output curve of each unit.

Figure 6

Case 2: Electric load balance output curve of each unit.

Figure 7

Case 2: Heat load balance output curve of each unit.

Figure 8

Case 3: Electric load balance output curve of each unit.

Figure 9

Case 2: Heat load balance output curve of each unit.

From Figs. 4, 5, 6, 7, 8 and 9, it can be seen that the system can achieve the complementary use of electricity-thermal energy under the multi-energy complementary alternative response in Case 1. Increase cogeneration output when electricity prices are high and purchase electricity from the grid when prices are low. The system can control the power output and start/stop status of each distributed unit to ensure the most economical operation. At this time the electric storage will be charged at the valley tariff, supplemented once at the usual tariff, and discharged at the peak tariff. Electric heating saves the system's energy costs by increasing electricity use during low electricity prices to reduce the natural gas consumption of the gas boiler. Compared to Case 1, where only alternative response participation is considered, Case 2 and Case 3 increase the peak hour demand from 432.74 to 519.28 kW and 470.28 kW, respectively, and reduce the peak hour demand from 904.48 to 789.98 kW and 829.82 kW. It is shown that the electric load response considering the dispatch expectation signal and the integrated electric-thermal demand response can better achieve peak-shaving and valley-filling on the customer side. At the same time, in Case 2, the controllable flexible load is fully utilized by the load following the dispatch signal, and the fluctuation of unit output is smoothed. In Case 1, the CHP unit's output fluctuates greatly, and the flexibility of the unit is reduced by the "heat-and-power" operation mode. In Case 3, the unit has one fluctuation at noon when the PV output is high, and the rest of the time it runs more smoothly with less fluctuation in output. At this time, the electric energy storage will accommodate part of the new energy output and the discharge moment will also be earlier than in case 1. The electric heating system not only provides continuous heating at low electricity prices but also increases the output at normal electricity prices due to load changes, making the coupling of the heat and power system stronger and the cooperation of each unit more flexible.

The wind and solar power output curves for different cases are shown in Figs. 10, 11 and 12.

Figure 10

Case 1: Wind and solar energy accommodation curves.

Figure 11

Case 2: Wind and solar energy accommodation curves.

Figure 12

Case 3: Wind and solar energy accommodation curves.

From Figs. 10, 11 and 12, we can see that the accommodation of wind and solar energy is higher at night in the three cases, and the heat supply is also at its peak at night, when the CHP units and electric heat production will be influenced by the "heat to power" operation mode to increase the output and improve the space for new energy accommodation. Under Case 1, the utilization of wind and solar energy is low, with wind and light abandonment rates of 38.14% and 30.20%, respectively. In Case 2, the load shifting due to the load-tracking scheduling signal leads to an increase in load at the valley tariff and the usual tariff, thus reducing the abandoned wind and solar rates to 16.41% and 18.53%. In Case 3, the optimization of the electric-thermal load curve and the coordination of the output of the CHP unit and the electric heat boiler further reduce the abandoned wind and solar energy rates to 5.73% and 9.74% when considering both the incentive response and the thermal load response of the dispatcher's desired signal.

The response of the electric load following the dispatch signal and the flexible thermal load participating in the optimal dispatch are shown in Figs. 13 and 14.

Figure 13

Case 2: Electricity load follows the change of dispatch signal.

Figure 14

Case 2: Flexible thermal load scheduling situation.

From Figs. 13 and 14, it can be seen that the electric load can reduce the peak-to-valley difference of the electric load while tracking the dispatch signal, which can play the role of peak-shaving and valley-filling of the IES and improve the flexibility and reliability of the system operation by smoothing the load fluctuation. The load response curves in Fig. 13 show that during the midday and evening hours, the portion of the load that uses more electricity and has a higher tariff is shifted to the valley hour tariff and the usual tariff hours. Figure 14 shows the flexible thermal load participation, which fully exploits the ability of the end-use thermal load to participate in the response while ensuring customer satisfaction with energy use. The economic cost of the system is optimized by considering the electric-thermal coupling and ensuring the heat demand.

In order to verify the superiority of the algorithm in this paper, in case 3, the traditional GWO^60,61 and the Improved Particle Swarm Optimizer (IPSO)^62,63 are used to compare with IGWO. It should be pointed out that the parameters set by GWO and IPSO in the simulation experiment process can refer to these References^60,61,62,63 are given.

The optimization iteration curve comparison is shown in Fig. 15, and the optimization iteration data comparison is shown in Table 4. The initial number of wolves is 50, and the maximum number of iterations is 1000.

Figure 15

Optimize iterative curve.

Table 4 Comparison of iterative data of algorithm.

Comprehensive comparison and analysis of Fig. 15 and Table 4, in terms of the number of iterations convergence, when using traditional GWO in case 3, it converges at generation 275, when using IPSO, it converges at generation 297, and when using IGWO, it is still searching for optimization at this time, and Converged at generation 482. In terms of convergence time, when using traditional GWO in case 3, the convergence time is 259.8 s, when IPSO is used, the convergence time is 295.6 s, and when IGWO is used, the convergence time is 317.1 s, although the running time has increased compared with the former two, however, the increase is small and within an acceptable range. In terms of total system operation cost, in case 3, when GWO is used, the total system operation cost is 9943.5$, when IPSO is used, the system operation cost is 9675.2$, and when IGWO is used, the system operation cost is 9389.3$, which are lower than their respective 554.2$ and 285.9$. Therefore, the total system operating cost obtained with IGWO is much better. In summary, IGWO can improve the deficiencies in the lack of diversity of the subsequent population of evolution, so that the population diversity in the process of evolution can maintain better, while doing exceptional speed, improve the algorithm jump out of local optimal ability to achieve continuous deep search.

Conclusion

Based on the electric load dispatching model, this paper further considers the dispatching value of heat load participating in demand response, and establishes an electric-heat integrated demand response model. In order to verify the validity of the proposed electrothermal comprehensive demand response model, three different cases were set up for simulation comparison analysis. At the same time, in order to verify the superiority of IGWO, the simulation comparison analysis was carried out with traditional GWO and IPSO, and the results showed that:

• (1) When only considering the electric-heat substitution response, the system can cut peaks and fill valleys within a certain range, but the operating cost is high and the utilization rate of new energy is low.

• (2) When considering the dispatcher's expected signal and electric load response, the system can achieve peak shaving and valley filling, and appropriately increase the electric load demand when the heat demand is large at night, which can improve the accommodation level of new energy.

• (3) When considering the integrated electric and heat demand response of the dispatcher's desired signal, the operating cost of the system can be reduced to a greater extent, the utilization rate of new energy can be improved, and the benign interaction between the source and the load can be promoted.

• (4) IGWO can improve the defect of insufficient population diversity in the later stage of evolution, so that the population diversity can be better maintained during the entire evolution process. While taking into account the speed of optimization, it improves the algorithm's ability to jump out of the local optimum and realizes continuous deep search.

Since the uncertainty on both sides of the source-load affects the reliability and economy of the system operation, the integrated demand response of the system under multiple uncertainties will be considered in the subsequent research work.