Abstract
We present a detailed study regarding the bandgap dependence on diameter and composition of spherical Ge-rich GexSi1−x nanocrystals (NCs). For this, we conducted a series of atomistic density functional theory (DFT) calculations on H-passivated NCs of Ge-rich GeSi random alloys, with Ge atomic concentration varied from 50 to 100% and diameters ranging from 1 to 4 nm. As a result of the dominant confinement effect in the DFT computations, a composition invariance of the line shape of the bandgap diameter dependence was found for the entire computation range, the curves being shifted for different Ge concentrations by ΔE(eV) = 0.651(1 − x). The shape of the dependence of NCs bandgap on the diameter is well described by a power function 4.58/d1.25 for 2–4 nm diameter range, while for smaller diameters, there is a tendency to limit the bandgap to a finite value. By H-passivation of the NC surface, the effect of surface states near the band edges is excluded aiming to accurately determine the NC bandgap. The number of H atoms necessary to fully passivate the spherical GexSi1−x NC surface reaches the total number atoms of the Ge + Si core for smallest NCs and still remains about 25% from total number of atoms for bigger NC diameters of 4 nm. The findings are in line with existing theoretical and experimental published data on pure Ge NCs and allow the evaluation of the GeSi NCs behavior required by desired optical sensor applications for which there is a lack of DFT simulation data in literature.
Similar content being viewed by others
Introduction
SiGe being one of the most studied semiconductor alloy continues to be in front of the developing researches for many microelectronics and optoelectronics applications. For high-speed SiGe CMOS technology, the SiGe heterojunction bipolar transistors achieved record performances1,2. On the other hand, the integrated photonics based on elements Si-Ge-Sn from group IV is experiencing a pronounced increase in the research activity in the field. Thus, the SiGe light detectors can extend their sensitivity in short-wave infrared range3. However, there is a low efficiency of light emission and band-edge absorption in SiGe large crystals due to the indirect bandgap character and necessary participation of phonons to the optical transitions. The efficiency can be improved by quantum confinement in NCs or by Sn alloying or by strain engineering to obtain direct bandgap in (Si)GeSn4,5,6,7,8. Versatile techniques were developed for embedding Ge and GeSi NCs in oxides for fabrication of optoelectronic devices benefiting from the advantages of materials and technology, namely the compatibility with CMOS technology and cost-effective fabrication, while being environmentally friendly. Also, they are a very advantageous alternative to III–V semiconductors for optoelectronic devices. The most interesting applications based on Ge and GeSi NCs are in optoelectronics and nanophotonics, i.e. photodetectors9,10,11, LEDs12, non-linear optics applications13 and energy harvesting devices14,15.
Quantum confinement effect was evidenced in small Ge and GeSi NCs16,17,18, enabling bandgap engineering along with composition19, shape20 and strain21,22 leading to tuning of optical and photoelectrical properties of NCs.
It was shown that two mechanisms compete in achieving no-phonon radiative transitions in NCs of Si and Ge that are indirect bandgap semiconductors in bulk. One mechanism is related to the relaxation of momentum conservation law due to the spatial confinement and Heisenberg uncertainty principle, being dominant in both Si and Ge NCs, and the other mechanism is the inter-valley coupling between direct and indirect states induced by the interface of the NC with the embedding matrix23. Another way of bandgap tuning is by tailoring its level of directness, as recently demonstrated direct bandgap light emission in Ge and GeSi nanowires with hexagonal structure5,24, and GeSi quantum dots25 and also by infrared detection extended to longer wavelengths in NCs of direct bandgap GeSn alloys26.
Strong quantum confinement effect is expected in Ge NCs as the Bohr exciton radius is 24 nm, thus facilitating the bandgap tuning by tailoring the NCs size in relatively large NCs27,28. Moreover, by alloying Ge with Si, GeSi NCs are more thermally stable than Ge NCs by impeding the fast diffusion of Ge during nanocrystallization by annealing29. Alloy GeSi NCs benefit from the complete miscibility of Ge with Si over the whole composition range, while maintaining the same crystalline structure20. The miscibility and intermixing of Ge and Si in GeSi random alloys can be associated to the strong self-diffusion that is theoretically explained by the vacancies formation and their contribution to the diffusion processes30,31. The vacancies formation energy reduces for high Ge concentration30 increasing the diffusion coefficient as experimentally proved32. By employing DFT computation it was shown that the local electronegativity of the defects is strongly dependent upon the nearest neighbor environment33.
Theoretical and numerical studies in the frame of DFT are valuable tools to complement experimental data and better understand the results, providing new insights in the development of nanomaterials with targeted properties.
With respect to GeSi nanostructures, it was shown based on calculated density of states (DOS) that the absorption edge of small Si and Ge NCs (0.6–1.0 nm) embedded in SiO2 is dependent on their size34. A study of structural and electronic properties of hydrogenated Si and Ge nanowires and Si, Ge, Si/Ge NCs (0.8 to 2.4 nm) shows that encapsulated Ge NCs could act as optical absorption centers in the infrared region35. The study on the structural stability of H-passivated GeSi NCs by calculating formation enthalpies of different GexSiyHz isomers reveals that most stable GeSi:H NCs are the ones with the lowest formation enthalpy and widest bandgap36. The theoretical works from literature report results on small diameter range Ge NCs (1–2 nm), only, in contrast to experiments dealing with larger GeSi NCs29,37,38,39. Thus, there is a lack of theoretical DFT investigation on SiGe NCs of commonly experimentally observed spherical shape and for a wide range of compositions and sizes.
In this work, we present first principles electronic DOS and energy gap DFT calculations on spherical H-passivated GeSi NCs with large ranges of Ge content (50–100%) and NCs diameter (1–4 nm). A composition invariance of the line shape of the bandgap diameter dependence was found for the whole diameter and composition computation range. For comparison with experimental bandgap values and to be used for the design and characterization of optoelectronic devices based on GeSi NCs, the bandgap diameter dependences of different GeSi NC compositions are extrapolated to larger NCs by considering the asymptotic bulk values.
Results and discussion
Structure of spherical Ge and GeSi NCs
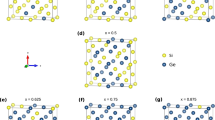
For DFT calculations, spherical NCs of Ge and GeSi with different Ge contents (50%, 75%, 90% and 95%) were constructed using in-house software. The initial coordinates of Ge and Si atoms in NCs correspond to the bulk cubic Ge lattice (space group Fd-3m) with a lattice constant of 5.66 Å. GeSi NC is built in a similar way as Ge NC, but Ge atoms are randomly substituted by Si atoms to obtain the desired Ge concentration. The generated GeSi spheres have diameters in the 1.25–3.96 nm range. For the x = 100% Ge case, Fig. 1a–c shows small, medium and large Ge NCs, respectively, projected along [100] and [110] directions. Facets are clearly revealed especially for images of the [100] orientation.
(a–e) Relaxed Ge:H NC model in atomistic simulations: (a) small (1.47 nm diameter), (b) medium (2.83 nm) and (c) big NCs (3.96 nm); (d) atomic coordinates based on Ge tetrahedral symmetry; (e) surface detail of relaxed Ge:H NC. (f) Model for relaxed GeSi:H NC with 50:50 Ge:Si composition. Models are produced by VESTA41.
The surface of both Ge and GeSi NCs was passivated with H atoms (annihilating dangling bonds effects in Ge:H and GeSi:H NCs). In the Ge NC, the H atoms are positioned in the vertices of Ge tetrahedron or out of tetrahedron depending on the number of Ge dangling bonds (Fig. 1d). Similarly, in GeSi NC, H atoms are positioned at Ge or Si dangling bonds. After geometrical construction, the H-passivated NCs are subjected to the energetic relaxation by atomistic computations as described in the “Methods” section. In a relaxed Ge NC, the Ge–H bond length is 1.56 Å, while Ge–Ge length is 2.42 Å close to the bulk value of 2.45 Å40, as seen in the surface detail of Fig. 1e.
The geometric construction of energetically relaxed H-passivated GeSi NC with x = 50% is exemplified in Fig. 1f. Further details are given in “Methods” section and Supporting Information (SI)—Table S1.
The passivation of NC surface is mandatory for excluding any surface localized states near the band edges as the calculations focus on the bandgap23, but also to ensure the computation convergence. The diameter dependences of the number of H atoms and the number of Ge and Si atoms in each NC (listed in Table S1 in SI) resulting from the model are shown in Fig. 2. In Fig. 1, one can see that Ge and Si atoms in NCs do not perfectly fill the spherical shape. However, the mean density of 44.0 atoms/nm3 of Ge and substituting Si atoms (Fig. 2) uniformly distributed in spherical NCs that fits well the diameter dependence of the constructed NCs is slightly smaller than Ge bulk value of 44.1 atoms/nm3.
NC diameter dependences of the number of Ge and substituting Si atoms (blue dots), and the number of H atoms (red squares) necessary to construct the model of GeSi:H NCs with fully passivated surface; the continuous lines correspond to 44.0 atoms/nm3 atomic density for Ge and Si and to 10.8 atoms/nm2 for H surface density uniformly distributed on spherical GeSi:H NCs. The inset shows the concentration of H passivation atoms in NC.
It is obvious that these results are independent of Si at.% content taking into account the similar way in which the atomic coordinates of both Ge and GeSi NCs are generated. The concentration of H at.% required for complete passivation of the NC surface reaches quite high values, more than 50% for small diameters and is still 25% high for the NC size of 4 nm and corresponds to the mean value of 10.8 atoms/nm2 in the spherical NC (inset in Fig. 2).
Diameter dependence of the Ge NCs bandgap
Spherical Ge NCs passivated with H atoms, with diameters from 1.25 to 3.96 nm were considered in the atomistic simulation. A cumulative DOS plot of Ge NCs is shown in Fig. 3, revealing the decrease of energy gap with the increase of NC diameter.
The calculated energy gap Eg of Ge NCs is presented in Fig. 4 and in Table 1. The energy gap dependence on diameter can be described by a power law asymptotic to the bandgap of bulk Ge, for diameters higher than 2 nm:
where α = 1.25 ± 0.02 and A = 4.58 ± 0.14 eV are the fit parameters, d is expressed in nm and Egbulk = 0.66 eV is the experimental value, close to theoretical bandgap of 0.63 eV calculated by us using DFT in local density approximation (LDA). The accuracy assessment of LDA and generalized gradient approximation (GGA) methods is made by band structure computation of bulk Ge and Si. As can be seen in Figure S1 in SI the LDA computation gives a smaller bandgap for Ge with a low error of 30 meV in respect to the experimental value, while the GGA gives a much lower value of bandgap of 0.47 eV (200 meV error). For bulk Si, both methods give a bandgap almost 200 meV higher than the experimental value. Therefore, for the DOS calculation in GeSi NCs presented in the next section, we used the LDA calculation method and we limited the composition to the range of 50—100% Ge.
Ge NCs energy gap dependence on diameter: DFT calculations (filled blue circles for calculated points and dashed blue line for fit function in Eq. 1) and experimental data from optical absorption42,43, spectral photocurrent42 and scanning tunneling spectroscopy (STS)44 for which filled, empty and half-filled squares correspond to different capping ligands.
If the 0.63 eV theoretical gap is considered, the fit results are quite similar to that of the asymptotic experimental value of 0.66 eV. The fit curve extrapolated to higher diameters (15 nm) is shown in Fig. 4. One can see that our results fit well the experimental values from literature obtained by different methods such as optical absorption42,43, spectral photocurrent42 and scanning tunneling spectroscopy (STS)44. The standard deviation of the experimental results with respect to the fit has a reasonable value of σ = 0.12 eV, taking into account that the experimental NCs usually have a quite broad size distribution.
Figure 5a shows a comparison of our calculated energy gaps (DFT–LDA) with other theoretical energy gaps for Ge NCs from literature obtained by using DFT45,46, tight binding (TB)45, \(\mathbf{k}\cdot \mathbf{p}\) and empirical pseudopotentials methods47. One can remark that the power law dependence (Eq. 1) overlaps the whole 1–12 nm diameter interval with the TB results45. Other computation methods show significant deviation from our results at small diameters (e.g. empirical pseudopotentials and \(\mathbf{k}\cdot \mathbf{p}\)), but all methods show a good agreement at diameters higher than ~ 8 nm.
Energy gap dependence on diameter obtained in the frame of different calculations: (a) our DFT results (blue filled circles for calculated points and dashed line for the power law dependence in Eq. 1) compared to reported results obtained by DFT45,46, TB45,\(\mathbf{k}\cdot \mathbf{p}\)45 and empirical pseudopotentials47; (b) our DFT data compared to others45,46,48,49.
The comparison of DFT results for the 1–4 nm diameter range is shown in Fig. 5b. One can see that we obtain similar results with those from Ref45 that were however obtained only for very small diameters in the 1.27–1.90 nm range.
Related to the effect of passivation on the bandgap, it was experimentally shown44 that the effect of capping ligand is not measurable, but it can change the Fermi level within the band gap. Our computations have shown that the Fermi level of H-passivated Ge NCs is close to the middle of the bandgap, as expected for intrinsic and well passivated semiconductor NCs. In fact, the Fermi level can be significantly moved towards conduction or valence bands by doping defects (vacancies or dopant atoms).
The type of passivation is of a great importance for the optoelectronic properties of the NCs. In experiments, NCs are often embedded in a dielectric matrix, the surface not being H-passivated necessarily. By H-passivation of NC surface, the effect of surface states near the band edges is excluded aiming to accurately determine NC bandgap. The H-passivation of spherical NCs is easily performed using our in-house developed code for the construction of NCs and has the advantage to fully passivate the free Ge bonds at NCs surface, as well as to remove the surface states from the bandgap region that is similar to the effect that takes place in amorphous hydrogenated Si. The software can also be used for O-passivation by replacing H atoms, but in this case the O atoms are placed only at sides where two Ge free bonds can be passivated by a single O atom, the rest of free Ge bonds on the NC surface remaining passivated by H atoms. We expect O–Ge bonds to produce stronger deformation of the Ge lattice at the NCs surface, resulting in some changes of the bandgap in respect to the case of the passivation with H only. DFT computations in progress will show the effect of the type of passivation atoms on the NCs bandgap.
Diameter dependence of the GeSi NCs bandgap
Besides NC size, the alloy GexSi1−x NCs provide an additional parameter, namely the composition for bandgap control over a spectral range wider than that of Ge NCs. We focus our attention on Ge-rich GexSi1−x NCs because of the interest to keep the optical absorption edge and bandgap related cut-off wavelength of spectral photocurrent at longer wavelengths to be compared with reported experimental results up to 1700 nm wavelengths29. Thus, in DFT calculations of DOS and energy gap, we consider Ge at.% concentrations of 95, 90 and 75 at.% Ge in H-passivated GeSi NCs. The results are compared with those for stoichiometric GeSi (50:50) and pure Ge NCs by varying the NC diameter d from 1.25 to 3.96 nm as presented in Table 1. Due to the constraint of the numerical construction of spherical GexSi1−x NCs, the Ge concentration cannot be kept strictly constant for the whole range of diameters, the standard deviation being about 0.3% (Table S1 in SI).
Cumulative calculated DOS spectra for H-passivated GeSi NCs with 50% Ge concentration are given in Fig. 6 showing the energy gap decrease with diameter increase similarly as for Ge NCs.
The calculated diameter dependence of the bandgap of GeSi (50:50) NC is compared to that for Ge NCs in Fig. 7a. In a similar way as for Ge NCs, the computed energy gap values for each diameter are well described by the empirical power law dependence (Eq. 1) for diameters higher than 2 nm. As can be seen (Fig. 7a), for both cases at diameters smaller than 2 nm, the increase of the bandgap shows a tendency of upper limitation that can be caused by the finite value of the difference between bonding and antibonding energies.
(a) and (b) Diameter dependence of bandgap Eg(d) of GexSi1−x NCs for different Ge at.% concentrations obtained by DFT calculations: symbols—calculated points, fit curve—continuous lines with Eq. (1); fit parameters A and α—inset in figure (b); Eg fit curves show a tendency of upper limitation for diameters smaller than 2 nm—dashed lines in figure (a). (c) Size dependences of the computed Eg(d) shifted on vertical by subtracting 0.651(1 − x) in eV units: Eg(d,x) = E0NC(x) + A/dα, E0NC = 0.66 + 0.651(1 − x), A = 4.58 eV, α = 1.25; (d) E0NC parameter of the cumulative fit of all computed data is compared with Egbulk of GexSi1−x alloys from Ioffe data50.
The fit curves using Eq. (1) for each Ge concentration of GeSi NC are shown in Fig. 7b, and corresponding fit parameters A, α and Egbulk are given in inset. The experimental dependences of Egbulk (dependent on Ge concentration) for asymptotic values are taken from the Ioffe database50 (also in Fig. 7d). Moderate fluctuations of the fit parameters A and α are obtained (inset in Fig. 7b). This suggests that the shape of diameter dependence curve of GeSi NCs energy gap is slightly dependent on the Ge concentration over the explored composition range. Indeed, if all computed Eg(d) curves are vertically shifted by subtracting 0.651(1 − x) term dependent on Ge concentration x, the data are well superposed over the curve for Ge NCs, shown in Fig. 7c. It results that the computed band gap Eg(d,x) of GexSi1−x NCs as a function of diameter d and Ge concentration x can be approximated by Eg(d,x) = EgGe(d) + 0.651(1 − x) in which EgGe(d) is the bandgap diameter dependence for pure Ge NCs. This invariance of the shape of the computed bandgap valid for the whole explored diameters (1.6–3.9 nm) and composition range (Fig. 7c) is well described by a power function as that of Eq. (1):
with E0NC = 0.66 + 0.651(1 − x) instead of Egbulk (Eq. 1). This asymptotic E0NC to larger NCs deviates from the bulk value Egbulk up to 0.1 eV and does not reflect the influence of the change from L to X minimum of the conduction band in bulk GeSi alloys (the knee observed at 90% Ge in Fig. 7d). It is what we can expect as a result of confinement effect in NCs that removes the indirect bandgap character by relaxation of the momentum conservation law.
Conclusions
Spherical H-passivated Ge-rich GexSi1−x NCs with Ge atomic concentration in the range of 50–100% and diameters from 1 to 4 nm were theoretically studied by atomistic DFT calculations using the SIESTA software. The results serve to fill the gap in literature regarding theoretical investigations on electronic band structure of GeSi NCs. The GeSi NCs were constructed using an in-house developed code by taking into account the tetrahedral symmetry (space group Fd-3m) of cubic Ge(Si). The spheres have been filled with Ge and Si atoms in the cubic Ge coordination and subjected to lattice relaxation after the H-passivation of the NCs surface. The number of H atoms necessary to fully passivate the NC surface reaches the number of Ge core atoms for smallest NCs and still remains of about 25% for 4 nm size. The computed DOS for different concentrations and diameters has been used for obtaining the NC bandgap as a function of the diameter for different Ge concentrations. It was found that the shape of Eg(d,x) is almost independent on composition for the whole investigated diameter-composition range being described by Eg(d,x) = EgGe(d) + 0.651(1 − x), in which EgGe(d) is the bandgap of Ge:H NCs. For diameters from 1.6 to 4 nm, the shape of the bandgap dependence on diameter can be fitted by a power function EgGe(d) = 0.66 + 4.58/d1.25, and shows a tendency of upper bandgap limitation for smaller diameters. The extrapolation to the bulk bandgap value of Eg(d,x) fit curves can be used for the design and characterization of optoelectronic devices based on GeSi NCs.
Methods
All atomistic simulations were performed using the SIESTA code51 in order to take advantage of the localized basis functions (numerical atomic orbitals) leading to linear scaling of computation time with the dimensions of the atomistic model. The computations were performed with LDA for the exchange–correlation energy functional.
The atomic coordinates of spherical GexSi1−x NC (for each considered Ge concentration x) were generated by considering a cubic simulation cell of 10 nm edge length in which the NC surrounded by vacuum is centered. The simulation cell acts as the unit cell in periodic boundary conditions computations. This configuration is necessary because the overlap of electronic wave functions belonging to neighboring NCs must vanish.
LDA pseudopotentials for valence electrons 4s2 4p2 of Ge, 3s2 3p2—Si and 1s1—H were employed, respectively. The calculations were done using a double-zeta basis size, i.e. two basis functions for each numerical atomic orbital, with a 150 Ry mesh cut-off, a limit of 50 steps for self-consistent field loop with a convergence tolerance of 10–3 for the elements of the density matrix and 10–4 for the elements of the Hamiltonian matrix. The convergence criteria refer to the simultaneous self-consistency of the density matrix and the Hamiltonian matrix. The self-consistency of the density/Hamiltonian matrix is achieved when the maximum difference between the output and the input on each element of the density/Hamiltonian matrix in a SCF loop is smaller than the respective tolerance. The passivation of NC surface is mandatory for excluding surface localized states, but also to ensure the convergence of the DFT-SIESTA computation. According to folding zone theory, for NCs the calculations are done in Γ point, only.
Total energy was computed by diagonalization of the effective Kohn–Sham Hamiltonian, for 300 K electronic temperature of the occupation function (Fermi–Dirac distribution). For geometrical relaxation of NCs, we employed the conjugate gradient method with a maximum atomic displacement of 0.1 Å and the stop criteria of either 50 relaxation steps or a force tolerance of 0.1 eV/Å. DOS was calculated for each NC, per unit energy and per unit volume, ignoring electronic spin, as \(g\left(E\right)=\sum _{i}\delta \left({\varepsilon }_{i}-E\right)\), where \({\varepsilon }_{i}\) are the eigenvalues of the effective Kohn–Sham Hamiltonian, in the range between − 15 eV and 10 eV using 1000 points, with a broadening of 0.150 meV. The set of eigenvalues yields the energy gap as the difference of the two eigenvalues adjacent to the Fermi level.
References
Mooney, P. M. & Chu, J. O. SiGe technology: Heteroepitaxy and high-speed microelectronics. Annu. Rev. Mater. Sci. 30, 335–362 (2000).
Rücker, H. & Heinemann, B. High-performance SiGe HBTs for next generation BiCMOS technology. Semicond. Sci. Technol. 33, 114003 (2018).
Benedikovic, D. et al. Silicon–germanium receivers for short-wave infrared optoelectronics and communications. Nanophotonics 10, 1059–1079 (2021).
Priolo, F., Gregorkiewicz, T., Galli, M. & Krauss, T. F. Silicon nanostructures for photonics and photovoltaics. Nat. Nanotechnol. 9, 19–32 (2014).
Fadaly, E. M. T. et al. Direct-bandgap emission from hexagonal Ge and SiGe alloys. Nature 580, 205–2019 (2020).
Rainko, D. et al. Investigation of carrier confinement in direct bandgap GeSn/SiGeSn 2D and 0D heterostructures. Sci. Rep. 8, 15557 (2018).
Stange, D. et al. Optical transitions in direct-bandgap Ge1−xSnx alloys. ACS Photonics 2, 1539–1545 (2015).
Iancu, V. et al. Calculation of the quantum efficiency for the absorption on confinement levels in quantum dots. J. Nanoparticle Res. 13, 1605–1612 (2011).
Shi, S., Zaslavsky, A. & Pacifici, D. High-performance germanium quantum dot photodetectors: Response to continuous wave and pulsed excitation. Appl. Phys. Lett. 117, 251105 (2020).
Dhyani, V., Ahmad, G., Kumar, N. & Das, S. Size-dependent photoresponse of germanium nanocrystals-metal oxide semiconductor photodetector. IEEE Trans. Electron Dev. 67, 558–565 (2020).
Palade, C., Stavarache, I., Stoica, T. & Ciurea, M. L. GeSi nanocrystals photo-sensors for optical detection of slippery road conditions combining two classification algorithms. Sensors 20, 6395 (2020).
Li, Y. et al. Precisely ordered Ge quantum dots on a patterned Si microring for enhanced light-emission. Nanotechnology 31, 385603 (2020).
Zhigunov, D. M., Evlyukhin, A. B., Shalin, A. S., Zywietz, U. & Chichkov, B. N. Femtosecond laser printing of single Ge and SiGe nanoparticles with electric and magnetic optical resonances. ACS Photonics 5, 977–983 (2018).
Tkalčević, M. et al. Ge quantum dot lattices in alumina prepared by nitrogen assisted deposition: Structure and photoelectric conversion efficiency. Sol. Energy Mater. Sol. Cells 218, 110722 (2020).
Basioli, L. et al. Ge quantum dots coated with metal shells (Al, Ta, and Ti) embedded in alumina thin films for solar energy conversion. ACS Appl. Nano Mater. 3, 8640–8650 (2020).
Lehninger, D., Beyer, J. & Heitmann, J. A review on Ge nanocrystals embedded in SiO2 and high-k dielectrics. Phys. Status Solidi A 215, 1701028 (2018).
Barbagiovanni, E. G., Lockwood, D. J., Simpson, P. J. & Goncharova, L. V. Quantum confinement in Si and Ge nanostructures: Theory and experiment. Appl. Phys. Rev. 1, 011302 (2014).
Ciurea, M. L. Quantum confinement in nanocrystalline silicon. J. Optoelectron. Adv. Mater. 7, 2341–2346 (2005).
Barth, S., Seifner, M. S. & Maldonado, S. Metastable group IV allotropes and solid solutions: Nanoparticles and nanowires. Chem. Mater. 32, 2703–2741 (2020).
Bonham, B. & Guisbiers, G. Thermal stability and optical properties of Si-Ge nanoparticles. Nanotechnology 28, 245702 (2017).
Zinovyev, V. A. et al. Strain-induced improvement of photoluminescence from the groups of laterally ordered SiGe quantum dots. Appl. Phys. Lett. 110, 102101 (2017).
Chen, Q. et al. Highly tensile-strained self-assembled Ge quantum dots on InP substrates for integrated light sources. ACS Appl. Nano Mater. 4, 897–906 (2021).
Ji, Z.-M., Luo, J.-W. & Li, S.-S. Interface-engineering enhanced light emission from Si/Ge quantum dots. New J. Phys. 22, 093037 (2020).
Amato, M., Kaewmaraya, T. & Zobelli, A. Extrinsic doping in group iv hexagonal-diamond-type crystals. J. Phys. Chem. C 124, 17290–17298 (2020).
Zinovieva, A. F. et al. Photoluminescence of compact GeSi quantum dot groups with increased probability of finding an electron in Ge. Sci. Rep. 10, 9308 (2020).
Slav, A. et al. GeSn nanocrystals in GeSnSiO2 by magnetron sputtering for short-wave infrared detection. ACS Appl. Nano Mater. 2, 3626–3635 (2019).
Ray, S. K., Maikap, S., Banerjee, W. & Das, S. Nanocrystals for silicon-based light-emitting and memory devices. J. Phys. D: Appl. Phys. 46, 153001 (2013).
Ciurea, M. L. & Lepadatu, A. M. Tuning the properties of Ge and Si nanocrystals based structures by tailoring the preparation conditions. Dig. J. Nanomater. Biostruct. 10, 59–87 (2015).
Lepadatu, A.-M. et al. Influence of SiGe nanocrystallization on short-wave infrared sensitivity of SiGe–TiO2 films and multilayers. J. Phys. Chem. C 124, 25043–25053 (2020).
Venezuela, P., Dalpian, G. M., da Silva, A. J. R. & Fazzio, A. Vacancy-mediated diffusion in disordered alloys: Ge self-diffusion in Si1−xGex. Phys. Rev. B 65, 193306 (2002).
Saltas, V., Chroneos, A. & Vallianatos, F. Composition and temperature dependence of self-diffusion in Si1−xGex alloys. Sci. Rep. 7, 1374 (2017).
Kube, R. et al. Composition dependence of Si and Ge diffusion in relaxed alloys. J. Appl. Phys. 107, 073520 (2010).
Christopoulos, S.-R.G., Kuganathan, N. & Chroneos, A. Electronegativity and doping in Si1−xGex alloys. Sci. Rep. 10, 7459 (2020).
Ossicini, S., Amato, M., Guerra, R., Palummo, M. & Pulci, O. Silicon and germanium nanostructures for photovoltaic applications: Ab-initio results. Nanoscale Res. Lett. 5, 1637–1649 (2010).
Marri, I., Amato, M., Guerra, R. & Ossicini, S. First principles modeling of Si/Ge nanostructures for photovoltaic and optoelectronic applications. Phys. Status Solidi B 255, 1700627 (2018).
Qiu, S.-B., Wang, Y.-T., He, C.-C., Deng, X.-L. & Yang, X.-B. Structural stabilities and optical properties of SixGeyHz nanocrystals. Phys. Lett. A 384, 126597 (2020).
Ha, N. N. et al. Single phase Si1−xGex nanocrystals and the shifting of the E1 direct energy transition. Nanotechnology 26, 375701 (2015).
Stavarache, I. et al. SiGe nanocrystals in SiO2 with high photosensitivity from visible to short-wave infrared. Sci. Rep. 10, 3252 (2020).
Sultan, M. T. et al. Enhanced photoconductivity of SiGe nanocrystals in SiO2 driven by mild annealing. Appl. Surf. Sci. 469, 870–878 (2019).
Kajiyama, H., Muramatsu, S., Shimada, T. & Nishino, Y. Bond-length relaxation in crystalline Si1−xGex alloys: an extended x-ray-absorption fine-structure study. Phys. Rev. B 45, 14005–14010 (1992).
Momma, K. & Izumi, F. VESTA-3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Lepadatu, A.-M. et al. Dense Ge nanocrystals embedded in TiO2 with exponentially increased photoconduction by field effect. Sci. Rep. 8, 4898 (2018).
Zhu, X., ten Brink, G. H., de Graaf, S., Kooi, B. J. & Palasantzas, G. Gas-phase synthesis of tunable-size germanium nanocrystals by inert gas condensation. Chem. Mater. 32, 1627–1635 (2020).
Millo, O. et al. Direct evaluation of the quantum confinement effect in single isolated Ge nanocrystals. J. Phys. Chem. Lett. 6, 3396–3402 (2015).
Niquet, Y. M., Allan, G., Delerue, C. & Lannoo, M. Quantum confinement in germanium nanocrystals. Appl. Phys. Lett. 77, 1182–1184 (2000).
Tsolakidis, A. & Martin, R. M. Comparison of the optical response of hydrogen-passivated germanium and silicon clusters. Phys. Rev. B 71, 125319 (2005).
Bulutay, C. Interband, intraband, and excited-state direct photon absorption of silicon and germanium nanocrystals embedded in a wide band-gap lattice. Phys. Rev. B 76, 205321 (2007).
Marsili, M. et al. Ab initio electronic gaps of Ge nanodots: The role of self-energy effects. J. Phys. Chem. C 117, 14229–14234 (2013).
Melnikov, D. V. & Chelikowsky, J. R. Electron affinities and ionization energies in Si and Ge nanocrystals. Phys. Rev. B 69, 113305 (2004).
Ioffe Physical-Technical Institute of the Russian Academy of Sciences, NSM Archive—Si–Ge. http://www.ioffe.ru/SVA/NSM/Semicond/SiGe/bandstr.html. Accessed 23 Mar 2021.
Soler, J. M. et al. The SIESTA method for ab initio order-N materials simulation. J. Phys: Condens. Matter 14, 2745–2779 (2002).
Acknowledgements
This work was supported by grants of the Romanian Ministry of Research, Innovation and Digitalization, CNCS—UEFISCDI, Project Numbers PN-III-P4-ID-PCE-2020-1673, PN-III-P1-1.1-TE-2016-2366, PN-III-P1-1.1-TE-2016-2050 and PN-III-P1-1.2-PCCDI-2017-0871 within PNCDI III, and NIMP Core Program PN19-03 Contract No. 21N/2019.
Author information
Authors and Affiliations
Contributions
M.L.C. proposed the research activity from which this work resulted. O.C. and G.A.N. conceived and conducted the computations. T.S., A.-M.L. O.C. and M.L.C. analyzed the results. T.S., A.-M.L, M.L.C. and O.C. wrote the manuscript. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cojocaru, O., Lepadatu, AM., Nemnes, G.A. et al. Bandgap atomistic calculations on hydrogen-passivated GeSi nanocrystals. Sci Rep 11, 13582 (2021). https://doi.org/10.1038/s41598-021-92936-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-021-92936-z
This article is cited by
-
Enhancing SiGeSn nanocrystals SWIR photosensing by high passivation in nanocrystalline HfO2 matrix
Scientific Reports (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.