Introduction

Refrigeration and air conditioning account for a large amount of the world’s energy consumption, and effective thermal management is one of the critical issues that need to be resolved if we are to achieve the United Nations Sustainable Development Goals (SDGs)1,2,3. Caloric effects of solids can provide highly efficient energy conversion without using any hazardous gases and realize innovative and environmentally friendly energy systems4,5,6,7,8,9. In the caloric effects significant entropy changes in response to external fields lead to effective thermal conversions, and magnetocaloric, electrocaloric, and barocaloric effects are typical ones induced respectively by magnetic fields, electric fields, and pressure.

Magnetocaloric effects (MCEs) have been studied extensively in recent years, and an active magnetic regenerator system working at room temperature was actually developed4,5,10,11,12. Large MCEs at room temperature were reported in some magnetic intermetallics and alloys such as Gd5Si2Ge2, FeRh, and La(Fe,Si)1313,14,15. MCEs at low temperatures also attract attention for cryogen applications like for liquefying natural gases16,17. Not only alloys but also magnetic oxides including rare earth elements with large magnetic moments were also studied as MCE materials for hydrogen liquefying, which is expected to be green fuel instead of fossil fuel18,19,20. Electrocaloric effects (ECEs), on the other hand, were found in ferroelectric and pyroelectric compounds21,22. A practical temperature change through the ECE of the multilayer capacitor of PbSc0.5Ta0.5O3 was recently demonstrated23. Besides, not only the ferroelectrics but also VO2 was found to show the ECE24.

Some of the materials showing MCEs or ECEs also show barocaloric effect (BCE)25,26,27. Because a magnetic transition in a magnetic material having a magneto-striction property can be tuned by applying pressure, its caloric property can also be utilized by applying pressure. Similarly, a phase transition in a pyroelectric material is closely related to the material’s volume change, and thus the ECE can sometimes be induced by pressure. However, practical examples of such multiple caloric effects, where more than one type of caloric effects would arise in a single sample, are rarely reported. Because the caloric effects in such materials can be driven by different applied fields, effective thermal control can be achieved in multiple ways. Moreover, in a multicaloric effect, where the caloric effect is induced in multiple fields applied simultaneously, one can expand control of thermal properties with different order parameters. The exploration of novel multiple-caloric-effect and multicaloric materials, is therefore challenging but critically important for future technologies7,8,28,29.

In this paper we report that the A-site ordered quadruple perovskite structure ferrimagnetic oxide BiCu3Cr4O12 shows giant multiple caloric effects; that is, it shows both magnetocaloric and barocaloric effects and they are large. The compound exhibits large latent heat by the first-order charge transition at 190 K, and the corresponding giant entropy change can be utilized through the magnetocaloric and barocaloric effects respectively by applying magnetic fields and pressure. Electronic instability of a mixed-valence state of the constituent transition-metal cation and strong correlation in charge–spin–lattice degrees of freedom in BiCu3Cr4O12 are crucial for giving rise to the observed multiple caloric effects.

Results and discussion

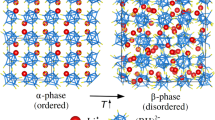
BiCu3Cr4O12 crystallizes in the A-site ordered quadruple perovskite structure, where the Bi and Cu ions are 1:3 ordered at the A site and the Cr ions are located in the center of the corner-sharing BO6 octahedra in the ABO3 perovskite structure30,31. The compound contains mixed valence Cr3.75+ at room temperature and shows charge disproportionation of Cr3.75+ to Cr3.5+ and Cr4+ at 190 K to relieve the electronic instability. As a result, the high-temperature Bi3+Cu2+3Cr3.75+4O12 phase changes to the low-temperature Bi3+Cu2+3Cr3.5+2Cr4+2O12 phase, as reported previously (Fig. 1a)32. Details of the structure characterization and the phase transition changes are given in the Supporting information (1). This charge transition behavior is in sharp contrast to the intersite charge transfer seen in LaCu3Fe4O12 and BiCu3Fe4O1233,34,35. The asymmetric displacements of Bi with lone-pair electrons stabilize the order of the charge disproportionated Cr ions32. Importantly, this charge transition is a first-order transition and produces significant latent heat. As shown in the result of differential scanning calorimetry (DSC) measurement (Fig. 1b), the observed heat flow shows thermal hysteresis of 4 K between the cooling and heating process, and the latent heat estimated from the data on cooling is 5.23 kJ kg−1 (Table S2). The corresponding entropy change is 28.2 J K−1 kg−1, which is quite large for an oxide material.

Figure 1
figure 1

(a) Crystal structure of BiCu3Cr4O12. The compound shows charge disproportionation of Cr3.75+ at the B site to Cr4+ and Cr3.5+ at 190 K. The low-temperature Bi3+Cu2+3Cr3.5+2Cr4+2O12 phase shows ferrimagnetism by the antiferromagnetic coupling of A-site Cu and B-site Cr spins. (b) DSC curves of BiCu3Cr4O12 measured in cooling (blue) and heating (red) process.

Full size image

Note also that BiCu3Cr4O12 shows a ferrimagnetic transition accompanying the charge transition and that large ferromagnetic-like (ferrimagnetic) magnetization of about 5 μB is observed below the charge disproportionation transition temperature of 190 K. The observed magnetization is close to the value reported previously (5.65 μB) but slightly smaller than that expected (6 μB) for BiCu3Cr4O12 with ferrimagnetically ordered 3Cu2+, 1Cr3+, and 3Cr4+ spins (Fig. 2a)32. The behavior of this magnetic transition is also that of a first-order transition with the thermal hysteresis of about 3.5 K (inset of Fig. 2c) and far from that of a typical second-order transition driven by the superexchange magnetic interactions36. Given a simple ferrimagnetic structure consisting of the antiferromagnetically coupled A-site Cu (Cu2+ with S = 1/2) and B-site Cr (Cr3+ with S = 3/2 and Cr4+ with S = 1) spins, a fit to the temperature-dependent magnetization data with a Brillouin function (see details in the Supporting information (3)) gives an extrapolated magnetic transition temperature of about 450 K, which is much higher than (more than double) the actual magnetic transition temperature of 190 K (Fig. 2b). The magnetic entropy, which intrinsically has to be gradually changed at temperatures below 450 K, is thus abruptly yielded by the very sharp first-order magnetic (= charge) transition. Therefore, the observed large latent heat of BiCu3Cr4O12 should be related to the magnetic entropy change, as the large latent heat of the analogue compound NdCu3Fe4O12 is related to the magnetic entropy change of that compound37. Interestingly, the magnetization curves measured under various magnetic fields keep the sharp transition behaviors, but the transition temperature linearly increases with increasing the field (Fig. 2c). The linear field coefficient for the change of ferromagnetic transition temperature is 0.101 ± 0.001 K kOe−1 (Fig. 2d). Thus, importantly, the observed large latent heat, which is related to the magnetic entropy change, can be utilized through an MCE.

Figure 2
figure 2

(a) Magnetization curve of the ferrimagnetic BiCu3Cr4O12 at 10 K. (b) Temperature dependence of magnetization for BiCu3Cr4O12 measured under 10 kOe. The red dash line represents the fitting for the total magnetization curve with the Brillouin function below the magnetic transition temperature. Contributions of Cr3+ (S = 3/2) ↑, 3Cr4+ (S = 1) ↑, and 3Cu2+ (S = 1/2) ↓ moments to the ferrimagnetization are shown in yellow, orange, and green dotted lines, respectively. (c) Temperature dependent magnetization curves for BiCu3Cr4O12 measured at various applied fields from 1 to 50 kOe in a field-cooling mode. The inset shows the thermal hysteresis between cooling (blue) and heating (red) at 10 kOe. (d) The magnetic field dependence of the transition temperature determined by the inflection points of magnetization curves. The dashed red line shows the linear fit of the data.

Full size image

Consistent with the increase in ferrimagnetic transition temperature under magnetic fields, specific heat-capacity curve measured under magnetic fields also shifts to a higher temperature with the linear field coefficient of 0.102 ± 0.001 K kOe−1, which is consistent with the value obtained in the magnetization measurement (Fig. 3a and Figure S2 in the Supporting information). At 50 kOe the specific heat capacity peak shifts by about 5 K and shows little overlap (16.5%) with that at 0 kOe. The result demonstrates that 83.5% of the whole latent heat can be utilized through the MCE at 50 kOe. Because the obtained specific heat capacity measured with a relaxation method by PPMS often underestimates the actual latent heat for a first-order transition38, we then evaluated the magnetic entropy change, \(\Delta {S}_{M}\), from isothermal magnetizations as a function of applied magnetic fields. From the Maxwell relation

$${\left(\frac{\partial {S}_{M}}{\partial H}\right)}_{T}={\mu }_{0}{\left(\frac{\partial M}{\partial T}\right)}_{H},$$
(1)

the magnetic entropy is described as

Figure 3
figure 3

(a) Specific heat-capacity curves of BiCu3Cr4O12 measured under applied fields from 0 to 50 kOe. (b) Isothermal magnetization as a function of applied field for BiCu3Cr4O12 between 170 and 210 K. (c) Isothermal entropy changes for BiCu3Cr4O12 obtained from the magnetization changes measured under magnetic fields from 0 to 50 kOe. Yellow cross marks with a line represents the entropy changes estimated by the Clausius–Clapeyron equation using the magnetization data. (d) Calculated adiabatic temperature change induced by applying a magnetic field of 50 kOe.

Full size image
$$\Delta {S}_{M}={\mu }_{0}{\int }_{0}^{H}{\left(\frac{\partial M}{\partial T}\right)}_{H}\mathrm{d}H.$$
(2)

With the isothermal magnetization measurement results from 170 to 210 K presented in Fig. 3b, the magnetic entropy change \(\Delta {S}_{M}\) is thus estimated by the following formula:

$$\Delta {S}_{M}\left(\frac{2T+\Delta T}{2}\right)={\mu }_{0}{\int }_{0}^{H}\left\{\frac{M\left(T+\Delta T\right)-M\left(T\right)}{\Delta T}\right\}\mathrm{d}H,$$
(3)

where \(\Delta T\) is the difference in temperature between which the isothermal magnetization data are taken (1 or 2 K in the present experiments) (see Fig. 3b,c). The resultant \(\Delta {S}_{M}\) as a function of temperature is displayed in Fig. 3c. The maximum magnetic entropy change under 50 kOe reaches 22.6 J K−1 kg−1. Given that 83.5% of the transition entropy is released by the MCE at 50 kOe as mentioned above, the whole entropy change through the MCE should reach 27.1 J K−1 kg−1, which is comparable to that observed in DSC at zero field. This implies that almost all the latent heat originates from the magnetic entropy change and this large latent heat can be utilized through the MCE.

The magnetic entropy change can also be evaluated from the Clausius–Clapeyron equation:

$$\Delta {S}_{M}=-\Delta M{\left(\frac{\Delta {T}_{C}}{\Delta H}\right)}^{-1},$$
(4)

where \(\Delta M\) is the difference between the magnetizations of the two phases and \(\Delta {T}_{C}/\Delta H\) is the magnetic field dependence of the transition temperature39,40. The obtained \(\Delta {S}_{M}\) at 50 kOe with \(\Delta {T}_{C}/\Delta H\) determined by the inflection point in the magnetization curves (Fig. 2d) is also shown in Fig. 3c. It is noted that the magnetic entropy changes obtained from an indirect method with Maxwell relation are completely consistent with the results obtained from the Clausius–Clapeyron equation. The result is also consistent with the large latent heat observed in the present compound being primarily derived from the spin degree of freedom. The refrigerant capacity (RC), which is obtained by integrating \(\Delta {S}_{M}\), is 101.1 J kg−1 at 50 kOe. The adiabatic temperature change caused by the MCE at 50 kOe,

$${\Delta T}_{ad}\left(T\right)={\lceil{T\left(S\right)}_{50 \,\mathrm{kOe}}-{T\left(S\right)}_{0 \,\mathrm{kOe}}\rceil}_{S}$$
(5)

is shown in Fig. 3d and the maximum adiabatic temperature change reaches 3.9 K at 189 K. Although magnetic hysteresis in a cycle of magnetic field change is not significant in the present compound (Figure S3a in the Supporting information), it causes hysteresis loss near the phase transition temperature41,42. The loss is estimated from the area of field magnetization loop as shown in Figure S3b in the Supporting information, and the maximum value is about 7 J kg−1 at 191 K and 50 kOe.

Importantly, the large latent heat produced by the first-order charge disproportionation transition in BiCu3Cr4O12 can also be utilized through a BCE by applying hydrostatic pressure, as in the case of charge-transferred NdCu3Fe4O1237. Figure 4a shows the calorimetric curves obtained by differential thermal analysis (DTA) measurements at various pressures. Note that the exothermic peak shifts to a lower temperature under a pressure with the pressure coefficient of − 1.12 ± 0.02 K kbar−1 and − 1.36 ± 0.10 K kbar−1 respectively in cooling and heating as shown in Fig. 4b. The isothermal entropy changes produced by applying pressure are estimated by the following equation,

Figure 4
figure 4

(a) Heat flow curves divided by cooling rates in BiCu3Cr4O12 measured under applied pressure from 0 to 4.9 kbar. Heat flow curves on heating are also shown in the lower panel. (b) Pressure dependences of peak temperature of the heat flow. The dashed lines show the linear fits of the data. (c) Corresponding entropies as a function of temperature under various applied pressures. Entropy is calculated using the equation described in the method section. The entropies on cooling are relative to the value at 200 K. (d) Calculated adiabatic temperature change induced by applying pressure of 4.9 kbar. (e) Isothermal entropy changes in both cooling and heating at 4.9 kbar. The shaded area represents a region of reversible entropy change.

Full size image
$${\Delta S}_{p}=S\left(T,p\right)-S\left(T,0\right).$$
(6)

The results are shown in Fig. 4c, and the maximum entropy change is found to reach 27.2 J K−1 kg−1 at 4.9 kbar on cooling. The result clearly demonstrates that the large entropy change observed in the DSC measurement is utilized through the BCE at 4.9 kbar. The corresponding adiabatic temperature change at 4.9 kbar,

$${\Delta T}_{ad}\left(T\right)={\lceil{T\left(S\right)}_{4.9\,\mathrm{ kbar}}-{T\left(S\right)}_{\mathrm{ambient}}\rceil}_{S}$$
(7)

is seen in Fig. 4d, and the maximum value reached 4.8 K at 189 K. The RC value at 4.9 kbar on cooling is 140 kg−1. The reversible temperature range, which is determined from the DTA measurements on cooling and heating under pressure, is also shown in Fig. 4e. The BCE is reversible between 185 and 189 K, and a higher pressure than 4.9 kbar is necessary for utilizing the full entropy change in BCE by the phase transition.

The present BiCu3Cr4O12 exhibits both the MCE and the BCE. The large latent heat produced by the charge disproportionation transition can be utilized by applying both magnetic fields and hydrostatic pressure. An important point in the compound is that the phase transition can be tuned by applying fields in multiple ways while keeping the first-order sharp behaviors. Therefore, the large latent heat produced by the phase transition is also utilized in multiple ways. Although we presented the experimental results of MCE and BCE separately, we believe that the observed large entropy changes can be utilized by applying both magnetic fields and pressure simultaneously and thus the compound is multicaloric, because the charge, the spins, and the lattice are strongly coupled in the present BiCu3Cr4O12. Actually, as shown in Fig. 5, the phase transition temperature can be tuned by applying both magnetic fields and pressure simultaneously. As indicated by the linear field (magnetic field and pressure) dependences of the phase transition temperature, a planar surface separates the charge-uniform and charge-disproportionated phases (Fig. 5c). This multicaloric feature naturally provides us access to a wider range of control parameters, such that the phase transition where the entropy changes significantly can become accessible with fields in a broader window of temperature. An applied pressure to achieve a certain caloric effect, for example, can be tuned under a magnetic field. An effective magnetic field for utilizing the latent heat with the MCE can be controlled by applying pressure. In principle, it should be possible to eliminate the hysteresis as seen in the Fe49Ph51 alloy43.

Figure 5
figure 5

(a) Temperature dependent magnetization for BiCu3Cr4O12 measured under a 10 kOe magnetic field and various pressure. (b) Variation in phase transition temperature Tt by applying both magnetic fields and pressure. (c) 3D plot of phase transition temperature. The obtained planar surface represents the change of phase transition temperature by applying both magnetic fields and pressure.

Full size image

The phase transition in BiCu3Cr4O12 is primarily caused by the charge instability of the high and mixed valence state of Cr3.75+, which induces the charge disproportionation transition26. An important point is that the magnetic states of constituent cations also change according to the change in the charge states. Each magnetic moment abruptly appears and simultaneously order themselves at the charge transition temperature, and the behaver is completely different from the order–disorder-type transition of the magnetic moments in most of the magnetic materials. This unusual first-order magnetic transition yields the large magnetic entropy change. The magnetic entropies are thus significantly changed by the charge transition. Importantly, charge, spin, and lattice degrees of freedom in BiCu3Cr4O12 are strongly coupled, and as a result, the charge transition is tuned by applying external fields like agnetic fields and pressure. Therefore, the large magnetic entropy change produced by the charge transition is controlled by different kinds of applied fields and can be utilized through the caloric effects. The charge transition in the charge–spin–lattice coupled system gives rise to the present large multiple caloric effects.

Conclusions

We discovered that the quadruple perovskite structure oxide BiCu3Cr4O12 showed large multiple caloric effects; that is, it showed both magnetocaloric and barocaloric effects produced by the charge transition. The large latent heat of 5.23 kJ kg−1 and the corresponding entropy change of 28.2 J K−1 kg−1 are utilized by applying both magnetic fields and pressure. The multiple caloric effects are primarily driven by the magnetic entropy change in the unusual first-order magnetic transition accompanying the charge disproportionation transition of the mixed valence Cr3.75+. The charge, the spins, and the lattice are strongly correlated in the compound, and thus the phase transition caused by the electronic instability is tuned by multiple factors. The corresponding entropy changes are therefore able to be utilized through the multiple caloric effects. With this material, adiabatic temperature changes reach 3.9 K for the 50 kOe magnetic field and 5.4 K for the 4.9 kbar pressure, and thus highly efficient thermal controls are achieved in multiple ways. The present results demonstrate that a phase transition in charge–spin–lattice coupled system can be utilized as thermal control through multiple caloric effects. Our results open a new avenue to develop novel caloric materials.

Methods

A polycrystalline BiCu3Cr4O12 sample was prepared by solid-state reaction under a high-pressure and high-temperature condition. The sample was synthesized from the stoichiometric mixture of Bi2O3, CuO, CrO2, and Cr2O3. The mixture was pressed at 9 GPa and heated at 1273 K for 30 min and then cooled to room temperature. The pressure was slowly released after the heat treatment. The obtained sample was confirmed to be a single phase by synchrotron X-ray diffraction (SXRD). The results of structure analysis are given in Supporting information. The structure parameters were refined by Rietveld analysis using the RIETAN-FP program44. The crystal structure figures were drawn using the VESTA software45.

The magnetization data of the powder samples were collected with a SQUID magnetometer (Quantum Design MPMS XL) between 10 and 300 K under magnetic fields from 1 to 50 kOe. Isothermal magnetization data were collected from 0 to 50 kOe between 170 and 210 K.

Differential scanning calorimetry (NETZSCH DSC3500) was carried out at heating and cooling rates of 10 K min−1. The heat flow curves were obtained by subtracting the base change. The latent heat \(Q\) and the entropy change \(\Delta S\) associated with the transition were calculated as \({{Q}}={\int }_{{{T}}_{{b}}}^{{{T}}_{{a}}}{\mathrm{d}}{\dot{Q}}/{\dot{T}}{\mathrm{d}}{T}\) and \(\Delta {S}={\int }_{{{T}}_{{b}}}^{{{T}}_{{a}}}\left\{(-{\mathrm{d}}{\dot{Q}}/{\dot{T}})/{T}\right\}{\mathrm{d}}{T}\), where \({\mathrm{d}}{\dot{Q}}\) is the heat flow and \(\dot{T}\) is the cooling or heating rate. The heat-capacity measurements under various magnetic fields were performed by a commercial calorimeter (Quantum Design PPMS) using the heat relaxation method in the heating process. A pellet sample was used and was fixed on the sample holder by Apiezon N grease. RC in MCE was estimated by integrating \(\Delta {S}_{M}\) between the temperatures at the half maximum of the peak in \(\Delta {S}_{M}\).

Differential thermal analysis (DTA) measurements were carried out by using a pressure cylinder made of Cu–Be. The details of the equipment and the setup are described in the reference46. A T-type thermocouple was adhered with varnish to each sample and the CuO reference pellet. The DTA cell with Daphne7373 pressure medium was inserted in the pressure cylinder. Hydrostatic pressure was applied by a hydraulic cylinder via a piston. The sample temperature was controlled using liquid nitrogen. The heat flow (divided by cooling rate) curves were obtained with the DTA signal δT as dq/dT =  − AδT\(/\dot{T}\). Because the proportional constant A scarcely changed during measurements with the same setup conditions under pressure, the A value was determined from the heat flow \(\dot{Q}\) measured by DSC under an ambient condition. The entropy was evaluated as \(S(T,p)={\int }_{{T}_{b}}^{{T}_{a}}\left\{(-A\delta T(p)/\dot{T})/T\right\}\mathrm{d}T\). The isothermal entropy change \({\Delta S}_{p}\) at each pressure was calculated as \({\Delta S}_{p}=S\left(T,p\right)-S(T,0)\). The reversible temperature range was determined from the DTA measurements on cooling and heating under pressure. RC in BCE was estimated by integrating \(\Delta S\) between the cold and hot reservoir temperatures, where \(\Delta S\) was a half value of the maximum.