Introduction

The infectious disease (COVID-19) caused by the coronavirus (SARS-CoV-2) is spreading to a large number of individuals1,2,3. According to the WHO report, many people died by COVID-194. It is an urgent worldwide issue to break the chain of COVID-19 infection. Two major protection approaches are known: prevention and isolation. The former is a prepared protection for a person, such as masks and hand-washing. Vaccination has been thought to be the most effective method of prevention5,6. In contrast, the isolation (or segregation) means the cut-off of contact between infected and non-infected people. An example is quarantine to put an infected person into hospital. Another example is lockdown: mobilities of people are prohibited7,8. Very recently, vaccination is found to be the most effective method for COVID-196,9. However, in England, Republic of Chile and State of Arizona, the infection is widespread, even though the vaccination rate is above 40%4,6. Moreover, much time is still needed for vaccines to become widespread. Various types of infection control measures will be necessary.

We apply agent-based model (ABM) used in complex systems10,11,12,13,14,15,16,17. For infectious diseases, ABM is one of fundamental tools18,19,20. The epidemic spreading on lattices and networks have been studied by many authors20,21,22,23,24,25. In the present article, we explore the effect of mobility (random walk) on the isolation of infectious people. Infected people are divided into two groups, quarantined (Q) and non-quarantined (N) agents. The former can be detected by inspections; e.g. PCR test.

A certain proportion of infected people become severe, such as pneumonia3,26. In many countries, hospital beds are very crowded. To suppress the epidemic spreading, it should be important to quarantine the infected individuals. From the early stage of the epidemic, the importance of asymptomatic infection has been pointed out because the asymptomatic patient also behaves as a cryptic source of spreading infection27. Thus, a large number of people have being inspected by PCR test in the world. However, the application of PCR test for no symptom person has been restricted in Japan because the medical diagnostic PCR test resources were too poor to promote the test in the early period of the epidemic. Major academic societies in Japan claimed that PCR testing was basically not recommended for asymptomatic or mildly ill individuals28. Such claims raise some problems. (1) Is it okay to leave the infected person unchecked? (2) Does the number of Q-agents (PCR-positive) always increase with the number of tests? It has been reported for COVID-19 that most infected people have mild or no symptoms3,29. Because such people behave like uninfected people, they have considerably high infectivity30,31,32,33. This may be a distinct feature of COVID-19 never observed for the previous coronaviruses, SARS and MERS. We carry out simulations of random walk to report N-agents play a major role for epidemic spreading.

So far, various epidemic models have been presented for analyzing an epidemic spread34,35,36,37. In most cases, the epidemic of influenza and other infectious diseases has been theoretically explained by SIR model38,39,40,41 that considers susceptible (S), infected (I), and recovered (R) people. Interactions are represented as follows:

$${\text{S}} + {\text{I}} \to {\text{I}} + {\text{I}}\;\;\;\;\;\;\left( {{\text{rate}}:\beta } \right)$$
(1a)
$${\text{I}} \to {\text{R}}\;\;\;\;\;\;\left( {{\text{rate}}:\gamma } \right)$$
(1b)

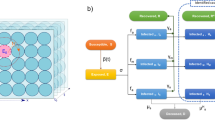
where β and γ represent infection and recovery rates, respectively. The spatial and network versions of SIR model is studied extensively in various fields42,43,44,45,46. In the present paper, we modify the SIR model as shown in Fig. 1a. Infected people are divided into quarantined (Q) and non-quarantined (N) agents. Similarly, the recovered (plus dead) people are also divided into \({\mathrm{R}}_{\mathrm{Q}}\) and \({\mathrm{R}}_{\mathrm{N}}\). Such a division may give us valuable information, because only the population size of Q (or \({\mathrm{R}}_{\mathrm{Q}}\)) is announced in public. It is important to know the behavior of N.

Figure 1
figure 1

Model and population dynamics. (a) Schematic illustrations of infection model. (b) Predictions of mean-field theory (MFT) which agree with the simulation results of global interaction. In the present article, we put \({\rho }_{0}=0.2\) and the initial condition is set as follows: (S, N) = (0.792, 0.008) and the other densities are zero at t = 0. Values of parameters in all figures are listed in Table S1.

Full size image

Method

We study epidemic spreading on a lattice. Each cell is either empty (O) or occupied by an individual (agent). The agent takes one of five states: S, Q, N, \({\mathrm{R}}_{\mathrm{Q}}\) and \({\mathrm{R}}_{\mathrm{N}}\). Symbols and parameters are listed in Table 1. Interactions are represented as follows:

$${\text{S}} + {\text{N}} \to i + {\text{N}}\;\;\;\;\;\;\;({\text{rate}}:\beta_{{\text{N}}} )$$
(2a)
$${\text{S}} + {\text{Q}} \to i + {\text{Q}}\;\;\;\;\;\;({\text{rate}}:\beta_{{\text{Q}}} )$$
(2b)
$${\text{N}} \to {\text{R}}_{{\text{N}}} \;\;\;\;\;({\text{rate}}:\gamma_{{\text{N}}} )$$
(2c)
$${\text{Q}} \to {\text{R}}_{{\text{Q}}} \;\;\;\;\;({\text{rate}}:\gamma_{{\text{Q}}} )$$
(2d)

where \(i\) denotes an infected agent (\(i=\mathrm{N},\mathrm{ Q}\)). The parameters \({\beta }_{\mathrm{i}}\) and \({\gamma }_{\mathrm{i}}\) denotes the infection and recovery rates of \(i\), respectively. We introduce "quarantine ratio" \(q\) which denotes the ratio of Q among all infected agents (see Fig. 1a). If \(q=1\), every infected agent is confirmed to be infected by testing (e.g. PCR test). In contrast, if \(q=0\), no infected agents are tested. We consider both \({\mathrm{R}}_{\mathrm{N}}\) and \({\mathrm{R}}_{\mathrm{Q}}\) have no infectivity. When the agent Q stays in hospital, \({\beta }_{\mathrm{Q}}\) takes a negligible value. However, when Q is waiting (or staying) at home, it is not negligible. In the present article, we assume \({\beta }_{\mathrm{N}}>{\beta }_{\mathrm{Q}}\) as discussed later.

Table 1 Descriptions of symbols and parameters.
Full size table

Simulations are carried out either by local or global interaction. Initially, few infected individuals are randomly positioned, and we put empty cells with density \({\rho }_{0}\); in this article we put \({\rho }_{0}=0.2\). Simulation for local interaction is performed as follows.

  1. (i)

    Infection processes (2a) and (2b): we randomly choose a single cell. If the cell is S and its nearest-neighbor site is occupied by N or Q, then S change to infected agent \(i\) with probability \({\beta }_{i}\). We put \(i\)=Q by probability \(q\), but \(i\)=N by probability \((1-q)\). Here, boundaries are periodic.

  2. (ii)

    Recovery and death processes (2c) and (2d): we randomly select one cell. If the site is N, it changes to \({\mathrm{R}}_{\mathrm{N}}\) with rate \({\gamma }_{\mathrm{N}}\). Similarly, if the selected site is Q, it becomes \({\mathrm{R}}_{\mathrm{Q}}\) with rate \({\gamma }_{\mathrm{Q}}\).

  3. (iii)

    Random walk: we randomly select two neighboring cells. If the first and second chosen cells are respectively the cell of agent \(j\) and empty cell (\(j=\mathrm{S},\mathrm{N},\mathrm{Q},{\mathrm{R}}_{\mathrm{N}},{\mathrm{R}}_{\mathrm{Q}}\)), then both cells are exchanged with migration rate \({m}_{j}\). Hence, the agent \(j\) moves into the empty cell with rate \({m}_{j}\). Note that we have \({m}_{j}=2\), when only step (iii) is repeated twice.

In the simulation, the unit of time \(t\) is measured by Monte Carlo step (MCS)14,15. Namely \(t\) increases by 1 MCS, when steps (i)–(iii) are repeated by 104 times; note 104 is the total cell number of lattice. The simulation is continued until the system reaches a steady state. In the case of global interaction, infection process (i) occurs between any pair of cells. We can skip the random walk in the simulation of global interaction, because all agents randomly distribute.

The well-mixed population for epidemic model is given by mean-field theory (MFT):

$$dS/dt=-{\beta }_{N}SN-{\beta }_{\mathrm{Q}}SQ$$
(3a)
$$dN/dt=(1-q){\beta }_{\mathrm{N}}SN+(1-q){\beta }_{\mathrm{Q}}SQ-{\gamma }_{N}N$$
(3b)
$$\mathrm{dQ}/\mathrm{dt}=q{\beta }_{\mathrm{N}}SN+q{\beta }_{\mathrm{Q}}SQ-{\gamma }_{\mathrm{Q}}Q$$
(3c)
$$d{R}_{N}/dt={\gamma }_{\mathrm{N}}N$$
(3d)
$$d{R}_{Q}/dt={\gamma }_{\mathrm{Q}}Q$$
(3e)

Here the densities of S, N, Q, \({\mathrm{R}}_{\mathrm{N}}\) and \({\mathrm{R}}_{\mathrm{Q}}\) are shown in their italics. The total densities of agents are given by \((1-{\rho }_{0})\), where \({\rho }_{0}\) is the density of empty cell. If \(q=0\) and \({\beta }_{\mathrm{Q}}=0\), then Eqs. (3a–3e) agrees with those for SIR model. The threshold phenomenon is well known for SIR model34,38. When \({\beta }_{N}/{\gamma }_{N}\) > 1/S(0), the disease spreads. Similarly, if \(q=1\) and \({\beta }_{\mathrm{N}}=0\), the disease spreads for \({\beta }_{\mathrm{Q}}/{\gamma }_{\mathrm{Q}}\) > 1/S(0).

Results

Results for global interaction

The simulation results of global interaction agree with those predicted by MFT. This is because the global interaction corresponds to the assumption of well-mixed population. First, the numerical calculation for global interaction is reported. In Fig. 1b, a typical population dynamics for MFT are displayed. Model parameters used in all figures are listed in Table S1 (see Supplementary file). At the final equilibrium (\(t\to \infty\)), both densities N \((\infty )\) and Q \((\infty )\) become zero, but \({R}_{N}(\infty )\) and \({R}_{Q}(\infty )\) take constant values. Namely, agents N and Q always change to \({\mathrm{R}}_{\mathrm{N}}\) and \({\mathrm{R}}_{\mathrm{Q}}\), respectively. Hereafter, we will call \({R}_{N}\left(\infty \right)+{R}_{Q}\left(\infty \right)\) "total infection" and \({R}_{Q}(\infty )\) "apparent infection". The former accurately indicates the degree of infection, but its measurement may be impossible. Realistically, only the latter index is announced in public.

In Fig. 2, both total and apparent infections are depicted against the ratio \(q\). We find a threshold phenomenon as observed for SIR model34,38. When the ratio \({\beta }_{N}/{\gamma }_{N}\) takes a small value, the disease never spreads. In contrast, when \({\beta }_{\mathrm{N}}/{\gamma }_{\mathrm{N}}\) takes a large value, the infection can spread. The threshold of \({\beta }_{N}/{\gamma }_{N}\) becomes small, when \({\beta }_{\mathrm{Q}}/{\gamma }_{\mathrm{Q}}\) takes a large value. We also find that the apparent infection (\({R}_{Q}\)) takes a maximum value at \(q={q}_{MAX}\), where \({0<q}_{MAX}<1\). When \({q<q}_{MAX}\), the total number of Q increases with increasing q. On the contrary, when \({q>q}_{MAX}\), it decreases in spite of the increase of q. The value of \({q}_{MAX}\) is found to be increased with the increase of \({\beta }_{N}/{\gamma }_{N}\). It should be emphasized that the total infection monotonically decreases with increasing q. Hence, isolating the infected agents is effective to suppress the infection. In this paper, we put \({\gamma }_{N}{=\gamma }_{\mathrm{Q}}\); this is because both ratios \({\beta }_{N}/{\gamma }_{N}\) and \({\beta }_{\mathrm{Q}}/{\gamma }_{\mathrm{Q}}\) are found to be more important parameters than \({\gamma }_{N}\) and \({\gamma }_{\mathrm{Q}}\). Numerical calculation reveals that both total and apparent infections increase with the increase of either \({\beta }_{N}/{\gamma }_{N}\) or \({\beta }_{\mathrm{Q}}/{\gamma }_{\mathrm{Q}}\).

Figure 2
figure 2

Results of final densities for MFT. The total infection [\({R}_{N}\left(\infty \right)+{R}_{Q}\left(\infty \right)\)] and apparent infection [\({R}_{Q}\left(\infty \right)\)] are plotted against quarantine ratio (q). We fix \({\gamma }_{\mathrm{N}}={\gamma }_{\mathrm{Q}}=0.2\), \({\beta }_{\mathrm{Q}}=0.1\). (a) \({\beta }_{\mathrm{N}}=0.8\), (b) \({\beta }_{\mathrm{N}}=0.4\) and (c) \({\beta }_{\mathrm{N}}=0.1\).

Full size image

Results for random-walk simulation

Simulation results for local interaction are described. To know the relation between local and global simulations, we first assume the special case that the migration rate (\({m}_{j})\) of agent \(j\) takes the same value for all agents (\({m}_{j}=m\) for \(j=\mathrm{S},\mathrm{N},\mathrm{Q},{\mathrm{R}}_{\mathrm{N}},{\mathrm{R}}_{\mathrm{Q}}\)). In Fig. 3, the effect of random walk is illustrated; in (a) and (b), the final densities are plotted against the migration rate (\(m\)). It is found that both total and apparent infections increase with \(m\). The infection hardly spreads for \(m=0\), while it widely spreads for a large value of \(m\). Especially when \(m\) is sufficiently large, the results of local interaction approach those predicted by MFT.

Figure 3
figure 3

Results of random-walk simulation at the final stage (\(t=1000\)). All people (agents) randomly migrate with the same migration rate (m) on a lattice (\(100\times 100\)). In (a) and (b), the total infection [\({R}_{N}\left(\infty \right)+{R}_{Q}\left(\infty \right)\)] and apparent infection [\({R}_{Q}\left(\infty \right)\)] are plotted against m, respectively. The straight lines indicate the results of MFT which agree with those of global interaction.

Full size image

Realistically, both agents Q and \({\mathrm{R}}_{\mathrm{Q}}\) never move. Next, we consider the case that three agents (S, N, \({\mathrm{R}}_{\mathrm{N}}\)) can move; we fix \({m}_{\mathrm{S}}=2\), and change the migration rates of N and \({\mathrm{R}}_{\mathrm{N}}\) with the same rate (\({m}_{k}={m}_{\mathrm{N}}\) for \(k=\) \({\mathrm{R}}_{\mathrm{N}}\)). In Fig. 4, the final densities are plotted against \({m}_{\mathrm{N}}\), where (a) \(\left(q,{\beta }_{N},{\beta }_{Q}\right)=\left(0.2, 0.3, 0.1\right)\), (b) \((q,{\beta }_{N},{\beta }_{Q})=(0.2, 0.1, 0.3)\) and (c) \((q,{\beta }_{N},{\beta }_{Q})=(0.8, 0.3, 0.1)\). Both values \(q=0.2\) and \(q=0.8\) represent the cases that the inspection is insufficient and sufficient, respectively. Figure 4b represents a symmetrical case to Fig. 4a: \({\beta }_{N}<{\beta }_{Q}\). It is found from Fig. 4a that both total infection (\({R}_{N}+{R}_{Q}\)) and apparent infection (\({R}_{Q}\)) rapidly increase with the increase of \({m}_{\mathrm{N}}\). When N and \({\mathrm{R}}_{\mathrm{N}}\) sufficiently move around, the simulation results of random walk agree with those predicted by MFT (well-mixed population). The infection rapidly spreads. In contrast, Fig. 4b shows different behavior. For small values of \({\beta }_{\mathrm{N}}\), both total and apparent infections hardly increase in spite of the increase of \({m}_{\mathrm{N}}\); the infection becomes very difficult to spread. Similarly, when the inspection is sufficient (\(q=0.8\)), the infection can be suppressed.

Figure 4
figure 4

Serious effect of non-quarantined agents (N). Both [\({R}_{N}\left(\infty \right)+{R}_{Q}\left(\infty \right)\)] and \({R}_{Q}\left(\infty \right)\) are plotted against \({m}_{\mathrm{N}}\). Uninfected agent (S) can move with \({m}_{\mathrm{S}}=2\). The horizontal axis means the migration rate (\({m}_{\mathrm{N}})\) of N, where both N and \({\mathrm{R}}_{\mathrm{N}}\) move with the same rate. In contrast, the other agents (Q and \({\mathrm{R}}_{\mathrm{Q}}\)) never move: \({m}_{k}=0\) for \(k=\mathrm{Q},{\mathrm{R}}_{\mathrm{Q}}\).

Full size image

In Fig. 5a and b, the total (\({R}_{N}+{R}_{Q}\)) and apparent (\({R}_{Q}\)) infections are plotted against q, respectively. Here, three agents (\(\mathrm{S},\mathrm{N},{\mathrm{R}}_{\mathrm{N}}\)) can move: \({m}_{j}=10\) for \(j=\mathrm{S},\mathrm{N},{\mathrm{R}}_{\mathrm{N}}\) but \({m}_{k}=0\) for \(k=\mathrm{Q},{\mathrm{R}}_{\mathrm{Q}}\). As predicted by MFT, the total infection monotonically decreases with the increase of q, but the apparent infection has the maximum at \(q={q}_{MAX}\). The value of \({q}_{MAX}\) for local interaction is found to be smaller, compared to the prediction of MFT. In Fig. 5c and d, both total and apparent infections are also plotted against \({\beta }_{\mathrm{N}}\), respectively. These figures display the phase transition. When \({\beta }_{\mathrm{N}}\) takes a small value, the infection never spreads. With the increase of \({\beta }_{\mathrm{N}}\), the infected people suddenly increase. In Fig. 6, typical spatial distributions are displayed, where no agent moves in (a), only S moves in (b), and three agents (S, \(\mathrm{N}, {\mathrm{R}}_{\mathrm{N}}\)) move in (c). For the sake of comparison, the result of global simulation (random distribution) is displayed in Fig. 6d. In the cases of Fig. 6a and b, the infection is suppressed; many cells are occupied by blue (S). The infected agents form clusters and stay inside localized spots. However, in Fig. 6c and d, the infection widely spread. It is therefore important to stop the movement of N agents.

Figure 5
figure 5

Comparison between local and global interactions. In the former, random-walk simulations are carried out; three agents (S, \(\mathrm{N}, {\mathrm{R}}_{\mathrm{N}}\)) can move with the same rate \({m}_{j}=10\) for \(j=\mathrm{S}, \mathrm{N}, {\mathrm{R}}_{\mathrm{N}}\) (\({m}_{k}=0\) for \(k=\mathrm{Q},{\mathrm{R}}_{\mathrm{Q}}\)). In (a) and (b), both [\({R}_{N}\left(\infty \right)+{R}_{Q}\left(\infty \right)\)] and \({R}_{Q}\left(\infty \right)\) are plotted against the quarantine ratio (q), respectively. In (c) and (d), the same as (a) and (b) are plotted, but the horizontal axis denotes the infection rate (\({\beta }_{\mathrm{N}}\)) of N.

Full size image
Figure 6
figure 6

Typical spatial patterns at the final stage (\(t=1500\)). (a) Interactions occur between adjacent cells (local interaction). Nobody can move around ("lockdown"). (b) Local interaction. Only agent S can move around (\({m}_{\mathrm{S}}=10\), but \({m}_{j}=0\) for \(j\ne \mathrm{S}\)). (c)Local interaction. Mobile agents are limited to S, N and \({\mathrm{R}}_{\mathrm{N}}\); namely \({m}_{j}=10\) for \(j=\mathrm{S},\mathrm{N},{\mathrm{R}}_{\mathrm{N}}\) but \({m}_{k}=0\) for \(k=\mathrm{Q},{\mathrm{R}}_{\mathrm{Q}}\)). (d) Global interaction (random distribution). Each site is either empty (white) or occupied by S (blue), RN (green) or RQ (black).

Full size image

Discussion

The coronavirus SARS-CoV-2 has distinct features never seen for previous coronaviruses, such as SARS and MERS. In the case of SARS-CoV-2, many infected people have mild or asymptomatic symptoms, but they may have considerably high infectivity27,30,31,32,33. We demonstrate the serious role of infected people who are not quarantined (N). To this end, we have modified SIR model; infected individual (I) is divided into two groups (N and Q). Similarly, recovered individual (R) is divided into \({\mathrm{R}}_{\mathrm{N}}\) and \({\mathrm{R}}_{\mathrm{Q}}\) to distinguish the total and apparent infections. Model (2) resembles SIQR model24,43,44. In the latter case, infected agent (I) always transitions to Q with a constant probability (per unit time). For this reason, N cannot be defined well. However, in model (2), we assume the transition occurs only in the early stages of infection. Those who did not transition to Q are defined by N agents; in simple terms, a person who is infected but not tested is an agent N.

The setting of parameter values is discussed. If the value of \({\beta }_{N}/{\gamma }_{N}\) or \({\beta }_{Q}/{\gamma }_{Q}\) is sufficiently high, then the infection easily spreads. In the present paper, the parameters are set based on the following facts: (i) COVID-19 has been suppressed due to lockdown and other regulation of people’s behavior. (ii) Once unlocked, the infection spreads again (e.g. USA and Australia)4. In our model, the disease disappears when all people stop moving, but the infection spreads when people move frequently (see Fig. 3). Moreover, we assume \({\beta }_{\mathrm{N}}>{\beta }_{\mathrm{Q}}\) for the following reasons. Asymptomatic or mildly infected individuals tend to become agent N. On the other hand, those with severe disease may become agent Q. Since agent Q is quarantined, its infectivity (\({\beta }_{\mathrm{Q}}\)) may be low. In contrast, the infectivity (\({\beta }_{\mathrm{N}}\)) of N may be higher than \({\beta }_{\mathrm{Q}}\). This is because the agent N looks like uninfected agent (S); nevertheless, the value of \({\beta }_{N}/{\gamma }_{N}\) may considerably high27,30,31,32,33. Provided that \({\beta }_{\mathrm{N}}\) takes a small value, the infection hardly spreads as shown in Fig. 4b.

Random-walk simulation reveals that both total [\({R}_{N}\left(\infty \right)+{R}_{Q}\left(\infty \right)\)] and apparent [\({R}_{Q}(\infty )\)] infections rapidly increase with increasing the mobility (\({m}_{N}\)) of N (see Fig. 4). However, when the value of \({\beta }_{N}/{\gamma }_{N}\) is low, or when \(q\) takes a high value, the infection hardly spreads. Such a low value of \({\beta }_{N}/{\gamma }_{N}\) means the weak infectivity of N, and the high value of \(q\) denotes the small population size of N. Hence, non-quarantined infected individuals (N) play serious roles for epidemic spreading. It should be noted that the movement of \({\mathrm{R}}_{\mathrm{N}}\) never makes a large difference: if \({\mathrm{R}}_{\mathrm{N}}\) stops to move, Figs. 4, 5, and 6 are almost unchanged. Only when the movement of N is suppressed, the infection can be suppressed.

We discuss spatial pattern formations (see Fig. 6). As illustrated in Fig. 6a, the infection hardly spreads, because all people never move ("lockdown"). Most cells are blue (agent S). The infected agents (green and black) stay inside localized spots. Such a cluster formation may be a merit of lockdown: it is advantageous in taking measures against infectious diseases. Similarly, even when only agent S (non-infected person: blue cell) moves, the infection can be suppressed (see Fig. 6b). The following question arises: Why the infection is suppressed, despite the large number of non-infected persons intensely move. We consider this suppression comes from the spatial pattern formation. Both Fig. 6a and b have the similar distributions: the infected people form clusters. Since infected agents aggregate, the contact between infected and non-infected individuals is effectively decreased.

Conclusion

In the present article, we demonstrate the serious role of infected people who are not quarantined (N). Both mean-field theory and Monte Carlo simulation reveal the result schematically shown in Fig. S1 (see Supplementary file). The total infection monotonically decreases with the increase of quarantine ratio (q). In contrast, the apparent infection has the maximum at \({q=q}_{\mathrm{MAX}}\). For \({q>q}_{\mathrm{MAX}}\), the density of infected people decreases in spite of increasing q. Hence, it is important to promote the inspections; e.g. PCR test. Random-walk simulation reveals that the infection rapidly spreads with increasing the mobility of N. If the movement of N is suppressed, the infection can be suppressed. This conclusion is also confirmed by spatial distribution. Figure 6a indicates the spatial pattern of "lockdown"; infected people form clusters, because all people cannot move. Similar distribution is observed, if infected agents never move (see Fig. 6b). Since infected people aggregate, the infection hardly spreads. Hence, suppressing the movement of infected people (or expanding the tests) is as effective as lockdown. This result for COVID-19 should be unique property never seen for both SARS and MERS. It is therefore important to detect and quarantine the asymptomatic SARS-CoV-2 infected persons27,30,31,32,33.