Introduction

Gas and fluids interactions are an undeniable part of many industrial procedures, which plays some major roles in many industries like petrochemical1,2,3, oil and gas4,5,6,7,8,9, medicine10, food11,12, environment13,14, polymer15,16, etc. Among the common gaseous phases normally present in the mentioned environments, colorless odorless nitrogen (N2) is one of the most common gases included as the feed or product in many processes. On the other hand, the presence of this gas as the dominant part of atmosphere components makes it an important case to be investigated accurately. The oil and gas industry would not be an exception, and N2 applications are observed in many subsidiaries of this industry, from the upstream to downstream. As a clear example, N2 and its related treatments have been used since few decades ago because of its unique properties for enhanced oil recovery (EOR) operations17,18,19. Usually, carbon dioxide (CO2) or N2 gases are continuously injected into the oil reservoir for miscible/immiscible oil displacement. These gases are extracted back out with the recovered oil, recaptured, and reinjected along with new gas until as much oil as possible is produced20. Cost efficiency and higher feasibility make some advantages for this component (N2) in comparison with CO2 and methane (CH4)21,22. However, N2 has been commonly utilized in deep reservoirs as it needs a higher injection pressure to gain miscibility with the reservoir fluids than does CO220. Also, in the midstream, N2 is used in pipeline drying, which is an essential part of pipeline commissioning to prevent unwanted aerosols through contaminant displacing23. There are many significant instances of N2 usage in downstream, like nitrogen purging which is a technique to avoid unintentional reaction of hazardous gas and hydrocarbons through the oxygen reduction in the environments that is susceptible to explosion24 that is a similar technique which is used in nitrogen blanketing25 in hydrocarbon storage tanks. Crude oil is a complex mixture of hydrocarbons. Achieving reliable predictions for the thermodynamics and phase equilibrium data of N2/oil systems is complex and difficult. Alkanes are the major constituents of crude oil and most petroleum products. Therefore, in many studies, the behavior of alkanes and the desired gas like N2 is studied first, and the obtained information will be later generalized to crude oil.

Solubility is one of the most important thermodynamics values representing the value of a gas dissolution in a liquid at a specific pressure and temperature. While many analytical methods are used to calculate the solubilities of gases in liquids mainly through the equations of state (EOSs)26,27,28,29, the accuracy of their prediction, especially in some critical industrial applications, has been a serious challenge yet. Based on previous experiments, the solubility of N2 in hydrocarbons is positively affected by increasing pressure and temperature26,27,28. Furthermore, as the molecular weight rises, N2 solubility increases, as evidenced by laboratory experiments29. Properly estimating phase equilibrium data in binary systems containing N2 and a hydrocarbon is difficult. Because, based on the classification scheme of Van Konynenburg and Scott30,31, binary systems of a hydrocarbon and N2 are recognized as type III phase diagrams, except the binary system of N2 + CH4, which is recognized as a type I system30,31. Risk of energy waste and potential hazards exist in operations which use N2. As a result, solubility data is critical for predicting an appropriate quantity of N2 to use in this operation, and it can improve plant safety. Studies with heavy hydrocarbons are particularly challenging due to their complexity. Furthermore, the dangers of high-temperature and/or high-pressure conditions in industrial operations make the extensive experiments an undesirable option. As a result, modelling with experimental data would be an alternative.

Mainly, the strategies for the prediction of N2 solubility in hydrocarbon solvents or petroleum blends rely on experimental and semi-empirical models like EOSs, and are comparable to those utilized to estimate the solubility of other gasses like CH4, CO2, and hydrogen32,33,34,35,36,37. In compressed N2, the vapor-phase solubilities of n-Decane, ferf-butylbenzene, 2,2,5-trimethylhexane, and n-dodecane were determined by Davila et al.38 and the second virial cross coefficients (\(B_{12}\)) were computed using these data38. A static equilibrium cell was used by Tong et al.29 to test the solubilities of N2 in four n-paraffin hydrocarbons (Decane, Eicosane, Octacosane, and Hexatriacontane). The Soave–Redlich–Kwong (SRK) and Peng-Robinson (PR) EOS were applied to analyze the data. The results show a growing trend in N2 solubility with rising pressure, temperature, and n-paraffin chain length29. N2 solubilities in various naphthenic (trans-Decalin and cyclohexane) and aromatic (naphthalene, 1-methylnaphthalene, benzene, phenanthrene, pyrene) solvents were determined by Gao et al.26 using a static cell. When a single interaction parameter (\(C_{ij}\)) is employed in each binary system, the PR-EOS was demonstrated to fit the model26. Privat et al.39,40 used the PR EOS combined with the group contribution method, called the PPR78 model, for predicting phase equilibrium data of mixtures containing various hydrocarbons and N2. This model is able to predict temperature-dependent binary interaction parameters (kij). The mentioned model provided satisfying results with an overall deviation lower than 10%. They also mentioned that for the hydrocarbon + N2 systems (except CH4); kij is a decreasing function of temperature39,40. At low temperatures, Justo-Garcia et al.41 modeled vapor–liquid-liquid equilibria (VLE) for N2 and alkanes in three distinct ternary systems. The findings demonstrate that both SRK and PC-SAFT EOSs estimate the experimentally observed values with reasonable accuracy41. In another study, Justo-Garcia et al.42 used the SRK and PC-SAFT EOSs to model three-phase vapor–liquid–liquid equilibria for a combination of natural gas having high N2 content. The results revealed that the PC-SAFT EOS accurately predicts phase behavior, but the SRK EOS suggests a three-phase region that is larger than what was observed experimentally42. The Krichevsky–Ilinskaya equation was used by Zirrahi et al.27 to estimate the solubility of light solvents (CO2, N2, CH4, C2H6, and CO) in bitumens from five Alberta reservoirs. The gas phase is analyzed applying the PR-EOS. The suggested model is then validated using experimental data on light solvent solubility. The results demonstrated that the proposed model accurately reflects known solubility data in bitumen for light hydrocarbons (CH4 and C2H6) and non-hydrocarbon solvents (N2, CO2, and CO)27. Haghbakhsh et al.43 investigated the vapor–liquid equilibria of binary N2–hydrocarbon mixtures across an extensive range of temperature and pressure applying PR and ER EOSs. They introduced a new correlative mode for the proposed equations to improve accuracy, which was likely to be effective, improving accuracy by up to three times43. Thermo-physical characteristics of CO2 and N2/bitumen solutions were studied by Haddadnia et al.28. Furthermore, PR-EOS was used to describe the calculated solubility28. PC-SAFT and SRK EOSs were employed by Wu et al.44 to estimate gas solubilities in n-alkanes. The PC-SAFT EOS was found to be able to accurately predict an empirically observed linear connection between gas solubilities in n-alkanes and their carbon number. Despite its satisfactory accuracy for gas solubility in lighter n-alkanes, the SRK EOS typically produces significantly poorer results than the PC-SAFT EOS44. Tsuji et al.45 investigated N2 and oxygen gas solubilities in benzene, divinylbenzene, and styrene. For a particular isotherm, gas solubility in liquids had a linear pressure dependency and declined with rising temperature. Ultimately, PR-EOS was implemented to predict gas solubilities45. Aguilar-Cisneros et al.46 determined the solubility of N2, CO2, and CH4 in petroleum fluids using the PR-EOS in conjunction with various mixing rules in systems including bitumens, heavy oils, refinery cuts, and coal liquids. The universal and van der Waals mixing rules revealed satisfactory outcome between experimental data and predicted values, while the modified Huron-Vidal of order one mixing rule produced large discrepancies46.

During the last decade, alongside the developments of intelligent methods based on machine learning (ML) techniques, many attempts have been made to predict thermodynamic results with a higher accuracy based on reliable experimental data. Abdi-Khanghah et al.47 studied alkane solubility in supercritical CO2. Two kinds of artificial neural networks were used for their study: Radial basis function (RBF) and multi-layer perceptron (MLP) artificial neural network (ANN). The MLP-ANN outperformed the RBF-ANN in predicting n-alkane solubility in supercritical CO247. Songolzadeh et al.48 demonstrated that the PSO–LSSVM model is an effective technique for predicting n-alkane solubility in supercritical CO2 with high accuracy. The least-squares support vector machine (LSSVM) was employed, which was tuned using two different optimizing algorithms: particle swarm optimization (PSO) and cross-validation-assisted Simplex algorithm (CV-Simplex)48. Chakraborty et al.49 developed a set of data-driven models capable of predicting VLE for the binary systems of C10-N2 and C12-N2. In comparison to the VLE modeled using the PR-EOS, both models significantly improved the estimated value of binary mixture equilibrium pressure49. Mohammadi et al.50 implemented different ML models to predict hydrogen solubility in various pure hydrocarbons in wide pressure and temperature ranges and compared them with some of the common EOSs. Their results showed that using intelligent models shows more precise results than the common usage of EOSs in hydrogen solubility estimation50. To predict nitrogen solubility in unsaturated, cyclic and aromatic hydrocarbons, Mohammadi et al.51 employed a convolutional neural network (CNN) and the results showed that pressure is the most significant factor for nitrogen solubility in unsaturated hydrocarbons. In general, prediction based on EOSs semi-analytical methods has been the common way to estimate the N2 solubilities in alkanes. On the other hand, the mentioned method is case-specific and it is limited to some defined hydrocarbons with specific parameters for each EOS. Hence, using intelligent models like proper ML algorithms and reliable experimental data may lead to a model for predicting N2 solubility in normal alkanes with high accuracy and this helps to accelerate predictions.

In this study, we use a dataset containing 1982 experimental N2 solubility data points for 19 distinct normal alkanes gathered under various operating states. Models for estimating N2 solubility in normal alkanes are constructed using well-known ML algorithms namely k-nearest neighbor (k-NN) and random forest (RF), as well as innovative ML methods such as extreme gradient boosting (XGBoost), gradient boosting with categorical features support (CatBoost), and light gradient boosting machine (LightGBM). Furthermore, statistical parameters and graphical error assessments are used to verify the validity of the suggested models. Numerous N2 solubility systems are predicted by the methods proposed in this research and five EOSs, namely perturbed-chain statistical associating fluid theory (PC-SAFT), Redlich-Kwong (RK), Peng-Robinson (PR), Soave–Redlich–Kwong (SRK), and Zudkevitch-Joffee (ZJ). Eventually, the relevancy factor is utilized to assess the relative impact of input parameters on N2 solubility in normal alkanes.

Data collection

The modeling of N2 solubility in normal alkanes was performed using a large solubility databank containing 1982 data points collected from the literature29,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91. The properties of 19 normal alkanes (nC1 to nC36) utilized in this survey are presented in Table 1.

Table 1 The normal alkanes utilized in this survey.
Full size table

The inputs of the models were chosen to be temperature (K), pressure (MPa), and molecular weight (g/mol) of normal alkanes, whereas N2 solubility (in terms of mole fraction) was the desired output. The statistical details of the N2 solubility databank used for modeling are tabulated in Table 2. The validity, accuracy, and applicability of the model depend on the quantity and variety of N2 solubility data collected in different systems. The broad ranges of pressure (0.0212–69.12 MPa), temperature (91.21–703.4 K), and normal alkanes (nC1 to nC36) can lead to a reliable general model for estimating the solubilities of N2 in normal alkanes.

Table 2 The statistical information of the N2 solubility databank used in this paper.
Full size table

Models’ implementation

Algorithms’ selection

Due to recent advances in computation capacities and also the advent of new machine learning algorithms, there are many choices to use as algorithms for the problem under consideration. Because of the size of the dataset and small instance number and also based on the limited number of the features, some of the non-parametric ML models which mainly focus on the dataset and do not suffer from the small size of the dataset were noticed as the best choices in this case.

K-nearest neighbors (k-NN)

The k-NN method is an ML technique that is employed to solve both classification and regression problems. This supervised algorithm is widely used as a non-parametric technique for various applications92. In this algorithm, the k is the number of neighbors which are assigned to a new sample to predict the target based on its inheritance from these k samples that are closest to the new sample using a uniform weight assigning system or a specific distance function93. Distance function is a tool to allocate a weight to each of the k samples features to identify its contribution in final predicted value. Minkowski distance equation is the typical choice for the distance function. The general form of this equation is provided in Eq. (1), where X and Y are two samples feature sets. This function turns to Manhattan or Euclidean distance function in most of the cases by using the p = 1 or p = 2, respectively. Finding and selection of the optimal value of the k hyper-parameter is the most crucial stage in the training of this algorithm to achieve a satisfactory accuracy. Hence, the algorithms are run by a wide range of k value and the optimal case is revealed based on the comparison of statistical accuracy measurements among the explored cases.

$$\begin{aligned} D\left( {X,Y} \right) & = \left( {\mathop \sum \limits_{i = 1}^{n} \left| {x_{i} - y_{i} } \right|^{p} } \right)^{\frac{1}{p}} \\ X & = \left( {x_{1} ,x_{2} , \ldots ,x_{n} } \right) \;{\text{and}}\;Y = \left( {y_{1} ,y_{2} , \ldots , y_{n} } \right) \in {\mathbb{R}}^{n} \\ \end{aligned}$$
(1)

Random forest

Random forest is a bagging supervised learning technique for classification and regression using the ensemble learning approach based on CART (Classification and Regression Trees)94. This algorithm avoids high prediction variance, which is a common issue in the decision tree algorithm. Random forests have trees, which run parallelly. These trees do not have any interaction with each other during the forest construction. It works by training a large number of decision trees and then determining the class that is the mean prediction of the individual trees in regression cases. At each node, the number of attributes that may be divided is limited to a certain proportion of the total which is known as the hyperparameter. This guarantees that the ensemble model does not depend too strongly on any specific attribute and that all potentially predictive variables are considered equally. In any CART tree training, the random forest technique picks the training dataset Ti, randomly from the complete training set T, by replacement (i.e., bootstrapping sampling). The data that was not included in the random sampling technique is referred to as "out-of-bag" data. The random forest technique picks N features or input variables randomly from a set of M input independent factors (N < M) while building each CART tree. According to the randomly picked Ti and M characteristics, the best splitting for each CART tree is calculated. The final results of the regression are being determined via majority voting. To increase the estimation precision, the averaged prediction reduces the averaged squared error on the individual estimations produced from an individual CART tree. The resulting ensemble trees are designated as follows (Eq. 2):

$$\begin{gathered} \left\{ {\phi_{{T_{b} ,m}} \left| {b = 1, \ldots ,B} \right.} \right\} \hfill \\ \hat{Y} = \phi_{T,P} \left( X \right) = \frac{1}{B}\mathop \sum \limits_{b = 1}^{B} \phi_{{T_{b} ,m}} \left( X \right) \hfill \\ \end{gathered}$$
(2)

Extreme gradient boosting (XGBoost)

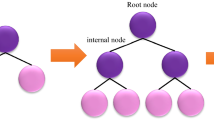
The fundamental concept behind a tree-based ensemble method is to use an ensemble of classification and regression trees (CARTs) to fit training data using a regularized objective function minimization. One of those other tree-based models is XGBoost, which is part of the gradient boosting decision tree framework (GBDT). To further explain the construction of the CART, each cart is made up of (I) a root node, (II) internal nodes, and (III) leaf nodes, as illustrated in Fig. 1. The root node, which represents the entire dataset, is split into internal nodes by the binary decision technique, whilst the leaf nodes reflect the final classifications. In gradient boosting, a sequence of basic CATRs are created simultaneously, with the weight of each individual CART being adjusted via the training process95.

Figure 1
figure 1

Level-by-level tree development in XGboost.

Full size image

An ensemble of n trees must be trained to predict the y for a specific dataset, m and n respectively show the count of features and instances.

$$\begin{aligned} \hat{y}_{i} = \sum\limits_{k = 1}^{N} {f_{k} \left( {X_{i} } \right),\;\;\,f_{k} \in f} \\ & With\;f= \left\{ {f(X) = \omega_{q(x)} } \right\},\;\left( {q:{\mathbb{R}}^{m} \to T,\;\omega \in {\mathbb{R}}^{T} } \right) \\ \end{aligned}$$
(3)

where the decision rule \(q\left( x \right)\) maps the example to the binary leaf index. \(n\) shows the regression trees space, \(f_{k}\) shows the kth independent tree, T represents the count of tree’s leaves, and w shows the leaf’s weight in Eqs. 3 and 4.

The minimization of the regularized objective function \(L\) is used to determine the ensemble of trees:

$$\begin{aligned} & L = \sum\limits_{i}^{n} {l(\hat{y}_{i} ,y_{i} ) + \sum\limits_{k}^{N} {\Omega \left( {f_{k} } \right)} } \\ & With\;\Omega (f) = \gamma T + \frac{1}{2}\lambda \left\| \omega \right\|^{2} \\ \end{aligned}$$
(4)

where Ω shows the regularization term that helps to reduce overfitting by reducing the model's complexity; l stands for a loss function that is differentiable and convex; γ is the minimal loss reduction required to split a new leaf; and λ displays the regulation coefficient. It is worth noting that in these equations λ and γ assist to increase model variance and avoid overfitting.

The objective function for each individual leaf is reduced in the gradient boosting technique, and additional branches are added sequentially.

$$L^{(t)} = \sum\limits_{i = 1}^{n} {\left\{ {l(y_{i} ,\hat{y}_{i}^{(t - 1)} ) + f_{t} (X_{i} )} \right\}} + \Omega (f_{t} )$$
(5)

The t-th iteration of the above-mentioned training procedure is represented by t. The XGBoost method aggressively adds the space of regression trees to greatly improve the ensemble model, which is sometimes dubbed "greedy algorithm". As a result, the model output is updated continuously by minimizing the objective function:

$$\hat{y}_{i}^{(t)} = \hat{y}_{i}^{(t - 1)} + f_{t} (X_{i} )$$
(6)

The XGBoost takes use of a shrinkage technique in which newly added weights are scaled by a learning factor rate after each stage of boosting. This minimizes the risk of overfitting by reducing the impact of future additional trees on each available individual tree96.

Light gradient boosting machine (LightGBM)

LightGBM is a novel gradient learning framework based on the decision tree concept. The main advantages of LightGBM over XGBoost are that it uses less memory, uses a leaf-wise growth method with depth constraints, and uses a histogram-based technique to speed up the training process. LightGBM discretizes continuous floating-point eigenvalues to k bins through using the aforementioned histogram technique, resulting in a k-width histogram. Furthermore, the histogram technique does not require additional storing of pre-sorted results, and values may be stored in an 8-bit integer after feature discretization, reducing memory usage to 1/8. Despite this, the model's accuracy suffers as a result of the harsh partitioning method. LightGBM also employs a leaf-by-leaf technique, which is more successful than the usual level-by-level strategy. The reason for this inefficiency in level-wise approach is that at each step, only leaves from the same layer are examined, resulting in unnecessary memory allocation. Alternatively, at each stage of the leaf-wise method, the algorithm finds the leaves with the largest branching gain, and then proceeds to the branching cycle. In comparison to the horizontal direction, errors can be reduced and greater precision can be attained with the same number of segmentations. The leaf-wise tree development technique is illustrated in Fig. 2. The disadvantage of leaf orientation is that it forces you to build deeper decision trees, which invariably leads to overfitting. On the other hand, LightGBM prevents overfitting while maintaining high efficiency by imposing a maximum depth restriction on the leaf top97,98.

Figure 2
figure 2

Leaf-wise tree development in LightGBM.

Full size image

For a specific training dataset \(X = \left\{ {(x_{i} ,y_{i} )} \right\}_{{_{i = 1} }}^{m}\), LightGBM searches an approximation \(\hat{f}\left( x \right)\) to the function f*(x) to minimize the expected values of specific loss functions L (y, f (x)):

$$\hat{f}\left( x \right) = \arg \mathop {\min }\limits_{f} E_{y,x} L(y,f(x))$$
(7)

LightGBM ensembles many T regression trees \(\mathop \sum \limits_{t = 1}^{T} f_{t } \left( x \right)\) to approximate the model. The regression trees are defined as wq(x), \(q \in \left\{ {1, \, 2, \ldots ,N} \right\}\), where q shows the decision rule of trees, N is defined as the count of tree leaves, and w denotes a vector shows the sample weights of leaf nodes. The model is trained in the additive form at step t:

$$G_{t} \cong \sum\limits_{i = 1}^{N} {L(y_{i} ,F_{t - 1} (x_{i} ) + f_{t} (x_{i} ))}$$
(8)

To estimate the objective function, the newton's approach is employed.

Gradient boosting with categorical features support (CatBoost)

CatBoost, which employs one hot max size (OHMS) that is a permutation technique beside the target-based statistics, employs categorical columns for categorical boosting. For a new split of the present tree, a greedy approach is utilized in this methodology, allowing CatBoost to identify the exponential evolution of the feature combination99. In CatBoost, for each feature with more categories than OHMS, the following steps are applied:

  1. 1.

    Records are divided into subsets at random.

  2. 2.

    Integer conversion of labels

  3. 3.

    Convert categorical features to numeric values as follows:

    $$avg\;Target = \frac{countInClass + prior}{{totalCount + 1}}$$
    (9)

where \(countInClass\) is the number of targets having a value of one for a category attribute, and \(totalCount\) is the number of preceding objects (the starting parameters specify prior to count objects)100,101.

Equations of state (EOSs)

EOS is a mathematical expression for the connection among a substance's volume, temperature, and pressure. This equation may be used to explain VLE, volumetric behavior, and thermodynamic properties of mixtures and pure substances. EOSs are used to estimate the phase behavior of petroleum fluids. As previously stated, EOSs have poor predictors of gas solubility in solvents, particularly under complicated working circumstances. Five EOSs were used to assess N2 solubility in hydrocarbons in this research, and their reliability in predicting N2 solubility is compared to ML algorithms. Mathematical equations of implemented EOSs are shown in Table 3. Table 4 also shows the parameters of the EOSs. Also, some required molecular parameters corresponding to each substance which is investigated with PC-SAFT EOS are provided in Table 5. Besides, a proper mixing rule is needed to use for estimation of each mixture’s parameters. In this study, van der Waals one-fluid mixing rules have been utilized, and its corresponding mathematical expression is provided in Table 4.

Table 3 EOSs Formulas utilized in this study.
Full size table
Table 4 Parameters of EOSs and mixing rules.
Full size table
Table 5 Parameters of PC-SAFT EOS105,108,109.
Full size table

Evaluation of models

The following statistical parameters, namely root mean square error (RMSE), standard deviation (SD), and coefficient of determination (R2) were used in this survey to evaluate the performance of models:

$$RMSE = \sqrt {\frac{1}{Z}\sum\limits_{i = 1}^{Z} {\left( {NS_{i,\exp } - NS_{i,pred} } \right)}^{2} }$$
(10)
$$R^{2} = 1 - \frac{{\sum\limits_{i = 1}^{Z} {(NS_{i,\exp } - NS_{i,pred} )^{2} } }}{{\sum\limits_{i = 1}^{Z} {(NS_{i,\exp } - \overline{{NS_{\exp } }} )^{2} } }}$$
(11)
$$SD = \sqrt {\frac{1}{Z - 1}\sum\limits_{i = 1}^{Z} {\left( {\frac{{NS_{i,\exp } - NS_{i,pred} }}{{NS_{i,\exp } }}} \right)}^{2} }$$
(12)

where Z, NSi,exp, and NSi,pred are the count of data, experimental N2 solubility, and predicted N2 solubility in normal alkanes, respectively.

On the other hand, the following graphical tools were utilized simultaneously to evaluate the performance of the ML models:

Cross plot: The most well-known graphical analysis in which the predicted values are plotted against the measured values and the accuracy of the models is evaluated by examining the proximity of the data points to the unit slop line.

Trend plot: This plot helps to check the validity of the model by sketching both real data and the model's estimation versus the specific property or data index.

Error distribution plot: The error (measured value − predicted value) is plotted against the real data to assess the scatter of data around the zero-error line and to explore the possible error trend.

Histogram plot of errors: This graph shows how the errors from the model are distributed. This statistical tool indicates the discrepancy between the measured and predicted values, in which a normal distribution centered at zero error is expected for a good model.

Results and discussion

Model optimization and tuning

To find the best model in each aforementioned algorithm, a routine procedure has been done to find the hyperparameters and the other functional features of each model. Since these models have been implemented in python, different libraries including scikit-learn for k-NN and Random forest110, xgboost for XGBoost, lightgbm for LightGBM98, and catboost99 for Catboost have been employed in this study. In each of these involves some parameters that should be set by user or they can be work on default mode. To find the best model state in each of algorithms, a wide range of selective parameters have been selected and the best model based on the training and test data RMSE has been chosen. The search space and the final arrangements of model are provided in Table 6.

Table 6 Models' tuning search space and selected model based on RMSE.
Full size table

Statistics and performance metrics of the models

The model’s precision in predicting N2 solubility in normal alkanes was assessed statistically based on several statistical criteria including RMSE, R2, and SD. Table 7 reports the calculated values of these statistical factors for the training subset, testing subset, and the entire dataset of all ML models. The possibility of overtraining is completely rejected given that no meaningful difference was seen between the testing and training subsets for all models. Based on Table 7, the CatBoost model has the lowest prediction errors among the developed ML models with RMSE values of 0.0125, 0.0213, and 0.0147 for the training subset, testing subset, and the entire dataset, respectively. Also, the overall R2 of 0.9943 for the CatBoost model is higher than other models and has a lower SD, indicating a better fit for this model to the experimental data. Moreover, random forest, XGBoost, LightGBM, and k-NN models are categorized after the CatBoost model in terms of good performance, respectively.

Table 7 ML models’ statistics and performance metrics.
Full size table

As mentioned earlier, several EOSs have been used comparatively with the ML models to estimate N2 solubility in normal alkanes. Hence, the solubilities of N2 in several normal alkanes namely Hexadecane, Eicosane, Octacosane, and hexatriacontane, which experimental values have been reported in the literature29,90, are estimated utilizing ML models and EOSs. Tables 8, 9, 10 and 11 represented the N2 solubility data and predictions of EOSs and ML models along with RMSE values for each of them. As can be seen, the CatBoost model provides the best estimates among the ML models and EOSs for the N2 solubility in all considered normal alkanes. ZJ EOS also had precise estimations for solubility values and outperformed other EOSs. On the other hand, as shown in Table 3, the Péneloux-type volume translation (c) has been used in the PR and SRK EOSs for the sake of investigation. Based on our studies, Péneloux-type volume translation does not have any effect on the obtained solubility values111,112.

Table 8 Estimations of different EOSs and ML models for N2 solubility in Hexadecane.
Full size table
Table 9 Estimations of different EOSs and ML models for N2 solubility in Eicosane.
Full size table
Table 10 Estimations of different EOSs and ML models for N2 solubility in Octacosane.
Full size table
Table 11 Estimations of different EOSs and ML models for N2 solubility in Hexatriacontane.
Full size table

Graphical analysis of the models

In the next step, the evaluation of the ML models is performed by graphical analysis. First, cross plots of the experimental N2 solubility data versus predicted values by the ML models for the training and testing stages are presented in Fig. 3. All five ML models performed well in both training and testing stages and most of the data points are accumulated around the X = Y line, although the scatter of points is much less for the CatBoost model and is more concentrated around the X = Y line, indicating the excellent performance of this model in estimating N2 solubility in normal alkanes.

Figure 3
figure 3

Cross plots of experiments vs predictions for the ML models.

Full size image

Next, the distributions of the N2 solubility prediction errors (measured—predicted) utilizing the ML models versus the experimental data are shown in Fig. 4. High concentrations of near-zero error points for a predictive tool indicate a better performance of that predictive tool in predicting N2 solubility in normal alkanes. Again, the CatBoost model resulted in near-zero errors, verifying its accuracy and reliability. However, other ML models especially random forest shows good predictions with low errors for the N2 solubility in normal alkanes.

Figure 4
figure 4

Prediction error distributions of ML models.

Full size image

The next step of the graphical assessment of introduced ML models for the prediction of N2 solubility in normal alkanes is related to the frequency of errors. Figure 5 depicts the histograms of errors corresponding to the proposed ML models in this work. As it is clear, the symmetric distributions are seen in the histogram graphs of all ML models. Also, the bursts of growing at the zero-error value for all developed models confirm the superb match between estimated and experimental data of N2 solubility in normal alkanes. However, the percentage frequency of errors at the zero-error value is about 85% for the CatBoost model and it is much higher than other ML models indicating the high credit of this model in estimating N2 solubility in normal alkanes.

Figure 5
figure 5

Histograms of errors for the ML models.

Full size image

However, all the models used in this study show satisfactory performances. As it is obvious from the statistical and graphical analyses, the CatBoost model shows the best performance among the implemented ML models. The performance of a model depends on many factors, such as the case of study and the structure of the dataset, and this superiority in performance for this model stems from two main reasons. The first one is the structure of the dataset used in this work, based on the shape of the dataset, there are many instances that have equal values in the n-1 feature and their only difference is in one feature. This feature enables the tree-based models to do a better splitting operation and finally brings higher accuracy. Secondly, Catboost models use symmetric trees and it helps to have a faster inference. Also, its boosting schemes are the main reason which avoids overfitting and increases the model quality after the training process. Finally, it should be noted that these advantages for Catboost strongly depend on the dataset and it cannot be generalized to all problems.

Pressure and temperature trend analysis

As the final assessment step, various visual evaluations were executed to appraise the CatBoost model's capability in various N2 solubility in hydrocarbons systems. Figure 6 represents the effect of pressure on N2 solubility for n-Decane system at the temperature of 503 K. Figure 6 shows N2 solubilities estimated by the CatBoost model for this case, as well as the values determined by the EOSs along with the literature experimental results87. The mismatch between standard EOSs estimations and actual experimental data is quite significant at high temperatures. As seen in this figure, the CatBoost model predicts experimental data quite well. Based on expectations, the solubility of N2 in n-Decane rises as the pressure increases. Meanwhile, the EOSs overestimate or underestimate the N2 solubility ‘growth when pressure rises, while the CatBoost model strictly traces the trend.

Figure 6
figure 6

Pressure trend analysis of N2 solubility based on the results of various EOSs and Catboost ML model for n-Decane at T = 503 K.

Full size image

The predictions of CatBoost and other proposed ML models for N2 solubility data in a light hydrocarbon (methane)61 under various operation conditions at a constant temperature of 180 K are provided in Fig. 7. All the intelligent models follow the trend well, and show a positive trend in N2 solubility as pressure increases. The CatBoost model, as shown in this figure, accurately recognizes data patterns and provides excellent estimations in all pressures.

Figure 7
figure 7

Pressure trend analysis of N2 solubility based on the results of implemented ML models for Methane at T = 180 K.

Full size image

Finally, a similar trend analysis performed to investigate the performance of different ML models at various temperature states to estimate the N2 solubility in n-hexane at the constant pressure of 27.57 MPa74. Based on Fig. 8, similar to the previous case, a satisfactory trend capturing is observed in all the intelligent models. However, the Catboost model provides more accurate predictions. Also, the figure indicates an increase in N2 solubility as temperature rises.

Figure 8
figure 8

Temperature trend analysis of N2 solubility based on the results of implemented ML models for n-hexane at P = 27.57 MPa.

Full size image

Sensitivity analysis

Utilizing the CatBoost model as the best-developed model in the current study, a sensitivity analysis was performed. To this end, the relevancy factor (r)113 was calculated for each input parameter using the following equation, with the knowledge that the higher the r-value, the greater impact on the model's output. It should also be noted that the positive r-value for a parameter indicates its direct effect on the output of the model and vice versa114.

$$r(I_{i} ,NS) = \frac{{\sum\limits_{j = 1}^{n} {\left( {I_{i,j} - I_{m,i} } \right)\left( {NS_{j} - NS_{m} } \right)} }}{{\left( {\sum\limits_{j = 1}^{n} {\left( {I_{i,j} - I_{m,i} } \right)^{2} \sum\limits_{j = 1}^{n} {\left( {NS_{j} - NS_{m} } \right)^{2} } } } \right)^{0.5} }}$$
(13)

where Ii,j represents the jth value of the ith input variable (i is molecular weight of normal alkanes, pressure, and temperature); Im,i shows mean value of the ith input; NSm and NSj denote the mean value and the jth value of predicted N2 solubility in normal alkanes, respectively. The outcomes of the relevancy factor analysis are depicted in Fig. 9. According to Fig. 9, all input parameters, namely temperature, pressure, and molecular weight of normal alkanes have a positive effect on N2 solubility in normal alkanes. The results reveal that the pressure has the greatest impact on N2 solubilities in normal alkanes and the N2 solubility increases with increasing the molecular weight of normal alkanes. Based on Henry's law, the amount of dissolved gas in a liquid is proportional to its partial pressure in equilibrium with that liquid. When the gas is at a higher pressure, its molecules collide more with each other and with the liquid's surface. As the molecules collide more with the surface of the liquid, they can squeeze between the liquid molecules and thus become a part of the solution115,116. On the other hand, the sensitivity analysis overall shows that the solubility of N2 in normal alkanes increases when the temperature increases. This shows the reverse order solubility phenomenon that is the opposite of what commonly happens for a binary mixture of a supercritical component and a subcritical component73,81. The reason for this may be due to the repulsive nature of N2–N2 interaction. The N2–N2 repulsive force decreases with an increase in temperature, which results in increased solubility of N2 at higher temperatures. However, increasing the solubility of N2 with an increase in temperature may not be true for all normal alkanes and literature survey shows that the N2 solubility in methane and ethane decreases with increasing temperature117. Normal alkanes are nonpolar, as they contain nothing but C–C and C–H bonds. N2 is also a nonpolar molecule and nonpolar substances tend to dissolve in nonpolar solvents such as normal alkanes. The molecular weight of the normal alkanes is mainly increased by adding C–C and C–H bonds. The obvious consequence of this is that the N2 solubility increases as the number or length of the nonpolar chains increases.

Figure 9
figure 9

Relevancy factor analysis.

Full size image

Conclusions

In the present work, N2 solubility in normal alkanes (nC1 to nC36) was modeled using five representative ML models namely CatBoost, k-NN, LightGBM, random forest, and XGBoost by utilizing a large N2 solubility databank in a wide range of operating temperature (91.21–703.4 K) and pressure (0.0212–69.12 MPa). Also, five EOSs namely RK, SRK, ZJ, PR, and PC-SAFT were used comparatively with the ML models to estimate N2 solubility in normal alkanes. The developed CatBoost model was superior to all of ML models and EOSs with an overall RMSE of 0.0147 and R2 of 0.9943. Moreover, Random Forest, XGBoost, LightGBM, and k-NN models were ranked after the CatBoost model in terms of good performance, respectively. Furthermore, ZJ EOS showed the best performance among the EOSs. Finally, the results of relevancy factor analysis indicated that all input variables to the models, namely temperature, pressure, and molecular weight of normal alkanes have a positive effect on N2 solubilities in normal alkanes and pressure has the greatest effect among these input variables. The solubility of N2 increases with increasing the molecular weight of normal alkanes.