Introduction

Soil is a complex matrix of varying organic and mineral composition, water and with different particle sizes. Soil spectra in the visible and infrared can be used to characterise soil. These spectra result from the interactions between electromagnetic radiation (between 400 to ~20,000 nm) and soil chemical and physical components1. Since a spectrum contains information on the fundamental compositing of soil, spectra can be used to estimate functional soil properties such as soil organic carbon (SOC). Diffuse reflectance in the visible and near infrared (vis–NIR) has been used for this purpose. The technique is rapid, cost-effective, non-destructive, and non-polluting. Additionally, a single spectrum, can be used to estimate different soil properties including SOC, soil texture (clay, sand and silt contents), water, cation exchange capacity, and pH2. To estimate soil properties with spectra, one needs to develop spectroscopic models using a spectral library. For this reason, many soil spectral libraries have been developed, at various scales, i.e. global3, continental4, national5,6,7,8,9,10 and regional11.

Vis–NIR spectra are highly collinear and absorptions are broad and overlapping, making it difficult to assign specific spectral features to soil properties2. Various spectral preprocessing methods are commonly used to remove noise, extract information from the spectra and improve the performance of the spectroscopic models, which describe the establishment of the relationship between the spectra and soil properties2. Statistical methods, such as partial least squares regression12, have been used to model soil properties with spectra. More recently, other non-linear methods including machine learning have also been used13. They include methods such as random forest14, support vector machine15, artificial neural networks16.

Recent spectroscopic modelling has shown that convolutional neural networks (CNNs) can potentially outperform conventional statistical and machine learning models. CNNs are a subset of deep learning, with successful applications in domains such as image classification17, video analysis18, drug discovery19. They are well-known for extracting useful local correlations in the data20. To utilise this feature for soil property prediction with spectra, researchers have developed various CNNs with one-dimensional (1D-CNNs)21,22,23 and two-dimensional structures (2D-CNNs)24,25,26. The 1D-CNNs process one-dimensional arrays, e.g. soil spectra, whereas 2D-CNNs use two-dimensional data with contextual information. Spectrograms derived from soil spectra were used in 2D-CNNs24. However, these spectrograms, which are essentially an image of stacked spectra, lack that 2D contextual information used in 2D-CNNs. So, unsurprisingly, 1D-CNNs produced more accurate spectroscopic predictions of soil properties compared to 2D-CNNs23.

A typical CNN can have a large number of hyperparameters, and their selection is critical to the CNN’s performance. To find the set of hyperparameters that generates optimal model performance, one needs to employ hyperparameter tuning, or optimisation27 (HPO). None of the CNNs for soil spectroscopic modelling reported in the literature21,22,23,24,26 have undertaken a thorough hyperparameter search, often relying on only manual tuning. Not using HPO may fail to fully exploit the capability of CNNs, and the lack of information about the tuning process can also affect the reliability of the models. Additionally, the manual tuning used in these studies can be tedious and time-consuming.

Here, we propose a framework to automatically optimise the tuning of hyperparameters in 1D-CNNs and to obtain insights into the tuning process. The aims of our study are to: (i) establish a parametric representation of 1D-CNNs for modelling SOC with a large spectral library, (ii) use a Bayesian optimisation algorithm to derive an optimal 1D-CNN architecture, maximise model performance and accurate estimates of SOC, and (iii) conduct hyperparameter importance analysis to better understand the effect of various hyperparameters on the model’s performance.

Hyperparameter optimisation of 1D-CNNs

1D-CNN hyperparameters

A typical 1D-CNN consists of a number of convolutional, pooling, and fully-connected layers. Batch normalisation28,29 and Dropout30 layers can also be included for faster training and better generalisation. A 1D-CNN is defined by specifying the relative locations of these layers and their associated hyperparameters.

A convolutional layer has hyperparameters that describe the number of filters, the kernel size, the stride, and the type of padding to use. The number of filters determines the number of feature maps that can be generated after a convolution; the kernel size gives the size of the filters; the stride defines the step size for sliding the kernel along the input array; the padding type specifies the method for dealing with the input arrays’ borders (e.g. by adding zeros).

A pooling layer has hyperparameters that are similar to those in a convolutional layer. In this case, they describe the pooling type, that is, Average pooling or Max pooling, the pool size to define the size of the pooling region, the stride size and the type of padding to use. A fully-connected layer has one hyperparameter, that is, the number of units in the layer. A batch normalisation layer has no hyperparameters. A dropout layer has one hyperparameter, the dropout rate, which is the probability to retain a unit.

Nonlinear activations enable neural networks to learn complex relationships between features (or predictors) and targets (or predictands). Commonly used activations are ReLU31,32, Leaky Rectified Linear Unit (LeakyReLU)33, exponential linear unit (ELU)34, scaled exponential linear unit (SELU)35, and Swish36. Modern deep neural networks use mini-batch gradient descent to update their weights37,38,39,40. Several optimisers have been developed for this purpose, such as Adagrad41, RMSprop37, and Adam42. Batch size is the number examples in a mini-batch. There usually exists a threshold after which the model starts to deteriorate43.

Hyperparameter optimisation (HPO)

HPO aims to solve the problem of finding the best set of hyperparameters that maximise a model’s performance27. It can be expressed as:

$$\begin{aligned} \varvec{\lambda }^*=arg \min _{\varvec{\lambda } \in \varvec{\Lambda }} \frac{1}{k} \sum _{i=1}^{k} \varvec{L}\left( \varvec{\lambda }, \varvec{D}_{train}^{(i)}, \varvec{D}_{valid}^{(i)}\right) \end{aligned}$$
(1)

where \(\varvec{\lambda }\) denotes a vector of hyperparameters; \(\varvec{\lambda }^*\), the vector of the optimal hyperparameters; \(\varvec{\Lambda }\), the hyperparameter space; k, the number of folds used in cross-validation; \(\varvec{L}\), the objective function for evaluating model performance on each fold; \(\varvec{D}_{train}^{(i)}\) and \(\varvec{D}_{valid}^{(i)}\), the datasets for training and validation in the ith fold, respectively.

Current HPO methods include manual search, grid search44,45, random search46, gradient-based methods47,48,49,50,51, Bayesian optimisation52,53,54, adaptive resource allocation55,56, and population-based methods57,58. The most important criterion for choosing a HPO algorithm is the nature of the hyperparameter space. The hyperparameter space in spectroscopic modelling is high-dimensional, mixed-typed (continuous and categorical hyperparameters), and tree-structured (conditional hyperparameters). It is an extremely complex space that many algorithms fail to work on. Sequential Model-based Algorithm Configuration (SMAC) and Tree Parzen Estimators (TPE) are able to search through such a hyperparameter space efficiently59. The TPE algorithm is also suitable for hyperparameter importance analysis as it evaluates all the folds in cross-validation and returns the overall objective for each hyperparameter configuration.

Bayesian optimisation—the TPE algorithm

A Bayesian optimisation algorithm consists of two main components: a surrogate function and a performance metric. The surrogate function is a computationally efficient approximation of the real objective function, which updates as the optimisation progresses. The performance metric, together with the surrogate function, proposes a new hyperparameter configuration for the next evaluation. The TPE algorithm uses Tree Parzen Estimator as the surrogate function and the Expected Improvement as the performance metric. Details about the TPE algorithm can be found in52.

The TPE algorithm starts with a number of evaluations on randomly sampled hyperparameter configurations. The optimisation history (\(\varvec{H}\)), which consists of hyperparameter vector and objective value pairs, can then be established using the completed evaluations. The algorithm then uses \(\varvec{H}\) to update the surrogate function and to select the next configuration of the hyperparameters (\(\varvec{\lambda _N}\)). After the evaluation of \(\varvec{\lambda _N}\), the optimisation history \(\varvec{H}\) is updated. The algorithm continues proposing and evaluating new hyperparameter configurations until a stopping criterion is reached. The TPE algorithm is summarised in Algorithm 1.

figure a

Results

In the Methods section below, we describe the dataset used, the parametric representation of the 1D-CNN, the hyperparameters, their values, and the optimisation.

Hyperparameter search histories

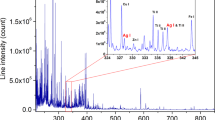
Hyperparameter search histories for random search and Bayesian optimisation are compared in Fig. 1. Both the objective values in the search methods decreased as hyperparameter search progressed. The Bayesian optimisation plateaued at 80 trials (9 h and 51 min) whereas random search needed 250 trials to level-off (24 h and 12 min). The Bayesian optimisation approach was approximately 3.1 and 2.5 times faster than random search in terms of number of trials and computational time, respectively. It returned a smaller minimum objective than random search (Fig. 1).

Figure 1
figure 1

Comparison of the hyperparameter search history from random search and the Bayesian optimisation.

Full size image

Optimal hyperparameters

The hyperparameters of the optimal model are given in Table 1. Based on the input channel states, the model took four input channels: Reflectance, Absorbance, Absorbance + First derivative (ABS + D1), and Absorbance + Second derivative (ABS + D2) (see Methods, Fig. 7). The model involved only one convolutional block (Conv-block). It is simply a convolutional layer with an activation function. Batch normalisation, pooling, and dropout layers were all disabled in the Conv-block. The model used two Fully-connected blocks (FC-blocks) and batch normalisation and dropout layers were turned on in the FC-blocks.

Table 1 Optimal 1D-CNN hyperparameters.
Full size table

Architecture and performance

The architecture of the optimal 1D-CNN is shown in Table 2. Compared to other published 1D-CNNs21,23, our optimised model is very simple. Interestingly, such a simple model achieved the best performance in our study. The cross-validated SOC predictions are shown in Fig. 2. The optimal model produced an RMSE of \(9.67 \pm 0.51\) (s.d.) and an \({R}^2\) of \(0.89 \pm 0.013\) (s.d.).

Table 2 Optimal 1D-CNN architecture.
Full size table
Figure 2
figure 2

Observed vs predicted soil organic carbon (SOC) from a 10-fold cross-validation. The solid 1:1 line is drawn for reference.

Full size image

Hyperparameter importance

Importance of the hyperparameters are presented in Fig. 3. Training-related hyperparameters (optimiser, batch size, and number of epochs) greatly affected the performance of the model. Model architecture was also critical to model performance, shown by the larger relative importance of Conv-block numbers (Fig. 3). Other architectural hyperparameters had a lesser impact on the model. In terms of preprocessing methods, only ABS + D1 had slight importance while the importance of other methods were negligible. Thus, only a few hyperparameters were critical to the model’s performance, which aligns with previous findings46,60.

Figure 3
figure 3

Hyperparameter importance based on the optimisation history. Hyperparameters are classified into training-related, input channels, Conv-block, and FC-block.

Full size image

We further investigated the hyperparameters’ effects by visualising the trials on the important hyperparameters, as in Fig. 4. Each dot represents a trial given by certain hyperparameters. The optimisation preferred optimiser Adam, batch size around 1000, number of epochs close to 1500, and only one Conv-block, which aligns with the optimal hyperparameters in Table 1. The optimisation covered the entire hyperparameter value ranges suggesting a thorough search. It is also obvious that more evaluations happened around the optimal values, which indicates that TPE algorithm can focus on promising values rather than testing values randomly.

Figure 4
figure 4

Trials on the important hyperparameters. (a) Optimisers. (b) Batch size. (c) Number of epochs. (d) Number of Conv-blocks.

Full size image

Discussion

The parametric representation allowed us to construct 1D-CNNs based on a given set of hyperparameters. It enabled the establishment of an optimisation problem that can automatically discover the best hyperparameters. The TPE algorithm could search through a high-dimensional, mixed-typed, and tree-structured hyperparameter space. It converged quickly and achieved better results compared to random search. The method is also practical in terms of computation time. The parametric representation and Bayesian optimisation combined, simplified the development of 1D-CNNs for the spectroscopic modelling by automating the process. The framework is also suitable for other fixed-length 1D signals in different soil and environmental sciences and engineering applications.

Hyperparameter importance analysis can shed light on the model tuning process, which is often assumed to be “black-box”. It calculates the importance of the individual hyperparameters and identifies the most important ones. This informed hyperparameter search can increase our understanding of the trained model and its reliability.

The optimised 1D-CNN produced accurate predictions of SOC. It delivered better estimates compared to other published studies that used the same LUCAS dataset23,24 (Table 3).

Table 3 Comparison of CNNs.
Full size table

Based on the hyperparameter importance of the input channels, preprocessing vis–NIR spectra with ABS + D1 can help to improve prediction accuracy. However, the influence of other preprocessing methods was insignificant, which implies that an optimised 1D-CNN itself can extract such information from the raw spectra. Therefore, preprocessing vis–NIR spectra with ABS + D1 may help the development of spectroscopic models using 1D-CNNs.

The simplicity of the optimal 1D-CNN suggests that spectra are composed of relatively simple and low-level features. This is consistent with the nature of vis–NIR spectra, which are characterised by broad and weak vibrational modes in the NIR and electronic transitions in the visible range, giving soil spectra few, broad absorption features. Attempting to extract complex and high-level features using multiple convolutional layers is likely to affect performance, as shown in Fig. 4d. The optimal 1D-CNN did not use a pooling layer. A pooling layer usually serves to down-sample input features and to introduce local translation invariance20. The down-sampling can be alternatively achieved by using bigger stride size in convolutional layers. Introducing translation invariance in soil spectroscopic modelling may affect model performance, as the features in vis–NIR spectrum are located at specific wavelengths.

There are an increasing number of studies comparing new machine learning models for soil spectroscopic modelling. Some claim that their specific architectures outperform others. However, it is difficult to determine whether a model is better purely because of its unique architecture, or because it might have been tuned better. The problem is greater when the models are tuned manually, since it is impossible to guarantee the same amount of tuning to all the models. Thus, assessment of such machine learning models could be biased. The optimisation method in this study provides a way for unbiased assessment of models, as it can fully exploit different architectures.

We presented an approach for optimal, automatic spectroscopy modelling with 1D-CNNs. It simplified the development of the 1D-CNNs. It searched thorough a complex hyperparameter space and returned an optimal 1D-CNN that produced accurate estimates of SOC. The hyperparameter importance analysis provided insights into the tuning process, which gave us confidence in the reliability of the model.

Methods

The dataset

We used the Land Use/Land Cover Area Frame Survey (LUCAS) dataset which collected and analysed soil samples across Europe. Approximately 20,000 samples are publicly available each of which consists of a sample’s spectral signature and its corresponding physicochemical properties. The spectra cover a wavelength range from 400 to 2500 nm with resolution of 0.5 nm. We removed approximately 2000 samples from the downloaded LUCAS dataset because of errors that we could not explain in either the spectra or the soil properties or the geographic coordinates. Thus, the dataset that we used in our research has 17,607 samples. We downsampled the spectra by 1:20 to remove multicollinearily and to improve computational efficiency during the training of the models. Here, we only considered soil organic carbon (SOC) as the response, or target variable. The histogram of SOC’s distribution is shown in Fig. 5.

Figure 5
figure 5

Histogram of the soil organic carbon (SOC) content in the LUCAS dataset (\(\hbox {n} = 17{,}607\)), showing moments of its distribution. The dataset includes both mineral and organic soil.

Full size image

A parametric representation for 1D-CNNs

We described 1D-CNNs using three types of building blocks: Convolutional blocks (Conv-blocks), Fully-connected blocks (FC-blocks), and an Output block (Fig. 6a–c). A Conv-block stacks a convolutional, batch normalisation, activation, pooling, and a dropout layer in sequence. Similarly, an FC-block consists of a fully-connected, a batch normalisation, an activation, and a dropout layer. The output block is essentially a Fully-connected layer that outputs target values. Thus, a 1D-CNN can be defined by a number of Conv-blocks and FC-blocks, joined by a Flatten layer (Fig. 6d).

Figure 6
figure 6

1D-CNN building blocks. (a) Convolutional block. (b) Fully-connected block. (c) Output block. (d) Construction of a 1D-CNN using the blocks.

Full size image

We used state hyperparameters to turn ON/OFF the Pooling, Batch Normalisation, and Dropout layers. To generate multiple input channels, we considered five common preprocessing methods: reflectance (R), absorbance (\(= \hbox {log}~\hbox {R}^{-1}\)), absorbance + first derivative (ABS+D1), absorbance + second derivatives (ABS+D2), and absorbance + standard normal variate (ABS+SNV). Each channel has a state hyperparameter (ON/OFF) to indicate whether to use the channel for the modelling. Figure 7 shows examples of the input channels.

Figure 7
figure 7

Input channels derived from different preprocessing methods. (a) Reflectance. (b) Absorbance. (c) Absorbance + first derivative. (d) Absorbance + second derivative (e) Absorbance + standard normal variate.

Full size image

The hyperparameters and their values are summarised in Table 4. The value ranges some hyperparameters can be predetermined, while others need to be determined specifically for the particular problem.

Table 4 1D-CNN hyperparameters.
Full size table

Optimising 1D-CNNs for soil spectroscopic modelling

We used 10-fold cross-validation and the root mean squared error (RMSE) to fit and validate the 1D-CNNs for predicting SOC using the LUCAS dataset. From Eq. (1), the optimisation problem can then be expressed as:

$$\begin{aligned} \varvec{\lambda }^*=arg \min _{\varvec{\lambda } \in \varvec{\Lambda }} \frac{1}{10} \sum _{i=1}^{10} RMSE\left( \varvec{\lambda }, \varvec{D}_{train}^{(i)}, \varvec{D}_{valid}^{(i)}\right) \end{aligned}$$
(2)

where \(\varvec{\Lambda }\) denotes the hyperparameter space; \(\varvec{\lambda }\), a vector of hyperparameters in that space; \(\varvec{\lambda }^*\), the vector of the optimal hyperparameters; \(\varvec{D}_{train}^{(i)}\) and \(\varvec{D}_{valid}^{(i)}\), the spectral datasets for train and validation in the ith split respectively. RMSE calculates the root mean squared error using the predicted and observed values in dataset \(\varvec{D}_{valid}^{(i)}\), given a model fitted on \(\varvec{\lambda }\) and \(\varvec{D}_{train}^{(i)}\). The RMSE score on the 10 splits are averaged to form the overall objective.

Hyperparameters and their corresponding value ranges were those shown in Table 4. For the hyperparameters that are dataset-dependent, we set their value ranges based on recommended values in the literature and our experience with the dataset and 1D-CNNs. We employed Early Stopping61 when training the models to prevent overfitting. To assess the performance of the Bayesian optimisation-based approach we also ran a random search.

We conducted hyperparameter importance analysis to investigate the hyperparameters’ effects on the model performance. The hyperparameter importance was calculated using functional Analysis of Variance60, which requires an optimisation history that consists of records of hyperparameter configurations and its corresponding objective value. Since the algorithm computes the importance of the hyperparameters that exist in all records, we only calculated the importance for independent hyperparameters.