Abstract
In this experimental study we film the landings of Aedes aegypti mosquitoes to characterize landing behaviors and kinetics, limitations, and the passive physiological mechanics they employ to land on a vertical surface. A typical landing involves 1–2 bounces, reducing inbound momentum by more than half before the mosquito firmly attaches to a surface. Mosquitoes initially approach landing surfaces at 0.1–0.6 m/s, decelerating to zero velocity in approximately 5 ms at accelerations as high as 5.5 gravities. Unlike Dipteran relatives, mosquitoes do not visibly prepare for landing with leg adjustments or body pitching. Instead mosquitoes rely on damping by deforming two forelimbs and buckling of the proboscis, which also serves to distribute the impact force, lessening the potential of detection by a mammalian host. The rebound response of a landing mosquito is well-characterized by a passive mass-spring-damper model which permits the calculation of force across impact velocity. The landing force of the average mosquito in our study is approximately 40 \(\upmu\)N corresponding to an impact velocity of 0.24 m/s. The substrate contact velocity which produces a force perceptible to humans, 0.42 m/s, is above 85% of experimentally observed landing speeds.
Similar content being viewed by others
Introduction
Insect flight is an enduring topic, with numerous studies on takeoff1,2,3, in-flight mechanics4,5,6, and landing7,8,9. Landings are unique from other flight maneuvers because they require matching the relative motion of a target, demanding highly-coordinated movements in response to visual, thermal, acoustic, and olfactory signals10,11,12,13,14,15. Landings are initiated to intercept prey, forage from dynamic surfaces, and perch to rest and nest16,17. Frequent feeding requires flying insects to engage dynamic targets, from flowers swaying in a breeze to mammals in motion, and the mosquito provides an example of an animal which engages both animate and inanimate nutrition sources. Mosquitoes are notorious for covertly feasting on blood, a process which begins with landing and is accomplished across a range of relative velocities and surface orientations18. Aedes (Ae.) aegypti mosquitoes are among the most prolific and dangerous mosquito species globally19,20,21, and like all mosquitoes, rely on blood meals for maturation of eggs22,23. Remaining undetected by the host during landing, feeding, and takeoff maximizes the probability of a successful meal. Despite their relevance to society, passive and active mechanisms by which mosquitoes initialize this process are understudied. The study of aerial landings across a variety of physiology, and under a plethora of environmental pressures, is not only imperative to understanding biological mechanisms, but may also be extended to the adaptation and survivability of emerging small unmanned aerial systems (SUAS) on the scale of insects24.
Mosquitoes, like many insects, navigate their environments through a combination of visual and olfactory cues and the act of host-seeking has received much attention in regard to attraction to scents25, patterns26,27, colors28, and illumination29. Historically, the vast majority of insect vision studies have been performed with fruit flies (Drosophila melanogaster)30,31. Mosquitoes possess a similar neurological construct to that of fruit flies32, who can be conditioned to discern different patterns with the aid of a sucrose stimulus33. Previous studies of mosquito vision have focused on site selection preference driven by site color (wavelength) and patterning. Gravid Ae. albopictus adults prefer solid black ovitraps as opposed to lighter colored ovitraps28. Ae. aegypti mosquitoes show greater responsiveness to color than the shape or pattern of ovitraps26. Indeed, Ae. aegypti prefer to land on darker surfaces of hosts and surfaces of low reflectance, supporting the assertion of their craftiness23,34,35. Anopheles gambiae females, by comparison, are capable of associative pattern recognition and able to localize a food source on both checkered and concentric patterns of black and white, according to their conditioning27. Landing is the final stage in host-seeking behavior, which must be completed such that the host cannot thwart the mosquito mission for a blood meal.
The landing strategies of insects differ from those of vertebrates in both timescale, distance, and speed due to highly contrasting anatomy and function. Insects’ immobile eyes and fixed focus optics prevent binocular stereopsis to gauge the distance from a substrate outright9,36,37. Insects instead use image motion to determine substrate distance. They monitor object expansion relative to their own motion, and control flight based on the rate of change of perceived object size11,17. Honeybees (Apis mellifera) decelerate to a hover 16 mm from a landing surface, demonstrating that touchdown is modulated through relative distance17,38, and initiate touchdown with legs on vertical walls whilst pitching their abdomen to dissipate residual flight energy39. Similarly, hawkmoths (Macroglossum stellatarum) decelerate upon approaching a flower and hover before initiating touchdown40. A female housefly (Musca domestica) approaches a landing surface at a constant velocity until the object reaches a critical size on its retina to induce deceleration11. Upon approach to a vertical landing surface, legs extend and bodies pitch upward7, most likely as a means to decelerate–flight velocity and pitch are inversely related in houseflies41. In contrast, fruit flies (Drosophila melanogaster) accelerate towards their landing surface and, upon touchdown, use leg forces to undergo nearly instant deceleration8. Legs extend prior to inverted surface landings and upon touchdown legs also assist in body rotation for multiple appendage engagement42.
Detailed Ae. aegypti landing mechanics are absent from literature, to the authors’ knowledge, but are likely unique from other insects due to diet, wing mechanics4, physiological proportions, and mass. A mosquito has 1–10% the mass of a housefly, honeybee, and hawkmoth17,43, and twice that of a fruit flies with dramatically different flight mechanics44,45. Mosquito mass allows for survival of collisions with objects of much larger mass traveling at greater speeds46, but the influence of mass on landing has not been studied. Typical mosquito flight posture is characterized by fore, mid, and hind-legs raised and splayed, perhaps for the sake of reducing in-flight drag22.
In this experimental study we reveal the mechanisms mosquitoes employ to engage hosts with landing forces below which humans can sense47. We observe mosquito landings with high-speed cameras, seen in Fig. 1, and digitize their motion to quantify landing forces, the employment of various appendages, and the ability of mosquitoes to cleave to surfaces across a range of contact velocity with a static surface. We begin with a description of our experimental methods in “Experimental methods” section. We initiate “Results” section with a description of the landing sequence and follow with a presentation of kinematics, forces, and energy. We discuss implications of our results in “Discussion” section, and provide concluding remarks in “Conclusion” section.
Experimental methods
Mosquito rearing and care
Aedes aegypti eggs were obtained from the United States Department of Agriculture-Agricultural Research Service, Center for Medical, Agricultural and Veterinary Entomology (USDA-ARS-CMAVE, Gainesville, FL) and continued to be cultivated in the Willenberg Lab as described elsewhere48. Briefly, 8 mg of eggs (\(\sim 800\) eggs) are brushed off the cards and shaken vigorously in a glass vial containing 7.5 mL of larval food in deionized (DI) water (40:60; brewer’s yeast and liver powder). The solution is transferred into 3 L of DI water in a plastic tray. These trays are incubated at 29–30 \(^\circ\)C and larval food is added at day 3 (7.5 mL), day 4 and day 5 (10 mL). At day 6, the larvae/pupae are poured over a 500 \(\upmu\)m strainer, rinsed with fresh DI water and transferred to 200 mL of DI water in 237-mL (50 cm\(^2\) surface area) cups. These cups are placed in a (\(20.3\times 20.3\))-cm rearing cage and kept in a 29–30 \(^\circ\)C incubator. Within 24 h, most mosquitoes emerge and this counts as day post-emergence (DPE) one. Sucrose (10% w/v) is provided ad libitum via a saturated cotton ball placed atop the rearing cages. On DPE 3, the mosquitoes are cold anesthetized in a cold room for 30 min. The mosquitoes were then collected in a cup and kept on ice. As required, 50 male and 50 female mosquitoes are sorted into separate cups by spreading them on a plate kept on ice and grasping the hind legs for transfer. The cups are covered with screen mesh and 10% (w/v) sucrose provided ad libitum through small saturated cotton balls.
Landing experiments
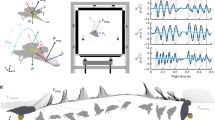
We film 20 landings of non-blood-fed female Ae. aegypti mosquitoes onto a rigid, vertical surface. Landings are filmed within a plastic 3D-printed flight arena lined with acrylic walls. The arena internally measures (\(70 \times 100 \times 140\)) mm (H \(\times\) W \(\times\) L), as seen in Fig. 1b. A purple substrate, the width of the container and 40 mm in height, is placed at one end of the arena to serve as the landing surface; darker hues elicit landings at a rate 9x higher than clear or white substrates29. Mosquitoes are anesthetized with CO\(_2\) for placement into the flight arena, and given sufficient time to recover from anesthetization before filming. To encourage resting mosquitoes into flight, the arena is vibrated at low amplitude 25 Hz for up to 5 s. Vibration does not catapult mosquitoes from walls and mosquitoes are given at least 1 s (\(\sim 600\) wingbeats)2 to recover flight before a landing is considered for analysis. The landing surface protrudes through the walls of the arena and is supported externally such that it does not vibrate with the arena walls. After cessation of vibration, only landings that originate from an orthogonal distance greater than 10 mm is saved for analysis to exclude landings influenced by adjacent wall or neighbor mosquito contact in the moments preceding landing. Landings were recorded on six individual days. Fifty mosquitoes are replaced into the container simultaneously after which multiple landings are recorded—3, 4, 7, 1, 2, 3 landings per recording day, respectively. A new group of 50 mosquitoes is used each filming day. We treat all landings as independent samples and acknowledge the probability of one pseudo-replicate for the entire experimental dataset is 24.6%.
Filming
Landings are filmed using Photron AX-100 and UX-100 high-speed cameras at (2000–4000) fps in single and dual camera configurations. All reported kinematic measurements are extracted from single camera experiments for the sake of measurement precision. We view landings from above with a 150-mm Nikon lens and measure the position and velocity in a horizontal plane orthogonal to the landing substrate. Mosquito kinematics are digitized with Open Source Physics Tracker (OSPT) by tracking where the proboscis meets the head in each video frame. OSPT is calibrated with a grid of known dimension in frame and tracks the spatial position of a specified point on the mosquito across frames. Two cameras are utilized for 3D reconstruction to visualize incoming flight path and bouncing sequences as shown in Fig. 1c. In two camera experiments, an additional camera is placed to view the landing surface in its entirety. The cameras are fitted with 60 mm (side) and 24–120 mm (top) Nikon lenses. 3D trajectories are extracted from paired videos with direct linear transformation, DLTdv649. Wing rotation values are taken from videos not used in extracting landing kinematics but instead view mosquitoes top-down.
Physical characterization
The proboscis is modeled as an end-loaded cantilever beam. Three proboscises were excised from the head and affixed to a rigid rod with UV-curable glue and filmed within 10-min of excision. A Keyence VHX-900 digital microscope, which has internal pixel calibration, is used to measure proboscis diameter and cantilevered length at a magnification of 150x. The Keyence VHX-900 also films the accumulation of water produced by an ultrasonic humidifier. All deposited moisture except a single droplet is removed manually before measurement. The deflection of the proboscis under the weight of the single droplet is measured optically by photographic measurements in OSPT. The experiment was replicated twice for each proboscis to achieve an average value. Damping characteristics are determined by using a modified cubic flight arena of characteristic length \(37.5\) mm to inhibit free flight and ground the mosquitoes. The mosquitoes are vibrated at a fixed frequency of 25 Hz and 50 Hz for a few seconds to establish sinusoidal behavior, and then vibration is ceased. Videos are analyzed with OSPT.
Results
Description of landing and orientation preference
The walls of the flight arena are briefly vibrated to encourage flight of resting mosquitoes. Mosquito landings are considered for analysis if a forward appendage (forelimbs or proboscis) initiates contact with the landing surface. All analyzed landings are shown in Fig. 2 as smoothed curves and in Fig. S1 as raw curves. Temporal velocity for all landings are is plotted in Fig. S2. Mosquito flight posture is characterized by both forelimbs projecting outward with \(\theta _\text {legs}=118.4 \pm 8.1^\circ\), \(\text {N}=5\) with respect to one another if measured from the thorax dorsal center. Typical flight posture is shown in Fig. 3a,c (Movie S1). Such a foreleg posture avoids lateral engagement of substrates up to an angle of incidence \(\alpha = \theta _\text {legs}/2 = 59.2 \pm 4.1^\circ\). We limit our scope of analysis to landings in which the angle of incidence of approach is less than \(\alpha\) to eliminate landings which were slowed, or otherwise influenced, by grazing contact of aft legs and wings prior to substrate engagement.
Normal-to-substrate displacement for all 20 analyzed landings. The tracked point on the mosquito is the interface of the proboscis with the head. The final resting position of the tracked point corresponds to \(x=0\). First contact of any portion of the mosquito with the landing surface corresponds to \(t=0\). Dashed-curves indicate the proboscis is the first member to contact the substrate, while solid lines indicate tarsi initiate contact. Curves are smoothed with a second-order Savitzky–Golay filter at 10% span.
Mosquitoes approach the test surface with a normal velocity \(v_\text {n} = -\,0.24 \pm 0.14\) m/s, \(\text {N}=20\), as shown in Fig. 2 for \(t<0\). Upon tarsal contact with the substrate specimens rapidly decelerate, shown graphically in Figs. 2 and 3a, b. Sensing of the substrate prior to touchdown is likely done with a combination of vision and self-induced pressure wave detection50. Encounters with the substrate intermittently occur proboscis first, shown in Fig. 3d, and produce compression of the forelegs and often buckling/deformation of the proboscis, lengthening impact time, seen in Fig. 3e. Mosquitoes bounce from the surface at a normal velocity \(0.16 \pm 0.08\) m/s, N \(=\) 19, and reverse course back toward the substrate at an average distance of 1.7 mm. A bounce is witnessed when the torso experiences movement away from the substrate. Landings in which tarsi do not separate from the substrate following initial contact display a single bounce. A double bounce landing is plotted in three dimensions in Fig. 1c, two dimensions in Fig. 3a, and pictured in Fig. 3d–g. Only a single trial displayed no bounce. Mosquitoes display a bounce pattern which ceases when tarsal grip is sufficient to overcome bounce acceleration, within 3 bounces (Movie S2). Every bounce and subsequent approach acts to reduce the mosquitoes’ incoming momentum by at least 50%, N \(=\) 19. With forelimb tarsi securely in place, the abdomen and remaining legs swing downward to contact the surface as the wings cease flapping. Once coming to their resting position, Fig. 3g, wings then rotate inward at an average angular velocity \(12,977 \pm 4844\,{^{\circ }}\)/s, \(\text {N}=5\) (left wing) and \(12,943 \pm 4932\,{^{\circ }}\)/s, \(\text {N}=4\) (right wing) to rest atop the abdomen approximately 100 ms after approach, as pictured in Fig. 1a.
Mosquito landing plots for (a) Temporal normal-to-substrate displacement. (b) Temporal normal-to-substrate velocity. Data in plots (a) and (b) is smoothed with a second-order Savitzky–Golay filter at 10% span. (c) Initial deceleration of mosquito. (d) First contact of proboscis. (e) Collapse of the proboscis with head nearly contacting surface. (f) Maximum bounce displacement. (g) Final stabilization of landing position with eminent wing retraction.
While we analyze only landings onto vertical surfaces in this study, we do quantify the frequency of landings onto vertical and horizontal surfaces within our flight chamber. Over the time-course of 5 minutes, beginning at the cessation of arena vibration, we count the number of landings onto the purple substrate when oriented vertical and horizontal, in separate trials. For each trial, 50 female mosquitoes were placed in the arena simultaneously. We count \(29 \pm 3\), \(\text {N}=3\), landings on the vertical surface and a meager \(3 \pm 2\), \(\text {N}=3\), landings on the horizontally oriented surface, a result which is in line with previous observation of mosquito preference19. We note that for many mosquito hosts, humans for example, vertically oriented surface area exceeds that of horizontally-oriented surface area.
Impact energy and proboscis bending
As legs compress, wings flap, and proboscises deform, mosquitoes absorb their in-flight kinetic energy \(E_\text {k} = m v_\text {n}^{2}/2=0.061~\upmu\)J, where the average mosquito mass \(m=1.66\) mg, N \(=\) 30. In the absence of detailed wing kinematics and computational fluid dynamics, parsing the energy absorbed in the legs \(U_\text {l}\) from that absorbed by the wings \(U_\text {w}\) is not feasible, and is thus beyond the scope of the current study. Therefore, we quantify the energy absorbed \(U_\text {p}\) via proboscis deflection \(\delta _\text {p}\), preceding the initial bounce, seen in Fig. 4a, b (Movie S3). Proboscis deflection is not seen in subsequent bounces and was present in 16 of 20 recorded landings. Altogether we may write \(E_\text {k} = U_\text {p} + U_\text {l} + U_\text {w}\), and note that potential energy is neglected in our consideration of conservation of momentum in the direction perpendicular to the landing surface.
Deflection of the proboscis \(\delta _\text {p}\) is measured approximately 5–80%, \(\text {N}=16\), of proboscis length \(L=1.0-2.1\) mm. We acknowledge this degree of deformation very likely places the proboscis outside the linear-elastic regime. However, to gain an understanding of the role proboscis deformation plays in the landing process without knowing precise deformed curvature, we employ linear-elastic assumptions. We model the proboscis as an end-loaded cantilever beam where the proboscis deflection stores elastic strain energy \(U_\text {P} = k_\text {eff}\delta _\text {p}^{2}/2\) and force is applied normal to the beam axis. The effective stiffness of the proboscis \(k_\text {eff}\) can be written in terms of elastic modulus \(E_\text {p}\), area moment of inertia \(I = \pi r^4 /4 = {2.16} \times 10^{-6}\,{\hbox {mm}^4}\), and L, such that \(k_\text {eff}=3E_\text {p}I/L^{3}\), where proboscis radius \(r=43\pm 2\)\(\upmu\)m, \(\text {N}=3\). The elastic modulus of the proboscis is determined by measuring its deflection \(\delta _\text {D}\) under the weight \(F_\text {D}\) of a droplet (see “Experimental methods” section), such that
where the cantilevered proboscis length \(\ell = 917 \pm 97\,\upmu\)m, \(\text {N}=3\) and \(\delta _\text {D}= 3.2 \pm 1.3\,\upmu\)m, \(\text {N}=3\). Deflection of a proboscis by a drop can be seen in Fig. 4b, and schematized in Fig. 4c. We measure \(E_\text {p} = 1.56 \pm 0.16\) MPa, \(\text {N}=3\), and from above,
For the maximum observed value of \(\delta _\text {p} = 0.8L\) and \(L=1\) mm, \(U_\text {p}=0.0032 ~\upmu\)J. In the most extreme cases the proboscis is able to absorb up to \(U_\text {p}/E_\text {k} \approx 5.4\%\) of the kinetic energy of the average mosquito approach.
If instead we consider an axially loaded proboscis, the critical buckling load \(P_\text {cr}\) required to produce tip movement \(\delta _\text {p}\), analogous to buckling a column,
we calculate \(P_\text {cr} = {8.3}\,{\upmu \hbox {N}}\), well below the human detection threshold, 70 \(\upmu\)N47. The exact energy calculation associated with buckling would require extensive post-buckling analysis and is complicated by complex material behaviors at large deformation. Such characteristics are not known for proboscises. Recent research in the crushing of slender structures indicates a rapid collapse of load bearing capacity at the onset of instability for even complex structures under both axial and bending loads51,52. Conservatively, we assume linear force P degradation such that \(P=P_\text {cr}\) at loading onset and \(P=0\) at complete collapse. The energy transferred to the proboscis is the sum of the collapse energy \(U_\text {col}\approx P_\text {cr}L/2=0.0042\,\upmu\)J and the assumed negligible elastic energy. Thus, \(U_\text {col}/E_\text {k}\approx 6.9\%\). The agreement in values of \(U_\text {p}\) and \(U_\text {col}\) indicates the primary mechanisms for dissipating energy associated with orthogonal flight motion are leg compression and wing aerodynamics, discussed in “Impact force mitigation by foreleg properties” section.
Impact force mitigation by foreleg properties
Foreleg compression at touchdown lengthens impact time and reduces impact force by distributing momentum across multiple joints. Modeling the mosquito as a simple mass-spring-damper, where the legs act as the damped spring, allows for the determination of their effective damping coefficient c and stiffness k for comparison to those ideal for force reduction. To characterize dynamic response we vibrate the box floor beneath standing mosquitoes at a fixed frequency, 25 and 50 Hz. Upon nearly impulsive cessation of floor movement we measure free response of mosquito bodies and solve the corresponding equation of motion,
where \(\beta = c/m\) and \(\omega _\text {n} = \sqrt{k/m}\). The amplitude reduction factor provides the damping ratio \(\zeta\) of the mosquito,
where n is the number of cycles between amplitude measurements \(x_1\) and \(x_2\) equal to unity in our system (Fig. 5a). Solving Eq. (5) with both 25 and 50 Hz responses, \(\zeta _\text {exp} = 0.36 \pm 0.10\), \(\text {N}=8\), indicating the mosquito behaves as an underdamped system, explaining mosquitoes’ propensity to bounce after first contact. The natural frequency of the mass-spring-damper analog \(\omega _\text {n} = \omega _\text {d}/\sqrt{1-\zeta ^2}= 256 \pm 39\) rad/s, where \(\omega _\text {d}= 239 \pm 36\) rad/s is measured from spatio-temporal data. The spring constant \(k = m\omega _\text {n}^2= 0.109 \pm 0.002\) N/m, the critical damping coefficient \(c_\text {c}=\sqrt{4mk}= 8.5 \pm {1.2}\times 10^{-4}\) N-s/m, and the actual damping coefficient \(c = \zeta c_\text {c}= 3.1 \pm {0.5}\times 10^{-4}\) N-s/m. The general solution to Eq. (4) is,
where \(\gamma = \frac{1}{2}\sqrt{4\omega _\text {n}^2-\beta ^2}\), \(A= [\beta x(0)/2+{\dot{x}}(0)]/\gamma\), and \(B=x(0)\). Using the aforementioned values of k and c, we plot Eq. (6) in a dashed-black line next to a temporal track of a typical landing event, in Fig. 5b, matching the initial condition \(x(0)=2\) mm of the data. We note reasonable agreement with experimental data through the first 20 ms of landing. Equation (6) does not capture the influence of aerodynamic damping of the wings, the wing-in-ground effect, and potential coulomb damping in the joints. Moreover, Eq. (6) predicts the mosquito will accelerate slightly, a consequence of modelling legs as damped, outstretched springs.
An improved fit may be garnered by prohibiting the virtual spring in the mosquito leg to be extended prior to impact, adding a constant bias C, and phase shift \(\phi\),
Equation (7) is fit to the raw experimental data in Fig. 5b with a nonlinear least squares solver, where C, D, \(\zeta\), \(\omega _\text {n}\), \(\omega _\text {d}\), and \(\phi\) are free parameters. We plot the best fit provided by Eq. (7) with a red curve in Fig. 5b. The resulting \(k=0.07\) N/m, \(c={1.6}\times 10^{-4}\) N-s/m, and \(\zeta = 0.23\) agree with those calculated from experiments of mosquito free vibration following an impulsively-stopped vibrating floor [Eq. (5)].
By setting \(B=x(0)=0\) in Eq. (6) and taking the second time derivative we produce an equation for temporal substrate force that utilizes k, c, and \(\zeta\) calculated through free vibration experiments,
A range of \({\dot{x}}(0)=v_\text {n}\) is used to plot F against t in Fig. 6. We plot only the first 10 ms, sufficient time for rebound to begin, as seen in Fig. 5b. We assume the mosquito distributes the load uniformly between two front legs and neglect aerodynamic effects. The slowest mosquito landing provides an impact acceleration of 0.6 gravities, while the fastest impact produces 5.5 gravities. The range of landing velocities in our study is in agreement with in-flight velocities recorded in other studies53,54,55. The landing force of the average mosquito in our study is approximately 40 \(\upmu\)N, falling short of human detection. However, covert landings are not universal as 3 trials (\(15\%\)) record a magnitude of normal velocity greater than that which meets the human force detection threshold47, 0.42 m/s. This result aligns with authors’ experience of occasionally sensing a landing mosquito, less common than sensing the mosquito bite.
The temporal substrate force from Eq. (8) for various landing velocities. Blue and red curves represent the slowest and fastest observed velocities, respectively, while the purple cone denotes the standard deviation around the average observed velocity.
Discussion
Our study reveals Ae. aegypti mosquitoes employ bouncing sequences, leg compression, and proboscis deformation to engage landing surfaces. Unlike bees38, houseflies7, and fruit flies8, we do not witness mosquitoes prepare for landing by adjusting leg posture or body rotation. Their substrate interactions often have head and torso contact with the substrate (Fig. 3e), but the associated forces are easily survivable and relatively small in the insect realm46. Proliferation mandates that landings are completed discreetly, below that which a host can sense, so that blood meals are completed unencumbered. Thus a mosquito employs multiple appendages to scrub momentum and reduce the force imparted by any one member. Any flyer, biological or engineered, aiming to land discreetly may control the effective length \(x_\text {eff}\) of impact over which flight is slowed under constant acceleration. Rearranging the equation of motion and assuming no reactions other than those provided by the substrate,
where \(F'\) is the landing force not to be exceeded. For mosquitoes we calculate \(x_{eff } = 1.4 \pm 0.5\) mm for initial impact if using \(F'=70\,\upmu\)N. This value of \(x_\text {eff}\) would be traveled in \(\sim\)6 ms, is \(\approx 23\%\) of a mosquito body length22, and \(\approx 33\%\) of the mosquito foreleg, appears exceedingly achievable. Yet, we observe greater compression distances by the proboscis alone, \(\delta _\text {P} = 1.71\) mm, an observation that may be tied to insect perception rather than kinetics. However, it was recently discovered mosquitoes can sense sound pressure waves generated by their flapping wings rebounding from nearby surfaces, a sensory cue that is used to divert from unavoidable surfaces50.
While the timescale over which landings occur is rapid, it is comparable to the timescale of takeoff2 and lengthy compared to the timescale of a single wingbeat56. Thus, it is possible leg compression at landing is not wholly passive. Active engagement of leg muscles may contribute to the discrepancy between our passive model and experimental response of a landing mosquito. An active force modifier may be added to Eq. (4) to better match mosquito responses, but the magnitude and time-response of such a force is currently unknown and an area for future work. Regardless of active contribution by legs to slow the mosquito, a passive model well-describes mosquito landing.
The spread posture of mosquito legs during flight (Fig. 1a), the same as upon landing approach, may serve a purpose beyond the previously proposed drag reduction benefits22. The oblique angle between the two forward tarsi, \(\theta _\text {legs}\), ensures that approach angles \(\alpha \lesssim 60^\circ\) toward a vertical surface result in the contact of both forward tarsi. The engagement of the tarsi closest to the substrate induces body rotation to produce foreleg-substrate contact within 8.2 ms. The pliability of a proboscis to absorb impact energy is meager in comparison to the complementary work of legs and wings, and does not obstruct the foreleg tarsi from contacting the surface. The low critical force for proboscis buckling, \(P_{cr}\), allows the mosquito proboscis to collapse in the tangential direction at velocities well below the average value of \(v_\text {n}\).
We cannot confirm landings onto hosts are representative of those captured in this study, which may be described as controlled crashing. Mosquitoes use a variety of thermal, olfactory, and self-induced airflow cues in addition to vision to track their hosts50,57, but it is unclear how non-visual cues aid in clandestine landing. Mosquitoes are also nocturnal, avoiding obstacles invisible to their compound eyes58. We have witnessed activity in response to human attractants to be rather uncontrolled crashes when mosquitoes probe nets for passage19, suggesting such behavior has no landing intent. Mosquitoes are likewise more qualitatively attracted to purple than the polished and translucent acrylic trialed in preliminary experiments, and previous literature suggests they can easily distinguish solid colors from patterns23,26,34,35. The 40-mm high purple landing strip should stand out against its background and change in size as the mosquito approaches. If host landings differ from those on our surface, we expect they produce smaller substrate forces than we calculate as mosquitoes more adequately prepare for impact.
Conclusion
In this study we find Ae. aegypti mosquitoes experience bouncing when engaging surfaces to disperse in-flight momentum. In the first bounce, a mosquito will decrease its impact velocity by approximately 50%, and passively rotate its body, by virtue of its in-flight posture, to engage both pairs of fore- and mid-legs. Landings occur in approximately 100 ms from first contact to wing retraction, and are accompanied by proboscis deflection, which crumples as mosquitoes strike surfaces at an average normal-to-substrate speed of 0.24 m/s. The proboscis is able to absorb up to \(5.4\%\) of the mosquitoes’ initial kinetic energy. Thus, wing aerodynamics and leg compression are the primary mechanisms for kinetic energy dissipation. By treating the mosquito as a simple mass-spring-damper, we find a damping ratio of \(0.36 \pm 0.10\), indicating mosquitoes behave as an underdamped system when engaging a surface, explaining their propensity for bouncing after their initial, and occasionally, subsequent impacts. Free vibration analysis and the assumption of uniform load distribution among both forelegs indicates landings with normal-to-substrate speeds below 0.42 m/s are undetectable by humans. The landing force of the average mosquito in our study is approximately 40 \(\upmu\)N corresponding to an impact velocity of 0.24 m/s.
Data availability
Raw experimental videos and data are available in perpetuity via Open Science Framework: https://osf.io/9wkuj/.
References
van Veen, W. G., van Leeuwen, J. L. & Muijres, F. T. Malaria mosquitoes use leg push-off forces to control body pitch during take-off. J. Exp. Zool. Part A Ecol. Integr. Physiol. 333, 38–49 (2019).
Smith, N. M., Clayton, G. V., Khan, H. A. & Dickerson, A. K. Mosquitoes modulate leg dynamics at takeoff to accommodate surface roughness. Bioinspiration Biomim. 14, 016007 (2018).
Muijres, F. et al. Escaping blood-fed malaria mosquitoes minimize tactile detection without compromising on take-off speed. J. Exp. Biol. 220, 3751–3762 (2017).
Bomphrey, R. J., Nakata, T., Phillips, N. & Walker, S. M. Smart wing rotation and trailing-edge vortices enable high frequency mosquito flight. Nature 544, 92 (2017).
Bomphrey, R. J., Nakata, T., Henningsson, P. & Lin, H.-T. Flight of the dragonflies and damselflies. Philos. Trans. R. Soc. B Biol. Sci. 371, 20150389 (2016).
Ristroph, L., Bergou, A. J., Guckenheimer, J., Wang, Z. J. & Cohen, I. Paddling mode of forward flight in insects. Phys. Rev. Lett. 106, 178103 (2011).
Balebail, S., Raja, S. K. & Sane, S. P. Landing maneuvers of houseflies on vertical and inverted surfaces. PLoS ONE 14, e0219861 (2019).
Shen, C. & Sun, M. Wing and body kinematics measurement and force analyses of landing in fruit flies. Bioinspiration Biomim. 13, 016004 (2017).
Baird, E., Boeddeker, N., Ibbotson, M. R. & Srinivasan, M. V. A universal strategy for visually guided landing. Proc. Natl. Acad. Sci. 110, 18686–18691 (2013).
Parker, J. E. et al. Infrared video tracking of anopheles gambiae at insecticide-treated bed nets reveals rapid decisive impact after brief localised net contact. Sci. Rep. 5, 13392 (2015).
Wagner, H. Flow-field variables trigger landing in flies. Nature 297, 147 (1982).
Srinivasan, M., Zhang, S., Lehrer, M. & Collett, T. Honeybee navigation en route to the goal: visual flight control and odometry. J. Exp. Biol. 199, 237–244 (1996).
Cardé, R. T. et al. Host finding by female mosquitoes: mechanisms of orientation to host odours and other cues. Olfaction Vector-Host Interact. 2010, 115–142 (2010).
Altshuler, D. L. & Srinivasan, M. V. Comparison of visually guided flight in insects and birds. Front. Neurosci. 12, 157 (2018).
Danilovich, S. et al. Bats regulate biosonar based on the availability of visual information. Curr. Biol. 25, R1124–R1125 (2015).
Norberg, U. M. & Rayner, J. M. Ecological morphology and flight in bats (mammalia; chiroptera): wing adaptations, flight performance, foraging strategy and echolocation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 316, 335–427 (1987).
Srinivasan, M. V., Zhang, S.-W., Chahl, J. S., Barth, E. & Venkatesh, S. How honeybees make grazing landings on flat surfaces. Biol. Cybern. 83, 171–183 (2000).
De Jong, R. & Knols, B. G. Selection of biting sites by mosquitoes. In Olfaction in Mosquitoes–Host Interactions. Ciba Fundation Symposium, Vol. 200, 89–103 (1996)
Dickerson, A. K., Olvera, A. & Luc, Y. Void entry by aedes aegypti (diptera: Culicidae) mosquitoes is lower than would be expected by a randomized search. J. Insect Sci. 18, 9 (2018).
Dickerson, A. K., Shankles, P. G., Berry, B. E. Jr. & Hu, D. L. Fog and dense gas disrupt mosquito flight due to increased aerodynamic drag on halteres. J. Fluids Struct. 55, 451–462 (2015).
Saraf, N., Villegas, M., Willenberg, B. J. & Seal, S. Multiplex viral detection platform based on a aptamers-integrated microfluidic channel. ACS Omega 4, 2234–2240 (2019).
Christophers, S. R. Aedes aegypti: the yellow fever mosquito. CUP Archive (1960).
Parker, H. B., Beyer, G. E. & Pothier, O. L. Report of the working party i, yellow fever institute: a study of the etiology of yellow fever. Yellow Fever Institute Bulletin (1903).
Chen, Y. et al. Controlled flight of a microrobot powered by soft artificial muscles. Nature 575, 324–329 (2019).
Sutcliffe, J. F. Sensory bases of attractancy: morphology of mosquito olfactory sensilla-a review. J. Am. Mosquito Control Assoc. 10, 309 (1994).
Peña Torres, J., Navarro Aranda, M., Parra Moreno, H. J. & Duque Luna, J. E. Design and construction of a trap for the surveillance of Aedes (Stegomyia) aegypti (Diptera: Culicidae). Revista de la Universidad Industrial de Santander. Salud 48, 285–294. ISSN 0121-0807 (2016).
Bernáth, B., Anstett, V. & Guerin, P. M. Anopheles gambiae females readily learn to associate complex visual cues with the quality of sugar sources. J. Insect Physiol. 95, 8–16. https://doi.org/10.1016/j.jinsphys.2016.08.011 (2016).
Hoel, D. F. et al. Efficacy of ovitrap colors and patterns for attracting aedes albopictus at suburban field sites in north-central florida. J. Am. Mosquito Control Assoc. 27, 245–251. https://doi.org/10.2987/11-6121.1 (2011).
Gilbert, I. et al. Influence of surface color on mosquito landing rates. J. Econ. Entomol. 50, 678–680 (1957).
Kelber, A. & Henze, M. J. Colour vision: parallel pathways intersect in drosophila. Curr. Biol. 23, R1043–R1045. https://doi.org/10.1016/j.cub.2013.10.025 (2013) (ISSN 0960-9822).
Guo, A., Gong, Z., Li, H., Li, Y., Liu, L., Liu, Q., Lu, H., Pan, Y., Ren, Q., Wu, Z. et al. Vision, Memory, and Cognition in Drosophila A2, pp. 483–503. Oxford: Academic Press. ISBN 978-0-12-805291-4. https://doi.org/10.1016/B978-0-12-809324-5.21029-8 (2017).
Alonso, W. J., Wyatt, T. D. & Kelly, D. W. Are vectors able to learn about their hosts? A case study with aedes aegypti mosquitoes. Memórias do Instituto Oswaldo Cruz 98, 665–672 (2003) (ISSN 0074-0276).
Ernst, R. & Heisenberg, M. The memory template in drosophila pattern vision at the flight simulator. Vis. Res. 39, 3920–3933. https://doi.org/10.1016/S0042-6989(99)00114-5 (1999) (ISSN 0042-6989).
Muir, L. E., Thorne, M. J. & Kay, B. H. Aedes aegypti (diptera: Culicidae) vision: spectral sensitivity and other perceptual parameters of the female eye. J. Med. Entomol. 29, 278–281 (1992) (ISSN 0022-2585).
Muir, L. E., Kay, B. H. & Thorne, M. J. Aedes aegypti (diptera: Culicidae) vision: response to stimuli from the optical environment. J. Med. Entomol. 29, 445–450 (1992) (ISSN 1938-2928).
Horridge, G. A. Insects which turn and look. Endeavour 1, 7–17 (1977).
Srinivasan, M. V. Distance perception in insects. Curr. Dir. Psychol. Sci. 1, 22–26 (1992).
Evangelista, C., Kraft, P., Dacke, M., Reinhard, J. & Srinivasan, M. V. The moment before touchdown: landing manoeuvres of the honeybee apis mellifera. J. Exp. Biol. 213, 262–270 (2010).
Zhao, J., Huang, H. & Yan, S. Honey bees (apis mellifera ligustica) swing abdomen to dissipate residual flying energy landing on a wall. J. Appl. Phys. 121, 094702 (2017).
Pfaff, M. & Varjú, D. Mechanisms of visual distance perception in the hawk moth macroglossum-stellatarum. Zoologische Jahrbucher-Abteilung Fur Allgemeine Zoologie Und Physiologie Der Tiere 95, 315–321 (1991).
Wagner, H. Flight performance and visual control of flight of the free-flying housefly (Musca domestica L.) II. Pursuit of targets. Philos. Trans. R. Soc. Lond. B Biol. Sci. 312, 553–579 (1986).
Liu, P., Sane, S. P., Mongeau, J.-M., Zhao, J. & Cheng, B. Flies land upside down on a ceiling using rapid visually mediated rotational maneuvers. Sci. Adv. 5, 1877 (2019).
Yao, J. & Yeo, K. Free hovering of hummingbird hawkmoth and effects of wing mass and wing elevation. Comput. Fluids 186, 99–127 (2019).
Dickinson, M. H. & Götz, K. G. The wake dynamics and flight forces of the fruit fly drosophila melanogaster. J. Exp. Biol. 199, 2085–2104 (1996).
Ristroph, L. et al. Discovering the flight autostabilizer of fruit flies by inducing aerial stumbles. Proc. Natl. Acad. Sci. 107, 4820–4824 (2010).
Dickerson, A. K., Shankles, P. G., Madhavan, N. M. & Hu, D. L. Mosquitoes survive raindrop collisions by virtue of their low mass. Proc. Natl. Acad. Sci. 109, 9822–9827 (2012).
Li, L. et al. The functional organization of cutaneous low-threshold mechanosensory neurons. Cell 147, 1615–1627 (2011).
Bosak, A. et al. Aptamer-gold nanoparticle conjugates for the colorimetric detection of arboviruses and vector mosquito species. RSC Adv. 9, 23752–23763 (2019).
Hedrick, T. L. Software techniques for two-and three-dimensional kinematic measurements of biological and biomimetic systems. Bioinspiration Biomim. 3, 034001 (2008).
Nakata, T. et al. Aerodynamic imaging by mosquitoes inspires a surface detector for autonomous flying vehicles. Science 368, 634–637 (2020).
Xiong, J. et al. Bending behavior of lightweight sandwich-walled shells with pyramidal truss cores. Compos. Struct. 116, 793–804 (2014).
Xiong, J. et al. Sandwich-walled cylindrical shells with lightweight metallic lattice truss cores and carbon fiber-reinforced composite face sheets. Compos. Part A Appl. Sci. Manuf. 56, 226–238 (2014).
Vinauger, C., Lutz, E. K. & Riffell, J. A. Olfactory learning and memory in the disease vector mosquito Aedes aegypti. J. Exp. Biol. 217, 2321–2330 (2014).
Dekker, T. & Cardé, R. T. Moment-to-moment flight manoeuvres of the female yellow fever mosquito (Aedes aegypti L.) in response to plumes of carbon dioxide and human skin odour. J. Exp. Biol. 214, 3480–3494 (2011).
Beeuwkes, J., Spitzen, J., Spoor, C., Van Leeuwen, J. & Takken, W. 3-d flight behaviour of the malaria mosquito Anopheles gambiae ss inside an odour plume. Proc. Neth. Entomol. Soc. Meet 19, 137–146 (2008).
Dickerson, A. K. & Hu, D. L. Mosquitoes actively remove drops deposited by fog and dew (2014).
van Breugel, F., Riffell, J., Fairhall, A. & Dickinson, M. H. Mosquitoes use vision to associate odor plumes with thermal targets. Curr. Biol. 25, 2123–2129 (2015).
Hawkes, F. & Gibson, G. Seeing is believing: the nocturnal malarial mosquito Anopheles coluzzii responds to visual host-cues when odour indicates a host is nearby. Parasites Vectors 9, 320 (2016).
Acknowledgements
Support for this project was provided in part by the University of Central Florida and a grant from the Florida Department of Agriculture and Consumer Services (FDACS), Contract #026399 (B.J.W.-PI and A.D.). We thank Dr. Daniel Kline (USDA-ARS-CMAVE) for mosquito eggs, and Mrs. Alicia Willenberg for rearing mosquitoes. We also thank Kylie Heckman, Alexis Khalil, and Alexander D’Angelo for experimental contributions, Dr. Jeffrey Kauffman for aid with vibration analysis, and Dr. Ranajay Ghosh for assistance with buckling calculations.
Author information
Authors and Affiliations
Contributions
N.S. and J.B. performed experiments and analyzed data. N.S. prepared all figures. M.D. and B.J.W. reared mosquitoes. N.S., J.B., M.D., B.J.W., and A.D. composed and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Smith, N.M., Balsalobre, J.B., Doshi, M. et al. Landing mosquitoes bounce when engaging a substrate. Sci Rep 10, 15744 (2020). https://doi.org/10.1038/s41598-020-72462-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-72462-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.