Introduction

In the search for interesting metallic states in quantum materials, controlling magnetic orientation, fluctuations, and their interaction with conduction electrons has been of utmost importance. Consequent exotic phases are rich, ranging from unconventional superconductivity1,2,3,4 to giant magneto-transport effects, including metal-to-insulator transition5, magnetically driven 2D confinement6, and exotic Hall effects7,8,9,10,11,12,13,14. One of the most important recent challenges within this field is exploring the exotic magnetic metallic state in van del Waals (vdW) coupled materials15,16,17,18,19,20,21. A missing but crucial component in this challenge is establishing various approaches to controlling the interaction between magnetism and conduction and the mechanism by which they operate.

CeTe3 provides a unique platform to investigate the itinerant magnetism in a van der Waals (vdW) coupled metal22,23,24. The crystal structure of CeTe3 features a square net of Te0.5− and rock-salt type layer of Ce3+ and Te2− (Fig. 1a), combined to realize a highly two-dimensional vdW motif21,25. The conduction band mainly originates from the Te0.5− square net; Ce3+ is responsible for magnetism. Strong nesting of the Fermi surface derived from the square net Te sheet causes a 1D-like charge density wave (CDW) transition below 400 K26,27,28,29,30, whose temperature scale is well separated from the much lower magnetic transition temperature. Based on previous studies23,31, the magnetic moment of CeTe3 can be described as a pseudo spin 1/2 system with strongly easy-plane (XY) character, and long range antiferromagnetic order along the easy-plane is observed below 1.3 K.

Figure 1
figure 1

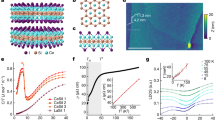
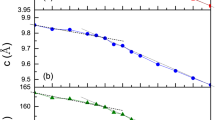
Systematic change of chemical pressure by iso-valent elemental substitution in a vdW coupled material Ce(SexTe1−x)Te2. (a) Crystal structures of CeTe3 (left) and CeSeTe2 (right). Substituted Se atoms enter the magnetic blocking layer selectively. The typical picture of single crystals and the definition of crystallographic directions are also shown. (b) Doping dependence of characteristic X-ray diffraction (XRD) patterns near the (0 8 0) peak for Ce(SexTe1−x)Te2. (c) The out of plane lattice constant b as a function of doping x determined from energy dispersive X-ray spectrometry (EDX). This relation was obtained by performing both XRD and EDX on individual crystal flakes.

Full size image

Recently, CeSeTe2 has been identified as a compound closely related to CeTe3. In CeSeTe2, Se2− selectively substitutes into Te2− sites in CeTe332,33. Consistent with the chemical and structural similarity of CeSeTe2 to CeTe3 (Fig. 1a), a CDW transition and strongly easy-plane- like magnetism in the paramagnetic regime are observed in both materials31. In CeSeTe2 however, the reported magnetism in the ordered state is consistent with a collinear structure pointing in the out-of-plane direction31, which is strongly unfavorable in the paramagnetic state. Thus, by defining the magnetic hard and easy axis/plane of the system based on its paramagnetic state, surprising hard-axis ordering is suggested to emerge in CeSeTe2 below the antiferromagnetic phase transition. Despite this unusual direction of magnetic moment in the ordered state, no detailed measurements have been performed so far to elucidate the underlying mechanism.

To understand the origin of this peculiar hard-axis ordering, here we studied the effect of Se doping systematically through magnetization and heat capacity measurement of Ce(SexTe1−x)Te2. We confirmed that addition of Se applies chemical pressure to Ce3+, which results in exotic reorientation of the magnetic moment through enhanced quantum fluctuation. In this report, we present that the presence of hard-axis ordering is representative of the fermionic order by disorder process, in which a seemingly unstable direction is stabilized through itinerant energy gain.

Results

Crystal growth of Ce(SexTe1−x)Te2

Single crystals of Ce(SexTe1−x)Te2 were grown via the flux method (See method for detail). This formula represents that Se2− selectively replaces Te2− in the magnetic blocking layer (Fig. 1a). Thus, Se2− doping connects the two isostructural systems Ce3+ (Te2−)(Te0.5−)2 and Ce3+ (Se2−) (Te0.5−)2. Since the ionic radii of Se2− and Te2− are 1.98 Å and 2.21 Å, respectively34, systematic control of chemical pressure becomes possible in Ce(SexTe1−x)Te2 through variation of the doping ratio. The single crystals of Ce(SexTe1−x)Te2 present a plate-like morphology with shiny surfaces, reflecting the vdW coupling nature in our system (Fig. 1a). Figure 1b shows the doping evolution of the X-ray diffraction (XRD) pattern around the (080) peak. Figure 1c shows the relationship of the lattice constant along the out-of-plane b axis and the Se/Te ratio x as determined by XRD and energy dispersive X-ray spectrometry (EDX), respectively. As predicted by Vegard’s law, the monotonic linear behavior of the shrinkage of lattice constant with doping suggests the systematic replacement of smaller ionic radii Se2− into the larger ionic radii Te2− sites. Similar monotonic shrinkage of the out of plane lattice constant by doping with elements with smaller ionic radii is also seen in another vdW misfit compounds such as Bi-based cuprates34. In this study, using the obtained linear function, we calculated x from the out-of-plane lattice constant of the crystal flakes used for heat capacity and magnetic measurements.

Magnetic order in CeSeTe2 and CeTe3

We first present a significant difference in the magnetism and heat capacity behavior of CeTe3 (Fig. 2a) and CeSeTe2 (Fig. 2b), despite the common easy-plane feature in the paramagnetic regime. In Fig. 2a,b, magnetic susceptibility χ(T) and heat capacity C(T) are shown on the left and right axes, respectively. For the parent compound CeTe3, we see two characteristic antiferromagnetism related transition temperatures TN1 and TN2. Only a broad peak is observed in C(T) around TN1 while around TN2 a sharp peak in C(T) accompanies stronger suppression of χ(T) along the in-plane (blue and red curves) than the out-of-plane (greed curve) direction. On the other hand, the doped system CeSeTe2 features a single antiferromagnetic transition with a sharp peak at TN3 in C(T) that accompanies stronger suppression of χ(T) along the out-of-plane (green curve) than the in-plane (blue and red curves) directions. Therefore, at the lowest temperature, the Néel vector points along the easy plane in CeTe3, whereas it points along the hard axis in CeSeTe2. This striking contrast is also evident from the suppression of susceptibility and spin flip and flop transitions (Fig. 2c,d) since they should appear along the Néel vector. Figure 2e is the experimentally determined magnetic hard axis and easy plane together with crystal axes. These directions are the same are the same for all samples shown in this study.

Figure 2
figure 2

Magnetism and heat capacity characterization for CeTe3 and CeSeTe2 samples. (a,b) Temperature dependence of the magnetic susceptibility (right axis) for (a) CeTe3 and (b) CeSeTe2 with applying external field H = 0.1 T. On the right axis, temperature dependence of the heat capacity C(T) is also shown. In (a) and (b), there is slight difference in transition temperature since different samples were used for magnetic and heat capacity measurements. (c,d) Magnetic field dependence of the magnetization for (c) CeTe3 and (d) CeSeTe2 at T = 0.5 K. Cartoons for the magnetization process with spin-flop along easy plane and spin-flip along hard axis are shown in (c) and (d), respectively. The red, blue, and green data shown in (a–d) are obtained for H // a, H // c, and H // b, respectively. (e) The experimentally determined magnetic hard axis and easy plane together with crystal axes. These crystallographic and magnetic directions are the same for all samples shown in this study.

Full size image

Quasi two-dimensional magnetism of CeSeTe2 and CeTe3

The ordering phenomena in Ce(SexTe1−x)Te2 based on localized spin picture are briefly discussed before we emphasize the importance of itinerancy. The magnetism of CeTe3 and CeSeTe2 is supposed to originate from highly two-dimensional interactions with XY-like and Ising-like anisotropy, respectively. In CeTe3, the successive phase transitions associated with TN1 and TN2 are reminiscent of the 2D XY model perturbed by weak in-plane anisotropy35. While two-dimensional XY-like interactions can support only quasi long-range order at a finite temperature, genuine long-range order can appear by nearly fourfold symmetric anisotropies at a lower temperature. This picture is presumably captured by the broad and sharp peaks TN1 and TN2, respectively. In contrast, Ising-type long-range-order in CeSeTe2 can appear by breaking discrete Ising symmetry; here in-plane anisotropy plays no role in the magnetic ordering and a single transition has been observed. The abrupt suppression of χ(T) also reflects on the stability of the Ising-like collinear order. It should be noted that the observed collinear magnetism suggests that the Dzyaloshinski–Moriya (DM) interaction, which favors noncollinear spin arrangement regardless of anisotropy of the g factor, should play a minor role in the emergence of hard axis magnetic order. At this stage, it remains unclear why the effective interaction becomes Ising-like by doping even though the paramagnetic susceptibility remains XY-like. As we discuss hereafter, beyond the localized magnetic picture, kinetic energy gain plays a crucial role in explaining an essential part of our experimental observation.

Magnetic fluctuation of Ce(SexTe1−x)Te2

If the ordering direction of CeSeTe2 is actually unfavorable, we should observe self-consistent consequences of enlarged quantum fluctuation. To check this, we investigated the systematic doping dependence of the magnetic fluctuation of Ce(SexTe1−x)Te2. 4f-electron derived entropy S(T) is estimated and plotted in Fig. 3a–f (right axis) based on the formula \(S(T) = \int_{0}^{T} {\frac{{C_{f} }}{T}dT}\). Here, Cf(T) is the heat capacity from the 4f electron contribution (See method for detail). We further calculate magnetic entropy Sm for S(TN1) and S(TN3) as x < 0.54 and x > 0.54, respectively. Based on a fully localized picture, Sm should asymptotically approach Rln2 (~ 5.76 JK−1 mol−1). This value is simply derived from the ground state doublet of Ce3+ ions under the crystalline electric field. Thus, 1 − Sm/Rln2 can be taken as the measure of the strength of magnetic fluctuation for a given magnetic order.

Figure 3
figure 3

Doping and temperature dependence of heat capacity C(T) of Ce(SexTe1−x)Te2. (a–f) Temperature dependence of the heat capacity (circles; left axis) and magnetic entropy (solid line; right axis) of (a) x = 0, (b) x = 0.27, (c) x = 0.45, (d) x = 0.60, (e) x = 0.87, (f) x = 0.96. The purple color represents data obtained from samples with easy plane antiferromagnetism (AF), and the orange represents those with hard axis AF. In (a), the value Rln2 (~ 5.76 JK−1 mol−1) is shown with a broken line. This value is the calculated magnetic entropy from the ground state doublet of Ce3+ ions under the crystalline electric field.

Full size image

Evolution of magnetic fluctuation by doping

By constructing a phase diagram, a correlation exists between enhanced magnetic fluctuation and emergent hard-axis moment. Figure 4a represents the phase diagram with three characteristic temperatures (left axis) together with 1 − Sm/Rln2 (right axis). With increasing doping x, TN1 and TN2 are systematically decreased for x < 0.54. Above x = 0.54, we see only one transition temperature TN3. Therefore, combining magnetic measurements for CeTe3 (Fig. 2a) and CeSeTe2 (Fig. 2b), a first-order magnetic transition is expected to exist near x = 0.54, across which the direction of magnetic moment abruptly changes from the easy plane to the hard axis. The enhancement of 1 − Sm/Rln2 towards the first-order transition point is partly due to the chemical disorder effect since chemical entropy naturally reaches a maximum at x = 0.5 in our alloyed system. As a consequence, chemical disorder may contribute to a slight increase in 1 − Sm/Rln2 with doping levels above x = 0.54 (Fig. 4a). However, we emphasize that the values 1 − Sm/Rln2 for two nearly stoichiometric samples with x = 0 and x = 0.96 are 0.25 and 0.36, respectively. Based on these values, the magnetic fluctuation of stoichiometric CeSeTe2 is expected to be ~ 1.4 times larger than that of the parent compound CeTe3. Therefore, the key feature to be captured in the phase diagram is an emergent hard-axis moment with a monotonic enhancement of magnetic fluctuation.

Figure 4
figure 4

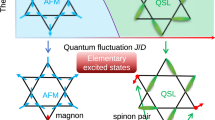
The phase diagram representing magnetic rotation associated with enhanced quantum fluctuation. (a) Temperature-doping phase diagram of Ce(SexTe1−x)Te2 for three successive magnetic transition temperatures (TN1, TN2, and TN3) and magnetic entropies 1 − Sm/Rln2. The data used in this phase diagram are from specific heat measurements. (b) Schematic drawing of Fermionic order by disorder. The magnetic moment lies in the easy axis (plane) and is reduced with enhanced quantum fluctuation for x < 0.54. Whereas with enhanced fluctuation the magnetic moment moves to lie along the hard axis (x > 0.54) and expresses enhanced precession as for an Ising-like moment. The kinetic energy gain with enhanced magnetic fluctuation is represented as a change from localized wave packet (left) to delocalized wave packet (right). As a detailed spin structure for antiferromagnetism within this compound is not totally clear, ferromagnetically aligned spins within single Ce square lattice sheet along ac plane (see Figs. 1a, 2a) are drawn for clarity.

Full size image

Discussion

We propose the possible mechanism leading to emergent hard axis ordering in terms of fermionic order by disorder in itinerant systems36,37. Our observation is that the change in chemical pressure enhanced the magnetic quantum fluctuation and altered the direction of Néel vector to the apparent “hard axis”. This implies that magnetic quantum fluctuation itself drives the hard-axis ordering as in the case of “order by disorder” in frustrated magnets38. The relevant quantum fluctuation is unlikely to be Kondo screening in our case because a similar magnitude of saturated magnetic moment along the easy-axis with doping was observed experimentally (Fig. 2c,d). Instead, we propose that the enhanced magnetic fluctuation is a spin-wave excitation, which is the primary fluctuation from the magnetically ordered state. An important point to note is that the spin-wave excitation is a transverse fluctuation. Since the transverse direction from the hard axis is on the easy plane, hard-axis order can fluctuate more easily than easy-plane order. We surmise that the hard-axis order becomes favorable when chemical pressure further enhances quantum fluctuation of localized spin through Kondo coupling.

Compared to localized frustrated magnets, fermionic order by disorder requires kinetic energy gain of electrons in addition to transverse spin fluctuation (Fig. 4b). Such physics is directly captured by investigating electronic quasiparticle band deformation to lower the total energy of the system. This concept is consistent with the Fermionic order-by-disorder process, as predicted theoretically36,37. Regardless of theoretical proposals, however, experimental direct visualization of quasi-particle band deformation has been missing due to the lack of proper materials to investigate with high resolution. Compared with materials in existing studies such as YbRh2Si2, YbNi4P2, and CeT2Al10 (T = Ru, Os)39,40,41,42,43,44,45 the intrinsically cleavable nature and simple composite structure of our vdW material offers an excellent platform for unveiling rich quasiparticle band deformation using surface sensitive spectroscopies with changing external magnetic field, its orientation and temperature. In addition, inherent applicability of advanced exfoliation techniques46 will further enrich future challenges in searching for novel quantum phenomena.

In summary, we show magnetic fluctuation driven unusual magnetic rotation from the usual easy plane to unusual hard axis moment across the magnetic phase transition. As far as we recognize, this is the first report of the order-by-disorder process in fermionic system in a vdW coupled antiferromagnet, which opens various unique research directions for the future.

Methods

Synthesis of monocrystalline Ce(SexTe1−x)Te2

Single crystals of Ce(SexTe1−x)Te2 are grown using self-flux method. The mixture of the elemental powder of cerium (99.9%), selenium (99.999%), and tellurium (99.999%) in a molar ratio of 1:2x/3:40-2x/3 was placed inside the alumina crucible and sealed in an evacuated quartz tube. The ampoule was heated to 900 °C at a rate of 75 °C/hour, kept at 900 °C for 24 h, and then slowly cooled down to 550 °C at a rate of 2 °C/hour followed by centrifugation to remove crystals from the melt.

Magnetization and heat capacity measurement

DC magnetization and heat capacity were measured using a Magnetic Property Measurement System (Quantum Design) with a 3He insert47 and a Physical Property Measurement System PPMS (Quantum Design) with a 3He insert, respectively.

Estimation of magnetic heat capacity

We extracted the magnetic fluctuation strength from heat capacity C(T) (Fig. 3a–f left axis) based on the method described as follows. To obtain the 4f electron contribution Cf(T), first we subtract C(T) of LaTe3 from that of Ce(SexTe1−x)Te2. This subtraction relies on the assumption that phonon and electronic contributions not arising from the 4f electrons are the same between LaTe3 and Ce(SexTe1−x)Te2 (see supplemental information). From comparison, the specific heat is dominated by 4f electron derived signal, and phonon subtraction is a minor correction within the main purpose of this study. Using the obtained Cf(T), Here, we set Cf(0) = 0 to calculate S(T). This assumption is physically not exactly accurate since heat capacity is finite due to itinerant 4f-electron nature; It does not however have a large impact within the purpose of extracting magnetic entropy since electronic contribution relative to magnetic contribution is much lower.