Abstract
In this paper an automatic adaptive antenna impedance tuning algorithm is presented that is based on quantum inspired genetic optimization technique. The proposed automatic quantum genetic algorithm (AQGA) is used to find the optimum solution for a low-pass passive T-impedance matching LC-network inserted between an RF transceiver and its antenna. Results of the AQGA tuning method are presented for applications across 1.4 to 5 GHz (satellite services, LTE networks, radar systems, and WiFi bands). Compared to existing genetic algorithm-based tuning techniques the proposed algorithm converges much faster to provide a solution. At 1.4, 2.3, 3.4, 4.0, and 5.0 GHz bands the proposed AQGA is on average 75%, 49.2%, 64.9%, 54.7%, and 52.5% faster than conventional genetic algorithms, respectively. The results reveal the proposed AQGA is feasible for real-time application in RF-front-end systems.
Similar content being viewed by others
Introduction
Antennas provide an interface with the propagating medium and therefore are essential components in wireless communication systems. There is a great demand for a single antenna that can operate efficiently over wide frequency band to accommodate software-defined multi-standard functionality1. Conventional wideband antennas for wireless systems are designed to perform satisfactorily, i.e. non-optimum, as the feed-point impedance cannot be matched properly over its operating band. Hence, at the transmitter the efficiency of the high power-amplifier is sub-optimum or at the receiver the low-noise amplifier performance is sub-optimum. To circumvent this issue an impedance matching network needs to be inserted between the antenna and transceiver. Impedance of antennas however can vary significantly with frequency as well as with operating conditions that can result in great impedance variations caused by various factors such as the proximity of a cellular phone to the user’s ear2. The use of a single impedance matching network with fixed LC component values is therefore unsuitable for realizing accurate matching over a wide frequency range. To realize optimum performance in terms of power and efficiency, it is therefore necessary to utilize an automatically tuneable impedance matching network that can dynamically control the antenna’s impedance, frequency band or operating conditions3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21. As yet automatically tuneable impedance matching networks are unsuitable for integration in wireless systems because tuning takes too long for practical applications.
Existing impedance tuning algorithms employ a step-by-step methodology where the passive tuning network is modified progressively until the required impedance match goal is realized3,22. Such gradient-based algorithms are computationally intensive because arrival at a solution involves calculation of matrix inversion that can often converge to localised optima8,19. Other algorithms investigated to date to circumvent such issues include (i) genetic algorithms (GA) that use non-gradient and global evolution optimising approaches3,23, and (ii) quantum genetic algorithms (QGA) that exploit the laws of quantum mechanics in order to perform efficient computation. Genetic algorithms are essentially adaptive search algorithms based on the evolutionary ideas by Charles Darwin of natural selection and genetics. These search algorithms operate on a set of elements, referred to as population, that evolves by means of crossover and mutation, towards a maximum of the fitness function. QGA have shown to be computationally efficient at solving problems like factorization24 or searching in an unstructured database25.
Taking advantage of the quantum to efficiently speed-up classical computation, the QGA outperforms the conventional genetic algorithms (CGA) when the fitness function is varying between genetic iterations. QGA updates the colony by combining quantum bit (qubit) coding with binary coding. It is a kind of efficient parallel algorithm. Qubits are exploited not only to represent the population, but also to perform fitness evaluation and selection. QGA uses the whole population at each genetic step, and in this sense, it can be considered to be a ‘global search’ algorithm.
Conventional genetic algorithms have been investigated for tuning the impedance of antennas19,20,23 but its use has been limited because of issues with obtaining an optimum goal and being slow. Although automatic genetic algorithm (AGA) is an attractive solution for software-defined transceivers it too faces the challenge of achieving an optimum solution quickly as the input impedance of the matching network is a non-linear function of load impedance. Therefore, a more efficient tuning algorithm is needed. Proposed in this paper is impedance tuning of antennas based on automatic quantum genetic algorithm (AQGA) that has been shown to be computationally efficient compared to CGA25,26,27,28,29,30 where the fitness function various continuously. The proposed AQGA is shown to arrive at an optimum impedance matching solution significantly quicker compared to conventional genetic algorithms. In fact, on average at 1.4 GHz band it is 75% faster,at 2.3 GHz band it is 49.2% faster,at 3.4 GHz band it is 64.9% faster; at 4.0 GHz band it is 54.7% faster; and at 5.0 GHz band it is 52.5% faster.
Automatic antenna tuning system (AATS)
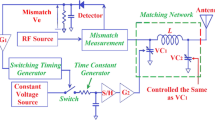
The proposed automatic antenna tuning system is designed to conjugately match the impedance of the antenna with the transmitter’s impedance across the operating frequency band of the wireless system. The AATS, shown in Fig. 1, comprises (i) a tuneable matching network that generates the desired impedance transformation, (ii) an impedance sensor to measure the VSWR at the matching network input; and (iii) a control unit that modifies the impedance of the matching network to the desired impedance based on feedback from the impedance sensor by using the proposed tuning algorithm. The matching system can respond to variations in the antenna impedance affected by changes in its operating conditions.
Impedance matching LC-network
As the antenna impedance is a function of the frequency and operational conditions, therefore the impedance matching network should be capable of being dynamically adaptable. The matching process involves suitably controlling the parameters of the matching network. The low-pass \(\pi\)-type and T-type impedance matching LC-networks are attractive configurations as they enable the use of a broad range of load impedances and harmonic-rejection characteristics4,30.
The proposed low-pass passive T-type impedance matching LC-network, which is located between the transmitter and antenna, is shown in Fig. 2, where \(Z_{source}\) is the source impedance of the transmitter, and \(Z_{Load}\) represents the load impedance. Impedances \(Z_{A}\), \(Z_{B}\) and \(Z_{input}\) are annotated in Fig. 2 at each transformation stage from the load to the source. To realize impedance matching \(Z_{input}\) must equal the real part of the source impedance, \(R_{sousce}\). Hence, the maximum available power transfer to the load and Voltage Standing Wave Ratio (VSWR) can easily be determined from Fig. 2 as following
where \(X_{A} = X_{Load} + \omega L_{2}\)
or
where \(A = \frac{R}{{\left( {1 + \omega CX_{A} } \right)^{2} + \left( {\omega CR_{Load} } \right)^{2} }}\) and \(B = \omega L_{1} + \frac{{X_{A - } \omega C\left( {X_{A}^{2} + R_{Load}^{2} } \right)}}{{\left( {1 + \omega CX_{A} } \right)^{2} + \left( {\omega CR_{Load} } \right)^{2} }}\).
Reflection-coefficient (\(\Gamma_{input}\)) at input of the LC-network is defined by
and
Maximum available power from source is
Power delivered to the LC-network can be derived and is given by
where \(\Gamma_{soarce}\) is reflection-coefficient at the source, and \(Z_{o}\) is the characteristic impedance.
In the proposed T-type impedance matching LC-network the magnitude and range of the reactive components should cover the impedances necessary to match the antenna across the wireless systems operating bandwidth. The reactive components should be controllable to accommodate variations in the antenna’s operating conditions. To implement the tuning requirement an array of digital switches of fixed value reactive component are deployed, as shown in Fig. 3. This arrangement facilitates automatic adjustment of the matching network to meet the matching condition (ideally \(\Gamma_{source} = 0\) and \(VSWR = 1\)) using a tuning algorithm.
Proposed automatic quantum genetic algorithm
Fast tuning algorithm is required for antenna impedance networks especially with changing loads and operational conditions. In the case where many network combinations are possible it is important to have a tuning algorithm that can reduce the number of networks possible. This can be achieved by generating a look-up table of matching networks for various frequencies in the operating range. This approach will facilitate the control system to rapidly select a suitable tuning network as a function of frequency8. The disadvantage of this approach is it’s not able to respond quickly to changes in the antenna’s impedance as a function of time without repeating the whole process again.
Genetic tuning algorithms, however, based on iterations converge on the best impedance networks23,25,26. Such algorithms must initially perform many iterations to arrive at a satisfactory impedance solution with no need for explicit rules. But with continued operation such algorithms achieve matching with fewer iterations. The disadvantage of GA is it requires significant computational time.
It has been shown that AQGA is an efficient algorithm23,27,28,29,30 as it’s (i) less prone to being trapped in a localised optimum solution,(ii) requiring less iteration; and (iii) it converges more rapidly to a final solution. It is for these reasons the tuning mechanism chosen here is based on AQGA.
Representation
AQGA is a quantum inspired genetic algorithm that is based on quantum computation and conventional GA. Its states are a superposition of qubits23,27. A qubit can assume state |0 > or |1 > , or any superposition of the dual states defined by |\(\delta\) > = \( i\)|0 > + \(j\)|1 > , where parameters \(i\) and \(j\) represent complex numbers indicating the probability-amplitudes of the respective states. For a system of n qubits, the system can exhibit \(2^{n}\) states concurrently. Its representation is given by 4,30
where
One qubit chromosome in Eq. (9) can represent all possible states in the primary stages of evolution, whereas 2n chromosomes are required in a classical system.
For the T-type impedance matching LC-network in Fig. 2, the components (\(L_{1}\), \(L_{2}\), and \(C\)) are coded in the form of Eq. (9). The chromosome \(\left[ {L_{1} ,L_{2} ,C} \right]\) comprises 30-bit qubits, where 10-bit qubits represent each component. The quantum algorithm’s challenge is to determine the minimum list of M items.
Structure of AQGA
The structure of the AQGA for modifying the T-type impedance matching LC-network is thus4,30:
(i) Initialize the binary instants and the quantum population (do this for each generation)
(ii) Compute the fitness of each entity \(P_{Y}^{x}\)
(iii) Categorize the entities related to the fitness amounts and store the best chromosome
(iv) Apply the quantum genetic operators on \(P_{Quantum}^{x}\)and update qubit chromosome applying rotation matrix
The initial component magnitudes of the T-type impedance matching LC-network are achieved from the previous section and are adjusted by random numbers where the magnitudes of the probability amplitudes are selected in a random fashion from the intervals of \(L_{1} , L_{2} \in \left\{ {10^{ - 12} ,10^{ - 6} } \right\}\) and \(C \in \left\{ {10^{ - 14} ,10^{ - 7} } \right\}\). Constituents of the quantum population are represented as
where
\(Q_{y}^{x}\) is the \(l{th}\) qubit size in the \(x{\rm th}\) generation of the \(y{\rm th}\) constituent in the quantum population (\(P_{Y}^{x}\)) and \(m\) is the population size. \(P_{Y}^{x}\) is generated from qubit chromosome \(P_{Quantum}^{x}\), and represented as
where \(Y_{y}^{x}\) is the \(x{\rm th}\) bit of the chromosome.
The quantum matrix is transformed into a binary matrix in the measurement operation. As done in other quantum systems a single solution is extracted from the quantum matrix while preserving all other configurations. The magnitude of the qubit is determined according to its probability pairs \(\left| {i_{y,l}^{x} } \right|^{2}\) and \(\left| {j_{y,l}^{x} } \right|^{2}\). Population of binary entities is built from the quantum population \(P_{Quantum}^{x}\). Each qubit is observed for any destruction in the qubit chromosome. Diversity in population is achieved by generating a random number. |1 > state is recorded whenever the magnitude of the random number is bigger than the corresponding chromosome probability amplitude. If the magnitude of the random number is smaller compared to the corresponding chromosome probability amplitude |0 > state will be observed.
In the evaluation phase the fitness of the current and the best chromosome is given by \(f\left( {CH_{\beta }^{\alpha } } \right)\) and \(f\left( {CH_{best} } \right)\), respectively, where \(CH_{best}\) is the \(\alpha{\rm th}\) bit of the best chromosome. \(f\left( {CH_{best} } \right)\) is obtained from
For the T-type impedance matching LC-network, the population is evaluated by
where \(Z_{input}\) is the population’s actual input impedance, and \(\Gamma_{source}\) is the source’s actual reflection-coefficient. The aim of the tuning algorithm is to determine the values of \(L_{1}\), \(L_{2}\), and \(C\) to meet the matching conditions. This is followed by updating the xth population of qubit chromosomes \(P_{Quantum}^{x}\) by applying quantum rotation.
Qubit chromosome of \(P_{Quantum}^{x}\) with the best fitness is chosen for each binary chromosome \(P_{Y}^{x}\). Then qubit chromosomes are sorted according to the values of the fitness in every iteration executed. To avoid convergence to a local maximum, the selection strategy used here was to extract the optimum and part of "not so good" entities. In this way global optimisation is achieved. A uniform quantum crossover operation is applied thereafter to the chosen entities. This is followed by mutating the probability amplitude of each qubit chromosome to generate new entities. Finally, the quantum chromosome is updated by using quantum rotation. The rotation matrix is represented by
where \(\varphi\) represents the angle of the rotation. The \(l{\rm th}\) qubit in the \(x{\rm th}\) generation is
which is updated as
where \(\varphi_{y,l}^{x}\) is the corresponding rotation angle of \(Q_{y}^{x}\).
where \(\left| {\varphi_{y,l}^{x} } \right|\) is its amplitude and \(d_{y,l}^{x}\) is its sign. \(d_{y,l}^{x}\) is dependent on Ψ = \(i_{y,l}^{x}\). \(j_{y,l}^{x}\). Table 1 shows the relation between the fitness condition \(d_{y,l}^{x}\) and "Ψ", where the mark sensing Ψ > 0 stands Re(Ψ).Im(Ψ) > 0, and Ψ < 0 denotes for Re(Ψ).Im(Ψ) < 0. In case of Ψ = 0, i.e. \(i_{y,l}^{x}\) = 0 or \(j_{y,l}^{x}\) = 0, there are different \(d_{y,l}^{x}\) amounts, whose details are presented in Table 1. The symbolism ‘*’ illustrates arbitrary state, symbol “1” in the columns demonstrates for the clockwise rotation of \(d_{y,l}^{x}\), and “0” in the columns corresponded to \(d_{y,l}^{x}\) indicates that rotation is not accomplished. The rotation operation helps AQGA to converge rapidly to find a solution.
Results and discussions
The proposed automatic quantum GA tuning approach is compared with the conventional GA methodology to verify its effectiveness. It was therefore necessary to extensively simulate both tuning approaches. The tuning times of the algorithms was assessed over 400 simulations to determine the algorithm’s speed in arriving at the optimal solution. The training diagrams of the AQGA tuning approach are shown in Fig. 4 for the following conditions: \(Z_{source}\) = 50 + j30 Ω, \(Z_{Load}\) = 75 + j50 Ω, signal frequency of 5 GHz (WiFi band), and signal amplitude of 1 V. The results shown are a function of size of genetic population, probability of mutation, cross-probability, specific mutation, cross and selection operations. The AQGA tuning was executed many times for various parameter magnitudes. The best and average fitness results in Fig. 4 corresponds to a population size of 100 entities, a mutation probability of 0.5% and a cross-probability of 12.4%. The best entities are chosen by the probability of 85% and the remainders are chosen by the probability of 15%. The algorithm terminated after 750 generations and the optimum solution achieved at this point is applied, which results in \(L_{1}\) = 5.62 nH, \(L_{2}\) = 3.45 nH, and \(C\) = 2.18 pF. The quantum elapsed time is 7.25 s. Figure 4(b) shows the corresponding reflection-coefficient variations with training epochs. Table 2 also gives the different load impedance results at 5 GHz (WiFi band).
In another example, AQGA tuning is applied to source impedance of \(Z_{source}\) = 50 + j30 Ω, load impedance of \(Z_{Load}\) = 75 + j50 Ω, source signal frequency of 3.4 GHz (radar systems), and signal amplitude of 1 V. Computational results in Fig. 5 are for a population size of 100 entities, a mutation probability of 0.6% and a cross-probability of 13.6%. Best entities are chosen by the probability of 87% and the remainders are selected by the probability of 13%. The algorithm terminates after 750 generations and the optimum goal achieved gives \(L_{1}\) = 7.11 nH, \(L_{2}\) = 4.25 nH, and \(C\) = 3.05 pF. The quantum elapsed time is 7.02 s. Table 2 also gives the results for different load impedances at 3.4 GHz (radar systems).
Statistical results of 400 executions for various load impedances applying the proposed AQGA are presented in Table 2 for different frequency bands, i.e. 1.4 GHz (military and satellite services), 2.3 GHz (LTE networks), 3.4 GHz (radar systems), 4.0 GHz (satellite earth stations), and 5.0 GHz (WiFi band), where the relative error in input impedance is defined as
where \(Z_{input}\) is the input impedance determined from the tuning algorithm, and \(Z_{source }\) = 50 + j30 Ω is the source impedance to be matched. As can be seen from Table 2, the errors of the input impedance and VSWR obtained are negligible. Summarized in Table 2 is the results of the training epoch, relative error, and the reflection coefficient for various load impedances at various frequencies.
The conventional GA tuning approach was also carried out for comparison purposes using the same impedance matching network at various frequencies of 1.4 GHz (military and satellite services), 2.3 GHz (LTE networks), 3.4 GHz (radar systems), 4.0 GHz (satellite earth stations), and 5.0 GHz (WiFi band). The numerical results are given in Table 2. It is evident from the table that the proposed AQGA tuning method arrives at the required component value using significantly less iterations in comparison to the CGA tuning method.
The AQGA and CGA tuning algorithms were executed on a Pentium (R) 7 CPU 16 GHz PC. The longest, shortest, and average time for 400 runs for both algorithms are given in Table 3. The proposed AQGA approach obtains the solution much more rapidly compared with the CGA approach.
The proposed approach of single frequency tuning can be applied for tuning a given RF band. This involves first tuning the matching network to the center frequency of the operating band of the system. Component values obtained for other frequencies in the given band are then used to compute the VSWR values. As an example, let’s consider the WiFi band (5,350–5,925 MHz) with a bandwidth of 575 MHz. The T-type impedance matching network is tuned at the WiFi’s centre frequency of 5.63 GHz for source impedance of \(Z_{source}\) = 50 + j30 Ω, load impedance of \(Z_{Load}\) = 75 + j50 Ω, and signal amplitude of 1 V. The algorithm provides impedance matching component values of \(L_{1}\) = 6.50 nH, \(L_{2}\) = 4.36 nH and \(C\) = 2.95 pF. The VSWR as a function of frequency is shown in Fig. 6 by applying these component values. The VSWR varies in a V-shape response across its band between 1.15 and 1.35. This shows the VSWR performance is acceptable over the whole bandwidth from 5,350 to 5,925 MHz after the tuning algorithm converges.
Figure 7 show the VSWR frequency response for a wider RF band defined between 1,400 and 3,400 MHz, i.e. ISM band in which WLAN, Wi-Fi and Bluetooth operate. In this case the VSWR falls in the range between 1.05 and 1.25. This result shows the effectiveness of the proposed algorithm.
In the case for much wider RF bands, the tuning to the band centre may not give the accuracy required. It is therefore proposed to use multiple frequencies for tuning to realize one set of optimum component values that cover the specified frequency band for a pre-set error.
Conclusions
Effectiveness of the proposed automatic quantum genetic algorithm (AQGA) is demonstrated against the conventional genetic algorithm (CGA) to adaptively modify the impedance of the matching network to conjugately match the impedance of the antenna with the transmitter’s impedance across the operating frequency band of the wireless system. Optimum matching solution is reached in a significantly shorter time compared to CGA. The proposed algorithm was applied in several scenarios to tune the T-type impedance matching LC-network at different frequency bands. The results presented verify the effectiveness of the proposed AQGA tuning approach for real-time adaptive antenna tuning.
References
Saidatul, N. A., Soh, P. J., Sun, Y., Lauder, D. & Azremi, A. A. H. Multiband fractal PIFA (planar inverted F antenna) for mobile phones (Proc. IEEE Int. Symp. Wireless Communications Systems, York, 2010).
Boyle, K. R., Yuan, Y. & Ligthart, L. P. Analysis of mobile phone antenna impedance variations with user proximity. IEEE Trans. Antennas Propag. 55(2), 364–372 (2007).
Sun, Y., Moritz, J., & Zhu, X. Adaptive impedance matching and antenna tuning for green software defined and cognitive radio. In Invited Paper in special session on Signal Processing for Software Defined and Cognitive Radio, 54th IEEE Midwest Symposium (Circuits and Systems, Seoul, Korea 2011).
Tan, Y., Yi, R. & Sun, Y. Wideband tuning of impedance matching networks using hierarchical genetic algorithms for multistandard mobile communications. J. Comput. 7(2), 356–361 (2012).
Mileusnic, M., Petrovic, P. & Todorovic, J. Design and implementation of fast antenna tuners for HF radio systems 1722–1725 (ICICS ‘97, Singapore,1997, 3B3.1).
Moritz, J. R., Lauder, D. M. & Sun, Y. Measurement of HF antenna impedances. In IEE Colloquium on Frequency Selection and Management Techniques for HF Communications pp. 141–147 (Ref No. 1999/017, London, 1999).
Ida, I., Takada, J., Toda, T. & Oishi, Y. An adaptive impedance matching system and its application to mobile antennas. Proc. IEEE TENCON 3, 543–546 (2004).
De Mingo, J., Valdovinos, A., Crespo, A., Navarro, D. & Carcia, P. An RF electronically controlled impedance tuning network design and its application to an antenna input impedance automatic matching systems. IEEE Trans. Microw. Theory Tech. 52(2), 489–497 (2004).
Zolomy, A., Mernyei, F., Erdelyi, J., Pardoen, M. & Toth, G. Automatic antenna tuning for RF transmitter IC applying high Q antenna. In IEEE Radio Frequency Integrated Circuits Symposium pp. 501–504 (Paper TU4D-4, 2004).
Meng, F., Bezooijen, A. & Mahmoudi, R. A mismatch detector for adaptive antenna impedance matching. In Proceedings of 36th European Microwave Conference pp. 1457–1460 (Manchester, 2006).
Oh, S.-H., Song, H., Aberle, J. T., Bakkaloglu, B. & Chakrabarti, C. Automatic antenna tuning unit for software-defined and cognitive radio. Wirel. Commun. Mobile Comput. 7, 1103–1115 (2007).
Song, H., Bakkaloglu, B. & Aberle, J. T. A CMOS adaptive-antenna impedance tuning IC operating in the 850 MHz-to-2 GHz band. In IEEE International Solid-State Circuits Conf, Session 22 18–20 (2009).
Chamseddine, A., Haslett, J. W. & Okoniewski, M. CMOS silicon-on-sapphire tunable matching networks. EURASIP J. Wirel. Commun. Netw.. article ID 86531 (2006).
Sjoblom, P. & Sjoland, H. An adaptive impedance tuning CMOS circuit for ISM 2.4-GHz band. IEEE Trans. Circuits Syst. 52(6), 1115–1124 (2005).
Sjoblom, P. & Sjoland, H. Measured CMOS switched high-quality capacitors in a reconfigurable matching network. IEEE Trans. CAS-II 54(10), 858–862 (2007).
Firrao, E. L., Annema, A. J. & Nauta, B. An automatic antenna tuning system using only signal amplitudes. IEEE TCAS-II 55(9), 833–837 (2008).
Van Bezooijen, A. et al. A GSM/EDGE/ WCDMA adaptive series-LC matching network using RF-MEMS switches. IEEE J. Solid-State Circuits 43(10), 2259–2268 (2008).
Van Bezooijen, A., de Jongh, M. A., van Straten, F., Mahmoudi, R. & van Roermund, H.M. Adaptive impedance-matching techniques for controlling L networks. IEEE Trans. Circuits Syst. I, Regul. Pap. 57(2), 495–505 (2010).
Ogawa, K., Takahashi, T., Koyanagi, Y. & Ito, K. Automatic impedance matching of an active helical antenna near a human operator. In Thirty-third European Microwave Confrence 1271–1274 (2003).
Sun, Y. & Lau, W. K. Automatic impedance matching using Genetic Algorithms 31–36 (Proc. IEE Conf. Antennas and Propagation, York, 1999).
Soltani, S., Lotfi, P. & Murch, R. D. Design and optimization of multiport pixel antennas. IEEE Trans. Antennas Propag. 66(4), 2049–2054 (2018).
Elshurafa, A. M. & El-Masry, E. I. Tunable matching networks for future MEMS-based transceivers. Proc. IEEE Int. Symp. Circuits Syst. 4, 457–460 (2004).
Thompson, M. & Fidler, J. K. Application of the genetic algorithm and simulated annealing to LC filter tuning. IEE Proc. Circuits Devices Syst. 148(4), 177–182 (2001).
Shor, P. W. Algorithms for quantum computation: discrete logarithms and factoring. In Proceedings of 35th Annual Symposium Found. Computer Science 124–134 (Los Alamitos, CA, 1994).
Grover, L. K. Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett 79(2), 325–328 (1997).
Han, K. H. & Kim, J. H. Quantum-inspired evolutionary algorithm for a class of combinatorial optimization. IEEE Trans. Evol. Comput. 6(6), 580–592 (2002).
Liu, Q. Y. et al. ‘Design optimization of power transformer based on multilevel genetic algorithm. J. Xi’an Jiaotong Univ. 43(6), 113–117 (2009).
Malossini, A., Blanzieri, E. & Calarco, T. Quantum genetic optimization. IEEE Trans. Evol. Comput. 12(2), 231–241 (2008).
Narayanan, A. & Moore, M. Quantum inspired genetic algorithm. Proc. Int. Conf. Evol. Comput. 61–66 (1996).
Tan, Y., Sun, Y. & Lauder, D. Automatic impedance matching and antenna tuning using quantum genetic algorithms for wireless and mobile communications. IET Microw. Antennas Propag. 7(8), 693–700 (2013).
Acknowledgments
This work is partially supported by RTI2018-095499-B-C31, Funded by Ministerio de Ciencia, Innovación y Universidades, Gobierno de España (MCIU/AEI/FEDER,UE), and innovation programme under grant agreement H2020-MSCA-ITN-2016 SECRET-722424 and the financial support from the UK Engineering and Physical Sciences Research Council (EPSRC) under grant EP/E022936/1.
Author information
Authors and Affiliations
Contributions
Conceptualization, M.A., B.S.V., P.S., C.H.S., R.A.A.-A., F.F., and E.L.; methodology, M.A., B.S.V., F.F., E.L.; software, M.A., P.S., and C.H.S.; validation, M.A., B.S.V., P.S., and C.H.S.; formal analysis, M.A., F.F., and E.L.; investigation, M.A., P.S., C.H.S., and R.A.A.-A.; resources, M.A., B.S.V., P.S., C.H.S., R.A.A.-A., F.F., and E.L.; data curation, M.A., B.S.V., C.H.S., and R.A.A.-A.; writing—original draft preparation, M.A.; writing—review and editing, M.A., B.S.V., P.S., C.H.S., R.A.A.-A., F.F., and E.L.; visualization, M.A., B.S.V., P.S., C.H.S., R.A.A.-A., F.F., and E.L.; supervision, E.L.; project administration, R.A.A.-A., F.F., and E.L.; funding acquisition, R.A.A.-A., F.F, E.L..
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alibakhshikenari, M., Virdee, B.S., Shukla, P. et al. Improved adaptive impedance matching for RF front-end systems of wireless transceivers. Sci Rep 10, 14065 (2020). https://doi.org/10.1038/s41598-020-71056-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-71056-0
This article is cited by
-
RF energy harvesters for wireless sensors, state of the art, future prospects and challenges: a review
Physical and Engineering Sciences in Medicine (2024)
-
Analysis of harmonics and their mitigation for a tuned cylindrical monopole antenna
Sādhanā (2023)
-
A Multi-Band Impedance Matching Strategy Using Lumped Resonant Circuits
Circuits, Systems, and Signal Processing (2023)
-
Dual-functional communication and sensing antenna system
Scientific Reports (2022)
-
A 61.2-dBΩ, 100 Gb/s Ultra-Low Noise Graphene TIA over D-Band Performance for 5G Optical Front-End Receiver
Journal of Infrared, Millimeter, and Terahertz Waves (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.