Abstract
This paper introduces a differential vibrating beam MEMS accelerometer demonstrating excellent long-term stability for applications in gravimetry and seismology. The MEMS gravimeter module demonstrates an output Allan deviation of 9 μGal for a 1000 s integration time, a noise floor of 100 μGal/√Hz, and measurement over the full ±1 g dynamic range (1 g = 9.81 ms−2). The sensitivity of the device is demonstrated through the tracking of Earth tides and recording of ground motion corresponding to a number of teleseismic events over several months. These results demonstrate that vibrating beam MEMS accelerometers can be employed for measurements requiring high levels of stability and resolution with wider implications for precision measurement employing other resonant-output MEMS devices such as gyroscopes and magnetometers.
Similar content being viewed by others
Introduction
Recent advances in microelectromechanical systems (MEMS) have enabled the widespread development of sensors for a variety of consumer, automotive, and wearable healthcare electronics applications. Highly precise instruments, e.g., the atomic force microscope1 and ultra-stable clocks2 have also employed advances in MEMS technology for precision manufacturing of sensitive transducers and chip-scale system integration. MEMS technology combines miniaturization benefits (size, weight, and power) with a scalable manufacturing platform. Inertial sensors, in particular, have seen widespread application in the consumer and automotive electronics industries; there is increasing interest in developing highly precise accelerometers for seismic3 and gravity measurements4,5, as well as for navigation systems for semi-autonomous vehicles and pedestrians. Further applications for portable high-precision MEMS gravimeters and seismometers include monitoring of natural hazards, geotechnical surveying, and space missions. In this context, Lewis et al. recently demonstrated a remote surface gravity traverse on Mars using compact and robust instrumentation based on MEMS accelerometers integrated as part of the inertial measurement unit (IMU) on the Curiosity rover6; surveys on future planetary missions will require sensors with significantly higher accuracies, as well as the potential to combine background seismic measurements within the same module in alignment with device specifications reported in this paper.
Conventional MEMS accelerometers are typically based on a mass-spring system3,4,5, where design considerations concerning sensitivity and signal-to-noise run counter to dimensional scaling. A simple analysis based on Hooke’s law (see supplementary text) shows that the sensitivity of traditional accelerometers based on displacement-measurement scales inversely as the mass of the device or the inverse squared of the natural frequency4, which is counter to device robustness7 and miniaturization. Additionally, nonlinear springs4,5 are often employed in the engineering of such devices (in order to reduce the natural frequencies to a few Hz) introducing a significant additional calibration burden and an intrinsically limited measurement dynamic range. Furthermore, the potential to combine sensitive measurements over a wide dynamic range (> ±1 g) is a desirable feature in differential gravimeters in order to address inherent sensitivity to tilt and compensate for Earth’s background gravity field in terrestrial measurements.
Macroscopic accelerometers based on vibrating elements8,9 have previously been employed for applications demanding both accuracy and robustness. The early devices consist of a suspended mass connected to a vibrating wire under tension, such that the inertial force experienced by the mass due to gravity or an external acceleration is communicated as a variation in the axial tension of the wire, thereby modulating its natural frequency of vibration. The natural frequency of the vibrating element is continuously tracked through the implementation of a feedback oscillator circuit whose output frequency is proportional to the magnitude of the applied acceleration. Gilbert et al. proposed a vibrating wire gravimeter in 1949 for borehole measurements based on this principle9. Vibrating wire accelerometers were further developed for ship-borne10 and lunar gravimetry11.
More recently, vibrating beam resonant accelerometers have been miniaturised using silicon MEMS technology12,13,14 operating on similar principles. These MEMS accelerometers and other previous variants based on resonant sensing principles demonstrated significant drift from uncompensated environmental effects, particularly temperature variations, making them unsuitable for long-term, precision measurements. In this paper, we describe the development of the first MEMS vibrating beam accelerometer (VBA) that meets the stability requirements for use as a relative gravimeter and long-period seismometer. The sensing principle is based on monitoring resonant frequency shifts in vibrating beams, with drift compensated using a differential frequency readout configuration and active, chip- and module-level temperature control. The devices, which are fabricated in a silicon MEMS foundry using standard processes, demonstrate excellent stability over long integration times and are robust enough for field use. As opposed to mass-spring accelerometers, the scale factor of a vibrating beam gravimeter is length scale-invariant to first order (see Supplementary Information) and therefore, miniaturization does not have a detrimental impact on sensitivity or robustness.
Device fabrication and assembly
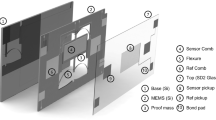
The mechanical element of the sensor consists of a spring-supported mass with a natural frequency of approximately 1 kHz (Fig. S2) micromachined from the silicon device layer of a silicon-on-insulator (SOI) wafer15 using a deep-reactive ion etch process16. The sensor mass is approximately 6.83 milli-grams and the spring constant for translational motion along the sensitive axis is approximately 260 N/m. This mass is mechanically linked to the vibrating beam elements through a lever mechanism14 such that the axial force on the beams is proportional to the inertial force on the mass amplified by a factor of approximately 25. The vibrating beams are driven by electrodes located on either side of the beam, as illustrated schematically in Fig. 1(a). These beams can be driven in either the fundamental or the second-order flexural mode of vibration (see Fig. S3) using electrostatic actuation; the higher-order mode enables a further increase in scale factor for a given topology. Two nominally identical beams are located on either side of the mass, to provide a differential push-pull output response. Integrated parallel-plate capacitive transducers enable recording of the motional response of the vibrating beams.
Fusion bonding of silicon wafers16 is employed to seal the device within a vacuum environment, with the device layer sandwiched within a three-wafer stack (Fig. S1) and sealed in a stable, low-pressure vacuum environment17. Through-silicon-via (TSV) electrical interconnects18 connect structures on the device wafer to external electronics and a top wafer is bonded to achieve vacuum encapsulation of the suspended proof mass and attached resonators. The wafer-level vacuum encapsulation provides a stable local environment for the devices and reduces the impact of fluid drag19 so that the quality factor Q of the vibrating beam is typically higher than 30,000 for both the fundamental and second order flexural modes. The Q of the beams is primarily limited by a combination of thermo-elastic damping20 and energy loss through the anchors.
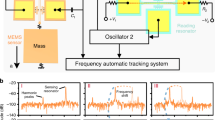
Following device fabrication, the wafer is diced and individual die are assembled onto custom chip carriers, as pictured in Fig. 1(b). The chip carrier consists of a heater element located underneath for temperature control. A copper mounting block is integrated on the top surface to provide shielding. The carrier is assembled onto a PCB stack and interfaced to custom front-end electronics, which consists of low-noise transimpedance amplifiers and a digital phase-locked loop to continuously track shifts in resonant frequency. Two output channels (one corresponding to each detector beam) are simultaneously recorded to provide continuous tracking of the resonant frequencies. A schematic of the device and associated front-end electronics is shown in Fig. 1(a). Temperature control of the sensitive external analogue front-end electronics is implemented within the sensor module (Fig. 1(c)) while local thermal control of the accelerometer chip21 enables active cancellation of the temperature-induced drift of the natural frequency. The drift arises due to the temperature sensitivity of the material properties of single-crystal silicon and can be reduced through additional active and passive compensation schemes22. A dedicated PC running National Instruments LabVIEW acquires the data generated from the module and consists of a custom frequency counter implemented to record the frequencies of the two channels to an accuracy of better than 1 μHz (Fig. S10). The data acquisition interface also allows simultaneous recording of temperature (at various locations within the sensor module, including the chip temperature), pressure, and power consumption of the temperature controllers to enable further corrections to be applied to the data through post-processing.
Results
The devices are initially characterised on a tilt platform14, in which the sensitive axis is oriented at specified tilt angles relative to the vertical to obtain an estimate of the scale factor and also to characterise the tilt sensitivity of the device. The tilt sensitivity arises due to the large background gravitational field and varies as the cosine of the angle between the sensitive axis of the device and true local vertical as defined by the direction of the background field23. Next the output from the device is recorded with the sensitive axis aligned to the horizontal position without the external temperature control operating. The noise spectrum for this measurement is provided in Fig. S10 demonstrating a noise floor of 25 nano-g/√Hz at 1.5 Hz. Finally, the device is oriented with the sensitive axis aligned to the vertical4 with the external temperature control now operational to obtain data demonstrating sensitivity to tidal effects. The testing was conducted in a Cambridge University lab with significant background seismic noise, a lower noise basement laboratory at the University of Bristol, as well as at a low-noise observatory in Eskdalemuir, Scotland.
The experimentally measured sensor scale factor for the selected device is 5972 Hz/g when the beams are operated in the second mode, close to the simulated value (Fig. S4). Figure 2(a) plots the acceleration noise power spectral density (PSD) of the device measured at Eskdalemuir, while Fig. 2(b) plots this for measurements from the Cambridge University lab with 5 independent datasets in each location overlaid on the same plot to demonstrating the repeatability of the measurements at different times under ambient test conditions. The noise floor of the fully integrated module is seen to be below 100 μGal/√Hz when the device is mounted vertically and measured in a low-noise seismic vault, with a higher noise floor recorded in the noisier University lab environment, due to the ambient seismic background. When operated continuously, a burn-in period of approximately two weeks was required prior to the device response exhibiting a continuous linear drift of approximately ~4 mHz/hour. This drift is cancelled in software by fitting to the linear trend and recovering the residual variations. The linear drift is thought to arise due to a variety of aging effects, not intrinsic to the device but due to package-induced stress, which has been shown to impact the drift characteristics for MEMS resonators24. Once the linear drift is cancelled, which is standard practice for relative gravimeters4,5, it is seen that the response is extremely stable, enabling gravity and seismic measurements over long time scales (100 s – 200000 s). Figure 2(c,d) plot the Allan Deviation25 of the output response over a 10000 s period for the same datasets (the Allan Deviation of the response prior to drift correction is plotted in Fig. S6), showing that the high frequency noise is averaged out over a period of 1000 s representative of the recording period for a single surface gravity measurement. An output Allan deviation of 9 μGal at 1000 s is recorded for one of the Cambridge University lab datasets. A similar stability is recorded when the device is run in a seismic vault operated by the British Geological Survey (Fig. 2(d)) with the micro-seismic background26 having prominent peaks in the frequency range 0.1 Hz – 0.5 Hz, which are also seen in the acceleration noise power spectrum plots. The device was then left running for a period of several days at the University lab and about 36 hours at the seismic vault for longer duration measurements. The output response from these measurements demonstrates tracking of the variations in the gravitational field due to Earth tides. Figure 3 plots the Allan deviation of the response measured in the seismic vault over the 36 hour period with the drift-compensated data averaged over a period of 12800 s, similar to the timescale reported in4. This is compared to the data obtained from the software TSoft27 and a statistical correlation R of 0.86 is noted for this dataset. Longer duration measurements were possible in the University lab where a statistical correlation R of 0.92 is noted between the conditioned MEMS dataset (see Methods section) and the predicted Earth tides model from TSoft following correction for ocean loading effects over a period of 4 days as shown in Fig. 4. Longer timescale measurements over the course of 6 days demonstrated a lower statistical correlation R of 0.88 due to the residual nonlinearity in the drift over this duration. The device also recorded the ground motion from a number of teleseismic events during the recording period, prominent among them being the Chiapas, Mexico earthquake on September 7, 2017 at the University of Bristol basement laboratory, demonstrating excellent performance as a long-period seismometer. Spectrograms corresponding to the recorded response of the MEMS sensor for this Mw8.2 event are compared to that from a reference seismometer (Guralp CMG3TD broadband seismometer located in Swindon, UK in the existing British Geological Survey monitoring network) in Fig. 5, with good agreement demonstrated. Deviations at low frequencies (<0.01 Hz) are attributed to the roll-off in the frequency response of the reference seismometer at these frequencies and the slow tilt of the platform in Bristol on which the sensor was mounted. A further example of recorded ground motion for the Oaxaca, Mexico earthquake on February 16, 2018 is shown in Figs. S8,S9.
Accelerometer noise power spectral density measurement (five independent repeat measurements overlaid) for responses recorded (a) in a seismic vault at Eskdalemuir, Scotland demonstrating a noise floor of <100 μGal/rt-Hz, and (b) in the Cambridge University lab. The corresponding Allan deviation data has been plotted in (c),d) demonstrating a bias stability of <10 μGal for an integration time >1000 s following linear drift correction.
Allan deviation data showing tracking of Earth tides in the seismic vault at Eskdalemuir, Scotland. The statistical correlation coefficient R between the measured time series and the predicted Earth tide model (TSoft)27 is 0.862 over this period for this dataset. The blue solid lines show the Allan deviation for the MEMS sensor with the dashed orange lines plotting the Allan deviation for the theoretical data generated by TSoft.
Data showing tracking of Earth tides over a four day period at the University laboratory. The solid line indicates the conditioned MEMS dataset and the dashed line indicates the theoretical prediction from TSoft with an ocean loading correction applied. The statistical correlation coefficient R between the measured time series and the predicted Earth tide model (TSoft)27 is 0.92 over this period.
Spectrograms of the measured ground acceleration for (a) the MEMS sensor module located in a basement laboratory in Bristol, UK, and (b) a reference seismometer located in Swindon, UK, for the 2017 Chiapas, Mexico, Earthquake (Mw 8.2) on September 8 2017. The MEMS accelerometer output was sampled at 1 Hz while the reference accelerometer was sampled at 50 Hz.
Summary and Future Outlook
Highly accurate and compact MEMS accelerometers are of great interest for a variety of applications. These devices can be integrated into small-diameter wireline tools and other borehole instruments for tracking fluids in the sub-surface28 with application to flood front monitoring29, carbon sequestration30, and mining. Surface gravity measurements are widely used for a variety of applications in exploration31, geotechnical surveying, identification of sub-surface voids caused by tunnelling or natural sinkholes32, monitoring magma flow in volcanic zones33, and inertial navigation. The availability of a compact, potentially low-cost and portable device significantly expands the application spectrum of gravimetry, which are limited by the expensive and fragile sensors. By reducing the cost associated with the manufacturing these monitoring instruments, arrays of tens of thousands of sensors can be deployed and wirelessly networked to address applications such as routine geotechnical surveying, monitoring fluid movement in the sub-surface (e.g., for management of underwater aquifers or CO2 storage monitoring), monitoring ground movement (slope stability) or as sensitive tilt meters for construction applications. Their response to seismic and micro-seismic events enables these devices to be deployed in large-scale monitoring networks, replacing more expensive and fragile instruments currently employed for these purposes. These results also have implications for the development of other resonant devices, such as navigation-grade MEMS gyroscopes, which require excellent bias stabilities over long integration times.
The MEMS VBA reported in this work provides several advantages over existing macroscopic instruments and consumer-grade MEMS accelerometers, including the ability to measure over a wide dynamic range ±1 g while enabling sufficient resolution for gravity measurements in the regime below 10 μGal. Furthermore, the devices are inherently robust to shock and vibration with a fundamental natural frequency of ~1 kHz, as opposed to displacement output devices based on optical or capacitive sensing that must be designed around a low operating natural frequency of <10 Hz to address measurements of similar resolution. Additionally, the resonant sensing principle scales favourably with the scaling of dimensions with, millimetre-scale devices currently in production meeting performance specifications exceeding those outlined in this first-generation device. Miniaturisation of the MEMS VBA and further integration including implementation of the associated electronics on a CMOS chip could result in portable gravimeters dissipating power <100 mW, representing a significant step change improvement in both metrics relative to current technology. The associated reduction in cost could enable a range of applications that are inaccessible for current highly sensitive, precise accelerometers.
Methods
Microfabrication
The fabrication process for the MEMS sensors commences with the manufacture of a VIA wafer incorporating through-silicon vias17 and a shallow etch to provide vertical clearance for the released MEMS devices. This wafer is then bonded16 to a second SOI wafer which is thinned down with the substrate layer sacrificed while leaving the device layer intact. Deep reactive ion etching16 is used to etch through the silicon device layer to create the device features, including the proof mass, suspension systems, vibrating beam elements and electrodes. Finally, a third silicon wafer is etched to create a cavity to house the mechanical devices and the final wafer stack (Supplementary Fig. S1) is created through wafer bonding under vacuum in an external silicon MEMS foundry.
Electrical interface
The resonant beams are driven in closed-loop oscillation using a custom designed analogue front-end interface comprising a low-noise trans-impedance amplifier (TIA) front-end and a digital phase-locked loop (Zurich Instruments MFLI) in order to separately track the resonant frequencies of each of the two beams. The output signals are then digitized and the data is captured on a PC (National Instruments Data Acquisition platform) where a frequency counter is implemented for each channel using a DFT-based technique. A differential frequency output is calculated by subtracting the frequencies of each of the two oscillators to provide a first-order cancellation of environmental effects (see Supplementary Fig. S11).
Environmental control and shielding
Three stages of temperature control are employed. The first stage regulates the chip temperature to a value of ±250 µ°K of a given set-point (50 °C for measurements reported in this work). The second stage controls the temperature of the surrounding analogue electronics to ±1 mK of a set-point (45 °C for measurements reported in this work) and a third stage allows for control of the temperature of entire module to a similar precision. The chip and the entire front-end electronics assembly are housed in a shielded box to prevent external electromagnetic interference.
Earth tide data processing
The linear drift was removed from the raw data using a sliding window of duration 86400 s. A Savitzky-Golay FIR smoothing filter with polynomial order of 3 and frame length 7200 s was further applied to the linear drift corrected data. Finally, a moving mean with length 60 s was used to smooth the curve.
Data availability
The time-series data underpinning the findings of this study are available in the University of Cambridge data repository with the identifier https://doi.org/10.17863/CAM.39454.
References
Binning, G., Quate, C. F. & Gerber, C. Atomic Force Microscope. Phys. Rev. Lett. 56, 930 (1986).
Knappe, S. et al. A microfabricated atomic clock. Appl. Phys. Lett. 85, 1460 (2004).
Pike, W. T., Standley, I. M., Calcutt, S. B. & Mukherjee, A. G. A broad-band silicon microseismometer with 0.25 ng/rt-Hz performance. Proc. IEEE MEMS 2018, 113–116 (2018).
Middlemiss, R. P. et al. Measurement of earth tides with a MEMS gravimeter. Nature 531, 614–617 (2016).
Tang, S. et al. A high-sensitivity MEMS gravimeter with a large dynamic range. Microsyst. Nanoeng 5, 45 (2019).
Lewis, K. et al. A surface gravity traverse on Mars indicates low bedrock density at Gale crater. Science 363, 535–537 (2019).
Boser, B. E. & Howe, R. T. Surface-micromachined accelerometers. IEEE J. Solid-State Circuits 31(3), 366–375 (1996).
Gilbert, R. L. G. A dynamic gravimeter of novel design. Proc. Phys. Soc., B 62, 445–454 (1949).
Gilbert, R. L. G. Gravity observations in a borehole. Nature 170, 424–425 (1952).
Wing, C. G. MIT vibrating string surface-ship gravimeter, J. Geophys. Res., 5882-5894, (1969).
Henderson, G. C. & Iverson, R. M. Testing gravimeters for lunar surface measurements. IEEE Trans. Geosci. Electron., GE- 6(3), 132–138 (1968).
Seshia, A. A. et al. A vacuum packaged surface micromachined resonant accelerometer. J. Microelectromech. Syst. 11(6), 784–793 (2002).
Zou, X., Thiruvenkatanathan, P. & Seshia, A. A. A seismic-grade resonant MEMS accelerometer. J. Microelectromech. Syst. 23(4), 768–770 (2014).
Pandit, M. et al. An ultra-high resolution resonant MEMS accelerometer, Proc. 2019 IEEE MEMS, Seoul, Korea, pp. 664-667 (2019).
Amini, B. V. & Ayazi, F. Micro-gravity capacitive silicon-on-insulator accelerometers. J. Micromech. Microeng. 15, 2113–2120 (2005).
Klassen, E. H. et al. Silicon fusion bonding and deep reactive ion etching: a new technology for microstructures. Sens. Act. A 52, 132–139 (1996).
Rimskog, M. Through Wafer Via Technology for MEMS and 3D Integration, 2007 32nd IEEE/CPMT International Electronic Manufacturing Technology Symposium, 286-289 (2007).
Esashi, M. Wafer level packaging of MEMS. J. Micromech. Microeng. 18, 073001 (2008).
Ikeda, K. et al. Three-dimensional micromachining of silicon pressure sensor integrating resonant strain gauge on diaphragm, Sens. Actuators A: Phys 23, 1007–1010 (1990).
Lifshitz, R. & Roukes, M. Thermoelastic damping in micro and nanomechanical systems. Phys Rev B 61(8), 5600–5609 (2000).
Mustafazade A. & Seshia A. A. Compact High-Precision Analog Temperature Controller for MEMS Inertial Sensors, Proc. 2018 IEEE Intl. Freq. Control Symposium, 2018.
Van Beek, J. T. M. & Puers, R. A review of MEMS oscillators for frequency reference and timing applications. J. of Micromech. Microeng. 22, 013001 (2012).
Niebauer, T. M., Blitz, T. & Constantino, A. Off-level corrections for gravity meters. Metrologia 53, 835–839 (2016).
Tatar, E., Mukherjee, T. & Fedder, G. K. Stress effects and compensation of bias drift in a MEMS vibratory rate gyroscope. J. Microelectromech. Syst. 26(3), 569–579 (2017).
Malkin, Z. Application of the Allan Variance to time series analysis in astrometry and geodesy. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control 63(4), 582–589 (2016).
Peterson, J. Observations and modeling of background seismic noise, U.S. Geol. Surv. Open-File Rept. 93–322 (1993).
Van Camp, M. & Vauterin, P. Tsoft: graphical and interactive software for the analysis of time series and Earth tides. Comput. Geosci. 31, 631–640 (2005).
Schultz, A. K. Monitoring fluid movement with the borehole gravity meter. Geophysics 54(10), 1267–1273 (1989).
Hare, J. L., Ferguson, J. F., Aiken, C. L. V. & Brady, J. L. The 4D microgravity method for waterflood surveillance: A model study for the Prudhoe Bay reservoir, Alaska. Geophysics 64(1), 78–87 (1999).
Sherlock, D. et al. Gravity monitoring of CO2 storage in a depleted gas field: a sensitivity study. Explor. Geophys. 37, 37–43 (2006).
Nabighian, M. N. et al. Historical development of the gravity method in exploration, Geophysics 70(6), 63ND–89ND (2005).
Butler, D. K. Microgravimetric and gravity gradient techniques for detection of subsurface cavities. Geophysics 49(7), 1084–1096 (1984).
Battaglia, M., Gottsmann, J., Carbone, D. & Fernandez, J. 4-D volcano gravimetry, Geophysics 73(6), WA3–WA18 (2008).
Acknowledgements
The authors would like to acknowledge the British Geological Survey and the University of Bristol Nanoscience and Quantum Information Laboratory for access to low-noise test facilities. Funding for this project was provided by a grant from Innovate UK and the Natural Environment Research Council (NERC) under grant number NE/N012097/1.
Author information
Authors and Affiliations
Contributions
A.A.S. conceived the VBA implementation, with input from R.T.H.; X.Z. and A.A.S. designed the devices and the fabrication process; X.Z. performed the finite element simulations for the designs; C.Z., A.M. and A.A.S. designed the front-end electronics, A.M. designed and implemented the sensor module, temperature controllers, data acquisition interface, and precision feedback circuits; A.M., C.Z., G.S., M.P., P.S., A.A.S. contributed to the testing and experimental characterisation of the devices; A.M., M.P., Z.D., C.Z., G.S., A.A.S. contributed to the data processing and data analysis; A.A.S., A.M. and M.P. wrote the manuscript with inputs from all other authors; all authors commented on the results and contributed to the editing of the manuscript; A.A.S. supervised the research.
Corresponding author
Ethics declarations
Competing interests
A.M., M.P., G.S., Z.D. and P.S. are employees of Silicon Microgravity. R.T.H. is a Board Advisor of Silicon Microgravity. A.A.S. is a co-founder and Director of Silicon Microgravity.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mustafazade, A., Pandit, M., Zhao, C. et al. A vibrating beam MEMS accelerometer for gravity and seismic measurements. Sci Rep 10, 10415 (2020). https://doi.org/10.1038/s41598-020-67046-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-020-67046-x
This article is cited by
-
A self-centering and stiffness-controlled MEMS accelerometer
Microsystems & Nanoengineering (2024)
-
Modeling, Simulation, and Optimization of Piezoelectrically Actuated Dual-Axis MEMS Accelerometer for Seismic Sensing
Journal of Vibration Engineering & Technologies (2023)
-
Triple sensing scheme based on nonlinear coupled micromachined resonators
Nonlinear Dynamics (2023)
-
Electrostatic nonlinear dispersive parametric mode interaction
Nonlinear Dynamics (2023)
-
Nonlinear dynamics of a tunable novel accelerometer, tunable with a microtriple electrode variable capacitor
Acta Mechanica (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.