Vortex phases and glassy dynamics in the highly anisotropic superconductor HgBa₂CuO_4+δ

Abstract

We present an extensive study of vortex dynamics in a high-quality single crystal of HgBa₂CuO_4+δ, a highly anisotropic superconductor that is a model system for studying the effects of anisotropy. From magnetization M measurements over a wide range of temperatures T and fields H, we construct a detailed vortex phase diagram. We find that the temperature-dependent vortex penetration field H_p(T), second magnetization peak H_smp(T), and irreversibility field H_irr(T) all decay exponentially at low temperatures and exhibit an abrupt change in behavior at high temperatures T/T_c >~ 0.5. By measuring the rates of thermally activated vortex motion (creep) S(T, H) = |dlnM(T, H)/dlnt|, we reveal glassy behavior involving collective creep of bundles of 2D pancake vortices as well as temperature- and time-tuned crossovers from elastic (collective) dynamics to plastic flow. Based on the creep results, we show that the second magnetization peak coincides with the elastic-to-plastic crossover at low T, yet the mechanism changes at higher temperatures.

Introduction

Interest in copper-oxide superconductors (cuprates) is fueled by their technological potential and the outstanding mystery of the mechanism governing high-temperature superconductivity, which stifles prediction of new superconductors. It is known that, in cuprates, superconductivity is hosted in the crystallographic ab-planes. This induces anisotropy γ between the in-plane (ab) and out-of-plane (c-axis) fundamental superconducting parameters, such as the penetration depth λ_ab = λ_c/γ and coherence length ξ_ab = γξ_c. When evaluating the potential of superconductors for technological applications, high anisotropy compels considerations beyond the typical metrics of high critical temperature T_c, critical current density J_c, and upper critical field H_c2. This is because thermal fluctuations profoundly impact anisotropic materials’ electronic and magnetic properties, which are significantly influenced by the dynamics of vortices. Consequently, thermally activated vortex motion (creep) is fast and J_c vanishes at an irreversibility field H_irr that can be much less than H_c2, potentially negating the otherwise advantageous properties of these materials. Understanding vortex dynamics in cuprates is not only technologically relevant, but also can substantially contribute to the debate over the degree to which superconductivity in cuprates is conventional¹.

Magnetic flux penetrates superconductors immersed in fields greater than the lower critical field H_c1. This does not quench superconductivity in high-T_c materials provided that the field remains below H_c2. In layered cuprates, interior flux can appear as stacks of weakly-coupled 2D pancake vortices, each localized on a Cu-O plane. Pancake vortices within a stack are not necessarily aligned and interact both magnetically (owing to their moments) and through Josephson coupling between pancakes in adjacent planes. If this coupling is sufficiently strong, the stacks may behave as continuous strings, hence be considered 3D vortex lines. The differing dynamics of 2D pancakes and 3D vortex lines should therefore play a major role in determining the phase diagram in highly anisotropic materials.

The superconductor HgBa₂CuO_4+δ (Hg1201) is recognized as ideal for systematically studying the effects of high anisotropy. This is because its clean microstructure enables probing intrinsic, rather than sample-dependent, properties associated with high anisotropy². Specifically, Hg1201 crystals do not contain common defects, such as twin-boundaries and rare-earth-oxide precipitates^3,4,5. Furthermore, it has a simple tetragonal structure and optimally doped Hg1201 has the highest T_c among single Cu-O layer materials, permitting thorough studies of the effects of thermal fluctuations on the superconducting state. Despite these desirable characteristics, the paucity of research on Hg1201 results from the challenges of growing large, high-quality single crystals.

In this paper, we identify vortex phase boundaries and glassy regimes in the vortex phase diagram of a clean, optimally doped Hg1201 single crystal. We find that the temperature-dependent vortex penetration field H_p(T), second magnetization peak H_smp(T), and irreversibility field H_irr(T) all decay exponentially at low temperatures and exhibit an abrupt change in behavior at high temperatures. We present complementary vortex creep measurements over a wide range of the phase diagram that reveal the broad extent to which the dynamics of pancake vortices determine the magnetic properties in our sample. Our main findings from these measurements are as follows: First, the crystal hosts a vortex glass state characterized by collective creep of large bundles of pancake vortices at low temperatures T/T_c ≤ 0.4 and applied fields μ₀H < 0.5 T. The glass state persists at higher fields, yet the bundle size shrinks. Second, we find temperature-tuned crossovers from elastic (collective) dynamics to plastic flow. By measuring at the crossover temperature over an extended time frame, we additionally capture a transition from elastic to plastic dynamics over time. Last, we show that the second magnetization peak does not originate from elastic-to-plastic crossovers over most of the phase diagram; these crossovers only coincide with the second magnetization peak at low temperatures T/T_c < 0.2.

Results

Critical temperature and anisotropy

Two of the sample’s key characteristics, the critical temperature T_c and the anisotropy γ, were extracted from temperature- and field-dependent magnetization measurements as summarized in Fig. 1. The temperature sweeps M(T) in a field of 5 Oe yielded a critical temperature of T_c ≈ 95.9 K, see Fig. 1(a), consistent with near optimal doping^2,6. To determine the anisotropy, we measured the ratio of the transverse (M_T) to the longitudinal (M_L) magnetization at various field orientations (θ) relative to the c axis in the reversible (vortex liquid) regime. The raw data is plotted in Fig. 1(b,c). As shown in Fig. 1(d), a least squares fit of the data to Eq. (1), the Kogan model^7,8,

$$\frac{{M}_{T}}{{M}_{L}}=(1-{\gamma }^{2})\frac{\sin \,\theta \,\cos \,\theta }{{\sin }^{2}\theta +{\gamma }^{2}{\cos }^{2}\theta },$$

(1)

Figure 1

(a) Temperature dependent magnetization M(T) measured at H = 5 Oe after zero-field cooling, revealing T_c ≈ 95.9 K, consistent with expectations for optimally doped Hg1201. Angular dependence of the (b) transverse (M_T) and (c) longitudinal (M_L) components of the magnetization, and (d) the ratio M_T/M_L in an applied field of 0.1 T and temperatures 80 K and 85 K. Note that in (d), the data for the two temperatures overlap and the black curve is a fit of the 80 K data to Eq. (1) that yields an anisotropy factor γ ≈ 32.

produces an anisotropy of γ ≈ 32. This is consistent with previous work on optimally doped Hg1201 single crystals. Specifically, angle dependent torque magnetometry studies^9,10,11,12 found γ ≈ 27−30. Additionally, a study¹³ that measured the magnetization at two field orientations, perpendicular (M_⊥) and parallel (M_||) to the CuO₂ planes, found γ ≈ 30 using a self-consistency equation from anisotropic Ginzburg-Landau theory M_⊥(H) = γM_||(γH).

Irreversible Magnetization

Isothermal magnetization loops were recorded for H||c and at T = 5−65 K. Select curves are displayed in Fig. 2. In all cases, the field was first swept to −3 or −4 T (not shown) to establish the critical state (full flux penetration throughout the sample). The lower branch of the loop was subsequently measured as the field was ramped from 0 T to 7 T, and the upper branch was collected as the field was swept back down. All curves exhibit a distinct shape with two conspicuous features: a dip in the magnitude of M near the onset field H_on and a second magnetization peak (SMP) at H_smp. In general, this shape and the magnitude of the magnetization is indicative of a weak vortex pinning regime at low fields ($H\lesssim {H}_{on}$) and stronger pinning at higher fields. We observed similar results in measurements of our other Hg1201 crystals. The source of pinning is likely point defects in the Hg-O layer—specifically, oxygen interstitials and mercury vacancies^3,4,5, and this should be the main source of disorder in the bulk that hinders thermal wandering of vortices.

Figure 2

Isothermal magnetic hysteresis loops M(H) at multiple temperatures for a HgBa₂CuO_4+δ single crystal. Each curve exhibits a low field dip at H_on and a second magnetization peak at H_smp.

In high-temperature superconducting crystals, a surface barrier—called the Bean-Livingston (BL) barrier—often plays a significant role in determining the magnetic properties and shaping the M(H) loops^14,15,16,17. It originates from competing effects: vortices are repelled from the surface by Meissner shielding currents and attracted by a force arising from the boundary conditions (usually modeled as the attraction between the vortex and an image antivortex¹⁸). Disappearing at the penetration field H_p ≈ κH_c1/lnκ, the BL barrier impedes vortex entry and exit from the sample in fields less than H_p > H_c1, where H_c1 is the lowest field at which flux penetration is thermodynamically favorable. The contribution of the barrier is magnified in materials with high Ginzburg-Landau parameters κ = λ/ξ and diminished by surface imperfections. Creep of pancake vortices over the barrier produces the exponential temperature dependence¹⁷

$${H}_{p}(T)\simeq {H}_{c}{e}^{-T/{T}_{0}},$$

(2)

where T₀ = ε₀dln(t/t₀), ${\varepsilon }_{0}={\Phi }_{0}^{2}/4\pi {\mu }_{0}{\lambda }_{ab}^{2}$ is the vortex line energy or tension, d is the spacing between CuO₂ planes, t is the time scale of the measurement, t₀ ~ 10⁻¹⁰–10⁻⁸ s relates to the vortex penetration time¹⁹, and the thermodynamic critical field is ${H}_{c}={\Phi }_{0}/2\sqrt{2}\pi {\xi }_{ab}{\lambda }_{ab}$.

To investigate the relevance of surface barriers in our sample, we measured the field at which vortices first penetrate into the sample peripheries H_p by collecting the zero-field cooled M(H) isotherms shown in Fig. 3(a): we defined H_p as the field at the departure from linearity. Figure 3(a) inset shows the extraction technique and the phase diagram in Fig. 4 contains the resulting temperature dependence. We find that H_p(T) follows Eq. (2) at low temperatures T/T_c < 0.55, and a least squares fit produces T₀ = 21.3 ± 0.7 K and H_c = 0.06 T. The experimentally extracted T₀ is reasonably close to the estimate T₀ = 26 K, calculated assuming t ~ 100 s, t₀ = 10⁻¹⁰ s, d ≈ 9.5 Ź³, and λ_ab ≈ 162 nm²⁰.

Figure 3

(a) M versus H at low fields after zero field cooling. H_p is the field at which each curve deviates from a linear fit to the Meissner slope (black line). Inset shows the deviation ΔM from the Meissner slope and the black horizontal line indicates the criterion used for defining H_p (a deviation of a tenth of the standard deviation σ ≈ 0.003 from the linear fit). (b) Magnification of magnetization loops plotted in Fig. 2 (collected after full flux penetration) showing a weak pinning regime at low fields in which M is low and weakly sensitive to magnetic field. (c) Temperature dependence of the magnetization showing transition from the irreversible regime to the reversible regime to the normal state. The upper (lower) branches were collected after the critical state was prepared by sweeping the field to >Δ4H^* above (below) the indicated fields. The irreversibility point (T_irr, H_irr) is defined as the point at which the upper and lower branches merge.

Figure 4

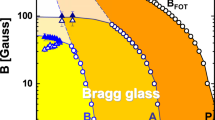
Vortex phase diagram for our Hg1201 crystal, determined by behavior extracted from fits to data shown in Fig. 3. The solid blue line is a fit to Eq. (2), while the dashed blue line is a fit to ${H}_{c1}(T)=[{\Phi }_{0}/(4\pi {\lambda }_{ab}^{2}(T)$$(1-N))]\,\mathrm{ln}\,\kappa$. The solid red line is a fit of the low temperature second magnetization peak data to ~e^−AT for constant A. Lastly, the solid purple line is a fit to ${e}^{-T/{T}_{0}}$ and the dashed purple curve is a fit to (1−T/T_c)^m.

To accurately assess the field of first penetration, we must account for local field enhancements due to demagnetizing effects by multiplying our extracted value by 1/(1 − N), where N is the effective demagnetizing factor. Expressing the field enhancement in terms of a demagnetizing factor formally exclusively applies to samples with elliptic cross-section (per refs. ^21,22). For samples with rectangular cross-section (width w and thickness δ, $w\gg \delta$), we must account for the fact that the field of first penetration is retarded by a geometrical barrier^23,24. This barrier is associated with a parametrically lower field enhancement at the sample edge as compared to an elliptic slab with the same dimensions. In this case, accurate values of the effective demagnetizing factors for rectangular prisms have been calculated numerically²⁵. Following the calculations from ref. ²⁶, we find N ≈ 0.75 which yields H_c = 0.24T and hence a coherence length ξ_ab(0) ~ 1.5 nm, similar to the value of ξ_ab(0) ~ 2.0 ± 0.4 nm measured by Hofer et al.¹¹. We attribute the deviation of the penetration field at low temperature from the expected scaling of H_c1(T), see Fig. 4 for T/T_c < 0.55, to the increasing importance of thermal creep to overcome the surface/geometric barriers.

Agreement of our H_p(T < 0.55T_c) data with Eq. (2) indicates that, at low T, vortices enter as pancakes (as evinced by creep measurements, see discussion in the next section) and are thermally activated over the BL barrier. At T/T_c ~ 0.55, the temperature dependence of H_p abruptly changes, suggestive of a different mechanism for vortex penetration at higher temperatures. Similar crossovers have been observed in other layered superconductors^{16,27,28,29,30,31} around T/T_c ~ 0.5. We anticipate such a crossover when H_p(T) from Eq. (2) falls below H_c1: in this case, we would expect H_p(T) to be bound by $(1-N){H}_{c1}(T)=[{\Phi }_{0}/(4\pi {\lambda }_{ab}^{2}(T))]\,\mathrm{ln}\,\kappa$ for T above the crossover. Considering the two-fluid approximation, λ_ab(T) = λ_ab(0)[1−(T/T_c)⁴]^−1/2, and a T-independent κ, this expression indeed fits the data for H_c1 = 300Oe, see Fig. 4. A competing scenario for the crossover—based on a transition of creep of pancakes to creep of vortex half-loops^17,31—fails to produce the correct temperature dependence for T/T_c > 0.55. From this value for H_c1 we extract λ_ab(0) = 154 nm, which is comparable with published data^11,20.

For fields above H_p, but below H_smp, |M| dips to an ill-defined minimum and increases again at H_on. Figure 3(b) magnifies this low-field plateau and H_on(T) is plotted in Fig. 4. Previous studies have related H_on to a transition between an ordered vortex lattice at low fields and an entangled lattice created by point disorder at higher fields, tuned by competition between thermal, pinning, and elastic energies. For example, FeSe_1−x Te_x single crystals showed evidence of a Bragg glass (quasi-ordered vortex solid) below H_on³² and a presumed disordered vortex solid above H_on. Additionally, YBa₂Cu₃O_7−δ, Nd_1.85Ce_0.15CuO_4−δ, and Bi₂Sr₂CaCu₂O_8+δ all demonstrate disorder induced phase transitions that show a signature in the M(H) loops³³.

In applied magnetic fields above H_on, the magnetization apexes at the second magnetization peak H_smp. Second magnetization peaks have been reported in studies of most classes of superconductors, including low-T_c^34,35, iron-based^{32,36,37,38,39,40}, and highly anisotropic^28,41 materials, as well as YBa₂Cu₃O_7−δ (YBCO) single crystals⁴². In fact, this peak has also been observed in a few previous studies^{20,43,44,45,46} of Hg1201 single crystals grown by two research groups^4,45, though the peak is far more pronounced in our samples. This feature is typically either attributed to a crossover between vortex pinning regimes or a structural phase transition^47,48 in the vortex lattice. Below, we will revisit the discussion of the second magnetization peak because creep measurements are requisite to evaluate possible origins of the SMP.

At sufficiently high fields, the loops close as the system transitions into the reversible regime at the irreversibility field H_irr. Instead of extracting H_irr from the isothermal magnetization loops M(H), we extract it from isomagnetic M(T) sweeps. This is more precise than measurements involving sweeping the field: temperature sweeps tend to induce less noise than field sweeps and, at the transition, the upper and lower branches of M(T) not only converge, but also exhibit a sharp change in slope. Figure 3(c) contains select M(T) datasets showing the extraction technique and the resulting irreversibility line is shown in Fig. 4.

For T/T_c < 0.6, we find that H_irr(T) ∝ ${e}^{-T/{T}_{0}}$ (shown in Fig. 4), which yields T₀ = 19.7 ± 0.6 K, produced by a least squares fit. Notice that T₀ is close to the value T₀ ≈ 21 K, extracted in the fit of our H_p data to Eq. (2) and identical to the value (T₀ = 19.7 ± 0.4 K) extracted in another study on Hg1201 single crystals⁴⁵. At higher temperatures T > T^*, the shape of the irreversibility line changes. Similar trends in H_irr(T) have been found in grain-aligned Hg1201 samples⁴⁹ and single crystals⁴⁵.

Although the field of first penetration seems to be dominated by surface barrier effects, we conclude from the symmetric magnetization loops that bulk pinning is the dominant pinning source in our Hg1201 crystal after field penetration. Otherwise, i.e. if the contribution of bulk pinning were relatively insignificant, we would observe asymmetry between the upper and lower branches of the magnetization loops ¹⁸. Despite the observation of bulk pinning dominance, it remains unclear whether the similar exponential temperature scaling of H_p and H_irr have a common ground. Compiling the aforementioned results, Fig. 4 shows the resulting phase diagram on a semilog plot. In the following sections, we use magnetic relaxation measurements to learn more about the nature of vortex dynamics in the gray region of Fig. 4. The following sections present our main result – a more detailed understanding of vortex behavior derived from extensive vortex creep measurements.

Vortex creep

The disorder landscape defines potential energy wells in which vortices will preferentially localize to reduce their core energies by a pinning energy U₀. An applied or induced current tilts this energy landscape. This reduces the energy barrier that a pinned vortex must surmount to escape from a well to a current-dependent value U(J). The time required for thermal activation over such a barrier can be approximated by the Arrhenius form

$$t={t}_{0}{e}^{U(J)/{k}_{B}T}.$$

(3)

At low temperatures ($T\ll {T}_{c}$) and fields, the simple linear relationship U(J) = U₀(1 − J/J_c0) proposed in the Anderson-Kim model^50,51 is often accurate. However, because this model neglects vortex elasticity and vortex-vortex interactions, its relevance is often further limited to the early stages of the relaxation process ($J\lesssim {J}_{c0}$). In the later stages $J/{J}_{c0}\ll 1$, collective creep theories, which consider vortex elasticity, predict an inverse power law form for the energy barrier U(J) = U₀[(J_c0/J)^μ]. Here, the glassy exponent μ is sensitive to the size of the vortex bundle that hops during the creep process and its dimensionality. To capture behavior for a broad range of J, we invoke a commonly used interpolation between the two regimes

$$U(J)={U}_{0}[{({J}_{c0}/J)}^{\mu }-1]/\mu ,$$

(4)

where μ = −1 recovers the Anderson-Kim result. It is now straightforward to combine Eqs. (3) and (4) to determine the expected decay in the persistent current over time J(t) and subsequently the vortex creep rate S:

$$J(t)={J}_{c0}{\left[1+\frac{\mu {k}_{B}T}{{U}_{0}}\mathrm{ln}(t/{t}_{0})\right]}^{-1/\mu }$$

(5)

and

$$S\equiv |\frac{d\,\mathrm{ln}\,J}{d\,\mathrm{ln}\,t}|=\frac{{k}_{B}T}{{U}_{0}+\mu {k}_{B}T\,\mathrm{ln}(t/{t}_{0})}.$$

(6)

Creep measurements are a useful tool for determining the size of the energy barrier and its dependence on current, field, and temperature. Such measurements further probe the vortex state, revealing the existence of glassy behavior, collective creep regimes, or plastic flow. This is because, as evident in Eq. (6), creep provides access to both U₀ and μ. Table 1 summarizes expected values of μ for collective creep of 3D flux lines and 2D pancake vortices.

Table 1 Exponents μ predicted by collective creep theory^51,59.

To shed light on the Hg1201 phase diagram, we measured creep rates in a wide range of temperatures (5–60 K) and magnetic fields (0.1–5 T) using standard methods¹⁹, summarized here. We first establish the critical state by sweeping the field 4H^* above the field at which creep will be measured H, where H^* is the minimum field at which magnetic flux will fully penetrate the sample. Second, the field is swept to H, such that the magnetization M(H) coincides with its value on the upper branch of a magnetization loop. [If the magnitude of the initial field sweep were not sufficiently high, M(H) would instead fall inside the loop, vortices would not fully penetrate the entire sample and the previously discussed models would be inapplicable.] Third, the magnetization M(t) ∝ J(t) is subsequently recorded every ~15 s for an hour. We also briefly measure M(t) in the lower branch to determine the background arising from the sample holder, subtract this, and adjust the time to account for the difference between the initial application of the field and the first measurement (maximize correlation coefficient). Lastly, the normalized creep rate S(T, H) is extracted from the slope of a linear fit to lnM−lnt.

Figure 5 shows the field dependence of the creep rate. In low fields, S decreases as H increases, a trend that reverse above ~0.5 T. This change in behavior may be related to a different source of vortex pinning at low than at high fields. It roughly coincides with the low-field change in shape of the M(H) loops around H_on ~ 0.5 T. This trend is apparent in the inset, which compares the temperature dependencies of H_on (open symbols) and the field at which the minimum in creep S(H) occurs (closed symbols). Because of this, in the following section, we will separately analyze low-field and high-field measurements. We will first present S(T) and an analysis of the vortex state in the low-field regime, and then proceed to analyze the high-field regime.

Figure 5

Field dependence of the magnetic relaxation rate at temperatures 15–40 K. Non-monotonicity is suggestive of different dynamics at low versus high magnetic fields. Inset shows the temperature dependencies of H_on (open symbols) and the field at which the minimum in creep S(H) occurs (closed symbols).

Glassy vortex dynamics and elastic-to-plastic crossovers

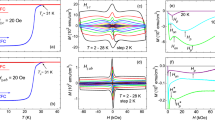
To study the dynamics in the low-field weak pinning regime, exemplified in Fig. 3(b), we measured vortex creep for μ₀H < 0.5 T, shown in the main panel of Fig. 6(a). The creep rates in fields of 0.1–0.3 T are similar over the entire temperature range, plateauing at S ~ 0.06 for T < 40 K then sharply rising at higher temperatures. Such behavior is akin to S(T) in YBCO samples, which typically exhibit a plateau around S ~ 0.02–0.035^19,52,53. In YBCO, the plateau appears because ${U}_{0}\ll \mu T\,\mathrm{ln}(t/{t}_{0})$ such that $S \sim {[\mu {k}_{B}\mathrm{ln}(t/{t}_{0})]}^{-1}$ becomes T-independent. It is often associated with glassy vortex dynamics because μ ≈ 1 considering S ~ 0.035 and ln(t/t₀) ≈ 27 for a typical measurement window of t ~ 1 hour^19,53.

Figure 6

Temperature dependence of the vortex creep rate in applied magnetic fields of (a) 0.1–0.4 T and (c) 0.7–5 T. The inset to (a) shows the energy scale U^* ≡ k_BT/S versus 1/J. The lines are linear fits to the data for temperatures 5–25 K, and the slopes yield the glassy exponents μ ≈ 1 at 0.4 T and μ ≈ 0.5 for 0.1–0.3 T. (b) Magnetization (M) collected every ~15 s for 67 hours at 20 K and 0.3 T. The black curve is a fit to Eq. (5) using μ = 0.5, where J(t) ∝ M(t). (d) Energy scale U^* plotted against 1/J for applied field 0.7–1.8 T. The lines are linear fits, and the change from a positive to negative slope suggests a crossover from elastic vortex dynamics to plastic flow at H_cr. The dashed lines show examples of how the glassy exponents μ, displayed in the phase diagram in Fig. 7(a), were extracted.

Similarly, for our Hg1201 sample, if ${U}_{0}\ll \mu {k}_{B}T\,\mathrm{ln}(t/{t}_{0})$ were true, the S ~ 0.05 plateau would yield μ ~ 0.6. However, in our sample, we do not yet know the comparative magnitudes of U₀ and μk_BTln(t/t₀). To extract μ without the need for assumptions regarding U₀, it is common practice^{37,54,55,56,57,58} to define an experimentally accessible auxiliary energy scale U^* ≡ k_BT/S. From Eq. (6), we see that U^* = U₀ + μk_BTln(t/t₀) and, combined with Eq. (5), find that

$${U}^{\ast }\equiv \frac{{k}_{B}T}{S}={U}_{0}{\left(\frac{{J}_{c0}}{J}\right)}^{\mu }.$$

(7)

Hence, μ can be directly obtained from the slope of U^* versus 1/J on a log − log plot. As shown in the Fig. 6(a) inset, μ = 0.5 for fields of 0.1–0.3 T. We reinforce this result with a complementary 67 hour long relaxation study shown in Fig. 6(b) and fitting the resulting M(t) to the interpolation formula Eq. (5). For free parameters J_c0, U₀, and μ, the best fit again produces μ = 0.5, which is expected for collective creep of large bundles of 2D pancake vortices (see Table 1)⁵⁹.

The presence of large bundles in these small fields is suggestive of a clean pinning landscape in which long-range 1/r vortex-vortex interactions are only weakly perturbed by vortex-defect interactions. Furthermore, this result is consistent with the evidence from H_irr(T) (shown in Fig. 4) of a 2D vortex state over a wide low temperature $T/{T}_{c}\ll 0.6$ region of the phase diagram. We have now ascertained that, though the plateau in S(T) appears at a higher S than in YBCO, it again correlates with glassiness.

At 0.4 T, S(T) is non-monotonic, reaching a local minimum around 30 K (see Fig. 6(a)). As shown in the Fig. 6(a) inset, we extract μ ≈ 1, which is close to the μ = 13/16 expectation for creep of medium bundles of pancake vortices (see Table 1). So, the system transitions from creep of large bundles at low fields μ₀H < 0.4 T to medium bundles at 0.4 T. This change in μ occurs roughly around H_on (compare to Fig. 3(b)) and the minimum in S(H) (compare to Fig. 5). In many systems, the bundle size increases with increasing H⁵¹. Hence, this scenario is not standard, but is consistent with our suspected mechanism for H_on: as H increases, the strength of pinning suddenly increases around H_on causing the lattice to become more entangled, the bundle size to decrease, and we see both J_c and μ increase.

Collective creep theory only considers elastic deformations of the vortex lattice and neglects dislocations. At high temperatures and/or fields, the elastic pinning barrier becomes quite high and plastic deformations of the vortex lattice can become more energetically favorable. Plastic creep⁶⁰ involves the motion of a channel of vortices constrained between two edge dislocations of opposite sign (dislocation pairs) and requires surmounting a diverging plastic barrier U_pl ~ J^−μ for small driving force $J\ll {J}_{c0}$. It manifests as a negatively sloped region in a U^*(1/J) plot: in Eq. 7, μ < 0 is conventionally represented using the notation p, such that the auxiliary quantity U^* scales as U₀(J_c0/J)^p in the plastic regime. Note that the true potential barrier U(J) in Eq. (4) remains monotonically decreasing with increasing current.

Figure 6(c) displays creep rates at fields H > 0.5 T. Representing the data as U^*(1/J), plotted in Fig. 6(d), the slopes exhibit a distinct sign change, revealing elastic (μ > 0) to plastic (μ < 0 → p) crossovers for H ≤ 2 T. Figure 6(d) displays the 1 T data for fields of 0.7–1.8 T. From the data, we extract the exponents μ displayed in the vortex phase diagram show in Fig. 7(a). We see, for example, that at 1 T the sample hosts creeping small bundles of pancake vortices in the elastic regime T < 20. To investigate the dynamics at the crossover temperature T_cr = 20 K, we perform a 6-hour measurement of M(t) that is plotted in the Fig. 7(b) and fit the data to Eq. (5). To reduce the number of free parameters (J_c0 and U₀), we obtain μ from the slope of 1/S plotted against lnt, see Eq. (6) and the Fig. 7(b) inset. Clearly, the early stages of relaxation is glassy. The bundle size evolves over time, manifesting as a change in μ. In the latter stages, we observe a transition to plastic flow.

Figure 7

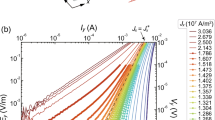
(a) Vortex phase diagram determined from creep measurements overlaid with position of second magnetization peak. (b) 1/S versus lnt determined from the time-dependent magnetization M(t) data shown in the inset. M(t) was collected every ~15 s for 6 hours at 20 K and 1 T, at the elastic-to-plastic crossover. The data points in the main panel represent S extracted from subsets of the data over intervals Δt. Dashed lines are linear fits. The red, green, and blue curves in the inset are fits to Eq. (5), where J(t) ∝ M(t), using μ = 0.9, μ = 0.5, and μ → p = −0.3, respectively. (c) Upper branch of M(H) loop at T = 20 K constructed from magnetic relaxation data, where M(t_i) represents the magnetization a time t_i after the critical state was formed. The inset demonstrates the extraction technique and how the first measurement collected by the magnetometer occurs at approximately t_i = 100 s.

Discussion

Elastic-to-plastic crossovers are considered the cause of the second magnetization peak in many superconductors^32,37,38,40. However, the origin of the SMP in Hg1201 is controversial. Daignère et al.^43,61 found no correlation between the SMP and elastic-to-plastic crossovers in Hg1201 single crystals, and concluded that the SMP merely arises from competition between an increase in J_c and decrease in pinning energy with increasing magnetic field. On the contrary, Pissas et al.⁴⁴ showed that though H_cr < H_smp, a correlation between the two fields does indeed exist, therefore the peak is possibly associated with collective-to-plastic transitions. That study reconciled the lack of coincidence between the two fields as caused by very fast creep at low fields and slower creep at high fields. To understand their reasoning, it is important to note that magnetization measurements are not collected instantaneously with the application of a magnetic field. That is, there is a 10−100 s lag between establishing the field and measuring M due to the time required for setting the magnet in persistent mode and translating the sample through the magnetometer SQUID detection coils. Consequently, by the time M is recorded during magnetization loop measurements, J is much less than J_c0 at low fields where creep is fast and closer to J_c0 at higher fields where creep is slow. This idea was further supported by a demonstration that measuring the loop faster shifts H_smp to lower fields, towards H_cr⁴⁴.

To explore this issue, we overlay our measurements of H_smp and H_cr in the phase diagram in Fig. 7(a). Figure 6(d) show examples of how H_cr was extracted from U^*(1/J). At low temperatures T/T_c < 0.2, the appearance of the SMP coincides with the elastic-to-plastic crossover whereas H_cr < H_smp at higher temperatures. Given this discrepancy, we now consider the previous argument that fast creep rates make measurements of H_smp from loops inaccurate.

As described above, we typically create a magnetization loop by measuring M once at each field as the field is ramped up in steps. Constructing the loop instead from magnetic relaxation data enables us to set a consistent time scale for all M values. We achieve this by extracting M from a linear fit to logM − logt at a predetermined time t_i after formation of the critical state, exemplified in the inset to Fig. 7(c). This also allows us to estimate M before the first measurement. The main panel shows how M(H) changes with t_i. We find that a faster measurement increases H_smp, moving it away from H_cr, contrary to the observation in Pissas et al.⁴⁴.

Conversely, the time scale associated with our determination of the elastic-to-plastic crossover is arguably the 1 hour duration of our creep measurements, therefore, an appropriate comparison requires H_smp to be determined from t_i = 1 hour. As shown in Fig. 7(a,c), though this reduces H_smp, it remains significantly larger than H_cr. We can therefore conclude that the elastic-to-plastic crossover is not the source of the SMP at high temperatures. The SMP could be caused by a transition in the structure of the vortex lattice. As the conditions for this transition would depend on anisotropy, this could be clarified through a comprehensive study comparing magnetization in Hg1201 crystals having different anisotropies, achieved by varying the doping, or through neutron scattering studies⁴⁷.

To summarize, we have studied the field- and temperature- dependent magnetization and vortex creep in an HgBa₂CuO_4+δ single crystal to understand the effects of anisotropy on vortex dynamics in superconductors. We reveal glassy behavior involving collective creep of bundles of 2D pancake vortices over a broad range of temperatures and fields as well as temperature- and time-tuned crossovers from elastic dynamics to plastic flow. The isothermal magnetization loops exhibit distinct second magnetization peaks that have also been observed in previous studies of Hg1201, and H_smp(T) decays exponentially at low temperatures then exhibits an abrupt change in behavior above T/T_c = 0.5. The origin of the second magnetization peak in superconductors can be controversial, and is often attributed to an elastic-to-plastic crossover. Here we clearly show that the second magnetization in Hg1201 is not caused by an elastic-to-plastic crossover at T/T_c > 0.2 and occurs within the plastic flow regime.

Methods

Hg1201 single crystals were grown using an encapsulated self-flux method⁶² at Los Alamos National Laboratory. The crystals were subsequently heat-treated at 350 °C in air and quenched to room temperature to achieve near optimal doping⁶. The high-quality of the synthesized crystals is evinced by the observation of large quantum oscillations in other samples from the same growth batch. Multiple crystals were measured to verify reproducibility. The results presented in this manuscript were collected on a crystal with dimensions 1.28 × 0.84 × 0.24 mm³ and mass of 1.9 mg, shown in the Fig. 1(a) inset.

All measurements were performed using a Quantum Design superconductor quantum interference device (SQUID) magnetometer equipped with two independent sets of detection coils to measure the magnetic moment in the direction of (m_L) and transverse to (m_T) the applied magnetic field. For measurements requiring manipulating the field orientation, the crystal was placed on a rotating sample mount. Most measurements, however, were conducted with the field aligned with the sample c-axis (H||c), in which case the sample was mounted on a delrin disk inside a straw.