Introduction

The limit equilibrium approach is commonly used in engineering applications for evaluating slope stability1,2,3. As algorithms have advanced in sophistication, scholars have increasingly and more productively studied the stability of three-dimensional (3D) slopes. Canonically, the sliding body is divided into vertical columns, and under the assumption of inter-column forces, different 3D limit equilibrium methods are developed for the 3D slope safety factor by different force and moment balance conditions. For example, Hovland4, Hungr5, and Boutrup6 extended the two-dimensional (2D) model developed by Fellenius, Bishop and Janbu to 3D, but such methods need to assume inter-column forces, and their iterative calculations may not converge7.

Therefore, scholars proposed to improve the limit equilibrium methods by assuming the normal stress distribution acting on the slip surface. Assuming a normal stress distribution, Bell8 and Zhu and Lee9 proposed that the normal stress distribution acting on the slip surface be considered a function with two parameters that need to be determined. Zhu10,11 and Zheng12 proposed that the normal stress distribution acting on the slip surface was composed of an initial function and a correction function, and the correction function was assumed to be a linear interpolation function with two parameters to be determined. This method does not need to assume the inter-column forces, and compensates for flaws in the integration of calculations in conventional methods; however, these assumed functions cannot effectively simulate the actual normal stress distribution acting on the slip surface, which leads to inaccurate computational results7.

At the same time, although many commercial software applications using the 3D limit equilibrium method (3D-LEM) have also been developed, the data formats for these applications are different, making them inconvenient for engineers to use, which is not conducive to secondary development. Therefore, geographic information systems (GIS) technology having powerful spatial data processing capability was introduced into the 3D slope stability analysis13. GIS can provide a uniform platform and data structure for spatial computing problems. All the data related to slope can be expressed in a raster dataset based on the grid column unit, which makes data processing and calculation more convenient. Therefore, the 3D slope stability analysis model can be established based on grid column units.

Studies have investigated the combination of GIS and mechanical model. The Current Study14,15,16 extended the 2D Hovland model, Bishop Model and Janbu model to 3D models; we developed 3D slope stability analysis software based on GIS, called 3Dslope. Mergili17 combined GRASS GIS and the 3D Hovland model to implement a 3D Slope stability model which can accommodate both shallow and deep-seated slope failures. The above mechanical models were combined mainly with GIS by assuming inter-column forces. However, the establishment of 3D-LEM based on the assumed normal stress distribution acting on the slip surface in GIS has not been studied by scholars, and its algorithm is very different from the above mechanical models. The key to this method is in its assumption about the normal stress distribution acting on the slip surface based on GIS. The accuracy of measurements using the method is proportional to the reasonableness of this assumption.

This study proposes a method for analyzing stability of the 3D slope based on GIS which assumes normal stress distribution acting on the slip surface. The composition of the normal distribution of stress is evaluated and we recommend an approximation method to represent the actual normal distribution of stress acting on the slip surface. Compared with traditional methods, the resulting value calculated by using the approximation function is closer to the actual value. To make the calculation more convenient, a GIS-based extension module is developed to evaluate slope stability. This module overcomes the problem of inconsistent data format and difficulty in secondary development. The accuracy and feasibility of this method are verified by three cases.

Implementation of 3D limit equilibrium method in GIS

3D slope model based on GIS

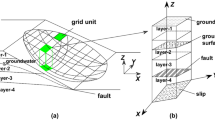
Figure 1(a) Shows a 3D sliding body divided into grid columns. Each column contains all the data related to the slope, such as surface, strata, groundwater, fault, slip, etc., as shown in Fig. 1(b). With GIS, the parameters of each column for solving the 3D safety factor can be obtained, such as elevation, inclination, slope angle, etc.

Figure 1
figure 1

3D view of landslide and one grid column. (a) 3D view of landslide. (b) 3D view of one grid column.

Full size image

Without GIS it would be a tedious and time-consuming process to measure the 3D safety factor based on a column model. However, in the GIS system, the data related to the slope can be abstracted into a vector layer by using the functions of GIS spatial analysis, and the vector layer can be converted into a grid layer, as shown in Fig. 2. The grid size (cell size) can be set appropriately to achieve the requisite precision. All grid layers in a column relating to the slope are combined to form a segment of the grid column. Based on the grid column model, the calculation of the 3D safety factor will be routine and canonical.

Figure 2
figure 2

GIS layers for slope stability analysis.

Full size image

To facilitate subsequent calculations, the XOY coordinate system was converted to an X′CY′ coordinate system. The X′-axis direction was defined as the sliding direction of the landslide. The right-hand rule determined the positive directions of the Y′- and Z-axes. In addition, point O, i.e., the origin of the XOY coordinate system, was translated to point C in the X′CY′ coordinate system, as shown in Fig. 3. The transformation of the coordinates can be expressed as follows:

$$\{\begin{array}{c}x{\prime} \\ y{\prime} \end{array}\}=(\begin{array}{c}\cos (90-\beta )\,\sin (90-\beta )\\ -\,\sin (90-\beta )\,\cos (90-\beta )\end{array})\{\begin{array}{c}x-{x}_{0}\\ y-{y}_{0}\end{array}\}$$
(1)

where β is the sliding direction of the landslide, defined as the main dip direction of the landslide. The main dip direction of the landslide is the most frequent value of the dip directions of all grid columns. x′ and y′ are the coordinate values of the center of the bottom of each grid column in the X′CY′ coordinate system. x and y are the coordinate values of the center of the bottom of each grid column in the XOY coordinate system. x0 and y0 are the coordinate values of point C in the XOY coordinate system.

Figure 3
figure 3

Coordinate system conversion.

Full size image

Force analysis of one grid column

Figure 4 shows the force analysis of one grid column and its 3D spatial relationship. We can specify the forces acting on each grid column as follows:

  1. (1)

    The weight of one grid column is W; the direction is the Z-axis, and the weight acts at the centroid of the grid column.

  2. (2)

    The resultant horizontal seismic force is kW, where k is the “seismic coefficient”; the direction of kW is the X′-axis, and the resultant horizontal force acts at the centroid of the grid column.

  3. (3)

    The external loads on the ground surface are represented by P; the direction of P is the Z-axis, and these external loads act at the center of the top of the grid column.

  4. (4)

    The normal and shear stresses acting on the slip surface are represented by σ and τ, respectively. Normal stress is directed perpendicular to the slip surface; shear stress is directed in the sliding direction of the landslide. The normal and shear stresses work at the base of the grid column’s centroid.

  5. (5)

    The pore water pressure on the slip surface is u.

  6. (6)

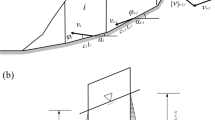
    The moment arm of P and W around the Y′-axis is dx; the moment arm of kW around the X′-axis is dy; the moment arm of σ around the Y′-axis is dσ; and the moment arm of τ around the Y′-axis is dτ, as shown in Fig. 3(a).

  7. (7)

    The horizontal tangential forces on the vertical face at y = 0 and vertical face at y = Δy (Δy represents the size of the grid column along Y-axes) are T and T + ΔT, respectively; the vertical tangential forces on the vertical face at y = 0 and vertical face at y = Δy are R and R + ΔR, respectively; the normal forces on the vertical face at y = 0 and vertical face at y = Δy are F and F + ΔF, respectively; the horizontal tangential forces on the vertical face at x = 0 and vertical face at x = Δx are E and E + ΔE, respectively; the vertical tangential forces on the vertical face at x = 0 and vertical face at x = Δx are V and V + ΔV, respectively; and the normal forces on the vertical face at x = 0 and vertical face at x = Δx are H and H + ΔH, respectively, as shown in Fig. 3(b).

  8. (8)

    θ is the dip of the grid column on the slip surface; α is the dip direction of the grid column on the slip surface; θr is the apparent dip of the main inclination direction of the landslide; ax is the apparent dip of the X-axis; and ay is the apparent dip of the Y-axis, as shown in Fig. 3(c).

Figure 4
figure 4

Force analysis of one grid column and the 3D spatial relationship. (a,b) Show the force analysis of one grid column in the 2D and 3D views of the slope, respectively, and (c) shows the spatial relationship in the 3D view of the slope.

Full size image

3D limit equilibrium equations based on GIS

As with many other limit equilibrium methods, the safety factors for each grid column on its respective slip surfaces are assumed to be equal. The 3D safety factor is derived from the Mohr-Coulomb strength criterion as follows:

$$S{F}_{3D}=\frac{c{\prime} +\sigma \,\tan \varphi {\prime} }{\tau }$$
(2)

where SF3D is the 3D safety factor, φ′ is the effective friction angle, and c′ is the effective cohesion.

As shown in Fig. 4, for the entire 3D sliding body, the total intercolumn force in the X′, Y′, and Z directions and the total moment around the Y′-axis are zero. Therefore, the force equilibrium equations in the X′, Y′ and Z directions and moment equilibrium equation around the Y′-axis become

$$X{\prime} =\sum _{I}\sum _{J}\{A\tau \,\cos \,{\theta }_{r}-A(\sigma +u)\sin \,\theta \,\cos (\alpha -\beta )-kW\}=0$$
(3)
$$Y{\prime} =\sum _{I}\sum _{J}A(\sigma +u)\sin \,\theta \,\sin (\alpha -\beta )=0$$
(4)
$$Z=\sum _{I}\sum _{J}(A\tau \,\sin \,\theta r+A(\sigma +u)\cos \,\theta -W-P)=0$$
(5)
$$M=\sum _{I}\sum _{J}\{(W+P){d}^{x}+kW{d}^{y}-(\sigma +u){d}^{\sigma }-A\tau \,\cos (\alpha -\beta ){d}^{\tau }\}=0$$
(6)

where

$${d}^{x}=x{\prime} ,{d}^{y}=0.5\,h+z$$
(7)
$${d}^{\sigma }=(x{\prime} -z\,\tan \,\theta r)\cos \,\theta r$$
(8)
$${d}^{\tau }=(x{\prime} -z\,\tan \,\theta r)\sin \,\theta r+\frac{z}{\cos \,\theta r}$$
(9)
$$W=cellsiz{e}^{2}\mathop{\sum }\limits_{i=1}^{n}hi\gamma i,P=cellsiz{e}^{2}p,u=\frac{D}{\cos \,\theta }$$
(10)

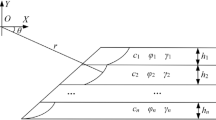
where I and J represent the numbers of rows and columns of the grid, respectively; z represents the coordinate values of the center of the bottom of each grid column; h is the height of the grid column; hi is the height of each stratum; and γi is the natural unit weight of each stratum; D is the distance from the center of the bottom of the grid column to the water surface.

From Fig. 3(c), the apparent dips of the X-axis and Y-axis are

$$\tan \,{a}_{x}=\,\cos \,\alpha \,\tan \,\theta ,\,\tan \,{a}_{y}=\,\sin \,\alpha \,\tan \,\theta $$
(11)

The slip surface area of one grid column is calculated by

$$A=cellsiz{e}^{2}\left[\frac{\sqrt{(1-{\sin }^{2}{a}_{x}{\sin }^{2}{a}_{y})}}{\cos \,{a}_{x}\,\cos \,{a}_{y}}\right]$$
(12)

The apparent dip of the landslide’s main inclination direction is determined by:

$$\tan \,{\theta }_{\gamma }=\,\tan \,\theta |\cos (\alpha -\beta )|$$
(13)

When combining Eqs. (2–6), the equation set is established to solve the 3D safety factor. Since the equation set includes (I × J + 1) unknowns, i.e., SF3D, and (I × J) normal stresses σ, the equation set cannot be solved. If the normal stress distribution on the slip surface is known, this equation set can be solved.

Analysis of the Composition of Normal Stress Distribution σ

As shown in Fig. 4(b), the force balance equation for the X′-, Y′- and Z-axes can be obtained according to the limit equilibrium condition of a single grid column and without any assumption on force as follows:

$$X{\prime} =A\tau \,\cos \,{\theta }_{r}-A(\sigma +u)\sin \,\theta \,\cos (\alpha -\beta )-kW+\Delta T-\Delta H=0$$
(14)
$$Y{\prime} =A(\sigma +u)\sin \,\theta \,\sin (\alpha -\beta )+\Delta F-\Delta E=0$$
(15)
$$Z=A\tau \,\sin \,\theta r+A(\sigma +u)\cos \,\theta -W-P+\Delta V-\Delta R=0$$
(16)

Subtracting τ from Eqs. (14–16) allows the expression of the normal stress distribution function on the slip surface to be obtained as

$$\begin{array}{rcl}\sigma & = & \frac{(W+P)\cos \,\theta r(\sin \,\beta +\,\cos \,\beta )-kW\,\sin \,\theta r}{A\,\cos \,\theta \,\cos \,\theta r(\sin \,\beta +\,\cos \,\beta )+A\,\sin \,\theta \,\sin \,\theta r(\sin \,\alpha +\,\cos \,\alpha )}-u\\ & & +\frac{(\Delta V-\Delta R)\cos \,\theta r(\sin \,\beta +\,\cos \,\beta )-(\Delta T-\Delta H+\Delta F-\Delta E)\sin \,\theta r}{A\,\cos \,\theta \,\cos \,\theta r(\sin \,\beta +\,\cos \,\beta )+A\,\sin \,\theta \,\sin \,\theta r(\sin \,\alpha +\,\cos \,\alpha )}\end{array}$$
(17)

Using Eq. (17), we conclude that the normal stress distribution σ acting on the slip surface can be divided into two parts. The first part comes from the weight W, external loads P, the pore water pressure u, and the resultant horizontal seismic force kW, and is recorded as σ1; the other part comes from the inter-column forces, and is recorded as σ2. Equation (17) can be simplified as

$$\sigma =\sigma 1+\sigma 2$$
(18)

where

$${\sigma }_{1}=\frac{(W+P)\cos \,\theta r(\sin \,\beta +\,\cos \,\beta )-kW\,\sin \,\theta r}{A\,\cos \,\theta \,\cos \,\theta r(\sin \,\beta +\,\cos \,\beta )+A\,\sin \,\theta \,\sin \,\theta r(\sin \,\alpha +\,\cos \,\alpha )}-u$$
(19)
$${\sigma }_{2}=\frac{(\Delta V-\Delta R)\cos \,\theta r(\sin \,\beta +\,\cos \,\beta )-(\Delta T-\Delta H+\Delta F-\Delta E)\sin \,\theta r}{A\,\cos \,\theta \,\cos \,\theta r(\sin \,\beta +\,\cos \,\beta )+A\,\sin \,\theta \,\sin \,\theta r(\sin \,\alpha +\,\cos \,\alpha )}$$
(20)

If the slip surface is known, the parameters in Eq. (19) are known; therefore, σ1 belongs to the known function. Since the distribution of the inter-column forces cannot be accurately determined, σ2 belongs to the unknown function.

In our work18, the following conclusions can be drawn concerning the normal distribution of stresses on the slip surface: (1) in the composition of the normal slip surface stress distribution, the ratio of the weight, external force, the pore water pressure, and the resultant horizontal seismic force (σ1) to the normal stress (σ) is high, while the ratio of the inter-column forces (σ2) to the normal stress (σ) is low; and (2) the normal stresses σ, σ1 and σ2 are continuous and smooth curves.

Construction of the Normal Stress Distribution σ(x′, y′)

In Fig. 5(a), point C is the centroid of the landslide. The direction of the long axis, indicated by nm, is the sliding direction of the landslide. Points n and m are the vertex point and the lowest point of the landslide area, respectively. The direction of the shorter axis, indicated by FR, is perpendicular to the sliding direction of the landslide. AA and BB show the size feature of the landslide. By taking two points (x = m1 and x = m2) in the direction of the X′-axis, the total normal stresses can be determined, as shown in Fig. 5(c). These two points are chosen as follows:

$${m}_{1}=m+1/3(n-m)$$
(21)
$${m}_{2}=m+2/3(n-m)$$
(22)
Figure 5
figure 5

Construction of the normal stress distribution on the slip surface.

Full size image

Normal stress distribution σ(x′) along the sliding direction of the landslide

According to Eq. (18), the normal stress distribution along the sliding direction of the landslide can be obtained as follows:

$$\sigma (x{\prime} )=\sigma 1(x{\prime} )+\sigma 2(x{\prime} )$$
(23)

where σ(x′) represents the normal stress distribution acting on the slip surface along the sliding direction of the landslide. σ1(x′) represents the component of the weight, external force, and the resultant horizontal seismic force in σ(x′), which can be determined by the formula in Eq. (19). σ2(x′) represents the component of the inter-column forces in σ(x′).

If the slip surface is known, σ1(x′) is a known function, and σ2(x′) is an unknown function. The unknown function can be considered to approximate the expression of σ2(x′) using an approximation function. Since σ2(x′) accounts for a small portion of σ(x′), the approximation function has little effect on the value of σ(x′), making σ(x′) close to the actual normal stress distribution.

Assuming that the approximation function is β(x′), the normal stress distribution σ(x′) along the sliding direction of the landslide can be expressed as follows:

$$\sigma (x{\prime} )={\sigma }_{1}(x{\prime} )+\beta (x{\prime} )$$
(24)

Based on the research of Zhu9 and Yu18, the approximation function β(x′) is assumed to be a Lagrange polynomial of degree 3; that is,

$$\beta (x{\prime} )={k}_{1}{g}_{1}(x{\prime} )+{k}_{2}{g}_{2}(x{\prime} )+{g}_{3}(x{\prime} )$$
(25)

where

$${g}_{1}(x{\prime} )=\frac{(x{\prime} -m)(x{\prime} -n)(x{\prime} -{m}_{2})}{({m}_{1}-m)({m}_{1}-n)({m}_{1}-{m}_{2})}$$
(26)
$${g}_{2}(x{\prime} )=\frac{(x{\prime} -m)(x{\prime} -n)(x{\prime} -{m}_{1})}{({m}_{2}-m)({m}_{2}-n)({m}_{2}-{m}_{1})}$$
(27)
$${g}_{3}(x{\prime} )={\beta }_{m}\frac{(x{\prime} -n)(x{\prime} -{m}_{1})(x{\prime} -{m}_{2})}{(m-n)(m-{m}_{1})(m-{m}_{2})}+{\beta }_{n}\frac{(x{\prime} -n)(x{\prime} -{m}_{1})(x{\prime} -{m}_{2})}{(n-m)(n-{m}_{1})(n-{m}_{2})}$$
(28)

where k1 and k2 are dimensionless variables; βm and βn are the normal stresses acting on the lowest point and the vertex point of the slip surface, respectively.

Since the normal stress at the boundary of the upper half of the landslide is very low, it can reasonably be assumed that the normal stresses at the boundary of the upper half of the landslide are zero19 and that βn = 0. In addition, the normal stresses at the boundary of the bottom half of the landslide are expressed as σmx′/m, as shown in Fig. 5(b). βm is calculated as follows:

$${\beta }_{m}=\sigma (m)-{\sigma }_{1}(m)$$
(29)

Normal stress distribution σ(y′) perpendicular to the sliding direction of the landslide

In the direction perpendicular to the sliding direction of the landslide, the normal stress distribution σ(y′) is approximated by a parabola along the sliding direction of the landslide, and the apex of the parabola falls on σ(x′)18. Since the apex of the parabola falls on σ(x′) and the normal stress σ(x′) is close to the actual normal stress distribution, the accuracy of the function σ(y′) is controlled. σ(y′) can be described by

$${\sigma }_{b}(y{\prime} )={h}_{1}{y{\prime} }^{2}+{h}_{2}y{\prime} +{h}_{3}$$
(30)
$${\sigma }_{u}(y{\prime} )={\lambda }_{1}{y{\prime} }^{2}+{\lambda }_{2}y{\prime} +{\lambda }_{3}$$
(31)

where σb(y′) is the normal stress σ(y′) acting on the bottom half of the landslide; σu(y′) is the normal stress σ(y′) acting on the upper half of the landslide; and h1, h2, h3, λ1, λ2 and λ3 are dimensionless variables.

As shown in Fig. 5(b,d), combined with the characteristics of the parabolic equation, the following can be obtained:

$$h1={(A{{A}_{x{\prime} }}^{2})}^{-1}\left(\frac{x{\prime} \sigma (m)}{m}-\sigma (x{\prime} )\right),\,{h}_{2}=0,\,{h}_{3}=\sigma (x{\prime} )$$
(32)
$$\lambda 1=-\,{(A{{A}_{x{\prime} }}^{2})}^{-1}\sigma (x{\prime} ),\,{\lambda }_{2}=0,\,{\lambda }_{3}=\sigma (x{\prime} )$$
(33)

where AAx′ is the shorter axis size corresponding to the abscissa.

Normal stress distribution σ(x′, y′)

After substituting Eqs. (24), (32,33) into Eqs. (30,31), the normal stress distribution σ(x′, y′) can be determined:

$$\{\begin{array}{c}{\sigma }_{b}(x{\prime} ,y{\prime} )={(A{{A}_{x{\prime} }}^{2})}^{-1}{y{\prime} }^{2}\left\{\frac{\sigma (m)}{m}x{\prime} -({\sigma }_{1}(x{\prime} )+\beta (x{\prime} ))\right\}+{\sigma }_{1}(x{\prime} )+\beta (x{\prime} )\\ {\sigma }_{u}(x{\prime} ,y{\prime} )=\{1-{(A{{A}_{x{\prime} }}^{2})}^{-1}{y{\prime} }^{2}\}({\sigma }_{1}(x{\prime} )+\beta (x{\prime} ))\end{array}$$
(34)

where σb(x′, y′) is the normal stress acting on the bottom half of the landslide, and σu(x′, y′) is the normal stress acting on the upper half of the landslide.

The normal stress distribution σ(x′, y′) containing three unknowns (k1, k2 and σ(m)) is determined by substituting Eq. (25) into Eq. (34).

Solving the 3D Safety Factor

The equation set for calculating the 3D slope safety factor is obtained by substituting Eqs. (2) and (34) into Eqs. (3–6). Now, having four available equations and four unknowns (SF3D, k1, k2 and σ(m)), these equations can be solved simultaneously by the Newton-Raphson method.

First, a set of initial values (SF3D0, k10, k20 and σ(m)0) is applied to obtain four nonzero values: ΔX′, ΔY′, ΔZ and ΔM. Next, this process is repeated until the four nonzero values approach zero. The values for SF3D, k1, k2 and σ(m) in l iterations are determined as follows:

$$S{{F}_{3D}}^{l+1}=S{{F}_{3D}}^{l}-{L}_{SF3D}/D$$
(35)
$${{k}_{1}}^{l+1}={{k}_{1}}^{l}-{L}_{k1}/D$$
(36)
$${{k}_{2}}^{l+1}={{k}_{2}}^{l}-{L}_{k2}/D$$
(37)
$$\sigma {(m)}^{l+1}=\sigma {(m)}^{l}-{L}_{\sigma (m)}/D$$
(38)

where

$$\begin{array}{c}D=|\begin{array}{c}\frac{\partial X{\prime} }{\partial S{F}_{3D}}\,\frac{\partial X{\prime} }{\partial {k}_{1}}\,\frac{\partial X{\prime} }{\partial {k}_{2}}\,\frac{\partial X{\prime} }{\partial \sigma (m)}\\ \frac{\partial Y{\prime} }{\partial S{F}_{3D}}\,\frac{\partial Y{\prime} }{\partial {k}_{1}}\,\frac{\partial Y{\prime} }{\partial {k}_{2}}\,\frac{\partial Y{\prime} }{\partial \sigma (m)}\\ \frac{\partial Z}{\partial S{F}_{3D}}\,\frac{\partial Z}{\partial {k}_{1}}\,\frac{\partial Z}{\partial {k}_{2}}\,\frac{\partial Z}{\partial \sigma (m)}\\ \frac{\partial M}{\partial S{F}_{3D}}\,\frac{\partial M}{\partial {k}_{1}}\,\frac{\partial M}{\partial {k}_{2}}\,\frac{\partial M}{\partial \sigma (m)}\end{array}|,\,LS{F}_{3D}=|\begin{array}{c}\Delta X{\prime} \,\frac{\partial X{\prime} }{\partial {k}_{1}}\,\frac{\partial X{\prime} }{\partial {k}_{2}}\,\frac{\partial X{\prime} }{\partial \sigma (m)}\\ \Delta Y{\prime} \,\frac{\partial Y{\prime} }{\partial {k}_{1}}\,\frac{\partial Y{\prime} }{\partial {k}_{2}}\,\frac{\partial Y{\prime} }{\partial \sigma (m)}\\ \Delta Z\,\frac{\partial Z}{\partial {k}_{1}}\,\frac{\partial Z}{\partial {k}_{2}}\,\frac{\partial Z}{\partial \sigma (m)}\\ \Delta M\,\frac{\partial M}{\partial {k}_{1}}\,\frac{\partial M}{\partial {k}_{2}}\,\frac{\partial M}{\partial \sigma (m)}\end{array}|,\\ {L}_{k1}=|\begin{array}{c}\frac{\partial X{\prime} }{\partial S{F}_{3D}}\,\Delta X{\prime} \,\frac{\partial X{\prime} }{\partial {k}_{2}}\,\frac{\partial X{\prime} }{\partial \sigma (m)}\\ \frac{\partial Y{\prime} }{\partial S{F}_{3D}}\,\Delta Y{\prime} \,\frac{\partial Y{\prime} }{\partial {k}_{2}}\,\frac{\partial Y{\prime} }{\partial \sigma (m)}\\ \frac{\partial Z}{\partial S{F}_{3D}}\,\Delta Z\,\frac{\partial Z}{\partial {k}_{2}}\,\frac{\partial Z}{\partial \sigma (m)}\\ \frac{\partial M}{\partial S{F}_{3D}}\,\Delta M\,\frac{\partial M}{\partial {k}_{2}}\,\frac{\partial M}{\partial \sigma (m)}\end{array}|,\,Lk2=|\begin{array}{c}\frac{\partial X{\prime} }{\partial S{F}_{3D}}\,\frac{\partial X{\prime} }{\partial {k}_{1}}\,\Delta X{\prime} \,\frac{\partial X{\prime} }{\partial \sigma (m)}\\ \frac{\partial Y{\prime} }{\partial S{F}_{3D}}\,\frac{\partial Y{\prime} }{\partial {k}_{1}}\,\Delta Y{\prime} \,\frac{\partial Y{\prime} }{\partial \sigma (m)}\\ \frac{\partial Z}{\partial S{F}_{3D}}\,\frac{\partial Z}{\partial {k}_{1}}\,\Delta Z\,\frac{\partial Z}{\partial \sigma (m)}\\ \frac{\partial M}{\partial S{F}_{3D}}\,\frac{\partial M}{\partial {k}_{1}}\,\Delta M\,\frac{\partial M}{\partial \sigma (m)}\end{array}|,\\ {L}_{\sigma (m)}=|\begin{array}{c}\frac{\partial X{\prime} }{\partial S{F}_{3D}}\,\frac{\partial X{\prime} }{\partial {k}_{1}}\,\frac{\partial X{\prime} }{\partial {k}_{2}}\,\Delta X{\prime} \\ \frac{\partial Y{\prime} }{\partial S{F}_{3D}}\,\frac{\partial Y{\prime} }{\partial k1}\,\frac{\partial Y{\prime} }{\partial {k}_{2}}\,\Delta Y{\prime} \\ \frac{\partial Z}{\partial S{F}_{3D}}\,\frac{\partial Z}{\partial k1}\,\frac{\partial Z}{\partial {k}_{2}}\,\Delta Z\\ \frac{\partial M}{\partial S{F}_{3D}}\,\frac{\partial M}{\partial {k}_{1}}\,\frac{\partial M}{\partial {k}_{2}}\,\Delta M\end{array}|\end{array}$$
(39)

In an iterative calculation, the final convergence condition is:

$$\begin{array}{c}|{\varepsilon }_{1}|=(S{{F}_{3D}}^{l+1}-S{{F}_{3D}}^{l})/S{{F}_{3D}}^{l} < 0.001\\ |{\varepsilon }_{2}|=({{k}_{1}}^{l+1}-{{k}_{1}}^{l})/{{k}_{1}}^{l} < 0.001\\ |{\varepsilon }_{3}|=({{k}_{2}}^{l+1}-{{k}_{2}}^{l})/{{k}_{2}}^{l} < 0.001\\ |{\varepsilon }_{4}|=(\sigma {(m)}^{l+1}-\sigma {(m)}^{l})/\sigma {(m)}^{l} < 0.001\end{array}\}$$
(40)

Computational Implementation

An extension module for slope stability evaluation has been developed in GIS, and Fig. 6 illustrates the computational process.

Figure 6
figure 6

Computational process for 3D slope safety factor.

Full size image

Case Studies

Case 1: a homogeneous slope

Figure 7 shows a homogeneous slope, with slope angle β = 45°, OA = OB, and slope height H = 40 m. The unit weight is γ = 22 kN/m³, the effective friction angle is φ′ = 30°, and the effective cohesion is c′ = 30 kPa. Point O is the center of the sliding surface. The slip surface of the case is known. The sizes of grid unit can be set arbitrarily.

Figure 7
figure 7

Case 1.

Full size image

The calculation results are shown in Table 1, and the following conclusions can be drawn. 1) The 3D safety factors using the proposed method are similar to those calculated by the 3D M-P method7 and Xie’s three GIS-based models14,15,16, i.e., the 3D Hovland model, the 3D Bishop model and the 3D Janbu model. The feasibility of the proposed method is illustrated. 2) Except for the proposed method, the above four methods calculate the safety factor by assuming the inter-column forces, so the obtained safety factor is relatively small relative to the actual value, and the 3D M-P method is closest to the actual value7. The result of the proposed method is close to the 3D M-P method, and is 2.7% to 4.5% larger than the 3D M-P method, which is consistent with the pattern that the result value of the 3D M-P method is relatively small relative to the actual value. This result provides more proof that assuming the normal distribution of stress acting on the slip surface of the proposed method is close to the actual normal distribution of stresses.

Table 1 The 3D safety factor for Case 1.
Full size table

Case 2: slope with a weak layer

Figure 8 shows a slope with a weak layer sandwiched between two hard, rigid strata. In the soil, the effective cohesion of each of the three layers is 29.4 kPa, 9.8 kPa and 294 kPa; the respective effective friction angles for the three layers are 12°, 5° and 40°; and the unit weight of the three layers is 18.82 kN/m³. The size of the grid element is 0.5 m. In this case, Using a 3D critical slip surface, the 3D safety factor is calculated.

Figure 8
figure 8

Case 2.

Full size image

The calculation results are shown in Table 2. In Xie’s research20, a minimum 3D safety factor of 0.463 was determined after 100 iterations of a Monte Carlo simulation. Using the 3D M-P approach based on the 3D critical slip surface, a minimum 3D safety factor of 0.496 has been calculated. In this paper, using our proposed method based on the 3D critical slip surface, a higher minimum 3D safety factor of 0.513 was calculated. The outcome of this analysis is near the outcome of the 3D M-P test, and is 3.3% larger than that of the 3D M-P method. This case can draw conclusions similar to those from Case 1.

Table 2 The 3D safety factor for Case 2.
Full size table

Case 3: slope with a discontinuous layer

This case shows a slope with a discontinuous layer (Fig. 9). The effective friction angle is 20°, the unit weight is 18.84 kN/m³, and the effective cohesion is 28.7 kPa. The angle of effective friction and the effective cohesion of the discontinuous layer are 20° and 0 kPa, respectively. The slope is considered to have two possible sliding surfaces: the first sliding surface is a cyclic peripheral surface, and the second sliding surface is a nonperfect failure surface. The size of the grid unit is 0.5 m.

Figure 9
figure 9

Case 3.

Full size image

The results are presented in Table 3. The calculation result of the current method is the largest and is close to that of the M-P method. This case can draw conclusions similar to those from Case 1 and Case 2. The feasibility of the method is illustrated. The 3D safety factor for the first sliding surface is 2.328. The 3D safety factor for the second sliding surface in the cases with and without groundwater is 1.786 and 1.678, respectively. Moreover, this case considers the calculation of multiple combinations of groundwater, top vertical loads (with load width 5 m, length 10 m) and resultant horizontal forces due to earthquakes. According to Table 2, the impact of an earthquake on the safety factor is high, and the occurrence of an earthquake produces results that are among the most unfavorable combinations of factors. Considering the combinations of earthquake and top vertical loads (160 kN/m³), the safety factor is below the maximum design allowance (1.20). The case study results indicate that this module can readily be used to calculate various loads in slope design combinations.

Table 3 The safety factor for Case 3.
Full size table

Discussion

Discussion on the advantages of GIS-based slope stability analysis method

GIS provides a common platform for multi-source data, and all slope-related data can be converted to GIS raster datasets. Combined with the advantages of GIS in processing complex spatial data, the limit equilibrium method can be easily extended to three dimensions. By adding a professional model to the GIS, a three-dimensional slope stability analysis model based on grid column unit can be established to analyze the stability of the three-dimensional slope. The model has the advantages of simplicity and simple programming.

Discussion on the advantages of the approximation function

In this paper, the normal stress distribution σ(x′) along the sliding direction of the landslide is composed of σ1(x′) and β(x′), where σ1(x′) is a known function. Since the approximation function β(x′) has a small proportion in σ(x′), the approximation function has a small influence on the result value of σ(x′). For the normal stress distribution σ(y′) perpendicular to the sliding direction of the landslide, since the apex of the parabola falls on σ(x′), the accuracy of σ(x′) controls the accuracy of the function σ(y′). In general, the method proposed in this paper is different from the traditional method in that it does not need to ignore the effect of the inter-column forces, and the assumed normal stress distribution function has less influence on the result value, so the resulting value calculated by using the method proposed in this paper is closer to the actual value.

Discussion of the sliding direction of the landslide

The sliding direction of the landslide refers to the direction in which the slider body begins to slide. In the limit equilibrium method of this paper, it is necessary to establish the limit equilibrium equation and the assumed normal stress distribution function of the slip surface along the sliding direction of the landslide, as in Eqs. (3) and (25). However, before the landslide slides, the sliding direction of the landslide is unknown, so this paper assumes that the sliding direction of the landslide is the main dip direction of all the grid columns. For each grid column unit of the landslide, the dip direction of the slip surface is different, and the main dip direction is the most frequent value of the dip direction of all grid columns in the range of the sliding body.

Conclusions

This study proposes a method for analyzing stability of the 3D slope based on GIS which assumes a normal stress distribution that works on the slip surface. The 3D limit equilibrium equations to solve the 3D safety factor are derived from the grid column unit model, and the spatial representation of the calculation parameters is given in GIS.

An approximation function is proposed by analyzing the composition of normal stress distribution to approximate the actual normal stress distribution that operates on the slip surface. Compared with traditional methods, the resulting value calculated by using the approximation function is closer to the actual value. This approximation function provides a theoretical basis for the establishment of a GIS-based slope stability analysis method based on the assumption of normal slip surface stress distribution.

To assess the stability of the slope a GIS-based extension module is built. In this module, the slope data is derived directly from the GIS dataset, therefore, the module has the advantages of a uniform data format and simple data preparation process. The module can be used for multiple stratigraphic slopes as well as stability calculations under a variety of combined loads. The accuracy and feasibility of the module are verified by three typical cases.