Introduction

Femtosecond, high brightness, hard x-ray pulses generated by free-electron lasers (FELs)1,2,3,4,5 opens the door to a new frontier of high-intensity x-ray experiments in various research fields, e.g., physics, chemistry6, life7 and material sciences8. These pulses are able to encode valuable structural and dynamical information on atomic scales. Most of the hard x-ray FELs rely on the self-amplified spontaneous emission (SASE) scheme. Due to starting from electron shot-noise, SASE FELs usually provide partially temporal coherence corresponding to temporal isolated spikes9. Foreknown information about x-ray coherence time would benefit experiments focusing on ionization dynamics10, spectro-holography11, nonlinear mixing-wave experiment12, etc. Hence, a direct characterization method of the coherence time of the ultra-fast hard x-ray FEL pulse in time domain is a primary requirement in this field.

To directly measure the FEL coherence time, one straight forward way is to implement conventional optical method: autocorrelation, which is a widely used method in the optical wavelength. Typically, the radiation pulse is split into two identical pulses, one pulse is delayed by some optical mirrors and eventually the two pulses are recombined. The output interference versus delay gives the information of coherence time. Obviously, autocorrelation depends on the mirrors to generate optical delays, which limits its applicability for different photon energy ranges. Although it has been proven that a combination of laser beam splitter and mirror based optical delay can be used to implement autocorrelation to characterize the FEL coherence time in the extreme ultraviolet and soft x-ray regime13,14; for the hard x-ray pulses, due to the lack of mirrors, it is very difficult to realize autocorrelation. Experiments employing crystals as mirrors to generate an effective delay has been carried out to measure the coherence time of a monochromatized hard x-ray pulse15. However, this method cannot be implemented to SASE FEL coherence time characterization, since these crystals lead to external strong purification on the incident pulse spectrum, due to Bragg diffraction. Therefore the measured coherence time will be much longer than the intrinsic SASE FEL coherence time. Hence, currently, there is no effective method to characterize the coherence time of SASE FEL in the time domain. Meanwhile, x-ray pulse duration characterization method based on FEL dynamics has been well established16,17, in which the cross-correlation between ‘fresh’ electrons and x-rays has been used to measure the x-ray pulse length. However, since the electrons are almost ‘fresh’, the coherence information is smeared out. Inspired by this idea, we propose the method utilizing the cross-correlation between the x-rays and the microbunched electrons to characterize the coherence time of hard x-ray FEL pulses.

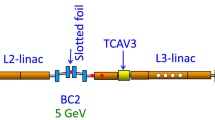
In this work, we report the first direct measurement result of the coherence time of ultra-fast hard x-ray FEL pulses through a conceptually different approach. In this method, the temporal coherence characteristics of the x-ray pulses are mapped to the cross-correlation between the microbunched electron beam and the x-ray pulse and then the corresponding coherence time can be obtained by decoding the information from the measured cross-correlation. Figure 1 depicts how this coherence time characterization method works, where the whole undulator system is considered as two parts, the first part is where the SASE FEL is generated. The coherence time of the SASE FEL pulse generated from the first part of the undulator is then to be measured in the second part, which converts the correlation information to the x-ray pulse energy. The phase shifter between these two parts is employed to manage the delay between the x-ray pulse and the microbunched electrons to produce and control the correlation.

Figure 1
figure 1

Schematic description of hard x-ray SASE FEL coherence time measurement based on cross-correlation between microbunched electrons and x-ray pulse. Hard x-ray SASE FEL is generated in the before-delay undulators, then a phase shifter is employed to generate a relative delay between the electrons and the x-ray and the final undulator converts the correlation to x-ray pulse energy. (a) Visualizing the radiation wave and the microbunched electrons at the beginning of the phase shifter. (b) Illustrating the case that the phase shifter induced delay is small. (c) Showing that when the delay is quite large, the microbunched electrons would work with x-rays in other coherence spikes.

Full size image

Principle

In the following, the essence of this method is described briefly and the details of the theoretical analysis are presented in Sec. Method. In the SASE FEL, a bunch of highly relativistic electrons enters a periodically varying magnetic field, known as undulator, in which the external magnetic field forces the electrons to wiggle transversely and emit spontaneous radiation. This process produces ultrashort bursts of x-rays at the wavelengths \({\lambda }_{r}=\frac{{\lambda }_{u}}{2{\gamma }^{2}}(1+{a}_{u}^{2})\), where λu is the undulator period, γ is the electron beam Lorentz factor and au is the RMS undulator parameter characterizing the undulator strength.

Due to the on-axis speed difference between the electrons and x-rays, the x-ray pulse propagates over the electron beam by one radiation wavelength after one undulator period. While the electron beam traveling through the undulator, the slippage between the x-rays and electrons increases continuously. This increasing slippage ls determines the cooperative-interaction range between the electrons and the x-rays, and results in coherence spike development. Hence, within the coherence spike, the x-ray and electrons would have a strong correlation18. Since these coherent spikes are all evolved from shot noise, x-rays and electrons in different coherence spikes are independent of each other. Now, it is clear that the coherence time of the FEL pulse is determined by the length of the temporal coherence spike. In spite of some coherence enhanced schemes19,20,21, the length of the coherent spike is usually much shorter than the pulse duration for hard x-ray FELs. For example, LCLS, operated in the mode of hard x-ray SASE FEL, generates x-ray pulses with tens of coherence spikes22,23,24, i.e., the coherent time is only a few hundredth of x-ray SASE FEL pulse duration.

Based on the above idea, we can trace the correlation between the microbunched electrons and the x-rays by employing a phase shifter to control the delay between them. Then, one more undulator section after the phase shifter, about one FEL gain length, is used to convert the correlation to x-ray pulse energy. It can be expected that, the pulse energy should oscillate corresponding to the delay, but with a decaying oscillation amplitude. The pulse energy oscillation comes from the phase mismatch between the microbunched electrons and x-rays in the scale of x-ray wavelength, similar to two-wave interference model; while the decaying amplitude comes from the decreasing correlation, in the scale of coherence time. This causes that after some point of delay (correlation vanishing point), the oscillation amplitude would become tiny. This characteristic of SASE FEL can be used to experimentally determine the coherence time of hard-xray pulses.

Results

We carry out experiments to measure the coherence time of hard x-ray pulses at Linac Coherent Light Source (LCLS) with the method we propose above. The experimental setup is based on the normal LCLS SASE FEL configuration25. The hard x-ray self-seeding chicane, formed by four dipoles, is employed as the phase shifter. The gas detector is used to record the x-ray pulse energy26. By distorting the electron beam orbit with quadruple magnets, we can control the after-delay FEL interaction length to maximize the interference contrast. Hysteresis-loop of magnets has also been carefully considered, so that we only monotonically increase the driving current of the magnetic chicane during the experiment and whenever we need to decrease the current, we do degauss and restart the delay scan from zero. Due to the accuracy of the driving current for the magnetic field of chicane, the step size of the delay scan is set to 0.875 attosecond and the total scan range is set to 525 attoseconds according to the coherence time estimation based on analytical studies27. To avoid the stochastic effects in the experiment as much as possible, we record 25 shots of FEL pulses for each delay and use the average value of effective shots (mostly 24 or 25 shots) to represent the pulse energy for the corresponding delay. The photon energy is tuned to be 6.92 keV, the corresponding electron beam energy is 12.48 GeV and other machine parameters are shown in Table 1.

Table 1 Key parameters for hard x-ray FEL pulse coherence time characterization.
Full size table

In our experiment, total of 15000 shots of FEL pulses are recorded. To get the effective information from the experimental data, first we synchronize the recorded data according to the time stamp and effective shots can be selected by kicking off the outliers according to the measured electron beam charge, orbit and pulse energy. Overall, 0.24% of the recorded shots are invalid and the average pulse energy of these effective shots is about 78 μJ. Raw data of the measured pulse energy and number of invalid shots for each delay are shown in Fig. 1 and Fig. 2 in the Supplementary Information, respectively. The measured pulse energy versus delay is shown in Fig. 2(a), in which the black curve is the average pulse energy over effective shots and the grey points are the pulse energy for each shot. According to Eq. (6) in Method, we employ moving variance to extract the oscillation amplitude from the recorded pulse energy and use Gaussian-like function (\(Aexp({(t-{t}_{0})}^{2}/2{\sigma }_{t}^{2})+C\)) to fit the data to obtain the value of σt, in which C is used to get rid of background noise. The blue line in Fig. 2(b) shows the decaying oscillation amplitude and the red line is the Gaussian-like fitting curve. According to the fitting results, the σt is 49.05 attoseconds and the corresponding coherence time is 174.7 attoseconds (see Method, Eq. (7)).

Figure 2
figure 2

Experimental results of hard x-ray SASE FEL coherence time measurement at LCLS: (a) Pulse energy versus delay, in which the black line is the average pulse energy for each delay and the grey points represent the single-shot pulse energy. (b) Moving variance with respect to delay, where blue points are obtained by Eq. (6) in Method and the red line is the fitting curve.

Full size image

In Fig. 2(a), the fine pulse energy oscillation we expect is blurred. To find the possible causations, we first simulate the FEL process ideally and then add hypothetical jitters (based on operation experience and physics interpretation) into the system to see whether these jitters would blur the results. We enhance the GENESIS 1.3, a well-benchmarked 3D time-dependent FEL simulation code28, to efficiently simulate the FEL process with both phase space stretch and time-delay effects included. The simulation configuration is the same as that of the experiment we mentioned above, which is the baseline of LCLS. Similar to the experiment, we scan the delay from 0 attosecond to 525 attoseconds with a step size of 0.875 attosecond. The temporal profile and bunching factor profile of the zero-delay radiation are shown in Fig. 3(a,b) respectively. Figure 3(a) shows that in the time domain, there are many isolated coherence spikes within a SASE FEL pulse. Figure 3(b) illustrates that the bunching has a similar pattern with the radiation profile. Figure 3(c) shows that if the initial shot-noise is fixed, the fine pulse energy oscillation can be clearly observed. Then, we count shot to shot initial noise fluctuation in and the average of 25 shots is considered as the pulse energy at each delay. As shown in Fig. 3(d), we can find that that if the delay is quite small the pulse energy oscillation mainly comes from the varying correlation between the microbunched electrons and the x-rays; and if the delay is sufficiently long, the pulse energy fluctuation is dominated by shot-noise and the fine pulse energy oscillation disappears.

Figure 3
figure 3

Fluctuation source analysis. (a) Time-domain description of hard x-ray SASE FEL pulse. (b) Bunching factor profile. (c) Pulse energy versus delay (ideal). (d) Pulse energy versus delay (initial shot noise fluctuation considered). (e) Pulse energy versus delay (experimental fluctuation sources considered), in which the black line is the average pulse energy and the grey points represent the pulse energy for each single-shot. (f) The moving variance obtained by Eq. (6) together with its fitting curve.

Full size image

However, besides the shot to shot initial noise fluctuation, there are a bunch of other experimental fluctuation sources, e.g., spontaneous radiation, electron beam central energy jitter and chicane’s driving current jitter. Based on our experiment result, we estimate the average (detected) spontaneous radiation energy to be about 60 μJ and assume it is proportional to the number of electrons we detected for each shot. According to previous operation experience, the relative central energy fluctuation of LCLS electron beam is about 3 × 10−4. This central energy fluctuation would be converted to delay fluctuation by the chicane. When the delay is larger than 200 attoseconds, the delay fluctuation will be the same magnitude of wavelength. Besides the electron beam central energy jitter, the chicane’s driving current jitter is another source of delay fluctuation, which is about 1.8 μA empirically. Different from electron beam central energy jitter, the chicane’s driving current jitter can directly affect the delay and this effect can be evident even when the delay is small. Although the delay fluctuation looks small, it has a strong impact on the pulse energy we measured, since the delay jitter affects the interference phase a lot. Compared with normal FEL operations, the chicane’s driving current jitter and electron beam central energy jitter are the main sources of the additional statistical variation. Then, we can try to mimic the experimental situation by adding these fluctuation sources into the ideal simulations mentioned above. The result is shown in Fig. 3(e), in which light gray points represent simulations with different noise at certain delays and the black line is the average radiation energy over different shot-noise cases. It can be found that similar to Fig. 2(a), the fine pulse energy oscillation becomes blurry. With the same data post-process approach base on Eq. (7) in Sec. Method, we can obtain a coherence time of 195.7 attoseconds and the moving variance and Gaussian fitting are shown in Fig. 3(f). Considering the stochastic nature of these fluctuation sources, we randomly add these effects for 10000 times and statistically the coherence time we can obtain is 200.3 ± 36 attoseconds. Although those fluctuation sources blur the fine pulse oscillation, the boundary of interference induced oscillation and shot-noise oscillation, which determines the coherence time, does not change much. The coherence time extracted from the experiment data is still reliable but with a statistical error at magnitude of tens of attoseconds.

Discussion

For the first time, we directly in time domain measure the coherence time of ultra-fast hard x-ray SASE FEL pulses with a conceptually new approach which we propose and describe in this paper. The method itself fills the vacancy of coherence time characterization in time domain for hard x-ray FELs. Looking forward, the pre-knowledge of coherence time of the x-ray pulse would potentially benefit experiments working on ultra-fast dynamics and structure imaging. It is worthwhile to point out that the approach introduced here is also applicable to seeded FEL, either external seeded29 or self-seeding30. In that case, it is presumed that a seeded FEL will have fully temporal coherence; yet, due to SASE components, or electron bunch imperfectness, the seeded FEL temporal coherence can be degraded31. The approach introduced in this manuscript can then be adopted to check this situation. It should be noted that the measured coherence time is an average result of thousands of FEL shots. It shows the overall longitudinal property of radiation beam based on the current FEL setup rather than a single shot. The method itself is proposed and developed based on FEL physics, which means that it can be applied to any high-gain FELs, like high repetition facilities32 and ultra-fast FEL33.

Method

This idea can be described with the well-known one-dimensional model, in which universally scaled collective variables are introduced to describe the FEL dynamics22. The normalized radiation field is defined as \(A=E/{(4\pi {m}_{e}{c}^{2}\gamma \rho {n}_{e})}^{1/2}\) where E is the radiation field, me is the electron mass, c is the speed of light, ne is the electron beam density and \(\rho ={({a}_{u}{\omega }_{p}/4c{k}_{u})}^{2/3}/\gamma \) is the Pierce parameter, with \({\omega }_{p}={(4\pi {e}^{2}{n}_{e}/{m}_{e})}^{1/2}\), the plasma frequency and ku = 2π∕λu, the undulator wave number. The bunching factor can be defined as \(B=\frac{1}{{N}_{\lambda }}{\sum }_{j=1}^{{N}_{\lambda }}{e}^{-i{\theta }_{j}}\), where θj = (ku + kr)z − ckrtj is the ponderomotive phase, kr is the radiation wave number, z is the coordinate along the undulator axis, tj is time and Nλ is the number of electrons within one radiation wavelength λr. As for the dynamics before the phase shifter, it is a typical high-gain SASE FEL process. Since we mainly care about the phase relation between the radiation and the microbunching in the time domain, the steady state model in the following is good enough to describe the FEL dynamics,

$$\begin{array}{ccc}\frac{\partial A(\bar{z},t)}{\partial \bar{z}} & = & B(\bar{z},t)\\ \frac{{\partial }^{2}B(\bar{z},t)}{\partial {\bar{z}}^{2}} & = & iA(\bar{z},t)\end{array}$$
(1)

where the normalized coordinate variables is introduced, \(\bar{z}=z/{l}_{g}\), with lg = λu/4πρ, the gain length. Since the SASE FEL starts from shot noise, only the noisy bunching factor is considered as the initial condition, which means only B(0, t) ≠ 0.

For the dynamics in the phase shifter, we only consider the delay effect rather than the phase space stretch induced by the R56 of the phase shifter, which is quite small compared to the radiation wavelength due to small electron beam energy modulation amplitude. If we denote the radiation field and bunching factor at the end of the undulator, also the phase shifter entrance, as \({A}_{s}({\bar{z}}_{p},t)\) and \({B}_{s}({\bar{z}}_{p},t)\), where \({\bar{z}}_{p}\) is the position of phase shifter; the radiation field and bunching factor at the end of the phase shifter would be \({A}_{s}({\bar{z}}_{p},t)\) and \({B}_{s}({\bar{z}}_{p},t+\Delta t)\) respectively, where Δt is the delay introduced by the phase shifter. Here, we suppose the phase shifter length is negligible. After the phase shifter, we use a short radiator to convert the correlation between the microbunched electron beam and the x-ray to pulse energy. We can regard the process in the after-delay part as coherent emission, since the radiator length is set to be around one gain length only to maximize the interference contrast. The derivation for this choice is given below in Sec. Method. During the coherent emission, the electron beam bunching factor can be regarded as a constant and the radiation field keeps increasing. Namely, only the first equation in Eq. (1) is valid with the bunching term as a constant. In this way, we get the radiation field \({A}_{c}(\bar{z},t)\) at the end of the radiator as,

$${A}_{c}(\bar{z},t)={A}_{s}({\bar{z}}_{p},t)+{B}_{s}({\bar{z}}_{p},t+\Delta t)(\bar{z}-{\bar{z}}_{p})$$
(2)

It is a good approximation that the SASE radiation field at entrance of the phase shifter is a supposition of a bunch of Gaussian-envelop plane waves with different random relative phases, intensity centers, and similar variances which can be expressed as

$${A}_{s}({\bar{z}}_{p},t)={\sum }_{j=1}^{n}{A}_{j}{e}^{-\frac{{(t-{t}_{j})}^{2}}{4{\sigma }_{t}^{2}}}{e}^{i(\omega t+{\phi }_{j})}$$
(3)

Therefore, the \({A}_{c}(\bar{z},t)\) can be further expressed as,

$$\begin{array}{ccc}{A}_{c}(\bar{z},t) & = & {\sum }_{j=1}^{n}{A}_{j}[{e}^{-\frac{{(t-{t}_{j})}^{2}}{4{\sigma }_{t}^{2}}}{e}^{i(\omega t+{\phi }_{j})}+\\ & & {e}^{-\frac{{(t+\Delta t-{t}_{j})}^{2}}{4{\sigma }_{t}^{2}}}{e}^{i[\omega (t+\Delta t)+{\phi }_{j}+\frac{\pi }{6}]}(\bar{z}-{\bar{z}}_{p})]\end{array}$$
(4)

Equation (4) shows that basically the radiation field is formed by n modes. Each mode contains two Gaussian-envelop waves, in which the first one comes from the SASE laser pulse generated in the first undulator system and the second one comes from the microbunched electron beam coherent emission. Also, we can see that the after-delay radiator length \(\bar{z}-{\bar{z}}_{p}\) determines the second wave amplitude, so that to maximize the contrast, we should set the \(\bar{z}-{\bar{z}}_{p}=1\), which means the after-delay radiator length should be one gain length. Then, the x-ray pulse energy can be expressed as,

$$\begin{array}{ccl}W & = & \int | {A}_{c}(\bar{z},t){| }^{2}dt\\ & = & 2\sqrt{2\pi }{\sigma }_{t}{\sum }_{j=1}^{n}{A}_{j}^{2}\left[1+{e}^{-\frac{\Delta {t}^{2}}{8{\sigma }_{t}^{2}}}cos\left({\omega }_{r}\Delta t+\frac{\pi }{6}\right)\right]\end{array}$$
(5)

in which quite a lot of terms counteract each other due to the sum of independent random phases. It is clear that, the x-ray pulse energy is a combination of pulse energy generated in the before-delay part, the microbunched electron beam coherent emission and their interference. The pulse energy would oscillate with a frequency of ωr = 2πc∕λ and the oscillation amplitude is a Gaussian function with \(4{\sigma }_{t}^{2}\) as its variance. Here, we can regard the exponential term as a slowly varying amplitude of the oscillation. To extract the information of the coherence time, we calculate the variance of the pulse energy which can be obtained by,

$$\begin{array}{ccc}\bar{{(W-\bar{W})}^{2}} & = & \frac{\omega }{2m\pi }{\int }_{{t}_{0}}^{{t}_{0}+\frac{2m\pi }{\omega }}{(W-\bar{W})}^{2}dt\\ & = & 4\pi {\sigma }_{t}^{2}{({\sum }_{j=1}^{n}{A}_{j}^{2})}^{2}{e}^{-\frac{\Delta {t}^{2}}{4{\sigma }_{t}^{2}}}\end{array}$$
(6)

where m is a small integer. Hence, by calculating the variance of the pulse energy in several wavelengths, we can obtain the value of σt by Gaussian fitting. According to the definition of coherence time by first-order time correlation function,

$$\begin{array}{ccc}{\tau }_{c} & = & {\int }_{-\infty }^{\infty }| \frac{ < {A}_{c}(t){A}_{c}^{* }(t+\tau ) > }{\sqrt{ < | {A}_{c}(t){| }^{2} > < | {A}_{c}(t+\tau ){| }^{2} > }}{| }^{2}d\tau \\ & = & \sqrt{4\pi }{\sigma }_{t}\end{array}$$
(7)

the coherence time of the x-ray pulse can be resolved.