Abstract
In superconductors, a topological configuration of the superconducting order parameter called a superconducting vortex carries magnetization. Such a magnetic topological object behaves like a minute particle generating a magnetic flux. Since the flux is localized with a nanometer scale, the vortex provides a nano-scale probe for local magnetic fields. Here we show that information of magnetic stripes in insulators can be read out by using vortices in an adjacent superconductor film as a probe. The orientation and width of magnetic micro stripes are both transcribed into resistance change of the superconductor through the modulation of vortex mobility affected by local magnetization. By changing the direction of external magnetic fields, zero-field resistance changes continuously according to the stripe orientation, and its modulation magnitude reaches up to 100%. The width of the stripes can also be estimated from the oscillatory magnetoresistance. Our results demonstrate a new possibility for non-volatile analog memory devices based on topological objects.
Similar content being viewed by others
Introduction
While digital computing devices have dominated electronics and information technology for several decades, analog memory devices may sow the seeds of neuromorphic computing technology. Magnetic structures in antiferromagnetic materials have attracted great attention for potential application to analog memories. Recently, a machine learning system was found to be boosted by using an analog memory effect in antiferromagnet/ferromagnet bilayer devices1. By controling internal magnetic structures of the antiferromagnetic layer continuously, they achieved memristive operation of the devices. In the antiferromagnet, the complicated magnetic structures exhibit almost zero net magnetization, which makes them robust against external magnetic disturbance and thus suitable for information storage. However, manipulating and reading magnetic information in antiferromagnets is still an unestablished job, since the spacial scale of such magnetic structures is as small as atomic scale.
In ferro- and ferri-magnetic films with perpendicular magnetic anisotropy, stripe magnetic domain structures reminiscent of antiferromagnets often appear at zero field in a nano- to micrometer-scale, where neighboring domains are arranged antiparallel along the out-of-plane direction. The stripe structures are stabilized via the competition between shape magnetic anisotropy and perpendicular magnetocrystalline anisotropy2, when the thickness of magnetic films exceeds a critical thickness3. It is known that the orientation of the stripes can be set along an external magnetic field direction to reduce the total anisotropy energy when an in-plane magnetic field greater than the saturation field is applied and then it is withdrawn; the stripe patterns are reconfigurable2. The orientation of the stripes can carry information, being a candidate for a principle of analog memories owing to its nonvolatility and robustness against magnetic fluctuations. However, no method for electrical readout of information from magnetic stripes has been found yet.
How can we detect the magnetic stripe information electrically in insulating magnets? Insulator magnets exhibit very week dissipation of magnetic dynamics, advantageous to memories and record medium. In this study, we show a mechanism for electric detection of magnetic-stripe information by using topological objects, superconducting vortices in superconductor/ferrimagnetic-insulator bilayers.
A superconducting vortex refers to a quantized magnetic flux in type-II superconductors. In superconducting films put on a magnet, stray magnetic fields created from the magnet give rise to vortices in the superconducting layer4,5,6,7 and affects the dynamics of vortices. Since the size of the vortex core is less than a micrometer, the magnetostatic interaction of the vortices8 allows us to probe micro-size magnetic structures in the magnet. Furthermore, electric detection of the internal magnetic structure in the magnet is possible by measuring resistance caused by vortex motion9 in the superconductor film; by applying a bias current to the superconducting layer, the current induces vortex motion along the direction perpendicular to the current, generating voltage parallel to the current via the vortex-Josephson effect, and thus finite resistance is produced: the vortex flow resistance9. The flow resistance is proportional to the velocity of the vortex; therefore it provides an electrical method to evaluate the mobility of vortices. When the direction of the vortex motion is perpendicular to the magnetic-stripe direction, magnetic potential barrier at the domain boundaries in the magnet lowers the mobility of the vortices in the superconductor film, giving rise to anisotropy in the vortex flow resistance, illustrated in Fig. 1a–f. By using the anisotropic transport of vortices, information of magnetic stripes can be detected, as demonstrated below.
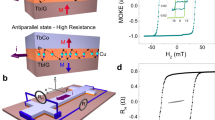
Experimental concept. (a) Consider a superconductor (SC)/ferrimagnetic insulator (FI) bilayer sample. By applying an in-plane external magnetic field, H, parallel to the y-axis and larger than the magnetization saturation field of the ferrimagnetic insulator (FI), the magnetization of FI (YIG) aligns in the same direction as the field, and magnetic domains disappear. (b) By withdrawing H from (a), perpendicularly magnetized stripes along the initially applied field direction appear in the FI layer. (c) A close-up view of (b). Superconducting vortices are created above the stripes which illustrated as confining potential for vortices. Lorentz force, F, acting on the vortices is perpendicular to the bias current. (d–f) Stripe and vortex configurations when H is applied parallel to the x-axis. (g) Measurement setup of the present study. The sample is a YIG/NbN bilayer film. An in-plane magnetic field, H, is applied at a relative angle, α, to the current direction. (h) Temperature (T) dependence of ρ for the YIG/NbN sample at H = 0. The thermodynamic superconducting transition temperature and the zero resistance temperature are denoted as Tc, and Tc0, respectively. The inset shows the T dependence of ρ up to 300 K.
Results
Figure 1 schematically illustrates the samples used in the present study and our experimental concepts. The samples are bilayer films comprising a single-crystaline (111) ferrimagnetic insulator Y3Fe5O12 (YIG) layer and a type-II superconductor NbN layer, fabricated on Gd3Ga5O12 (111) substrates (see Methods). Resistivity, ρ, of the NbN layer is measured by a 4-wire sensing method (see Fig. 1g). Temperature dependence of ρ under zero magnetic field H = 0 is shown in Fig. 1h. As the temperature T decreases from 300 K, ρ slightly increases and then exhibits superconducting transition at Tc = 11 K. ρ sharply drops at Tc and becomes lower than the measurement limit below Tc0 = 9.85 K.
In Fig. 2a,b, we show the magnetization M as a function of the in-plane H for \(H\Vert \hat{y}\) (along the long axis of the sample, see Fig. 1g) and \(H\Vert \hat{x}\) (along the short axis) at 9.9 K, together with magneto-optical images of the YIG layer. The magnetization is saturated above around Hs = 100 Oe. At H > Hs, no stripe patterns are recognized in the magneto-optical images (see Fig. 2a,b). In contrast, when H is decreased to zero, stripe patterns parallel to the initial H direction are clearly seen in the magneto-optical images for the YIG sample. The result shows that an external magnetic field can control the orientation of magnetic stripes.
Detection of magnetic stripes via magnetoresistance (MR). (a,b) Magnetic-field dependence of magnetization of the YIG/NbN sample at T = 9.9 K for α = 0 and α = 90° (for the definition of α, see Fig. 1g). We also show the magneto-optic images of the YIG sample at H > Hs and at H = 0. Magnetic stripes are observed at H = 0. (c,d) MR measured at 9.9 K, with the inplane H applied along the α = 0 and α = 90° directions. The arrows in (a–d) denote the field sweep directions. (e) The zero-field ρ obtained from the MR measurements with different α (ρH=0(α)) values at 9.9 K. The value of ρH=0(α) is normalized by ρH=0(α = 90°).
Figure 2c,d show magnetic field dependence of the resistivity ρ at T = 9.9 K, slightly higher than Tc0, at which vortices are set to move under a bias current10 (see Supplementary Fig. S1), at α = 0 and α = 90°. Here, α is defined as the angle between H and the y-axis, as shown in Fig. 1g. Importantly, ρ exhibits remarkable α dependence; as highlighted by triangles in Fig. 2c,d, the zero-H resistivity ρ(H = 0) of the NbN layer shows different values between α = 0 and α = 90°. The value of ρα=0(H = 0) is much less than that of ρα=90°(H = 0), in spite of the fact that the temperature and the bias current are same for both setups. As H decreases from high fields to zero, stripe domains are created around H = 0 in the YIG layer in response to the initial magnetic-field directions, as shown in Fig. 2a,b. Then, vortices created in the NbN layer by the stray field from the stripe domains in the YIG layer cause anisotroic vortex flow resistance in the NbN layer. The greater resistivity in the configuration where the direction of the current is perpendicular to that of the magnetic stripes is consistent with the aforementioned stronger potential barrier effect for vortices at domain boundaries. The dependence of ρ on α remains even after we insert an insulating 10 nm SiO2 film between the YIG and NbN (see Supplementary Fig. S3).
The α dependence of ρα(H = 0), obtained from the magnetoresistance (MR) measurements, at 9.9 K is shown in Fig. 2e. When the H direction α is increased from zero, ρα(H = 0) shows a maximum at α = 90° and then decreases to show a minimum at α = 180°. By further increasing α, ρα(H = 0) again shows a maximum at 270° and a minimum at 360°. The 180° periodicity can be attributed to the stripe symmetry of the magnetic stripes in the YIG. It is notable that the resistance ratio ρα(H = 0)/ρα=90°(H = 0) changes from 50% to 100% upon changing α, which is much greater than the magnitude of the conventional anisotropic magnetoresistance (AMR) in magnets. The result shows that the orientation of magnetic stripes can be detected electrically using vortex dynamics in the vicinity of Tc0, in which vortices are set to move. In Fig. 3a–e, we show MR at various T and α values. We observe no α dependence in the normal state of NbN (T = 15 K) and the zero resistivity state (T = 9.5 K). We also notice that, by increasing T, the zero field anisotropy [ρH=0(α = 90°) − ρH=0(α = 0)]/ρH=0(α = 90°) decreases. The temperature dependence of the anisotropic transport can be understood by the competition between the pinning force, the driving force and the thermal fluctuation force11. However, it requires more detailed measurements to evaluate the strength of pinning. Such measurements are beyond the scope of this study. One intuitive interpretation of the temperature dependence is at a higher temperature, vortices are thermally activated and the anisotropic pinning force from magnetic stripes become less dominate in the transport11,12. The systematic T and α dependence of ρα(H = 0) are shown in Supplementary Fig. S4.
Let us turn to the change of ρ with H. Figure 4a compares the MR curves measured for α = 0 and α = 90° at 9.95 K, where H is normalized by Hs. At a high H range (|H| > Hs = 100 Oe for α = 0) where magnetic stripes are absent, ρ monotonically increases with increasing H both for α = 0 and α = 90°. This trivial H dependence is due to the suppression of superconductivity due to the strong magnetic fields. In the H range where magnetic stripes are present (|H| < Hs), we found that ρα=90°(H) is greater than ρα=0(H), indicating that the magnetic stripes affect the vortex transport properties even in the presence of an external magnetic field. ρ in both setups reaches a minimum around Hs, where magnetic stripes disappear and the YIG layer becomes a single domain magnetic state.
Comparison of magnetoresistance and calculation. (a) Magnetoresistance (MR) measured at 9.95 K with H applied in the α = 0 and α = 90° directions. H is normalized by the saturation field Hs of the YIG layer for each α. The inset shows an MFM image at the same T for the YIG sample with H = 0. (b) A schematic illustration of the vortex matching effect. S is the cross sectional area facing H. (c) Calculated results of the magnetization process in the YIG and the magnitude of the perpendicular stray field |Hzstray| of the YIG sample. (d) Calculated MFM images at different magnetic fields.
In the range of −Hs < H < Hs, ρα=0(H) surprisingly shows oscillatory behavior: dips (local minima) at H = |0.35Hs| appear, as highlighted by the red triangles in Fig. 4a. The oscillation can be explained by a vortex matching effect in periodic pinning potential; when the period of the vortex lattice is commensurate with the period of pinning potential, the vortex motion is slowed down, resulting in electric resistance decrease13,14,15,16, (see Fig. 4b). For the α = 90° case, in contrast, ρ monotonically decreases as H increases towards Hs, where several small structures are observed. The matching effect is not remarkable in ρα=90°(H) because the driving force is parallel to the pinning channel.
A numerical calculation also supports the above scenario. We carried out numerical calculations on the magnetization process of the YIG layer under in-plane magnetic fields to estimate the H dependence of the z component of the stray field (see Method for detials). As shown in Fig. 4c, the calculated magnetization curve of the YIG layer reproduces the M-H curves experimentally observed in our YIG/NbN sample (see Fig. 2a,b); a hysteresis loop at very low fields and a sudden jump of M around H = Hs/2 are clearly reproduced in our calculations. Magnetic stripes are also reproduced: based on results from the micromagnetic simulation, we calculated MFM images at different magnetic fields. The results are shown in Fig. 4d. Note that the external field can manipulate the direction of magnetic stripes. The width of magnetic stripes is about 600 nm, slightly narrower than the actual value(~1 μm). This mismatch between simulation and experiment may come from the different thickness-to-length ratios between the model and the real sample. This may also cause a tiny difference in Hs between calculations and experiments, but it does not affect the conclusion of our discussion.
The calculated averaged magnitude of the perpendicular stray field (|Hzstray|) at 20 nm above the YIG surface as a function of H is shown in Fig. 4c. The calculated stray fields for both α = 90° and 0 decrease monotonically with |H|. No significant difference appears between α = 90° and 0. The calculation result confirms that the origin of the anisotropic resistivity dose not lie in the stray fields but in the anisotropic mobilities of vortices. The vortex matching effect appears to take place when the period of the vortex lattice matches the width of magnetic stripes4,16. From the calculated stray field, the |Hzstray| value at the matching condition is estimated to be H = 80 Oe. In previous studies4,13,14,15,16, the matching condition was estimated as Φ0/S, where Φ0 is the magnetic flux quantum and S is the cross sectional area facing H. In the present study, S = d2 (where d stands for the domain width. See Fig. 4b) and the matching magnetic field H is μ0H = Φ0/d2. We thereby estimated the width of magnetic stripes as d = 510 nm. This magnitude almost agrees with the width (~1 μm, see the inset to Fig. 4a) measured by magnetic force microscopy (MFM) at 10 K.
Harnessing the vortex anisotropic transports, we demonstrated writing and reading operation of magnetic stripes, as shown in Fig. 5. The measurement sequence is depicted in Fig. 5a. First, a weak in-plane magnetic field H = 200 Oe (>Hs) with an in-plane angle, α, is applied to the sample, followed by withdrawing the field to create stripes in the YIG layer at room temperature. This is the writing process. Then we decrease the temperature down to 10 K and measure the resistance of the NbN layer at zero field; the orientation of magnetic stripes does not change by cooling because of the nonvolatile nature of the stripes. This sequence is repeated several times at different α values to check the reproducibility of the device operation. Figure 5b shows results of three runs. In each run, we performed the writing-reading operation at α = 0, 40°, 50°, 60°, 70°, and 90°. For all the α values, the device exhibits a good reproducibility for three runs of writing and reading analog information. The magnitude of the resistance change at α = 0 and α = 90° is as large as 40%, which can differentiate the direction of magnetic stripes reliably. The present data demonstrates that the orientation of magnetic stripes can be distinguished in terms of the vortex transport with good reproducibility.
Writing and reading of magnetic stripes. (a) Procedures for the writing and reading. First, an in-plane magnetic field at an angle α to the y-axis is applied and then it is withdrawn. This procedure writes stripes with the angle α in the YIG. Then, we drop the temperature down to 10 K and measure the resistance of the NbN layer. (b) Results of three runs of writing and reading. α indicates the stripe directions. The error bars represent the standard deviation of measurements. Dotted lines are guides for the eye.
Discussion
We have demonstrated the electric readout of magnetic stripes in an insulator YIG using the vortex dynamics in superconductors. The stray field from magnetic stripes in YIG introduces superconducting vortices in an adjacent NbN layer, and the orientation and width of magnetic stripes were detected in terms of vortex flow resistance. Significant anisotropy (50–100%) in the vortex flow resistance was observed, which enables the efficient electric detection of orientation of magnetic stripes. Repetitive operation of the writing and reading processe has been confirmed to show the validity of our concept.
Anisotropic transport phenomenon in superconductors induced by fixed nanofabricated artificial grooves11, magnetic lines12, or so-called domain wall superocnductivity was reported in ferromagnet/superconductor hybrids17,18,19. In the nanostructured grooves and magnetic lines, they act as fixed guidance of vortices, different from our study that demonstrates writing and reading operations from rewritable and tunable magnetic stripes in insulator films. In the domain wall superconductivity, the stray field is higher than the upper critical field (Hc2) of the superconducting layer; the superconductivity remains only at the region above domain walls, since the stray field is smaller than that at the interior of the stripe regions. The localization of superconducting order parameter above domain walls was studied theoretically by Aladyshkin et al.20 and observed experimentally later21,22,23.
The YIG layer exhibits smaller remnant in-plane magnetization (~0.1 Ms) and perpendicular magnetic anisotropy. This ensures significant amount of out-of-plane local magnetization at zero field. Therefore the spontaneous nucleation of vortices6,7 in the NbN layer is realized, and it enables us to readout the analog information via zero-field resistivity. From the magnetic field-temperature diagram (see Supplemental Fig. S1), we obtained \(-{\mu }_{0}\frac{d{H}_{{\rm{c2}}}}{dT}{|}_{{T}_{{\rm{c}}}}=3.91\,{\rm{T}}/{\rm{K}}\), which yields to μ0Hc2(T = 0) ≈ 29.7 T and a coherence length ξ(T = 0) ≈ 3.3 nm24. In the dirty limit, we estimate the penetration length as λ(T = 0) ≈ 436 nm25. The corresponding values of μ0Hc2, ξ and λ at 9.95 K are respectively 4.6 T, 10.5 nm and 723 nm. Using the criterion from Iavarone etal.7, vortices will spontaneous nuclear once the perpendicular component of the magnetization is larger than 5.6 A/m, which is much smaller than the simulation amount (~10000 A/m) at zero field.
Furthermore, a stray field from our YIG layer is so small that it does not exceed Hc2 of the NbN layer; the transport anisotropy in the present study is due mainly to different vortex mobilities in different stripe directions. This allows us to use magnetic materials with less magnetization and anisotropy than the previous works18,26, enabling us to observe the vortex matching effect in the MR curve. The interaction between superconducting vortex and magnetic layer were reported in many aspects, such as the spontaneous nucleation of vortices6,7, the pinning of magnetic domains by superconducting vortex27, the guided vortex motion detected by magneto-optical imaging28 and transport measurements26. However, this work first demonstrates the magnet/superconductor hybrids can serve as nonvolatile analog storage elements. We point out the same mechanism may apply to other topological objects. For example, topological objects in magnets, known as skyrmions, also couple with currents and stray fields from magnetic stripes and can be used to readout stripe information under room temperature.
Methods
Sample fabrication
An epitaxial Y3Fe5O12 (111) film of the thickness 6-μm was grown on a Gd3Ga5O12 (111) 0.5-mm-thick substrate by the liquid phase epitaxy29. The sample was cut into small pieces with 1 × 3 mm2 rectangular surface area ((Lx, Ly, Lz) = (1 mm, 3 mm, 0.5 mm), see Fig. 1g). Then, NbN films with the thickness of 20 nm were sputtered at room temperature on the YIG films. For the NbN sputtering, a Nb target was sputtered in a N2-Ar mixture gas30. The YIG(111) film exhibits out-of-plane magnetic anisotropy and magnetic stripe patterns below the magnetization saturation field.
Resistivity and magnetization measurement
Resistivity (ρ) of the YIG/NbN samples was measured by a 4-wire sensing method in a physical property measurement system (PPMS; Quantum Design, Inc.). The sample was fixed on a PPMS rotator option chip with GE varnish and attached to a rotator rod. The longitudinal voltage was measured with a nanovoltmeter (2182A; Keithley, Inc.) when the bias current with the density ~108 A/m2 was applied to the sample with an a.c. current source (6221; Keithley, Inc.). The delta mode method was used in the ρ measurements to reduce noise levels. The MR was measured by sweeping magnetic fields along a direction at an angle (α) to the y-axis. Magnetization measurements were also performed in PPMS by using a vibrating sample magnetometer (VSM) option. Domain structures in a bare YIG film were observed by polarized light microscopy at room temperature and also by magnetic force microscopy (MFM) at T = 10 K.
Micromagnetic calculation
The micromagnetic calculation was performed using OOMMF31, based on the Landau-Lifshitz-Gilbert equation:
where γ, m and α are the gyromagnetic ratio, unit vector of the magnetization, and the Gilbert damping coefficient, respectively. The effective field Heff includes the external field, the exchange field, the demagnetization field, and the cubic anisotropy field. The sample size used in the simulation along the x, y, z directions are 12 μm, 24 μm and 2 μm, respectively, and the sample was divided into unit cells of 100 × 100 × 100 nm3.
Data availability
The data used to support the findings of this study are available from the corresponding author upon request.
References
Borders, W. A. et al. Analogue spin–orbit torque device for artificial-neural-network-based associative memory operation. Applied Physics Express 10, 013007 (2017).
Hubert, A. & Schäfer, R. Magnetic domains: the analysis of magnetic microstructures (Springer Science & Business Media, 2008).
Ben Youssef, J., Vukadinovic, N., Billet, D. & Labrune, M. Thickness-dependent magnetic excitations in Permalloy films with nonuniform magnetization. Physical Review B 69, 2474 (2004).
Di Giorgio, C. et al. Observation of superconducting vortex clusters in S/F hybrids. Scientific Reports 6, 622 (2016).
Karapetrov, G. et al. Transverse instabilities of multiple vortex chains in magnetically coupled NbSe2/permalloy superconductor/ferromagnet bilayers. Physical Review B 80, 180506 (2009).
Bobba, F. et al. Vortex-antivortex coexistence in Nb-based superconductor/ferromagnet heterostructures. Physical Review B 89, 214502 (2014).
Iavarone, M. et al. Imaging the spontaneous formation of vortex-antivortex pairs in planar superconductor/ferromagnet hybrid structures. Physical Review B 84, 024506 (2011).
Aladyshkin, A. Y., Silhanek, A. V., Gillijns, W. & Moshchalkov, V. V. Nucleation of superconductivity and vortex matter in superconductor–ferromagnet hybrids. Superconductor Science and Technology 22, 053001 (2009).
Tinkham, M. Introduction to superconductivity (Courier Corporation, 1996).
Lustikova, J. et al. Vortex rectenna powered by environmental fluctuations. Nature Communications 9, 4922 (2018).
Soroka, O. K., Shklovskij, V. A. & Huth, M. Guiding of vortices under competing isotropic and anisotropic pinning conditions: Theory and experiment. Physical Review B 76, 014504 (2007).
Dobrovolskiy, O. V., Huth, M. & Shklovskij, V. A. Anisotropic magnetoresistive response in thin Nb films decorated by an array of Co stripes. Superconductor Science and Technology 23, 125014 (2010).
Harada, K. et al. Direct Observation of Vortex Dynamics in Superconducting Films with Regular Arrays of Defects. Science 274, 1167–1170 (1996).
Martn, J. I., Vélez, M., Nogués, J. & Schuller, I. K. Flux Pinning in a Superconductor by an Array of Submicrometer Magnetic Dots. Physical Review Letters 79, 1929–1932 (1997).
Thakur, A. D. et al. Vortex matching effect in engineered thin films of NbN. Applied Physics Letters 94, 262501 (2009).
Belkin, A., Novosad, V., Iavarone, M., Pearson, J. & Karapetrov, G. Superconductor/ferromagnet bilayers: Influence of magnetic domain structure on vortex dynamics. Physical Review B 77, 180506 (2008).
Aladyshkin, A. Y., Fritzsche, J. & Moshchalkov, V. V. Planar superconductor/ferromagnet hybrids: Anisotropy of resistivity induced by magnetic templates. Applied Physics Letters 94, 222503 (2009).
Belkin, A. et al. Tunable transport in magnetically coupled MoGe/Permalloy hybrids. Applied Physics Letters 93, 072510 (2008).
Aladyshkin, A. Y. et al. Crossover between different regimes of inhomogeneous superconductivity in planar superconductor-ferromagnet hybrids. Physical Review B 84, 094523 (2011).
Aladyshkin, A. Y. et al. Domain-wall superconductivity in hybrid superconductor-ferromagnet structures. Physical Review B 68, 184508 (2003).
Yang, Z., Lange, M., Volodin, A., Szymczak, R. & Moshchalkov, V. V. Domain-wall superconductivity in superconductor-ferromagnet hybrids. Nature materials 3, 793–798 (2004).
Buzdin, A. Mixing superconductivity and magnetism. Nature materials 3, 751–752 (2004).
Iavarone, M. et al. Visualizing domain wall and reverse domain superconductivity. Nature Communications 5, 4766 (2014).
Werthamer, N. R., Helfand, E. & Hohenberg, P. C. Temperature and Purity Dependence of the Superconducting Critical Field, Hc2. III. Electron Spin and Spin-Orbit Effects. Physical Review 147, 295–302 (1966).
Kes, P. H. & Tsuei, C. C. Two-dimensional collective flux pinning, defects, and structural relaxation in amorphous superconducting films. Physical Review B (Condensed Matter) 28, 5126–5139 (1983).
Vlasko-Vlasov, V. K. et al. Soft magnetic lithography and giant magnetoresistance in superconducting/ferromagnetic hybrids. Physical Review B 78, 214511 (2008).
Fritzsche, J., Kramer, R. B. G. & Moshchalkov, V. V. Visualization of the vortex-mediated pinning of ferromagnetic domains in superconductor-ferromagnet hybrids. Physical Review B 79, 132501 (2009).
Vlasko-Vlasov, V. et al. Guiding superconducting vortices with magnetic domain walls. Physical Review B 77, 134518 (2008).
Qiu, Z. et al. Spin mixing conductance at a well-controlled platinum/yttrium iron garnet interface. Applied Physics Letters 103, 092404 (2013).
Umeda, M. et al. Spin-current coherence peak in superconductor/magnet junctions. Applied Physics Letters 112, 232601 (2018).
Donahue, M. J. & Porter, D. G. OOMMF User’s Guide, Version 1.0 (Interagency Report NISTIR 6376, National Institute of Standards and Technology, Gaithersburg, MD, 1999).
Acknowledgements
We thank J. Lustikova, Y. Hashimoto, D. Hou, Z. Qiu and J. Ohe for valuable discussions. We also thank K. Nagase for experimental help. This research was supported by JST ERATO Spin Quantum Rectification Project (JPMJER1402), JSPS KAKENHI (18H04215, 18H04311, 19H02424, 18J21304, 19J13544) and MEXT (Innovative Area Nano Spin Conversion Science (No. 26103005)). This work was also supported by the National Natural Science Foundation of China (Grant No. 11874098), LiaoNing Revitalization Talents Program (XLYC1807156), and the Fundamental Research Funds for the Central Universities (DUT17RC(3)073). Y.C. and M.U. are supported by GP-Spin at Tohoku University and the Japan Society for the Promotion of Science through a research fellowship for young scientists.
Author information
Authors and Affiliations
Contributions
Y.C. conceived and designed the experiments in discussion with Y.S. and E.S. Y.C. performed the experiments and analyzed the experimental data. Y.C., T.N. and M.U. fabricated the NbN films. Z.Q. fabricated the YIG films. Y.C. conducted micromagnetic simulation. E.S. supervised the project. All authors discussed the results and commented on the manuscript, which was written by Y.C., Y.S. and E.S.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, Y., Shiomi, Y., Qiu, Z. et al. Electric readout of magnetic stripes in insulators. Sci Rep 9, 19052 (2019). https://doi.org/10.1038/s41598-019-55565-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-55565-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.