Abstract
We propose a feasible and efficient dynamic multiparty quantum private comparison protocol that is fully secure against participant attacks. In the proposed scheme, two almost-dishonest third parties generate two random keys and send them to all participants. Every participant independently encrypts their private information with the encryption keys and sends it to the third parties. The third parties can analyze the equality of all or some participants’ secrets without gaining access to the secret information. New participants can dynamically join the protocol without the need for any additional conditions in the protocol. We provide detailed correctness and security analysis of the proposed protocol. Our security analysis of the proposed protocol against both inside and outside attacks proves that attackers cannot extract any secret information.
Similar content being viewed by others
Introduction
The pioneering work of Bennett and Brassard1 laid the groundwork for the rapidly growing field of quantum cryptography and quantum communication. Subsequently, various quantum protocols have been proposed including Shor’s algorithm for factoring2,3,4, quantum teleportation5,6,7,8,9, superdense coding10,11,12,13, quantum secure direct communication14,15,16, quantum secret sharing17,18,19,20,21, quantum dialogue22,23 and quantum key agreement24,25. In 1982, the millionaires’ problem was proposed as a possible application of secure multiparty computing26, the goal is for two parties to compare their wealth and learn who is wealthier without revealing any extra data about the other’s wealth. In 2001, an efficient and fair solution to the socialist millionaires’ problem was proposed27. Furthermore, a solution for the socialist millionaires’ problem based on homomorphic encryption in a semi-honest environment was discussed28. Lo29 proved that the task of secure two-party computation is unachievable even with quantum cryptography29. Therefore, a quantum private comparison (QPC) protocol for comparing the equality of information with the help of a third party (TP) was proposed30. Furthermore, Hung et al.31 proposed a secure QPC protocol with two almost-dishonest TPs. In general, there are four common levels of TP’s trustworthiness32,33: (1) TP is fully honest. In this circumstance, the participants only send their encrypted secrets to the TP. The TP then compares the private information of the participants and announces the final result. This situation is surely ideal, but finding a fully honest TP in the real world could be challenging. (2) TP is dishonest such that all participants cannot trust the TP. This assumption is equivalent to the standard two-party QPC protocols without a TP, whose insecurity was proved by Lo29. (3) TP is semi-honest. Under this circumstance, the participants can partially trust the TP. The TP honestly executes the required processes and may eavesdrop on participants’ private information using passive attacks31. (4) TP is almost-dishonest. This situation, which is more reasonable, assumes that the participants can partially trust the TP, and the TP may perform any active attack while executing the protocol, except conspiring with dishonest participants31. In general, QPC protocols can be used for novel and existing applications, including quantum voting34,35, quantum bidding36, and quantum auctions37,38,39.
Chang et al. proposed the first multiparty quantum private comparison (MQPC) protocol for comparing the equality of secrets of any two parties among M participants40. The protocol used GHZ states as a quantum resource. Subsequently, a novel QPC protocol that included the support of a semi-honest TP and used d-dimensional entangled photons was proposed41. An MQPC protocol based on entanglement swapping of Bell states was subsequently presented42. This scheme used the one-way hash function to address information leakage issue and to encrypt secret information between the communicating parties. A pioneering M-participant QPC protocol that addressed the possibility of a dishonest TP collaborating with participants was discussed43. Furthermore, a novel MQPC protocol with a semi-honest TP that used entanglement swapping of d-level states and a unitary operation to encrypt the participants’ secrets was proposed44. Then, Hung et al.31 presented a QPC protocol consisting of two third-parties in which one is malicious and the other is almost dishonest was presented. A multi-user QPC protocol that employs both scattered preparation operation and one-way convergent transmission operation of quantum states was also proposed45, where two participants can compare their secrets with the support of the remaining participants using the polarization and spatial-mode degrees of freedom of photons to transmit information. Liu et al.46 proposed a QPC protocol in which any participant can join dynamically to participate in the comparison of M participants.
These quantum private comparison protocols still suffer from low efficiency and an inadequate level of security. Therefore, this work proposes a feasible, efficient, and secure dynamic multiparty quantum private comparison protocol (DMQPC) that uses single-photons to encode and send encrypted information. Our proposed scheme has several important features. First, dishonest participants cannot individually or jointly attack the scheme to gain any private or secret information since every participant independently encrypts and transmits secret information to two TPs without the involvement or assistance of other participants. Second, our protocol is dynamic and flexible such that multiple participants can join or leave the protocol and the two TPs can successfully compare the encrypted information of any subset of M participants. Third, the participants only generate and transmit single photons, and the two TPs generate single photons and perform single-photon measurements. Hence, the cost of the deployed quantum devices and the employed quantum operations is reduced, and the efficiency of the proposed protocol is increased. Finally, the communication cost is significantly reduced since the proposed protocol can be executed in a variable number of rounds. We describe our scheme and provide proofs and illustrative examples in the following sections. Section 2 introduces the proposed DMQPC protocol. Section 3 verifies the correctness of the proposed scheme. The security analysis is presented in Section 4. Section 5 discussed the efficiency of the scheme and comparisons to some previous protocols. We show that our scheme is more feasible, efficient, secure and flexible compared to other protocols. Section 6 introduces comparisons to some existing QPC protocols. A summary and conclusion is presented in Section 7.
The Proposed DMQPC Protocol
Here, we will discuss the DMQPC protocol for three different scenarios, namely two-party QPC with two rounds, DMQPC with two rounds and DMQPC with B-block. Before the comparison of data, there are two main processes: (1) validation check process; (2) the initial preparation and encryption process. The two processes are similar in the three scenarios. So, they will be described in detail only for two-party QPC with two rounds.
Two-party QPC with two rounds
Suppose that Alice and Bob intend to compare the equality of their secrets X and Y, respectively, with the help of two almost-dishonest TPs. The binary representation of X in F2n is (x0, x1, ..., xn−1), and the binary representation of Y in F2n is (y0, y1, ..., yn−1) where Xi, Yi ∈ {0, 1}n and n ≥ 2 is the number of secret bits. In general, a protocol with two TPs has many advantages such as: (1) improving load balance performance since we can distribute the workload to two TPs (servers) instead of only one; (2) increasing availability that ensures continuity of communication; (3) ensuring security since one TP can monitor the performance of the other one31. The idea of adopting two TPs to execute the comparison task in QPC was first suggested by Hung et al.31. In our work, the advantage of using two TPs is that one can generate two independent random keys by two different TPs. More specifically, the first third-party (TP1) computes the comparison result of the first round. The second third-party (TP2) computes the comparison result of the second-round. Both TP1 and TP2 prepare a random secret key and send it to both Alice and Bob.
Validation check process
Firstly, X and Y must have the same length. Secondly, to correctly execute the proposed QPC protocol, secret data must be checked as follows; If the length of X(Y) is odd, then Alice (Bob) must replace the last bit with two bits;
Initial Preparation and Encryption Process
TP1 and TP2 prepare two random secret keys \({{\rm{K}}}_{rand}^{TP1}\) and \({{\rm{K}}}_{rand}^{TP2}\), respectively, and send them through quantum channels to both Alice and Bob16,47. Alice and Bob compute \({K}_{rand}={{\rm{K}}}_{rand}^{TP1}\oplus {{\rm{K}}}_{rand}^{TP2}\), where \(|{K}_{rand}|=|{{\rm{K}}}_{rand}^{TP1}|=|{{\rm{K}}}_{rand}^{TP2}|=|X|=|Y|\). Then Alice and Bob split Krand into two equal parts \({K}_{rand}^{1}\) and \({K}_{rand}^{2}\), where Krand ∈ {0, 1}n and \({K}_{rand}^{1},{K}_{rand}^{2}\in {\{0,1\}}^{\frac{n}{2}}\). To reduce the communication cost, Alice also divides X into two equal parts Xpart_1 and Xpart_2. Alice then computes
The encrypted parts X1 and X2 can be represented as follows.
where X1 and X2 are the first and second parts of X encrypted with \({K}_{rand}^{1}\) and \({K}_{rand}^{2}\), respectively. Similarly, Bob computes Y1 and Y2 just as Alice does.
where Y1 and Y2 are the first and second parts of Y encrypted with \({K}_{rand}^{1}\) and \({K}_{rand}^{2}\), respectively. Also, we have X12 = X1 ⊕ X2 and Y12 = Y1 ⊕ Y2. Here, ⊕ is the exclusive-OR operation.
As shown in Table 1, Alice generates new encoded parts \({X}_{1}^{\text{'}}\) and \({X}_{12}^{\text{'}}\) from X1, X2, and X12 according to the following rule: If the bit value of X1 = X12 = 0(X1 = X12 = 1) then \(\,{X}_{1}^{\text{'}}={X}_{12}^{\text{'}}=1\,({X}_{1}^{\text{'}}={X}_{12}^{\text{'}}=0)\). Otherwise, \({X}_{1}^{\text{'}}={X}_{1}\) and \({X}_{12}^{\text{'}}={X}_{12}\), where \({X}_{1}^{\text{'}}\) and \({X}_{12}^{\text{'}}\) are updated parts of X1 and X12. The purpose of this process is to relate the secret message parts to each other so that we can reduce the communication cost. That is to say, it is possible to only compare one part of the secret messages in some situations to get the final result.
From Table 1, we can get the sequences \({X}_{1}^{\text{'}}\), X12, and \({X}_{12}^{\text{'}}\), with length \(\frac{n}{2}\):
Alice uses the XOR function to encrypt X1 with \({X}_{1}^{\text{'}}\) getting Ca1,
Similarly, Bob performs the same processes as Alice does,
Alice computes X12 = X1 ⊕ X2:
Bob also computes Y12 = Y1 ⊕ Y2:
In our protocol, we have three options to compute and announce the comparison result. The first option would be for TP1 to compute and announce (in the first and second rounds) the comparison result. The second option would be for TP2 to compute and announce the comparison result. These two options can be used when availability of at least one TP is the most important requirement. The third option would be for the two TPs to collaborate to compute and announce the final result. The steps for executing the two rounds to compare the equality of parties’ secrets are similar in the three options. The choice of which of the three options to use depends on whether the priority is availability, workload or security. The two rounds are described as follows.
The first-round
Step 1. TP1 asks Alice and Bob to prepare Ca1 = X1 ⊕ \({{\rm{X}}}_{1}^{\text{'}}\) and Cb1 = Y1 ⊕ \({{\rm{Y}}}_{1}^{\text{'}}\), respectively.
Step 2. Alice prepares a sequence of \(\frac{n}{2}\) single photons, called Sa1, corresponding to Ca1 in the Z-basis {|0〉, |1〉} or the X-basis \(\{|+\rangle =\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle ),|-\rangle =\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle )\}\).
Step 3. For the eavesdropping check, Alice randomly prepares a sequence of decoy photons la1 in one of the states {|0〉, |1〉, |+〉, |−〉}. At random positions, she inserts la1 into Sa1 producing a new sequence \({S}_{a1}^{\text{'}}\). Then, Alice transmits \({S}_{a1}^{\text{'}}\) to the TP1.
Step 4. Alice announces the random positions and the measurement bases of la1 to TP1 for performing single photon measurements. TP1 then reveals the measurement outcomes. Hence, TP1 and Alice analyze the error rate. If the rate is higher than a predetermined threshold, then they terminate the protocol and restart the process again. Otherwise, TP1 discards la1 from \({S}_{a1}^{\text{'}}\) and extracts Sa1. Then TP1 can restore Ca1, where Sa1 represents Ca1.
Step 5. Bob and TP1 perform the same Steps 2–4 as Alice and TP1 to send Cb1 to TP1.
Step 6. TP1 performs a comparison between the first part of Alice’s and Bob’s secrets by computing R1 = Ca1 ⊕ Cb1. If R1 = 0, this indicates that X and Y may be equal. In this case, they move to the next round to check whether Alice’s and Bob’s secrets are equal or not. Otherwise, X and Y are not equal, so there is no need to continue to the second-round to check the equality of the second parts.
The second-round
Step 7. TP1 informs TP2 that the first-round comparison result may be equal. Then TP2 asks Alice and Bob to prepare X12 and Y12, respectively.
Step 8. Alice and Bob perform the same processes described in Steps 2–4 to send X12 and Y12 to TP2.
Step 9. TP2 computes R2 = X12 ⊕ Y12. If R = R1 + R2 = 0 then X and Y are equal. Otherwise, X and Y are not equal. A detailed example to check the equality of X = {001100110010} and Y = {011100110010} is shown in Tables 2 and 3.
Adding new participants
One of the main features of this protocol is the ease of joining of one or more participants. Without loss of generality, suppose a new participant called Charlie want to joint the old participants (Alice and Bob). The steps for adding a new participant are described as follows.
The first-round
Step 1. Charlie asks TP1 and TP2 to join the protocol.
Step 2. TP1 asks Charlie to prepare \({{\rm{C}}}_{c1}={{\rm{Z}}}_{1}\oplus {{\rm{Z}}}_{1}^{\text{'}}\) using the same protocol as Alice and Bob to prepare Ca1 and Cb1, respectively.
Step 3. Charlie prepares a sequence of \(\frac{n}{2}\) single photons, called Sc1, corresponding to Cc1 in the Z-basis {|0〉, |1〉} or the X-basis \(\{|\,+\,\rangle =\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle ),|\,-\,\rangle =\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle )\}\).
Step 4. For eavesdropping check, Charlie randomly prepares a sequence of decoy photons lc1 in one of the states {|0〉, |1〉, |+〉, |−〉}. At random positions, he inserts lc1 into Sc1 producing a new sequence \({S}_{c1}^{\text{'}}\). Then, Charlie transmits \({S}_{c1}^{\text{'}}\) to the TP1.
Step 5. Upon receiving \({S}_{c1}^{\text{'}}\), Charlie announces the random positions and the measurement bases of lc1 to TP1 for performing single photon measurements. TP1 then reveals the measurement outcomes. Hence, TP1 and Charlie analyze the error rate. If the rate is higher than a predetermined threshold, then they terminate the protocol and restart the process again. Otherwise, TP1 discards lc1 from \({S}_{c1}^{\text{'}}\) and extracts Sc1. Then TP1 can restore Cc1.
Step 6. TP1 performs a comparison between the first part of Alice’s, Bob’s, and Charlie’s secrets by computing R1 = (Ca1 ⊕ Cb1) + (Cb1 ⊕ Cc1). If R1 = 0, this indicates that X, Y, and Z may be equal. In this case, they move to the next round to check whether Alice’s, Bob’s, and Charlie’s secrets are equal or not. Otherwise, X, Y, and Z are not equal, so there is no need to continue to the second-round to check the equality of the second parts.
The second-round
Step 7. TP1 informs TP2 that the first-round comparison result may be equal. Then TP2 asks Charlie to prepare Z12 using the same protocol as Alice and Bob to prepare X12 and Y12, respectively.
Step 8. Charlie performs the same processes described in Steps 3–4 to send Z12 to TP2.
Step 9. TP2 computes R2 = (X12 ⊕ Y12) + (Y12 ⊕ Z12). If R = R1 + R2 = 0, TP2 announces to Alice, Bob, and Charlie that X, Y, and Z are equal. Otherwise, X, Y, and Z are not equal.
Deleting old participants
Without loss of generality, suppose we have three participants Alice, Bob, and Charlie. TP1 and TP2 are allowed to delete one or more participants (e.g., Charlie) for several reasons. For example, they may want to compare just Bob’s and Alice’s private information. The detailed steps for deleting Charlie are as follows.
The first-round
Step 1. TP1 and TP2 agree to delete Charlie. TP1 then discards Cc1.
Step 2. TP1 updates the comparison process, to be only between Alice and Bob, TP1 then recomputes R1. In that case, TP1 computes and considers the result of R1 = Ca1 ⊕ Cb1 instead of R1 = (Ca1 ⊕ Cb1) + (Cb1 ⊕ Cc1). If the result of R1 = 0, this indicates that X and Y may be equal. In this case, they move to the next round to check whether Alice’s and Bob’s secrets are equal or not. Otherwise, X and Y are not equal and the final result is announced.
The second-round
Step 3. TP1 informs TP2 that the first-round comparison result of Alice’s and Bob’s secrets may be equal.Step 4. TP2 discards the encrypted information of Charlie (Z12) and only considers the private information of Alice and Bob, that is, X12 and Y12, respectively.
Step 5. TP2 computes and considers R2 = X12 ⊕ Y12 instead of R2 = (X12 ⊕ Y12) + (Y12 ⊕ Z12). If R = R1 + R2 = 0 then X and Y are equal. Otherwise, X and Y are not equal.
Multi-party QPC with two rounds
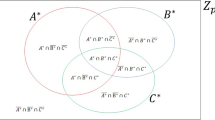
The proposed two-party QPC protocol is easy to extend to M participants (see Fig. 1). In this scenario, there are M participants Pi (i = 1, 2, ..., M), and each of them has secret information \({X}_{i}^{\ast }\) with length n. Firstly, participants check the validity of their secrets according to the validation check process. After they make sure that their secrets are valid for applying the proposed protocol, TP1 and TP2 send two random secret keys (\({{\rm{K}}}_{rand}^{TP1}\) and \({{\rm{K}}}_{rand}^{TP2}\)) with length n to all participants. Pi then perform the initial preparation and encryption process as shown in Eqs. (2–5) for producing \({X}_{i,1}^{\ast }\) and \({X}_{i,2}^{\ast }\). From Table 1, each participant gets the sequences \({X}_{i,1}^{\ast }\) and \({X}_{i,2}^{\ast }\), with length \(\frac{n}{2}\) for each sequence. Also, each participant computes Ci,1 = \({X}_{i,1}^{\ast }\) ⊕ \({X}_{i,1}^{^{\prime} }\). Now each participant has completed preparing encrypted secrets, and they are ready for checking the equality of their secrets using the QPC protocol.
The first-round
Step 1. TP1 asks each participant to prepare Ci,1.
Step 2. Pi prepares a quantum sequence containing \(\frac{n}{2}\) single photons corresponding to Ci,1 (i.e. Si,1) in the Z-basis {|0〉, |1〉} or X-basis \(\{|+=\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle ,|\,-\,\rangle =\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle )\}\).
Step 3. For the eavesdropping check, Pi randomly prepares a sequence of decoy photons li,1 in one of the states {|0〉, |1〉, |+〉, |−〉}. At random positions, Pi inserts li,1 into Si,1 producing a new sequence \({S}_{i,1}^{\text{'}}\). Then, Pi sends \({S}_{i,1}^{\text{'}}\) to the TP1.
Step 4. Upon receiving \({S}_{i,1}^{\text{'}}\), Pi announces the random positions and the measurement bases of li,1 to TP1 for performing single photon measurements. TP1 then announces the measurement outcomes. TP1 and Pi analyze the error rate. If the rate is higher than a predetermined threshold, they terminate the communication and restart the process again. Otherwise, TP1 discards li,1 from \({S}_{i,1}^{\text{'}}\) and extracts Si,1. Then the TP1 can restore Ci,1, where Si,1 represents Ci,1.
Step 5. TP1 performs a comparison of the first part of Pi’s secret, where for M = 3
For M > 3
If R1 = 0, \({X}_{1}^{\ast },\,{X}_{2}^{\ast },\,\ldots ,\,{X}_{M}^{\ast }\) may be equal. Hence, they move to the next round to compute the comparison check of Xi,12. Otherwise, \({X}_{1}^{\ast },{X}_{2}^{\ast },\ldots ,\,{X}_{M}^{\ast }\) are not equal. Then it is not necessary to execute the second-round to check the equality of Xi,12.
The second-round
Step 6. TP1 informs TP2 that the first-round comparison result may be equal. Then TP2 asks Pi to prepare Xi,12.
Step 7. Pi performs the same processes as in Steps 2–4 to send Xi,12 to TP2.
Step 8. TP2 computes the comparison check of Xi,12,
where for M = 3
for M > 3
Now, TP2 can compute R = R1 + R2 to determine whether \({X}_{1}^{\ast },{X}_{2}^{\ast },\,\ldots ,\,{X}_{M}^{\ast }\) are equal or not. If \({X}_{1}^{\ast },{X}_{2}^{\ast },\,\ldots ,\,{X}_{M}^{\ast }\) are equal. Otherwise, \({X}_{1}^{\ast },{X}_{2}^{\ast },\,\ldots ,\,{X}_{M}^{\ast }\) are not equal. Obviously, it is easy to add or remove any subset of participants to the protocol, where participants independently perform the required processes to prepare their secret for the final step of the protocol. Moreover, TP1 and TP2 can easily compare the equality of the secrets of any subset of M participants without any additional conditions.
Multi-Party QPC with B blocks
The secret data can be divided into several blocks (B), which could be useful in comparing the equality of big data. Each block contains \(\frac{n}{B}\) bits and is executed in two rounds, where \(\frac{n}{B}\) is an even number such that,
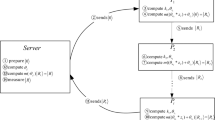
Suppose there are M participants Pi (i = 1, 2, ..., M). Each of them has secret information Xi with a length of n, and they would like to check the equality of their secrets. Firstly, all participants check the validity of their secrets according to the previously described validation check. After they make sure that their secrets are valid for applying the proposed protocol, TP1 and TP2 send two random secret keys (\({{\rm{K}}}_{rand}^{TP1}\) and \({{\rm{K}}}_{rand}^{TP2}\)) with length n to all participants. Based on the length of the secret data (n), TP1 and TP2 agree with participants on the value of B (see Fig. 2). Pi computes \({K}_{rand}={{\rm{K}}}_{rand}^{TP1}\oplus {{\rm{K}}}_{rand}^{TP2}\) and divides Krand into B blocks. Each block contains two sub-keys \({{\rm{K}}}_{rand}^{1,\,j}\) and \({{\rm{K}}}_{rand}^{2,\,j}\), where j = 1,2, …, B.
Subsequently, Pi performs the initial preparations as previously indicated in Eq. (2) and Eq. (3) for generating \({X}_{i,j}^{1}\) and \({X}_{i,j}^{2}\), where i = 1, 2, …, M. At this point, using Table 1, participants can easily prepare their encrypted secret information producing Ci,j and \({X}_{12}^{i,j}\), and are ready to check the equality of their secrets using the following steps.
The first-round
Step 1. TP1 asks each participant to prepare Ci,j.
Step 2. Pi prepares a sequence of \(\frac{n}{2B}\) single photons for each block, called Si,j, corresponding to Ci,j, in the Z-basis {|0,〉 |1〉} or X-basis \(\{|\,+\,\rangle =\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle ),|\,-\,\rangle =\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle )\}\).
Step 3. To prevent eavesdropping, Pi randomly prepares a sequence of decoy photons li,j in one of the states {|0〉, |1〉, |+〉, |−〉}. At random positions, Pi inserts li,j into Si,j producing a new sequence \({S}_{i,1}^{\text{'}}\). Pi then sends \({S}_{i,1}^{\text{'}}({S}_{i,2}^{\text{'}},\,\ldots ,\,{S}_{i,B}^{\text{'}})\) to TP1.
Step 4. Upon receiving \({S}_{i,j}^{\text{'}}\), Pi announces the random positions and the measurement bases of li,j to TP1 for performing single photon measurements. TP1 then announces the measurement outcomes. TP1 and Pi analyze the error rate. For any error rate above a predetermined threshold, they cancel the communication and restart all over again. Otherwise, TP1 discards li,j from \({S}_{i,j}^{\text{'}}\) and extracts Si,j. TP1 then can construct Ci,j, where Si,j represents Ci,j.
Step 5. TP1 computes the comparison check of Ci,j, where for M = 3
For M > 3
If \({R}_{1}^{1}=0\,({R}_{1}^{2}=0,\ldots ,{R}_{1}^{B}=0)\), X1, X2, …, XM may be equal, where \({R}_{1}^{B}\)is the comparison result of the first round of block number B for all participants. Hence, they move to the next round to compute the comparison check of \({X}_{12}^{i,1}\) \({X}_{12}^{i,2},\,\ldots ,\,{X}_{12}^{i,B}\). Otherwise, their secrets are not equal.
The second-round
Step 6. TP1 informs TP2 that the first-round comparison result of the 1st−block (2 nd−block, …, Bth−block) may be equal. Then TP2 asks Pi to prepare \({X}_{12}^{i,1}\) \(({X}_{12}^{i,2},\,\ldots ,\,{X}_{12}^{i,B})\).
Step 7. Pi performs the same processes as in Steps 2–4 to send \({X}_{12}^{i,1}({X}_{12}^{i,2},\,\ldots ,\,{X}_{12}^{i,B})\) to TP2.
Step 8. TP2 computes the comparison check of \({X}_{12}^{i,1}({X}_{12}^{i,2},\,\ldots ,\,{X}_{12}^{i,B})\), where for M = 3
for M > 3
If \(R={R}_{1}^{1}+{R}_{2}^{1}={R}_{1}^{2}+{R}_{2}^{2}=\ldots ={R}_{1}^{B}+{R}_{2}^{B}=0\), this means that X1, X2, …, XM are equal. Otherwise, X1, X2, …, XM are not equal. Note, participants check the result of the first block (\({R}_{2}^{1}\)) and if \({R}_{2}^{1}\) = 0 they continue to check the next block and so on until they reach the last block; otherwise, TP2 announces that the secrets are not equal.
Correctness
From Table 4, according to our initial preparation and encryption method, for every two bits we get two different encrypted bits, that is to say, we get Ca1 = 1 and X12 = 0 only when X1 = 0 and X2 = 0. So, the bit values of Ca1 and X12 together are decisive in determining the bit values of X1 and X2. Assume we have two participants Alice and Bob, and each participant has two bits X = 00 and Y = 10, respectively, and Krand = 00. Alice computes \({C}_{a1}={X}_{1}\oplus {X}_{1}^{\text{'}}={K}_{rand}^{1}\oplus {X}_{par{t}_{1}}\oplus {X}_{1}^{\text{'}}\) getting 1, and sends it to TP1. Bob also computes \({C}_{b1}={Y}_{1}\oplus {Y}_{1}^{\text{'}}={K}_{rand}^{1}\,\oplus {Y}_{part\_1}\oplus {Y}_{1}^{\text{'}}\) getting 1, and sends it to TP1. When TP1 computes R1 = Ca1 ⊕ Cb1 he gets R1 = 0, which means that the secrets of Alice and Bob may be equal or unequal (note if R1 = 1, TP1 announces that the secrets of Alice and Bob are not equal). So, they should move to the second-round to compare X12 and Y12.
In the second-round, Alice and Bob send \({X}_{12}={X}_{1}\oplus {X}_{2}={K}_{rand}^{1}\,\oplus {X}_{part\_1}\,\oplus {K}_{rand}^{2}\,\oplus {X}_{part\_2}\) and \({Y}_{12}={Y}_{1}\oplus {Y}_{2}={K}_{rand}^{1}\,\oplus {Y}_{part\_1}\,\oplus {K}_{rand}^{2}\,\oplus {Y}_{part\_2}\) to TP2, respectively. TP2 computes R2 = X12 ⊕ Y12 = 0 ⊕ 1 getting R2 = 1. TP1 then computes R = R1 + R2 getting R = 1, which means that X and Y are not equal. Thus, X and Y are equal if and only if R = R1 = R2 = 0. For example, suppose we have X = 0000 and Krand = 0000. Then X1 = 00 and X2 = 00. As shown in Table 5, we must get Ca1 = X1 ⊕ \({X}_{1}^{\text{'}}\) = 11 and X12 = 00 only when X1 = 00 and X2 = 00. Also, if we have Y = 0000 and Krand = 0000, then Y1 = 00 and Y2 = 00. Hence, we get Cb1 = Y1 ⊕ \({Y}_{1}^{\text{'}}\) = 11 and Y12 = 00. Now the two TPs can announce that the two inputs are equal by computing R = (Ca1 ⊕ Cb1) + (X12 ⊕ Y12) = 0, which proves the correctness of this protocol. Note that if we proposed that Ca1 = X2 ⊕ \({X}_{2}^{\text{'}}\) and Cb1 = Y2 ⊕ \({Y}_{2}^{\text{'}}\) instead of Ca1 = X1 ⊕ \({X}_{1}^{\text{'}}\) and Cb1 = Y1 ⊕ \({Y}_{1}^{\text{'}}\) respectively, we also get the same correct comparison result.
Here, we provide the necessary equations to verify the equality check by TP1 and TP2 for the various suggested protocols.
Two-party QPC with two rounds
From Eqs. (11) and (12), TP1 computes
From Eqs. (13) and (14), TP2 computes
In the proposed protocol, computing only R2 is not sufficient for getting the comparison result. For example, if we have X1 = X2 = 0, Y1 = Y2 = 1, and \({K}_{rand}^{1}={K}_{rand}^{2}=0\). Then R2 = 0 ⊕ 0 ⊕ 1 ⊕ 1 = 0. This means that X and Y are equal in contrast to the correct comparison result (R = R1 + R2 = 1 + 0 = 1). In such a case, R1 guarantees the correctness of the final result.
MDQPC with two rounds
From Eq. (15), for M = 3, TP1 computes
From Eq. (16), for M > 3, TP1 computes
In addition, from Eq. (17), for M = 3, TP2 computes
where \({K}_{rand}^{1}\) and \({K}_{rand}^{2}\) represent the random encryption keys for the first and second parts of the private information. Xi,part_1 and Xi,part_2 represent the first part and second part of the private information of Pi.
From Eq. (18), for M > 3, TP2 computes
Thus, if R1 = 0 and R2 = 0, R = R1 + R2 = 0, hence X1, X2, ..., XM are equal. Otherwise, X1, X2, ..., XM are not equal.
MDQPC with B-block
From Eq. (20), for M = 3, TP1 computes
So,
For M > 3,
So,
In addition, from Eq. (22), for M = 3, TP2 computes
where \({{\rm{K}}}_{rand}^{1,\,j}\) and \({{\rm{K}}}_{rand}^{2,\,j}\) are random subkeys for encrypting the first and second part of the jth block, j = 1, 2, …, B.
From Eq. (23) for M > 3, TP2 computes
So, we can get
Thus, if \({R}_{2}^{1}={R}_{2}^{2}=\cdots ={R}_{2}^{B}=0\), X1, X2, …, XM are equal. Otherwise, X1, X2, …, XM are not equal.
Security analysis
Here, we will show the robustness of the proposed QPC protocol against insider and outsider attacks. If the length of the secrets is odd, it should be modified. This process not only contributes to correctly executing the proposed protocol but also assists in enhancing the security of the protocol by altering the original secret bits without affecting the final comparison result. Moreover, two random keys are generated and distributed between TPs and participants to encrypt the private information of parties. As discussed in30,48, for improving the efficiency of the proposed DMQPC protocol, the private information of parties can be divided into several blocks of data. If the comparison result of a particular block is not equal, TP1 announces that the outcome of the comparison is not similar; hence there is no need to execute the remaining rounds. The three protocols in subsections 2.1, 2.4, and 2.5 are similar. Also, in the two-party QPC with two rounds, the quantum channel in the first-round is similar to the quantum channel in the second-round, so here we only analyze the quantum communication in the first-round between the participants and TP1.
Outside attack
In the two-party situation, Alice (Bob) sends \({S}_{a}^{\text{'}}\) (\({S}_{b}^{\text{'}}\)) to TP1, protected by single decoy photons la1 (lb1). Alice (Bob) then announces the measurement bases and the positions of all inserted decoy particles. Subsequently, the TP1 announces the measurement results of all embedded decoy particles. Alice (Bob) then checks the security of the communication by checking whether the measurement results of the decoy particles are correct. Since the outside attacker does not learn the measurement bases of the decoy particles and their positions ahead of time, the well-known attacks such as entangle-resend attacks32, correlation-elicitation attacks49, and intercept-resend attacks50 can be detected with nonzero probability51. For instance, if the eavesdropper, Eve, attempts to measure the decoy photons |0〉 or |1〉 in \({S}_{a}^{\text{'}}\) (\({S}_{b}^{\text{'}}\)) with the correct basis (e.g., Z-basis), she successfully passes the public eavesdropping check. But, If Eve attempts to measure the decoy photons |0〉 or |1〉 in \({S}_{a}^{\text{'}}\) (\({S}_{b}^{\text{'}}\)) with an incorrect basis (e.g., X-basis), she will be detected with a probability of 50%. The probability of choosing the wrong measuring basis is 50%. Thus, the rate of detecting Eve for each single decoy photon is 25% (i.e., 50% × 50%). Hence, the rate of detecting Eve for l single decoy photon is 1−(3/4)l, where |l| = |la1| = |lb1|. This rate approaches 1 when l is large enough. Furthermore, a Trojan-horse attack52 is prevented since photons are transmitted only once from participants to the TP1. So, our two-party QPC protocol is fully secure against outsider attacks. Since the proposed DMQPC protocol uses the same strategy as the two-party process, it is also secure against outsider attacks.
Participant’s attack
A significant advantage of our three different scenarios is that participant attacks such as collusion attack and cheating attack are not possible for the proposed protocols. Each participant receives two random keys from TP1 and TP2 for encrypting her/his secret without the participation or assistance of other parties. Therefore, there is no exchange of information or even communication among participants, and each participant sends the private information directly to the TP1 and TP2 through quantum channels. Thus, to steal confidential information, dishonest participants must adopt Eve’s attack strategies because they act as outside attackers. As discussed above, the protocol is secure against outside attacks.
TP’s attack
TP’s attack is another type of participant’s attack which could threaten the security of the protocol. Here we prove that our scheme is secure against dishonest or malicious TPs. Firstly, with the assumption that the two TPs are not allowed to collude together or with participants, our protocol is secure since the encrypted data is distributed to two independent TPs for computing the final comparison result. To clarify, assume we have a secret a and an encryption key b and c = a ⊕ b. The probability of an attacker to know a is \(\frac{1}{{2}^{n}}\), where n is the length of the secret a53. In the proposed protocol, from TP2’s point of view, as shown in Table 4, X12 = X1 ⊕ X2. From Eqs. (2) and (3), \({X}_{1}={K}_{rand}^{1}\,\oplus \,{X}_{part\_1}\) and \({X}_{2}={K}_{rand}^{2}\,\oplus \,{X}_{part\_2}\) where Xpart_1 is the first part of the secret message (X) and Xpart_2 is the second part of X. The probability of TP2 to know X is \(\frac{1}{{2}^{\frac{n}{2}}}\), where n is the length of the secret X, and \(\frac{n}{2}\) is the length of X12. When n is large enough, the probability of getting the secret data is negligible. In addition, according to Table 4, TP2 can obtain X12 = 1 ⊕ \({X}_{1}^{\text{'}}\). Hence, if X12 = 0 then TP2 can learn that \({X}_{1}^{\text{'}}\) = 1, otherwise \({X}_{1}^{\text{'}}\) = 0. However, the private information of Alice is still secure against TP2’s attack for two reasons: (1) TP2 cannot learn any private information of Alice using \({X}_{1}^{\text{'}}\); (2) the private information of Alice (Xpart_1 and Xpart_2) is protected by two random keys (\({K}_{rand}^{1}\) and \({K}_{rand}^{2}\)).
From TP1’s point of view, Alice sends her encrypted secret (i.e., Ca1 = X1 ⊕ \({X}_{1}^{\text{'}}\) (Ca2 = X2 ⊕ \({X}_{2}^{\text{'}}\))) to TP1. TP1 cannot reveal any useful information without knowing X1 or \({X}_{1}^{\text{'}}\) (X2 or \({X}_{2}^{\text{'}}\)). The probability of knowing the original secret is \(\frac{1}{{2}^{\frac{n}{2}}}\), where n is the length of the secret X, and \(\frac{n}{2}\) is the length of Ca1(Ca2). When n is large enough, the probability of TP1 to know the original secret is negligible. Also, when participants’ secret data is divided into B blocks, the probability of TP1(TP2) to identify the original secret is \({(\frac{1}{{2}^{((\frac{n}{B})/2)}})}^{B}\), where B is the number of blocks. In addition, according to Table 4, TP1 can obtain Ca1 = 1 ⊕ X2 and X2 = 1 ⊕ Ca1. Hence, if Ca1 = 0; then TP1 can learn that X2 = 1, otherwise X2 = 0. However, the private information of Alice (Xpart_1 and Xpart_2) is still secure against TP1’s attack, since \({X}_{part\_1}={X}_{1}\oplus {K}_{rand}^{1}\) and \({X}_{part\_2}={X}_{2}\oplus {K}_{rand}^{2}\).
Efficiency Analysis
The used qubit efficiency is defined as \(\eta =\frac{C}{q}\) 54,55,56, where C refers to all classical bits that can be transmitted, and q refers to the total number of used photons. In the two-party case, the proposed protocol is executed in one or two rounds depending on the first-round result. If the proposed protocol is executed in one round, both Alice and Bob prepare \(\frac{n}{2}\) single photons. The protocol is completed in one round when the comparison result of the first parts of Alice’s secret and Bob’s secret are not equal. Thus, the qubit efficiency is \(\frac{n}{\frac{n}{2}+\frac{n}{2}}\) (i.e., 100%). However, if the first parts of Alice’s secret and Bob’s secret are equal, the proposed protocol is executed in two rounds. Hence, the qubit efficiency is \(\frac{n}{2(\frac{n}{2}+\frac{n}{2})}\) (i.e. 50%). In the multi-party protocol with two rounds, the qubit efficiency of one round is \(\frac{n}{M\frac{n}{2}}\), and the qubit efficiency for the two rounds is \(\frac{n}{Mn}\). In the multi-party protocol with B blocks, the proposed protocol is executed in one or more blocks depending on the previous block result. Thus, the qubit efficiency is ranging from \(\frac{n}{M\,{r}_{n}}\) to \(\frac{n}{M\,n}\), where \({r}_{n}=\frac{n}{2B}\) is the number of bits in each round and B is the number of determined blocks. For example, consider four participants (M = 4) who would like to compare their secrets of length 12 bits (n = 12). In this case, they can divide the secret into 2, 3, or 6 blocks, each part containing 6 bits, 4 bits, or 2 bits, respectively. Assume that they choose to divide the secrets into 2 blocks (i.e., B = 2) and each block contains 6 bits (i.e., \(\frac{n}{B}=6\)); hence the \({r}_{n}=\frac{12}{4}=3\). Then the qubit efficiency ranges from 25% to 100%. It should be noted that the qubit efficiency increases or decreases depending on the number of participants and selected blocks. For comparison, in Liu and Wang’s protocol46, the qubit efficiency is \(\frac{n}{M(\frac{n}{2}+\frac{n}{2})}\), and for n = 12 and M = 4, the qubit efficiency is equal to 40%.
Comparison
Here we compare the performance of our DMQPC proposed scheme with previous MQPC schemes. We first compare our DMQPC protocol with Liu and Wang’s protocol46 (see Table 6). We then compare our DMQPC protocol with previous MQPC protocols.
Abulkasim et al.57 showed that the Liu-Wang protocol suffers from participant attack. In our proposed protocol, participant attack is not possible. Thus, our protocol is safe not only against well-known participant attacks but also against potential participant attacks. Both the Liu-Wang protocol and our protocol use single photon states as a quantum resource and perform single photon measurements. The Liu-Wang protocol uses one TP who performs single photon measurements. In our protocol, two TPs are adopted and they also perform single photon preparation and measurements.
Like the Liu-Wang protocol, in our scheme, both the TP and the participants prepare single photons for deducing the comparison result. Like the Liu-Wang protocol, our protocol is dynamic so that any new subset of M parties can join or leave the protocol at any time. However, in the Liu-Wang protocol, new participants have to participate in the protocol before the quantum states are measured. Unlike the Liu-Wang protocol, in our scheme, the TPs can compare the private information of any subset of M parties without any assistance from other parties. In contrary to the Liu-Wang protocol, our scheme reduces the cost of communication by half, in some situations, where the protocol can be executed in one round to get the final comparison result.
From Table 7, like the protocols in refs. 31,40,42,43,44,45,58, our protocol is secure against participant attack. In contrast with the proposed protocols in refs. 31,40,41,42,43,44,45,46, which suppose that there is a semi-honest TP who executes the QPC protocol loyally, our proposed protocol allows for almost-dishonest TPs. Unlike the protocols in refs. 31,40,41,42,43,44,45,46,58, our protocol is secure against a malicious TP1(TP2). Like the protocols in refs. 31,46, our protocol works in an environment where participants and TPs could be strangers, where there is no need for authenticated channels to prevent secret information from leaking. Compared to previous work, our main contribution is that participant attack is not possible in this work, since there is no exchange of information or even communication among participants. In addition, our scheme reduces the cost of communication.
Conclusion
This work proposes a novel dynamic multiparty quantum private comparison protocol that does not allow participant attack. The proposed protocol divides the private information into equal parts, and every participant independently encrypts her/his secrets using two random keys before sending them to two third parties using quantum channels. The protocol is executed in one or more rounds depending on the result of the previous round. The private information can also be divided into a number of blocks, with each block containing two equal parts of the secret. The dynamic nature of the proposed protocol enables the two TPs to compare the private information of any subset of M parties without any assistance from other parties. Any subset of M parties can join in or leave the protocol at any time without any extra conditions. Our analysis proves that the proposed protocol is correct and fully secure against outside attack. Furthermore, the scheme is not open to participant attacks. Compared to existing schemes, our protocol is more efficient, more secure and more feasible. Thus, our scheme is an ideal choice for comparing private information of M parties.
References
Bennett, C. H. & Brassard, G. Quantum cryptography: Public key distribution and coin tossing. Theor. Comput. Sci. 560, 7–11 (2014).
Shor, P. W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493 (1995).
Martin-Lopez, E. et al. Experimental realization of Shor’s quantum factoring algorithm using qubit recycling. Nat. Photo. 6, 773 (2012).
Politi, A., Matthews, J. C. & O’brien, J. L. Shor’s quantum factoring algorithm on a photonic chip. Science 325, 1221–1221 (2009).
Jin, X.-M. et al. Experimental free-space quantum teleportation. Nat. photo. 4, 376 (2010).
Yin, J. et al. Quantum teleportation and entanglement distribution over 100-kilometre free-space channels. Nature 488, 185 (2012).
Zhang, Q. et al. Experimental quantum teleportation of a two-qubit composite system. Nat. Phys. 2, 678 (2006).
Huang, Y.-F., Ren, X.-F., Zhang, Y.-S., Duan, L.-M. & Guo, G.-C. Experimental teleportation of a quantum controlled-NOT gate. Phys Rev Lett 93, 240501 (2004).
Ren, J.-G. et al. Ground-to-satellite quantum teleportation. Nature 549, 70 (2017).
Bennett, C. H. & Wiesner, S. J. Communication via one-and two-particle operators on Einstein-Podolsky-Rosen states. Phys Rev Lett 69, 2881 (1992).
Mattle, K., Weinfurter, H., Kwiat, P. G. & Zeilinger, A. Dense coding in experimental quantum communication. Phys Rev Lett 76, 4656 (1996).
Wang, C., Deng, F.-G., Li, Y.-S., Liu, X.-S. & Long, G. L. Quantum secure direct communication with high-dimension quantum superdense coding. Phys. Rev. A 71, 044305 (2005).
Hu, X.-M. et al. Beating the channel capacity limit for superdense coding with entangled ququarts. Sci. advances 4, eaat9304 (2018).
Deng, F.-G., Long, G. L. & Liu, X.-S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 68, 042317 (2003).
Chen, X.-B., Wang, T.-Y., Du, J.-Z., Wen, Q.-Y. & Zhu, F.-C. Controlled quantum secure direct communication with quantum encryption. Int. J. Quantum Inf 6, 543–551 (2008).
Farouk, A., Zakaria, M., Megahed, A. & Omara, F. A. A generalized architecture of quantum secure direct communication for N disjointed users with authentication. Sci. reports 5, 16080 (2015).
Hillery, M., Bužek, V. & Berthiaume, A. Quantum secret sharing. Phys. Rev. A 59, 1829 (1999).
Abulkasim, H., Hamad, S., El Bahnasy, K. & Rida, S. Z. Authenticated quantum secret sharing with quantum dialogue based on Bell states. Phys. Scr. 91, 085101 (2016).
Abulkasim, H., Hamad, S., Khalifa, A. & El Bahnasy, K. Quantum secret sharing with identity authentication based on Bell states. Int. J. Quantum Inf 15, 1750023 (2017).
Qin, H., Tang, W. K. & Tso, R. Rational quantum secret sharing. Sci. reports 8, 11115 (2018).
Abulkasim, H., Hamad, S. & Elhadad, A. Reply to Comment on ‘Authenticated quantum secret sharing with quantum dialogue based on Bell states’. Phys. Scr. 93, 027001 (2018).
Nguyen, B. A. Quantum dialogue. Phys. Lett. A 328, 6–10 (2004).
Zhou, N.-R., Li, J.-F., Yu, Z.-B., Gong, L.-H. & Farouk, A. New quantum dialogue protocol based on continuous-variable two-mode squeezed vacuum states. Quantum Inf Process 16, 4 (2017).
Zhou, N., Zeng, G. & Xiong, J. Quantum key agreement protocol. Electron. Lett. 40, 1149–1150 (2004).
Cao, H. & Ma, W. Multi-party traveling-mode quantum key agreement protocols immune to collusive attack. Quantum Inf Process 17, 219 (2018).
Yao, A. C. In Foundations of Computer Science, 1982. SFCS'08. 23rd Annual Symposium on. 160–164 (IEEE).
Boudot, F., Schoenmakers, B. & Traore, J. A fair and efficient solution to the socialist millionaires’ problem. Discrete Appl. Math. 111, 23–36 (2001).
Lin, H.-Y. & Tzeng, W.-G. In International Conference on Applied Cryptography and Network Security. 456–466 (Springer).
Lo, H.-K. Insecurity of quantum secure computations. Phys. Rev. A 56, 1154 (1997).
Yang, Y.-G. & Wen, Q.-Y. An efficient two-party quantum private comparison protocol with decoy photons and two-photon entanglement. J Phys A-Math Theor 42, 055305 (2009).
Hung, S.-M., Hwang, S.-L., Hwang, T. & Kao, S.-H. Multiparty quantum private comparison with almost dishonest third parties for strangers. Quantum Inf Process 16, 36 (2017).
Gao, F., Qin, S.-J., Wen, Q.-Y. & Zhu, F.-C. A simple participant attack on the brádler-dušek protocol. Quantum. Inf. Comput. 7, 329–334 (2007).
Zhang, W.-W. & Zhang, K.-J. Cryptanalysis and improvement of the quantum private comparison protocol with semi-honest third party. Quantum Inf Process 12, 1981–1990 (2013).
Jiang, L., He, G., Nie, D., Xiong, J. & Zeng, G. Quantum anonymous voting for continuous variables. Phys. Rev. A 85, 042309 (2012).
Xue, P. & Zhang, X. A simple quantum voting scheme with multi-qubit entanglement. Sci. reports 7, 7586 (2017).
Muhammad, S. et al. Quantum bidding in Bridge. Phys. Rev. X 4, 021047 (2014).
Hogg, T., Harsha, P. & Chen, K.-Y. Quantum auctions. Int. J. Quantum Inf 5, 751–780 (2007).
Zhang, R., Shi, R.-h, Qin, J.-q & Peng, Z.-w An economic and feasible Quantum Sealed-bid Auction protocol. Quantum Inf Process 17, 35 (2018).
Zhao, Z., Naseri, M. & Zheng, Y. Secure quantum sealed-bid auction with post-confirmation. Opt Commun 283, 3194–3197 (2010).
Chang, Y.-J., Tsai, C.-W. & Hwang, T. Multi-user private comparison protocol using GHZ class states. Quantum Inf Process 12, 1077–1088 (2013).
Luo, Q.-b, Yang, G.-w, She, K., Niu, W.-n & Wang, Y.-q Multi-party quantum private comparison protocol based on d-dimensional entangled states. Quantum Inf Process 13, 2343–2352 (2014).
Ye, T.-Y. Multi-party quantum private comparison protocol based on entanglement swapping of Bell entangled states. Commun. Theor. Phys. 66, 280 (2016).
Huang, S.-L., Hwang, T. & Gope, P. Multi-party quantum private comparison protocol with an almost-dishonest third party using GHZ states. Int. J. Theor. Phys. 55, 2969–2976 (2016).
Zhao-Xu, J. & Tian-Yu, Y. Multi-party quantum private comparison based on the entanglement swapping of d-level cat states and d-level Bell states. Quantum Inf Process 16, 177 (2017).
Ye, T. & Ji, Z. Multi-user quantum private comparison with scattered preparation and one-way convergent transmission of quantum states. Sci. China Phys. Mech. Astron. 60, 090312 (2017).
Liu, W. & Wang, Y.-B. Dynamic multi-party quantum private comparison protocol with single photons in both polarization and spatial-mode degrees of freedom. Int. J. Theor. Phys. 55, 5307–5317 (2016).
Hu, J.-Y. et al. Experimental quantum secure direct communication with single photons. Light Sci. Appl. 5, e16144 (2016).
Li, J., Jia, L., Zhou, H.-F. & Zhang, T.-T. Secure quantum private comparison protocol based on the entanglement swapping between three-particle W-class state and bell state. Int. J. Theor. Phys. 55, 1710–1718 (2016).
Fei, G., Song, L., Qiao-Yan, W. & Fu-Chen, Z. A special eavesdropping on one-sender versus N-receiver QSDC protocol. Chinese Phys. Lett. 25, 1561 (2008).
Lin, J., Tseng, H.-Y. & Hwang, T. Intercept–resend attacks on Chen et al.’s quantum private comparison protocol and the improvements. Opt Commun 284, 2412–2414 (2011).
Cai, Q.-Y. Eavesdropping on the two-way quantum communication protocols with invisible photons. Phys. Lett. A 351, 23–25 (2006).
Gisin, N., Fasel, S., Kraus, B., Zbinden, H. & Ribordy, G. Trojan-horse attacks on quantum-key-distribution systems. Phys. Rev. A 73, 022320 (2006).
Sun, Z., Yu, J., Wang, P., Xu, L. & Wu, C. Quantum private comparison with a malicious third party. Quantum Inf Process 14, 2125–2133 (2015).
Chen, J.-H., Lee, K.-C. & Hwang, T. The enhancement of Zhou et al.‘s quantum secret sharing protocol. Int. J. Mod. Phy. C 20, 1531–1535 (2009).
Ting, X. & Tian-Yu, Y. Cryptanalysis and Improvement for the Quantum Private Comparison Protocol Based on Triplet Entangled State and Single-Particle Measurement. Int. J. Theor. Phys. 56, 771–780 (2017).
Hwang, T. & Lee, K.-C. EPR quantum key distribution protocols with potential 100% qubit efficiency. IET Inf. Secur. 1, 43–45 (2007).
Abulkasim, H. et al. Improved Dynamic Multi-Party Quantum Private Comparison for Next-Generation Mobile Network. IEEE Access 7, 17917–17926 (2019).
Zhou, Y.-H., Shi, W.-M. & Yang, Y.-G. Comment on “Efficient and feasible quantum private comparison of equality against the collective amplitude damping noise”. Quantum Inf Process 13, 573–585 (2014).
Author information
Authors and Affiliations
Contributions
Abulkasim, H. designed the scheme. Abulkasim, H., Farouk, A., Hamad, S., Mashatan, A. and Ghose, S. did security analysis and comparisons. Abulkasim, H. and Farouk, A. prepared all tables and figures. All authors contributed to the writing and discussion of the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abulkasim, H., Farouk, A., Hamad, S. et al. Secure dynamic multiparty quantum private comparison. Sci Rep 9, 17818 (2019). https://doi.org/10.1038/s41598-019-53967-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-53967-9
This article is cited by
-
RETRACTED ARTICLE: Application of single frame image super-resolution algorithm based on generative adversarial network in tennis motion image resolution
Journal of Ambient Intelligence and Humanized Computing (2022)
-
RETRACTED ARTICLE: Innovation performance of listed companies based on machine computing and data envelopment analysis
Journal of Ambient Intelligence and Humanized Computing (2022)
-
RETRACTED ARTICLE: Analysis of household green food consumption behavior based on machine learning prediction
Journal of Ambient Intelligence and Humanized Computing (2022)
-
Security improvements for privacy-preserving quantum multiparty computation based on circular structure
Quantum Information Processing (2022)
-
RETRACTED ARTICLE: Research on traditional art digitization based on machine learning and image recognition
Journal of Ambient Intelligence and Humanized Computing (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.