Abstract
We examine the influence of superconductivity on the magneto-transport properties of a ferromagnetic Ni nanowire connected to Nb electrodes. We show experimentally and confirm theoretically that the Nb/Ni interface plays an essential role in the electron transport through the device. Just below the superconducting transition, a strong inverse proximity effect from the nanowire suppresses superconducting correlations at Nb/Ni interfaces, resulting in a conventional anisotropic magneto-resistive response. At lower temperatures however, the Nb electrodes operate as superconducting shunts. As the result, the magneto-resistance exhibits a strongly growing hysteretic behavior accompanied by a series of saw-like jumps. The latter are associated with the penetration/escape of individual Abrikosov vortices that influence non-equilibrium processes at the Nb/Ni interface. These effects should be taken into account when designing superconducting quantum nano-hybrids involving ferromagnetic nanowires.
Similar content being viewed by others
Introduction
Magneto-transport and magneto-dynamic properties of ferromagnetic (F) nanowires (NWs) currently attract a great interest due to their strong magnetic anisotropy and various size and spin effects1,2. These phenomena make F-NWs promising for applications in functional hybrid nano-devices, such as superconducting phase inverters, spin gates, magnetic memory elements3,4,5,6,7,8,9, etc. Usually, F-NWs are integrated into electronic circuits in which they are connected to normal-metal electrodes10,11,12,13,14,15,16,17,18. Magneto-resistive (MR) effects in such conventional circuits are dominated by the so-called anisotropic magneto-resistance (AMR), due to the anisotropy of the spin-orbit scattering in F-NWs19. As a result, the MR of the F-NW depends on the angle between the current and the magnetization, thus enabling one to correlate the magnetic state of the F-NW to its resistance12,13,14,17,19.
Recently a qualitatively new type of circuit has emerged, in which F-NWs are bonded to superconducting (S) electrodes18,20. In ref.18 an outstandingly long-range proximity phenomenon was reported: a Josephson effect between two W banks linked together by a 0.6 μm long ferromagnetic Co-NW. In general, this domain of activity is motivated by a search for novel quantum properties of F-NW-based superconducting hybrids. Here we study the longitudinal MR of a S/F-NW/S hybrid device made of Ni-NW bonded to Nb superconducting electrodes. We demonstrate that below the superconducting transition temperature of Nb electrodes, the MR of the device is heavily dominated by the phenomena occurring at the Nb/Ni interface, where the superconducting Nb-electrodes operate as electric shunts of the Ni-NW. As a result, a hysteretic MR is observed on the top of a conventional AMR response. We also observed a series of quasi-periodic saw-like behavior in the MR signal, a direct consequence of the penetration of individual magnetic flux quanta - Abrikosov vortices from Nb/Ni interface into the superconducting electrodes. We suggest a model that explains the observed phenomena and the unusually high sensitivity of our S/F-NW/S device to the magnetic flux.
Results and Discussion
Resistivity near the superconducting transition
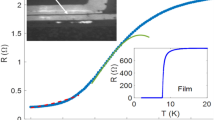
The resistance measured with 4-probes has a temperature dependence presented with blue dots in Fig. 1b. The resistance remains almost constant down to 6.7 K. Below this temperature it rapidly lowers but does not undergo a full transition to the superconducting state; the resistance remains relatively high even at 4 K. Additional 2-probe measurements confirmed (see Supplementary Materials) that the superconducting transition in Nb takes place at TCNb = 8.3 K, as expected. However, due to a strong inverse proximity effect from the F-NW the superconductivity of Nb electrodes near the Nb/Ni interface is suppressed; the resistance REl of the Nb/Ni interface remains almost unchanged. Only at a significantly lower temperature TC ≃ 6.7 K the interface resistance starts to decrease, witnessed by a major drop of the 2-probe resistance (see Supplementary Materials). The total resistance of the studied device comprises the resistance RNi of the Ni-NW itself, and the two Nb/Ni interface resistances REl. In the next subsection we evaluate the total resistance of the device and the temperature dependence of REl.
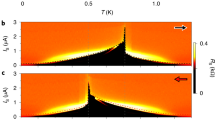
(a) Scanning Electron Microscopy image of the studied S/F-NW/S structure: Ni nanowire is coupled to four planar Nb electrodes. In the 4-probe measurements left and right electrodes serve for the current injection, and the two middle electrodes as voltage contacts. In the 2-probe experiments the middle electrodes are used as both voltage and current contacts. (b) Blue data points: R(T) dependence measured at Isam = 30 μ A with the 4-probe scheme. Red dashed line: a fit using the effective resistance model. Sketch: the effective resistance circuit of the of the Nb/Ni-NW interface (see in the text). (c) Sketches of the current distribution in the overlapping region between Ni-NW and Nb voltage electrodes in the 4-probe experiment (see Supplementary Materials). Left - in the normal state of the Nb layer; center - in the superconducting state; right: a zoomed sketch of the current distribution at the edge of Nb/Ni interface. The superconducting current lines are depicted in blue, the normal current lines are in red. (d,f) Magneto-resistance R(H) measured at T = 10 K and 4.2 K, respectively. Insets: hysteresis loops due to the Ni-NW magnetization switching at ±0.076 T. Red dashed ellipses at (d) point to specific regions in R(H) where the Abrikosov vortex penetration causes a series of peaks in the magneto-resistance. (e) A sketch of the vortex penetration into Nb-electrodes at the Nb/Ni interface in the vicinity of the electrode’s edges (see in the text).
Current flow at the Nb/Ni interface
The current flow in the overlapping Nb/Ni regions strongly depends on the state, normal or superconducting, of Nb-layer. In the normal state of Nb, the current distribution can be found from the solution of the Laplace equation for a scalar potential. This distribution is schematically shown on the left panel of Fig. 1c. Below the “effective” critical temperature TC ≈ 6.7 K, at which the superconducting correlations in Nb start to affect the resistance near Nb/Ni interface, the current density is substantially redistributed (central panel in Fig. 1c). In the vicinity of the Nb/Ni interface the normal current is converted to supercurrent. This conversion takes place essentially in a narrow region at the inlet edge of the overlapping region (right panel in Fig. 1c). In the overlapping region, the current flowing through the NW splits, a part of which running into the superconducting Nb, which works as a superconducting shunt. There is no normal current flow in the central part of Ni-NW. Finally, an inverse conversion from supercurrent to the normal current takes place at the outlet edge of the overlapped region. As a result, the edge regions give an essential contribution to the interface resistance REL, since both normal and supercurrent coexist.
In the 4-probe method the voltage difference is measured between two superconducting parts of Nb shunts. Considering two identical current conversions, one at the outlet edge of the first voltage lead and other at the inlet of the second one, the measured resistance R = V/I is:
where the resistance of the Ni-NW is:
here, lNW = 380 nm is the distance between middle Nb/Ni electrodes, ρNi is Ni resistivity, d = 107 nm is the diameter of the nanowire, and REL is the effective resistance of one Nb/Ni electrode.
To find REL we subdivide the inlet and outlet areas of the Nb/Ni film in small blocks of a length Δl. The Ni-part of this block has resistance
These Ni-parts connect to the superconducting Nb-shunt via an effective resistance of the current conversion area,
where ρB is the specific Nb/Ni interface resistance.
The resistance of the inlet and outlet areas of the Nb/Ni electrodes REL can then be modeled as semi-infinite chain of resistances RB and RNW, as represented in the inset of Fig. 1b. In this scheme the upper wire represents Nb-shunt. As a result, the total resistance REL is equal to the resistance of RB and the sum RNW + REL connected in parallel, as it is schematized in the inset of Fig. 1b:
From (5) we get
In the limit Δl → 0 from expression (6) we finally have
We now evaluate the temperature dependence of the interface resistivity ρB. Due to the inverse proximity effect the superconducting gap of Nb is strongly suppressed at Nb/Ni interface; inside the Nb electrode it is restored to its bulk value only at a distance of the order of the temperature-dependent Ginsburg-Landau coherence length ξGL(T) = (π/2)ξNb(1 − T/TC)−1/2, where ξNb = (ℏD/2πkBTC)1/2, D is the diffusion coefficient. On a microscopic level, the conversion of the normal current into the superconducting current occurs due to Andreev reflection of quasiparticles from the wall of the potential barrier formed by the coordinate-dependent gap in the spectrum of the elementary excitations of Nb. As a result, the normal quasiparticles carrying the normal current are trapped in the region of the order of ξGL(T) in the vicinity of Nb/Ni interface. This allows one to estimate the temperature dependence of the interface resistivity:
In more advanced models21,22,23 the interface resistance has the temperature dependence \({\rho }_{B} \sim {(1-T/{T}_{C})}^{-\alpha }\), where α is indeed close to 0.5; its precise value is decided by characteristic quasiparticle energy relaxation processes in the superconductor. As a precise determination of the proportionality coefficient in the expression (8) is a difficult task, we combined (7) and (8) to REL = 0.5A(1 − T/TC)−1/4, and used the following expression to fit the observed temperature dependence of the total resistance:
where RNi and A are the fitting parameters. This expression follows directly from (1) and explicitly takes into account the temperature dependence of the REL in (1). The best fit (red line in Fig. 1b) has been achieved with RNi ≈ 1.8 Ω and A ≈ 1.2 Ω. The first value fixes the resistivity of our Ni-NW to ρNi ≈ 4.26 μΩ cm, in agreement with the results of previous experiments on Ni-NW based structures measured at the liquid helium temperatures16,24.
In fact, the fitting parameters correspond to independent physical quantities. The first of these parameters, RNi is fully determined by the geometry of the nanowire and by its resistivity. The second fitting parameter A, according to Eqs (7 and 8) also depends on the boundary resistance of Nb-Ni interface. The magnitude of this parameter determines the length of conversion of a normal current into a supercurrent.
We can evaluate the characteristic scale lleak of the current leakage into Ni wire from the Nb/Ni electrode. It can be done from (3) and (4) by equating resistances RNW = RB, at which lleak ≈ Δl. We get:
at T = 4.2 K, that is an order of magnitude smaller the width of Nb electrodes visible in Fig. 1a.
The agreement of the fit with the experimental data confirms the assumption of the model that conversion of a normal current to supercurrent is mostly due to Andreev reflection processes at Nb-Ni interface, while the processes of high-energy quasiparticle relaxation are negligible.
Magneto-transport: general behavior
Small length scale of conversion at the edges of the overlapping regions, of a normal current flowing in Ni-NW into a supercurrent in the Nb-shunt has important consequences for the magneto-transport properties of the device. The longitudinal magneto-resistance R(H) signals measured at 4.2 K (T < TC) and at 10 K (T > TC) are presented in Fig. 1d,f, respectively.
When Nb-electrodes are in the normal state, T > TC, the magnetic field uniformly enters the sample, Fig. 2a. R(H) follows a conventional AMR12,14,19,25. Upon the magnetic field cycling R(H) shows a hysteresis due to the Ni-NW magnetization switches at a coercive field Hc = ±0.076T. The magneto-resistance does not exceed 0.7% in the entire field range 0–1.5T. At H = Hc R(H) jumps are ΔRM ~ 0.015 Ω, that is about 3% of the average resistance (inset in Fig. 1f).
Device behavior at different external magnetic fields and temperatures. (a) T > TC, the magnetic field (presented by a series of black arrows) uniformly enters the sample. There is no screening current. (b) T < TC, at Hc < H < Hc1 the magnetic field is expelled owing to screening Meissner currents (blue arrows) flowing along the edges of Nb-electrodes; it is focused in the nanowire. The screening current flow is strongly modified near Nb/Ni-interface. (c) An Abrikosov vortex penetrates inside Nb-electrode from Nb/Ni interface. (d) Enlarged picture of resistance jumps, marked by arrows, on R(H) dependence at T = 4.2 K, these jumps are almost equidistant. (e) Statistics of the magneto-resistance jumps visible in Figs 1d and 2d as a function of the applied field changing in different sweep directions.
At T = 4.2 K, when the superconducting correlations from Nb reach Nb/Ni interface, T < TC < TCNb, the magneto-resistive behavior of the device changes drastically, Fig. 1d. R(H) grows rapidly and almost linearly from R = 3.33 Ω to R = 3.73 Ω, that is about 11% of variation in the entire field range 0–1.5 T. R(H) shows a hysteretic field response; the difference in the resistivity between R(H) branches measured in ascending and descending magnetic fields reaches ≃0.05 Ω at H = 0.7 T. Importantly, R(H) curves are saw-shaped (in the regions marked by dashed ellipses in Fig. 1d) with rather regular resistivity jumps by up resistivity drops of up to ΔRV ≃ 0.05 Ω. The amplitude of these drops is larger than the whole AMR observed at 10 K. In addition, AMR jumps of ΔRM ≃ 0.01 Ω associated with magnetization of the F-NW and AMR phenomenon remain (see inset in Fig. 1d). Notice however, that the relative AMR R(H) variation at Hc is smaller as compared to the high temperature behavior, Fig. 1f.
Since the magnetic switching of the Ni-NW leads to only tiny variations of R(H) (see inset in Fig. 1d), the main MR features in Fig. 1d should be intimately related to phenomena occurring near Nb/Ni interface. The resistance of these regions is mostly determined by non-equilibrium processes of the conversion of the normal current to supercurrent and back21,22,23. In our estimates, at T = 4.2 K and H = 0 the conversion takes place on the length ≈160 nm (10), resulting in the interface resistance of 1–3 Ω. The latter depends significantly on the suppression of the superconducting correlations in the vicinity of the NW.
When an external magnetic field is applied along the NW, the Meissner screening currents jS start to circulate (blue lines in Fig. 2b). In an increasing field they progressively suppress the superconducting correlations in the vicinity of the Nb/Ni interface and provoke a growth of the conversion length. As a result, the interface resistance increases. This explains the general increase in R(H) behavior seen in Fig. 1d.
Magneto-transport: signatures of Abrikosov vortices
We now discuss the puzzling features - sudden resistance jumps observed in the R(H) curves in the regions marked by ellipses in Fig. 1d. The zoom of this curve is demonstrated on Fig. 2d. These jumps are related to the Abrikosov vortex penetration into the device, as we discuss below. When the applied field exceeds the first critical field Hc1 of Nb, a mixed superconducting state with Abrikosov vortices becomes energetically favorable. As Meissner screening currents jS also increase with the magnetic field, they weaken the superconducting order at the edges of Nb and facilitate the vortex penetration. The weakest edge region from which the vortices can penetrate is located close to Nb/Ni interface where the superconducting order is further suppressed due to the proximity with Ni-NW (Fig. 2b).
The penetration of a single vortex into Nb partially relaxes both the magnetic energy and the screening Meissner currents26. The latter effect is especially important near the Nb/Ni interface, due to a peculiar geometry of the device (see Fig. 2c). A sudden reduction of the screening currents partially restores the superconducting correlations near Nb/Ni interface and reduces the conversion length. A drop ΔRV in the interface resistance occurs. Upon further increase of the field, the screening currents start to grow again until another vortex enters. The process continues and results in a series of sudden resistance jumps observed in R(H), Figs 1d and 2e, each jump witnessing for the penetration of one single quantum vortex into Nb-electrode.
As seen in Figs 1d and 2e the jumps ΔRV(H) appear nearly periodic; they indeed can be associated to individual vortex penetration. It is not clear however, if the device detects all vortices one by one. A simple estimate of the total number of vortices penetrated into the sample at a field H can be done and compared to the statistics of the observed events, presented in Fig. 2e. Due to the device geometry, the area S into which Abrikosov vortices penetrate from a given injection point is of the order of \(S \sim {h}^{\ast }\times {\lambda }_{Nb}\) = 1.4 × 104 nm2, where \({h}^{\ast }\simeq h-2{\xi }_{GL}\simeq 180\,{\rm{nm}}\) is the effective thickness, and \({\lambda }_{Nb}\simeq 80\,{\rm{nm}}\) is the London penetration depth in our granular Nb-film at T = 4.2 K. At a field H there should be around \(N=(S/{\Phi }_{0})\times H \sim \)10–20 × H[T] Abrikosov vortices (in this estimation Φ0 is the magnetic flux quantum, the diamagnetic screening is neglected). Therefore, if the two electrodes are perfectly identical, the vortices penetrate into them simultaneously, and one would expect to count 10–20 jumps per Tesla. If the contacts are slightly different, then one ΔRV jump corresponds to the penetration of either one or two vortices, and the expected number of events per Tesla could be 10–40. The black line in Fig. 2e which matches the event statistics has the slope 28 × H[T], within the estimated numbers. This witnesses for the capacity of the device to detect individual quantum vortices.
Despite the quantum origin of the vortices and the resulting flux quantization, the resistance jumps ΔRV are not regular: they have different amplitudes and a slightly aperiodic occurrence in the rising/lowering field. There are several reasons for such “irregular” behavior. Indeed, once entered into Nb-electrode, the vortices leave the interface area. Their equilibrium location in Nb depends on the presence of other vortices in the neighborhood, surface and bulk defects etc. The resistance jumps are stronger for vortices propagated far away from the interface, and smaller for vortices remained in the vicinity. The same explanation applies to the hysteresis in R(H), and can be satisfactorily interpreted with the Bean critical state model27,28. Within this scenario, the end of hysteresis on R(H) curve in Fig. 1d at \(H\simeq 1{\rm{T}}\) corresponds to the so-called superconducting irreversibility field29,30,31. Other than the amplitude ΔRV of the jumps, their periodicity in the field is also affected by the presence of other vortices inside the device, defects etc. Finally, we should bear in mind that the 4-probe resistance comprises the sum of the inlet and outlet Nb/Ni interface resistances that were considered equal in (1). In real devices, the contacts have slightly different characteristics, resulting in vortices penetrating at different values of the external field. The drops in the total R(H) signal represent a sum of the two series of events.
Magneto-transport: peak effect near the normal state of the interface
Figure 3a shows R(H) curves measured at T = 6 K, that is in the middle of the resistive transition (marked by a red circle in Fig. 1b). In the increasing magnetic field branch, the resistance grows rapidly and saturates at the normal state resistance value at \(H\simeq \pm \,0.8\,{\rm{T}}\). This indicates that the field efficiently weakens the superconducting correlations at Nb/Ni interface and renders neighboring parts of the Nb-electrodes non-superconducting. The AMR jumps at Hc (inset in Fig. 3a) still exist but the hysteresis in R(H) curves vanishes. Also, ΔRV jumps associated with the vortex penetration/escape are not detected anymore. The main reason is that, unlike at T = 4.2 K, the effective S/N boundary at which the Abrikosov vortices are formed and penetrate into superconductor is pushed far away from the actual Nb/Ni interface region deeper into Nb.
(a) Magnetoresistance R(H) measured at T = 6 K. The inset shows magnified R(H) curves in the vicinity of Hc. Red and blue colors correspond to positive and negative sweep of the magnetic field. Arrows indicate direction of nanowire magnetization reversal. (b) Evolution of the temperature dependencies of resistance of the Ni nanowire for different applied magnetic fields. The peak effect close to TC could be related to the spin accumulation at the Nb/Ni interface (see explanation in the text).
A puzzling peak is observed in the field interval \(H\simeq \pm \)(0.5–0.6) T at which R(H) drops by ~0.05 Ω. A similar drop in the vicinity of the transition to the normal state is observed on R(T) curves in the interval of several tenths of Kelvin, as shown in Fig. 3b for R(T) measured at various fields. This phenomenon is washed out at zero field H = 0 but is present at other fields.
The origin of this effect is the spin-polarization process in the nanowire which leads to spin accumulation at the boundary. While the current inside Ni-NW is spin-polarized, the supercurrent in superconducting Nb-electrode is spinless. That means that only spinless part of incoming current can be converted to supercurrent, leading to spin accumulation at the boundary32,33. As a result, part of current turns out to be redistributed from Nb into the Ni-nanowire, leading to increase of the total resistance. The amplitude of resistance peak depends on the rate of spin-flip processes inside NW. At H = 0 the presence of domain walls leads to increase in spin-less component which able to leakage into superconducting electrodes. At H > 0 the number of domain walls decreases and as the result the rate of spin-flip intensity rises, thus, the resistance drops appear.
Conclusion
To conclude, we investigated experimentally and theoretically the electron transport properties of Ni-nanowires coupled to superconducting Nb-electrodes. We showed that the Superconductor-Ferromagnet interface plays an essential role in the magneto-resistive behavior of the device. Several effects related to the nano-scale phenomena at this interface were observed and explained. At temperatures just below the superconducting transition of Nb a strong inverse proximity effect from Ni-nanowire dominates the magnetic response, preserving a conventional anisotropic magneto-resistance measured at higher temperatures. At temperatures well below 6 K however, the superconducting order strengthens, and the Nb-electrodes play the role of superconducting shunts in the overlapped Nb/Ni areas of the device. This leads to a strong magneto-resistance that shows a well-pronounced hysteresis. The most intriguing feature is a series of jumps in the magneto-resistance related to the penetration of individual Abrikosov vortices through the Nb/Ni interface. At intermediary temperatures ~6 K the hysteresis and vortex-triggered magneto-resistivity jumps are washed out. Additional peaks appear in the vicinity of the critical transition. They are associated with non-equilibrium processes at the Nb/Ni interface. Similar peak features are observed on R(T) curves in the vicinity of critical temperature at non-zero fields. Importantly, the anisotropic magneto-resistance of the nanowire exists at all temperatures. This provides an opportunity to develop novel cryogenic hybrid nano-devices which take advantage of both anisotropic magneto-resistance and complex phenomena revealed at the Superconductor/Ferromagnet interface.
Methods
Nickel nanowires of 100–150 nm in diameter were obtained by templated electro-deposition into a porous anodic alumina34,35, extracted, washed, and dispersed in heptane (see Supplementary Materials). Individual NWs were bonded to Nb-electrodes for 4-probe transport measurements, following the steps comprising a seeding onto a marked Si/SiO2 substrate, electron lithography, magnetron sputtering, and lift-off processes (see Supplementary Materials and36). A set of samples was fabricated with different distances between inner (voltage) electrodes and with NWs of different diameters. They showed a qualitatively similar behavior. The device we discuss in this work was made using a 107 nm thick Ni-NW. The SEM image of the sample is shown in Fig. 1a. The distance between the two voltage electrodes is 380 nm. Both 4-probe and 2-probe transport measurements were provided. In all measurements the applied current was Isam = 30 μA. A magnetic field up to 1.5T was applied in the direction parallel to the Ni-NW main axis.
References
Todorovic, M., Schultz, S., Wong, J. & Scherer, A. Writing and reading of single magnetic domain per bit perpendicular patterned media. Appl. Phys. Lett. 74, 2516 (1999).
Poli, N. et al. Spin injection and relaxation in a mesoscopic superconductor. Phys. Rev. Lett. 100, 136601 (2008).
Feofanov, A. K. et al. Implementation of superconductor/ferromagnet/ superconductor π-shifters in superconducting digital and quantum circuits. Nature Physics 6, 593–597 (2010).
Jedema, F. J., Nijboer, M. S., Filip, A. T. & van Wees, B. J. Spin injection and spin accumulation in all-metal mesoscopic spin valves. Phys. Rev. B 67, 085319 (2003).
Larkin, T. I. et al. Ferromagnetic Josephson switching device with high characteristic voltage. Appl. Phys. Lett. 100, 222601 (2012).
Eschrig, M. Spin-polarized supercurrents for spintronics: a review of current progress. Rep. Prog. Phys. 78, 104501 (2015).
Linder, J. & Robinson, J. W. A. Superconducting spintronics. Nature Physics 11, 307 (2015).
Blamire, M. G. & Robinson, J. W. A. The interface between superconductivity and magnetism: understanding and device prospects. J. Phys.: Condens. Matter 26, 453201 (2014).
Soloviev, I. I. et al. Beyond Moore’s technologies: operation principles of a superconductor alternative. Beilstein Journal of Nanotechnology 8, 2689–2710 (2017).
Wernsdorfer, W. et al. Nucleation of magnetization reversal in individual nanosized nickel wires. Phys. Rev. Lett. 77, 9 (1996).
Chen, Y.-J., Hsu, J.-H. & Lin, H.-N. Fabrication of metal nanowires by atomic force microscopy nanoscratching and lift-off process. Nanotechnology 16, 1112–1115 (2005).
Bongyoung, Y., Youngwoo, R., Beyermann, W. P. & Myung, N. V. Magnetically assembled 30 nm diameter nickel nanowire with ferromagnetic electrodes. Nanotechnology 17, 2512–2517 (2006).
Ou, M. N. et al. Thermal and electrical transport properties of a single nickel nanowire. Phys. Stat. Sol. (b) 244, 4512–4517 (2007).
Rheem, Y., Yoo, B.-Y., Beyermann, W. P. & Myung, N. V. Electro- and magneto-transport properties of a single CoNi nanowire. Nanotechnology 18, 125204 (2007).
Walton, A. S. et al. Four-probe electrical transport measurements on individual metallic nanowires. Nanotechnology 18, 065204 (2007).
Venkata Kamalakar, M., Raychaudhuri, A. K., Wei, X., Teng, J. & Prewett, P. D. Temperature dependent electrical resistivity of a single strand of ferromagnetic single crystalline nanowire. Appl. Phys. Lett. 95, 013112 (2009).
Kimling, J., Gooth, J. & Nielsch, K. Anisotropic magnetothermal resistance in Ni nanowires. Phys. Rev. B. 87, 094409 (2013).
Wang, J. et al. Interplay between superconductivity and ferromagnetism in crystalline nanowires. Nature Physics 6, 389–394 (2010).
Wegrowe, J.-E., Kelly, D., Franck, A., Gilbert, S. E. & Ansermet, J.-P. Magnetoresistance of ferromagnetic nanowires. Phys. Rev. Lett. 82, 3681 (1999).
Kompaniiets, M. et al. Proximity-induced superconductivity in crystalline Cu and Co nanowires and nanogranular Co structures. J. App. Phys. 116, 073906 (2014).
Artemenko, S. N., Volkov, A. F. & Zaitsev, A. V. On the contribution of the superconductor to the resistance of a superconductor-normal metal system. J. Low Temp. Phys. 30, 487–502 (1978).
Krahenbuhl, Y. & Watts-Tobin, R. J. Microscopic theory of the current-voltage relationship across a normal-superconducting interface. J. Low Temp. Phys. 35, 569–591 (1979).
Hsiang, T. Y. & Clarke, J. Boundary resistance of the superconducting-normal interface. Phys. Rev. B 21, 945 (1980).
Kamalakar, M., Venkata & Raychaudhuri, A. K. Low temperature electrical transport in ferromagnetic Ni nanowires. Phys. Rev. B. 79, 205417 (2009).
Kozlov, S. N. et al. Magnetoresistance of a single polycrystalline nickel nanowire. J. Appl. Phys. 125, 063902 (2019).
Cren, T., Fokin, D., Debontridder, F., Dubost, V. & Roditchev, D. Ultimate vortex confinement studied by scanning tunneling spectroscopy. Phys. Rev. Lett. 102, 127005 (2009).
Bean, C. P. Magnetization of high-field superconductors. Rev. Mod. Phys. 36, 31 (1964).
Norris, W. T. Calculation of hysteresis losses in hard superconductors carrying ac: isolated conductors and edges of thin sheets. J. Phys. D: Appl. Phys. 3, 489–507 (1970).
Yeshurun, Y. & Malozemoff, A. P. Giant flux creep and irreversibility in an Y-Ba-Cu-O crystal: an alternative to the superconducting-glass model. Phys. Rev. Lett. 60, 2202 (1988).
Müller, K. A., Takashige, M. & Bednorz, J. G. Flux trapping and superconductive glass state in La2CuO4−y:Ba. Phys. Rev. Lett. 58, 1143 (1987).
Golovchanskiy, I. A., Pan, A. V., Shcherbakova, O. V. & Fedoseev, S. A. Rectifying differences in transport, dynamic, and quasi-equilibrium measurements of critical current density. J. Appl. Phys. 114, 163910 (2013).
Fal’ko, V. I., Volkov, A. F. & Lambert, C. Interplay between spin-relaxation and Andreev reflection in ferromagnetic wires with superconducting contacts. Phys. Rev. B 60, 15394 (1999).
Jedema, F. J., van Wees, B. J., Hoving, B. H., Filip, A. T. & Klapwijk, T. M. Spin-accumulation-induced resistance in mesoscopic ferromagnet-superconductor junctions. Phys. Rev. B 60, 16549 (1999).
Lee, W., Ji, R., Gosele, U. & Nielsch, K. Fast fabrication of long-range ordered porous alumina membranes by hard anodization. Nature Materials 5, 741–747 (2006).
Napolskii, K. S. et al. Tuning the microstructure and functional properties of metal nanowire arrays via deposition potential. Electrochim. Acta 56, 2378–2384 (2011).
Skryabina, O. V. et al. Josephson coupling across a long single-crystalline Cu nanowire. Appl. Phys. Lett. 110, 222605 (2017).
Acknowledgements
This work was supported by RFBR No. 19-02-00981 in the measurement part. M.Yu.K. and V.S.S. acknowledge the partial support by the Program of Competitive Growth of Kazan Federal University. V.S.S. and I.A.G. acknowledge the partial financial support of the Ministry of Education and Science of the Russian Federation in the framework of Increase Competitiveness Program of NUST MISiS (K3-2018-032).
Author information
Authors and Affiliations
Contributions
O.V.S. and V.S.S. suggested the idea of the experiment. O.V.S., I.A.G. and V.S.S. conceived the experiments. A.A.K. and K.S.N. grew the nanowires; O.V.S. and S.V.E., V.S.S. created the chip; O.V.S., S.N.K. and V.S.S. conducted the experiments. S.V.B. prepared the theoretical model, M.Yu.K., N.V.K., I.I.S., O.V.S., D.R. and V.S.S. interpreted the data; O.V.S., S.V.B. and K.S.N., V.S.S. wrote the manuscript. V.V.R., A.A.G. and D.R., V.S.S. revised the manuscript. All authors have read and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Skryabina, O.V., Kozlov, S.N., Egorov, S.V. et al. Anomalous magneto-resistance of Ni-nanowire/Nb hybrid system. Sci Rep 9, 14470 (2019). https://doi.org/10.1038/s41598-019-50966-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-50966-8
This article is cited by
-
Environment-induced overheating phenomena in Au-nanowire based Josephson junctions
Scientific Reports (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.