Abstract
Reanalysis data and a parametric typhoon model formula are often used to prepare wind and pressure fields for storm surge hindcasting. However, their optimum selection and usage have not been well established. To enhance the accuracy of wind and pressure fields, two hybrid methods were proposed by applying a parametric typhoon model of Mitsuta–Fujii’s formula, which is determined from the typhoon center to a certain radius of Rb, and then switching to the reanalysis data of ERA-Interim in the outer region through the interpolated transition bandwidth of Wb. In hybrid model I, Rb and Wb were fixed because the time-varying radius of the maximum wind speed was determined by the typhoon formula. In hybrid model II, these parameters were determined to minimize the mean difference between the reanalysis data and the fields obtained by typhoon formula in the transition band at each time step of the typhoon track. The hindcasting of eight significant typhoon events approaching Tokyo Bay was performed. This validated the proposed methods in comparison with the observed storm surge anomalies. Both models performed satisfactorily. Hybrid model II was found to be superior in terms of the balance of accuracy and preparation cost.
Similar content being viewed by others
Introduction
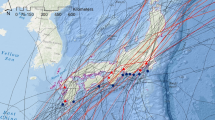
Tokyo Bay is a semi-enclosed coastal sea in the Greater Tokyo area, one of the largest city areas in the world, with a population of over 37 million (Fig. 1). Tokyo Bay area has been exposed to coastal hazards including storm surges1,2,3 and tsunamis4,5,6,7. In particular, storm surges are considered to be the most significant coastal disasters at the bay head where Tokyo Port and large commercial and residential areas are situated. According to a report by Chiba Prefecture Government8, the highest possible storm surge anomaly is projected to be 5.7 m at the bay head. The typhoon in the 6th year of the Taisho era (1917) caused one of the historical storm surges in Tokyo Bay, resulting in overflow of the coastal defense system and leading to extensive damage to properties and a loss of more than 1,300 lives1.
The accuracy of wind and atmospheric pressure data is important to storm surge hindcasting. A wide variety of parametric typhoon models have been developed to reproduce realistic atmospheric pressure and wind fields during typhoons or tropical cyclones, such as the Takahashi formula9, Fujita formula10, Jelesnianski formula11, Myers formula12, Mitsuta–Fujii formula13 (M–F), and Holland formula14. In these models, the maximum wind radius (rmax) that controls the maximum wind speed is a key parameter in determining the wind field, specifically the peak wind speed which could be estimated using several empirical formulae15,16,17. In contrast, the long-term reanalysis wind data obtained from data assimilation models has been widely used for storm surge hindcasting owing to its global availability and convenience. The data provided by the National Centers for Environmental Prediction (NCEP)18,19, European Center for Medium-Range Weather Forecasts (ECMWF)20,21, and Japanese Reanalysis (JRA)22,23 are the most commonly used reanalysis datasets. However, previous studies24,25,26,27,28 have shown that the wind speeds obtained near the typhoon center from the reanalysis data cannot accurately reproduce the observed wind fields. Thus, modifications are needed. Chao et al.26 proposed a framework to blend data from NCEP’s operational Global Forecast System (GFS) with that from a higher-resolution hurricane prediction model and successfully demonstrated an appropriately blended wind field for the typhoon-generated wind-wave prediction. However, the proposed method seems complex and impractical. Shao et al.27 presented two critical values as applicable ranges for ECMWF reanalysis wind data and Holland formula application for typhoon events that occurred in the South China Sea and East China Sea. With these two critical values, a weighting coefficient was given to combine two sets of wind data; however, the weighting coefficient was not clearly explained. Pan et al.28 proposed a similar superposition method and applied it to Typhoon Fanapi and Typhoon Meranti in 2010 by analyzing the cross-calibrated multi-platform (CCMP) reanalysis wind data. However, their method was not validated in storm surge hindcasting.
Thus, the objective of this study is to propose a practical method for creating accurate wind and atmospheric pressure fields by blending a reanalysis dataset and a parametric typhoon formula. The widely used ERA-Interim wind and atmospheric pressure reanalysis dataset (ERA-I) and M–F model were employed. Two hybrid methods for creating the fields were proposed; their performances were validated using the observed meteorological data provided by the Japan Meteorological Agency29 (JMA). Using the created atmospheric boundary data, hindcasting of two historical storm surges in Tokyo Bay was performed using the unstructured-grid Finite Volume Community Ocean Model30 (FVCOM 4.1), which has been applied to storm surge computations in several studies31,32,33,34,35,36,37.
The remainder of this paper is organized as follows. In Section 2, two hybrid methods are described and validated by comparison with the observed wind and atmospheric pressure fields, and the storm surge hindcasting is performed for the cases of Typhoon 8506 (the 6th typhoon in 1985) and Typhoon 1115 (the 15th typhoon in 2011) in Tokyo Bay, demonstrating the performance of the proposed hybrid methods. Section 3 presents the discussion and conclusions. Section 4 presents materials and methods.
Results
By introducing the radius of Rb and the transition bandwidth of Wb, a generalized hybrid method is proposed where the M–F model is applied in the 0 ≤ r ≤ Rb region and switching to ERA-I in the r ≥ Rb + Wb region (outer region of the transition band) while interpolating the two models in the transition band of Rb < r < Rb + Wb. In Section 2.2, this generalized idea (hybrid model II) is introduced with a method to determine the Rb and Wb parameter values. Before that, as a special case, hybrid model I is introduced in Section 2.1 by applying the M–F model in the region between the typhoon center (r = 0) and the applicable boundary, r = rmax, and switching to ERA-I in the region where r ≥ 2rmax. ERA-I and M–F model were smoothly interpolated in the transition band of rmax < r < 2rmax.
Hybrid model I
The direct method of determining the wind and atmospheric pressure field is given by:
where FB is the resultant wind velocity component in x or y direction, or the atmospheric pressure, FM−F and FERA are the wind velocity or atmospheric pressure from M–F model and ERA-I, respectively, r is the distance between the target location and typhoon center, and rmax is given by equation (6). Compared with the method of Shao et al.27, the proposed hybrid model can be easily used, and the weighting coefficient is explicitly explained.
Comparing the wind velocity distributions between the ERA-I and hybrid model I (see Supplementary Fig. S1), ERA-I and the M–F model dominated outside and inside the typhoon region, respectively, and the transition between these two models was continuous.
Comparisons between the computed (ERA-I, M–F model, and hybrid model I) and observed (JODC) wind speeds are shown in Supplementary Fig. S2. Their coefficients of determination are presented in Table 1. It can be seen that wind speeds computed by hybrid model I were more consistent with those of the observed (JODC) values during Typhoon 8506 and Typhoon 1115 than those computed by the M–F model or ERA-I.
Hybrid model II
The second hybrid model is based on the analysis of the difference between ERA-I and the M–F model. As shown in Section 2.1, the accuracy of the M–F model is higher than that of ERA-I around the typhoon center while the accuracy of ERA-I is higher than that of the M–F model away from the typhoon center. Thus, an optimum switching method between the M–F model in the central part and ERA-I in the outer typhoon region was obtained by interpolating the two data in the transition band at each time step for the typhoon track. At each time step, both the distance r = Rb from the typhoon center to the inner side of the transition band and the bandwidth Wb were investigated from r = 0 until r ≤ Lmax (Lmax is the maximum searching length) to minimize the mean value of the differences between ERA-I and M–F model across the computational grids within the transition band. For simplicity, a variable of the searching increment, Δr, was introduced where Rb = (m − 1)Δr (m is an integer number and 1 ≤ m ≤ n) and the maximum integer number of n was determined to satisfy (n − 1)Δr = Lmax − Wb (see Fig. 2). The formula for hybrid model II is given by:
Searching band areas in hybrid model II (the first parameter is the increase in the searching distance Δr, the second parameter is the maximum searching radius Lmax, the third parameter is the bandwidth Wb, which is the equal for all searching bands, and the fourth parameter is the distance from the typhoon center to the inner side of the transitional annulus band area Li (i = 1, 2, …, n). Rb equals Lm if the mth annulus is the band area within which the difference of ERA-I data and the M–F model is minimum. The searching begins from the first circle (black color) i = 1 with radius Wb, then the blue color annulus i = 2 with internal radius L2 = Δr, etc. The investigation stops when Ln + Wb = 1000 km. It is clear that in the proposed searching method, part of the neighboring band area is overlaps because the searching band area gradually expands with Δr).
The increment value of Δr was set as 5 km and the maximum searching length of Lmax was set as 1000 km, considering the balance between the accuracy and computational cost. Supplementary Fig. S3 shows the time series of the optimum Rb to rmax ratio for ten cases of Wb to obtain the optimum bandwidth. The ratios were always 0 when the distances from the typhoon center to the computational nodes were greater than 1000 km, e.g., in the period until 18:00 on June 28th. For all ten cases, the ratios were generally less than 2, which is consistent with the applicable radius, r, range for the M–F model (0 ≤ r ≅ rmax) as suggested by hybrid model I.
Comparisons between the computed winds (ERA-I, M–F model, and hybrid model II) and the JODC measured data during Typhoon 8506 and Typhoon 1115 are shown in Supplementary Fig. S4. Their coefficients of determination are summarized in Table 1, including the results of hybrid model I. According to Table 1, in some cases, such as Station Tokyo for Typhoon 8506 and Station Honmoku for Typhoon 1115, hybrid model I performed better than hybrid model II. In other cases, such as Station Honmoku for Typhoon 8506 and Station Tokyo for Typhoon 1115, hybrid model II was more accurate than hybrid model I. Thus, results show the accuracies of these two methods varied with cases and stations.
To further evaluate the performance of hybrid models I and II, eight selected typhoon cases were analyzed, and their corresponding root mean square errors (RMSE) were calculated by:
where Fhb−I,i is the wind velocity value or atmospheric pressure at the ith time step during a certain typhoon computed by hybrid model I, FJODC,i, is the corresponding measured wind speed or atmospheric pressure, and N is the total number of typhoon time steps. Supplementary Table S1 presents comparisons of the RMSE values among ERA-I and hybrid models I and II with different bandwidths. Compared with the original ERA-I RMSE values, both hybrid models were found to improve accuracy. However, the results from other cases showed that hybrid model II performed better with varying optimal bandwidths, compared with hybrid model I. Hybrid model I was considered a special case of hybrid model II where the bandwidth and band distance from the typhoon center were determined based on ERA-I and M–F model. Although the computational cost for hybrid model II was slightly higher, its performance was better and thus, would be a better choice for enhancing the accuracy of storm surge computation.
The hybrid model II concept was then applied to the atmospheric pressure fields, which is also vital in enhancing the storm surge computation accuracy. Comparisons of the time series of atmospheric pressures at Station Tokyo and Station Yokohama for Typhoon 8506 and Typhoon 1115 between ERA-I, Myers formula, hybrid model II, and observed data are shown in Supplementary Fig. S5. The blended atmospheric pressures obtained by hybrid model II were more consistent with those of the measured values. Thus, hybrid model II is confirmed to be superior.
Application to hindcast storm surge
To validate the performance of the proposed hybrid models for wind and atmospheric pressure fields, a hindcasting of storm surges in Tokyo Bay was performed using the finite volume community ocean model (FVCOM) forced by the wind and pressure data of ERA-I, M–F model with Myers formula, and the two hybrid models. To further consider the effect of possible water volume exchange between the ocean from a far place and the inner side of the bay, and also to reduce the boundary influence, a wide area was selected as the computational domain (20°N–60°N, 120°E–160°E) as shown in Fig. 3. A total of 34,255 computational nodes and 61,905 triangular elements were used.
Supplementary Table S2 summarizes the information on the storm surge observation stations38,39, and Fig. 1a shows the station locations in Tokyo Bay. To compare the performance of the hybrid wind data, the same set of parameters and boundary conditions were adopted except for the wind and atmospheric pressure data. The computation started with the still water condition with a mean sea level and zero velocities across the domain. For the wind data, ERA-I, M–F model, hybrid model I, and hybrid model II were used. For the atmospheric pressure data, Myers formula, ERA-I, and hybrid model II were applied.
Supplementary Fig. S6 shows the comparisons of the storm surge anomalies between the hindcasting results and observed data at six stations in Tokyo Bay for Typhoon 8506. Before the storm surge peaked at 5:00 on July 1st, 1985, the observed sea level anomalies at six stations were generally higher than the mean sea level (=0). ERA-I reproduced the observed tendency better than the M–F model with Myers formula. This indicates the significant influence of the atmospheric pressure fields on the reproducibility of sea level anomalies before the typhoon approach. However, ERA-I data substantially underpredicted the storm surge peak at all six stations, which implies the insufficient spatial resolution of ERA-I data to reproduce the surge peak. Comparing all the model results, hybrid model II (for both wind and atmospheric pressure fields) performed better in reproducing the storm surge anomalies during the typhoon approach, the surge peak, and the following oscillations induced by bay-scale resonance.
Supplementary Fig. S7 shows comparisons of the storm surge anomalies between the computed values using six models and the observed values for Typhoon 1115 at four stations in Tokyo Bay. M–F model could not reproduce the storm surge anomalies well before the peak, and the peak anomalies in Station Tokyo Harumi, Station Chiba, and Station Yokosuka were significantly lower than the observations. Similarly, ERA-I could not reproduce the peak anomalies at four stations. Among the six storm surge models, only hybrid model II (for both wind and atmospheric pressure fields) exhibited better results in reproducing storm surge anomalies.
To further evaluate the accuracy among the six models, the RMSE (defined by equation (3)) between the computed and observed values are presented in Table 2 for Typhoon 8506 and Typhoon 1115. The following are the periods of comparisons: from 6:00 on June 29th to 9:00 on July 2nd, 1985, for Typhoon 8506, and 3:00 on September 20th to 23:00 on September 23rd, 2011, for Typhoon 1115. According to Table 2, it can be concluded that the wind and atmospheric pressure fields obtained by hybrid model II should be used to hindcast storm surges.
Discussion and Conclusions
Parametric typhoon models and reanalysis datasets are widely used for storm surge simulation. However, only a few studies seek their optimum combination to enhance the accuracy of storm surge computation. In this study, two hybrid models were proposed for wind fields, where the M–F model was applied between the typhoon center (r = 0) and a certain radius (r = Rb), and switched to ERA-I when the radius is greater than Rb + Wb through the linearly interpolated transition band with the width of Wb. For hybrid model I, both Rb and Wb were fixed as the time-varying radius of rmax was determined by the M–F model at a distance from the typhoon center where the maximum wind speed occurred. Conversely, in hybrid model II, the optimum combination of Rb and Wb was determined to minimize the mean difference between the M–F model and ERA-I within the transition band. Thus, hybrid model II was considered to be the generalization of hybrid model I. The wind fields of the eight historical typhoon cases approaching Tokyo Bay were compared between ERA-I, the M–F model, hybrid model I, and hybrid model II. The accuracy of the typhoon wind fields calculated by ERA-I, the M–F model, hybrid model I, and hybrid model II were verified by comparison with the observed wind field provided by JODC. Results showed that while both hybrid models performed better than ERA-I and the M–F model, the accuracy of hybrid model II was higher than that of hybrid model I. The atmospheric pressure fields were also modified using hybrid model II.
Using FVCOM, hindcasting of storm surges in Tokyo Bay was performed by forcing six combinations of modeled wind and atmospheric pressure fields. The results showed that the modification of both atmospheric pressure and wind fields significantly improved the accuracy of the storm surge anomalies. Both proposed hybrid models performed better than the computations using only ERA-I or the M–F model. Hybrid model II can be easily tuned for each storm surge cases using only ERA-I and the M–F model data, which significantly improved the accuracy of storm surge hindcasting.
Forecasting the storm surge a short time period ahead of the typhoon’s arrival was out of the scope of this paper. However, the proposed method may be applied to the storm surge prediction under future climate conditions. The future atmospheric fields could be prepared using a general circulation model (GCM) with future climate scenarios, e.g., scenarios discussed in Intergovernmental Panel on Climate Change (IPCC) reports. Then, these atmospheric fields can be used in place of ERA-I reanalysis data for hybrid model I and II combining with parametric typhoon model.
Materials and Methods
Typhoon cases and observation stations
The locations of the meteorological observation stations in Tokyo Bay and its surrounding areas are shown in Fig. 1a. The stations recorded the tide levels, including the storm surge anomaly, and wind speed in a one-hour time interval. The detailed information, including the station names, longitudes, and latitudes, is summarized in Supplementary Tables S2 and S3.
Among historical typhoons and storm surges that occurred in Tokyo Bay between 1951 and 2017, 15 typhoon cases with large storm surge anomalies (greater than 0.8 m) were screened out and eight typhoons (see Fig. 1b) were selected as summarized in Supplementary Table S4.
Wind data analysis
Several reanalysis datasets are for wind and pressure fields, including the ERA-I, NCEP-DOE reanalysis II, and parametric typhoon models. A preliminary investigation was performed on the data consistency by a comparison with observed data from eight typhoon cases obtained in Section 4.1. ERA-I and the M–F model were used because both of them were more consistent with the measured data for the eight typhoon cases in Tokyo Bay during the preliminary study. Moreover, this method is applicable to any combination of reanalysis datasets and typhoon formulas.
ERA-Interim reanalysis data
ERA-Interim (ERA-I) is a global atmospheric reanalysis production provided by the European Center for Medium-Range Weather Forecasts (ECMWF), which started in 1979 and has since been continuously updated. In this study, ERA-I data of 6-hour interval wind speeds at a 10-m height from the mean sea level and the sea surface level atmospheric pressure were used. One-hour interval time series datasets for ERA-I were also created by interpolation. To obtain the most accurate ERA-I at the target stations, a 0.125° grid in the longitude and latitude was used.
Figure 4 shows a comparison of ERA-I and the measured wind data provided by Japan Oceanographic Data Center40 (JODC) at four stations during Typhoon 8506 and Typhoon 1115. When the center of Typhoon 8506 was far from Station Tokyo (1985/06/24/06:00-1985/07/01/00:00 and 1985/07/01/10:00-1985/07/03/06:00), Station Honmoku (1985/06/24/06:00-1985/06/30/18:00 and 1985/07/01/10:00-1985/07/07/00:00), and Station Shionomisaki (1985/06/24/06:00-1985/06/29/12:00 and 1985/07/02/12:00-1985/07/07/00:00), ERA-I was consistent with that of the measured JODC data. When the center of Typhoon 8506 approached Station Tokyo (1985/07/01/00:00-1985/07/01/10:00), Station Honmoku (1985/06/30/18:00-1985/07/ 01/10:00), and Station Shionomisaki (1985/07/01/00:00-1985/07/01/10:00), ERA-I was lower than that of the measured JODC data. For Typhoon 1115 and the other six typhoon cases, similar analyses were carried out.
With the typhoon center far from the stations, the wind speeds were fairly consistent with the observed data with the corresponding approaching and departing distances between the typhoon center and Station Tokyo, Station Honmoku, and Station Shionomisaki ranging from 3.94 rmax to 1.84 rmax (1985/7/1/0:00-1985/7/1/10:00), 3.09 rmax to 2.23 rmax (1985/6/30/18:00-1985/7/1/10:00), and 2.15 rmax to 2.44 rmax (1985/6/29/12:00-1985/7/1/12:00), respectively. With the aforementioned distances, large discrepancies between the observed data and ERA-I were noted.
After the ERA-I analysis for the eight typhoon events and the JODC observation data at eight stations, the applicable ranges for ERA-I are summarized in Table 3. The critical value, D1, is defined as the applicable distance limit from the typhoon center. It was proposed to identify the applicable range of ERA-I at a target location during the typhoon approach. ERA-I is applicable at a location when the distance from the typhoon center to the location is greater than D1. A similar explanation can be applied to D2, which is defined for the typhoon departure condition. The distances D1 and D2 consist of the applicable boundaries for ERA-I.
The first step in determining D1 and D2 values is the plotting of the time-series ERA-I data and JODC observed data at each station during the selected typhoon events. Instances with large discrepancies are then noted. The distance from the typhoon center to the station at the noted instance is finally calculated as the D1 value for this typhoon. The distance of D2 is similarly determined under the departing condition. As shown in Table 3, different stations experienced the whole processes of the eight selected typhoon events. Statistics at the eight stations under different typhoon events resulted in different D1 values. It can be seen that D1 and D2 values are approximately 2 rmax. Hence, to simplify the following analysis, D1 and D2 are set as 2 rmax.
Parametric typhoon model description
The Myers formula based on the exponential distribution of the atmospheric pressure field is given by:
where P(r) is the pressure at a radial distance r from the typhoon center, Pc (hPa) is the typhoon central pressure, P0 (=1013.25 hPa) is the ambient or environmental pressure, r is the distance from the computational mesh node to the typhoon center, and rmax (km) is the maximum wind speed radius.
After reviewing similar studies17,41, the M–F model was selected to compute the wind field as presented in equation (5) and the estimated pressure by equation (4) was applied to the M–F model.
Uw is the total wind vector, Uw1 is the moving component, Uw2 is the wind vector induced by the rotating component, P(r) is the pressure field calculated by Myers formula, C1 and C2 are dimensionless coefficients ranging from 0.6 to 0.75, f is the Coriolis parameter, r is the distance from the typhoon center, ρa is the atmospheric density, and VT is the typhoon forward speed obtained from the best track data29 provided by the JMA including the typhoon center location and central pressure. The time-varying radius of the maximum wind speed, rmax, was determined as a function of central pressure, Pc, following the empirical formula17:
Applying this model to the eight typhoon cases, the estimated wind speeds were compared with the observed data for Typhoon 8506 and Typhoon 1115 cases as shown in Supplementary Fig. S2. In general, for large wind speeds, the estimated values were consistent with that of the measured data. Following Section 4.2.1, the applicable boundary distances of D3 and D4 were determined for the M–F model from the typhoon center to the target location when the typhoon is respectively approaching and departing, as shown in Table 3 (D3 and D4 are approximately equal to rmax). Thus, M–F model is applicable in the area between the typhoon center (r = 0) and the boundary (r = rmax).
References
Miyazaki, M. Study of Storm Surge. Seizando Publishing, ISBN4-425-51181-6, 134pp (in Japanese) (2003).
Hoshino, S., Esteban, M., Mikami, T. & Takagi, H. Estimation of increase in storm surge damage due to climate change and sea level rise in the Greater Tokyo area. Natural Hazards 80(1), 539–565 (2016).
Kawai, H., Hashimoto, N. & Matsuura, K. Improvement of stochastic typhoon model for the purpose of simulating typhoons and storm surges under global warming. Proc. 30th Int. Conf. Coast. Eng. (ICCE2006) 2, 1838–1850 (2006).
Hatori, T. Behaviors of the 1703 Genroku Kanto, the 1854 Ansei Tokai and other tsunamis along the coast of the Tokyo Bay to Uraga Strait. Rekishijisin, 21, 37–45 (in Japanese) (2006).
Yasuda, T. & Hiraishi, T. Experimental study of tsunami inundation in coastal urban area. Proc. 14th Int. Offshore and Polar Eng. Conf. 740–746 (2004).
Sasaki, J. et al. Behavior of the 2011 Tohoku earthquake tsunami and resultant damage in Tokyo Bay. Coast. Eng. J. 54(1), 1250012 (2012).
Wiyono, R. U. A., Sasaki, J. & Suzuki, T. Numerical assessment of the 2011 Tohoku earthquake tsunami in ports of Tokyo Bay with the effectiveness of floodgates. J. Coastal Res. SI65, 844–849 (2013).
Chiba Prefecture Government Report, https://www.pref.chiba.lg.jp/kakan/shinsui/takashio.html (2018).
Takahashi, K. Distribution of pressure and wind in a typhoon. J. Meteorological Soc. Japan 17(2), 417–421 (1939).
Fujita, T. Pressure distribution within typhoon. Geophysical Magazine 23(4), 437–451 (1952).
Jelesnianski, C. P. A numerical calculation of storm surges induced by a tropical storm impinging on a continental shelf. Monthly Weather Review 93(6), 343–358 (1965).
Myers, V. A. Maximum hurricane winds. Bulletin of the American Meteorological Soc. 38(4), 227–228 (1957).
Mitsuta, Y. & Fujii, T. Analysis and synthesis of typhoon wind pattern over Japan. Bulletin of the Disaster Prevention Res. Inst. Kyoto Univ. 37(4), 169–185 (1987).
Holland, G. J. An analytic model of the wind and pressure profiles in Hurricanes. Monthly Weather Review 108(8), 1212–1218 (1980).
Graham, H. E. & Nunn, D. E. Meteorological Conditions Pertinent to Standard Project Hurricane. Atlantic and Gulf Coasts of United States, Weather Bureau, U.S. Department of Commerce, Washington, D.C (1959).
Knaff, J. A. et al. Statistical tropical cyclone wind radii prediction using climatology and persistence. Weather Forecast 22(4), 781–791 (2007).
Kato, F. Study of storm surge risk assessment. National Institute for Land and Infrastructure Management Reports (2005).
Kistler, R. et al. The NCEP–NCAR 50-year reanalysis: monthly means CD-ROM and documentation. Bulletin of the American Meteorological Soc. 82, 247–267 (2001).
Saha, S. et al. The NCEP climate forecast system reanalysis. Bulletin of the American Meteorological Soc. 91, 1015–1057 (2010).
Uppala, S. M. et al. The ERA-40 re-analysis. Quarterly J. Royal Meteorological Soc. 131(612), 2961–3012 (2005).
Kiss, P. & Jánosi, I. M. Comprehensive empirical analysis of ERA-40 surface wind speed distribution over Europe. Energy Conversion and Management 49(8), 2142–2151 (2008).
Onogi, K. et al. The JRA-25 Reanalysis. J. Meteorological Soc. Japan 85, 369–432 (2007).
Kobayashi, C. & Iwasaki, T. Brewer-Dobson circulation diagnosed from JRA-55. J. Geophys. Res.: Atmospheres 121(4), 1493–1510 (2016).
Cavaleri, L. & Sclavo, M. The calibration of wind and wave model data in the Mediterranean Sea. Coast. Eng. 53(7), 613–627 (2006).
Signell, R. P. et al. Assessment of wind quality for oceanographic modeling in semi-enclosed basins. J. Marine Systems 53(1–4), 217–233 (2005).
Chao, Y. Y., Alves, J. H. G. M. & Tolman, H. L. An operational system for predicting hurricane-generated wind waves in the North Atlantic Ocean. Weather and Forecasting 20, 652–671 (2005).
Shao, Z. X., Liang, B. C., Li, H. J., Wu, G. X. & Wu, Z. H. Blended wind fields for wave modeling of tropical cyclones in the South China Sea and East China Sea. Applied Ocean Res. 71, 20–33 (2018).
Pan, Y., Chen, Y. P., Li, J. X. & Ding, X. L. Improvement of wind field hindcasts for tropical cyclones. Water Sci. and Eng. 9(1), 58–66 (2016).
Japan Meteorological Agency, https://www.jma.go.jp/jma/indexe.html.
Chen, C., Liu, H. & Beardsley, R. C. An unstructured, finite-volume, three-dimensional primitive equation ocean model application to coastal ocean and estuaries. J. Atmospheric and Oceanic Technology 20(1), 159–186 (2003).
Chen, C. et al. Extratropical storm inundation testbed: Intermodel comparisons in Scituate, Massachusetts. J. Geophys. Res.: Oceans 118(10), 1–20 (2013).
Sun, Y. F. et al. Impact of current-wave interaction on storm surge simulation: A case study for Hurricane Bob. J. Geophys. Res.: Oceans 118(5), 2685–2701 (2013).
Yoon, J. J., Shim, J. S., Park, K. S. & Lee, J. C. Numerical experiments of storm winds, surges, and waves on the southern coast of Korea during Typhoon Sanba: the role of revising wind force. Natural Hazards and Earth Sys. Sci. 14(12), 3279–3295 (2014).
Rego, J. & Li, C. Storm surge propagation in Galveston Bay during Hurricane Ike. J. Marine Systems 82(4), 265–279 (2010).
Aoki, A. & Isobe, A. Application of finite volume coastal ocean model to hindcasting the wind-induced sea level variation in Fukuoka Bay. J. Oceanography 63(2), 333–339 (2007).
Ma, Z., Han, G. & Young, B. Modelling the response of Placentia Bay to hurricanes Igor and Leslie. Ocean Modelling 112, 112–124 (2017).
Ding, Y. & Ding, L. A numerical simulation of extratropical storm surge and hydrodynamic response in the Bohai Sea. Discrete Dynamics in Nat. and Soc. 2014, 282085 (2014).
Bureau of Port and Harbor, Tokyo Metropolitan Government, http://www.kouwan.metro.tokyo.jp/.
Japan Coast Guard, http://www1.kaiho.mlit.go.jp/.
JODC. JODC Dataset. (Available, http://www.godac.jamstec.go.jp/bismal/j/JODC_J-DOSS (2013).
Tajima, Y., Gunasekara, K. H., Shimozono, T. & Cruz, E. C. Study on locally varying inundation characteristics induced by super Typhoon Haiyan. Part 1: Dynamic behavior of storm surge and waves around San Pedro Bay. Coast. Eng. J. 58(1), 1640002 (2016).
Acknowledgements
The first author thanks for the financial support by China Scholarship Council (Grant No.: 201606270197). The measured wind data were provided by Japan Oceanographic Data Center (JODC). Typhoon best track data and the measured atmospheric pressure data were provided by Japan Meteorological Agency (JMA). The measured storm surge anomaly data were provided by JMA, Bureau of Port and Harbor, Tokyo Metropolitan Government, and Japan Coast Guard. The authors appreciate Dr. Changsheng Chen at University of Massachusetts Dartmouth and his team for providing the FVCOM model. The computation was carried out using the computer resource offered under the category of General Projects by Research Institute for Information Technology, Kyushu University.
Author information
Authors and Affiliations
Contributions
F.L. and J.S. designed the study. F.L. performed the data analysis and the numerical computation. F.L. wrote the main manuscript, including the figures and tables. J.S. reviewed and revised the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, F., Sasaki, J. Hybrid methods combining atmospheric reanalysis data and a parametric typhoon model to hindcast storm surges in Tokyo Bay. Sci Rep 9, 12222 (2019). https://doi.org/10.1038/s41598-019-48728-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-48728-7
This article is cited by
-
A novel deep learning approach for typhoon-induced storm surge modeling through efficient emulation of wind and pressure fields
Scientific Reports (2023)
-
Numerical assessment of coastal multihazard vulnerability in Tokyo Bay
Natural Hazards (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.