Introduction

It is well known that surfaces of most icy bodies in the outer Solar System and interstellar space consist mainly of water and are regularly bombarded with energetic particles and photons. This irradiation triggers a spectrum of physicochemical processes inside solid phase1,2,3,4: the formation of primary products (H, OH, H2, and О); their fast recombination or leaving from the initial position with subsequent diffusion inside ice; reactions between them, with H2O or impurities; appearance of secondary products (HO2, HO3, H2O2, O2, O3); trapping of primary and secondary products by the ice matrix and their accumulation; and the flow of products into gas phase. The characteristics of these processes greatly depend on the characteristics of irradiation, ice type, its thickness, temperature, additives, and others. The end products such as H2O2, O2, O3, etc., both in solid and gas phase are of considerable interest for astrophysics as they are all oxidizing agents and may provide a source of chemical energy as a fuel for extraterrestrial life5.

The established detection of H2O2 on Europa’s surface6 and the discussed existence or absence of H2O2 on Enceladus, Ganymede, and Callisto7 stimulated extensive laboratory studies of the mechanisms of formation and measurement of the parameters of producing concentrations of this component in high-purity H2O ice and H2O ice with different additives irradiated by energetic particles8,9,10,11,12,13,14. In particular, it was shown that, as compared to H2O ice, the presence of О2 greatly increases the production of H2O2 and other products (HO2, HO3, and O3), especially at relatively high irradiation temperatures of 80–120 К. At the same time, except for a few works, significantly less attention was paid to investigation of H2O2 production by VUV photons. In particular, Gerakines et al.15 and Schriver et al.16 reported about H2O2 formation in H2O ice at 10 K irradiated by microwave discharge hydrogen flow lamps. Yabushita et al.17 found out H2O2 presence in H2O ice after its irradiation by 157 nm photons at 90 K. Shi et al.18 measured H2O2 in porous H2O + O2 ice irradiated by 193 nm photons at 40–78 K. Thus, many details of H2O2 production by VUV photons, the temperature dependence in the first place, are still understood poorly.

This work reports the first results of laboratory measurements of H2O2 production inside thin H2O and H2O:O2 ice samples irradiated by 121.6 nm photons in the temperature range of 20–140 K. We discuss possible implications of the obtained results at the surface of astrophysical water ice bodies and inside the particles of Noctilucent Clouds in the Earth’s atmosphere.

Noctilucent Clouds

There exists at least one analog of such water icy bodies regularly irradiated by VUV photons in the Earth’s atmosphere. Each summer at polar and middle latitudes, one can observe the highest atmospheric clouds called Noctilucent Clouds (NLCs). They appear in mesopause region (altitudes range of 80–90 km) at the temperatures of 120–150 K19,20,21. Since the clouds discovery22, there were many discussions about their nature (see reviews by Gadsden & Schröder19 and by Thomas20). Only recently, the infrared spectra of clouds showed23 that NLCs consisted mainly of water ice. Thus, it is not doubt now that clouds form by condensation of water vapour and can influence on gas-phase chemistry of this region due to water vapour is its key parameter.

In the conditions of daytime mesopause, water vapour is subjected to intensive solar VUV radiation (121.6 nm, so called the Lyman–α line) and the reaction H2O + hv → H + OH provides the main chemical source of the family of odd hydrogen (HOx: H, OH, and HO2)24. In turn, the reactions with participation of HOx components (O3 + H → O2 + OH, O + OH → O2 + H, O + HO2 → O2 + OH, and O3 + OH → O2 + HO2) remove the components of the odd oxygen family (Ox: O(1D), O(3P), and O3). Therefore, the appearance of NLCs is expected to reduce the concentrations of water vapour and HOx and to increase Ox. However, rocket measurements of the concentration of atomic oxygen made during several campaigns demonstrated unpredicted O depletion around NLCs25. A possible explanation of the revealed effect was proposed by Murray and Plane26 who noticed that there also occurs photolysis of H2O molecules inside NLCs particles. The photoproducts (H and OH) may release into gas phase and additional source of HOx leads to increase of Ox removal. In the work by Kulikov et al.27 this hypothesis was verified by laboratory measurements of the photodesorption rate from thin water ice samples irradiated by 121.6 nm photons in the temperature range of 120–150 K. It was found that most photoproducts did not leave the solid phase and tended to recombine in water molecules back. Basing on the results of ice irradiation by energetic particles at relatively high temperatures of 80–120 К8,9,10,11,12,13,14, we can assume that H2O2 is the principal photoproduct that may accumulate in NLCs.

Note that the experimental evidence of H2O2 concentration increase in the presence of clouds was obtained long ago. Arnold and Krankowsky28 presented results of several rocket mass-spectrometer measurements of H2O2+ ions above Andoya (Northern Norway, 69○ N) taken in different seasons. The model estimates of the concentration of those ions formed as a result of the H2O2 + O2+ → H2O2+ + O2 reaction agreed well with the results of measurements made in different seasons, except summer. The authors conjectured that the discrepancy was caused by the increased H2O2 concentration in the summer time. Later measurements29 revealed positively charged clusters containing H2O2 in the presence of NLCs particles. The researchers arrived at the conclusion that for such clusters to be formed, the concentration of H2O2 must be much higher than the expected level.

Experimental Results

Hydrogen peroxide was found by detecting the IR absorption band of 2850–2860 cm−1 appeared in FTIR spectra of H2O and H2O:O2 ice samples as the result of their irradiation by calibrated source of 121.6 nm photons at high vacuum conditions. For more details please see Methods.

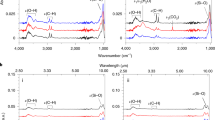
The results of 1 hour irradiation of thin ice samples by Lyman-α photons at the photon flux intensity Iα = 5·1014 photons/(cm2·s) are presented in Fig. 1. One can see that, in the case of H2O ice (Fig. 1a), H2O2 is formed at temperature of irradiation (Tir) ≤ 60 К, and the temperature rise from 20 to 60 К results in a monotonic decrease of the integrated area of the 2850–2860 cm−1 band (\({S}_{{H}_{2}{O}_{2}}\)). At these temperatures, H2O2 peak position is at 2860 cm−1. The experiments with thin water ice samples doped with O2 give more interesting results (see Fig. 1b). First, H2O2 is formed in the entire studied temperature range of 20–140 К. Second, the temperature dependence of \({S}_{{H}_{2}{O}_{2}}\) is nonmonotonic, so that it attains its maximum (~0.38 ± 0.057) cm−1 at about 100 К. Third, typical values of \({S}_{{H}_{2}{O}_{2}}\) at 20–60 K are essentially higher that the maximum recorded in experiments with H2O ice at 20 К (~0.085 ± 0.013) cm−1. Forth, H2O2 peak position lays at 2850 cm−1 in the range of 20–100 K and shifts to 2852–2854 cm−1 at the temperatures 120–140 K. Note also, in both cases, there are no new features at 1039, 1142, and 1259 cm−1 (see Fig. 1c) which can be attributed to O3, HO2, and HO3 correspondingly11,12.

Figure 1
figure 1

(a–c) Difference spectra (before and after irradiation) of H2O ice and H2O:O2 ice after 60 min of Lyman–α irradiation (Iα = 5 · 1014 photons/(cm2•s)) at different temperatures showing the temperature dependence of the appearance of H2O2 band near 2850–2860 cm−1 and the absent of new features at 1039, 1142, and 1259 cm−1 which can be attributed to O3, HO2, and HO3 correspondingly. Spectra above 20 K have been shifted vertically by an amount (shown in parentheses) to facilitate the display of the entire series. (d) Integrated area of the 2850–2860 cm-1 band as a function of temperature irradiation corresponding to (a,b).

Full size image

Figure 2a shows the examples of \({S}_{{H}_{2}{O}_{2}}\) dependencies on irradiation time (VUV fluence) at Iα = 5·1014 photons/(cm2·s). Note firstly, the present results are in a qualitative agreement with H2O2 temporal evolution obtained in earlier laboratory studies of the formation of this component in H2O ice irradiated by energetic particles8,11,14 and photons15. The temporal evolution of \({S}_{{H}_{2}{O}_{2}}\) can be divided into two parts: growth stage when \({S}_{{H}_{2}{O}_{2}}\) increases monotonically, and saturation stage. In both cases, \({S}_{{H}_{2}{O}_{2}}\) is saturated after ~1 hour irradiation. In the case of H2O ice, the growth stage continues for ~20–30 min and can be described by a quadratic function of irradiation time (VUV fluence). This corresponds to the results of irradiation of H2O ice by Lyman-α photons at 10 K obtained by Gerakines et al.15. In the case of H2O:O2 ice, the growth stage continues for ~10 min and can be described by a linear function of irradiation time (VUV fluence). Such behavior of \({S}_{{H}_{2}{O}_{2}}\) in the case of H2O:O2 ice was found at other photon flux intensities. It means that, in the case of H2O:O2 ice, the H2O2 production during the growth stage can be fit successfully to a (pseudo) first-order reaction. We can conclude that the rate of H2O2 production is proportional to Iα and can determine the H2O2 photochemical quantum yield (\({\gamma }_{{H}_{2}{O}_{2}}\), the number of molecules of H2O2 generated per a Lyman-α photon absorbed by ice) as a function of Tir following, for example, Cooper et al.12 and Hand and Carlson14. For this, we carried out special experiments with H2O:O2 ice at lowIα = 3·1013 photons/(cm2·s) at which the growth stage continued more than 100 min. The Fig. 2b shows the examples of \({S}_{{H}_{2}{O}_{2}}\) dependencies on irradiation time (fluence) at different Tir with corresponding linear fits whose values of slope are presented on Fig. 2c.

Figure 2
figure 2

(a,b) Examples of integrated area of the 2850–2860 cm-1 band (color circles with bars) as a function of irradiation time (fluence) at Iα = 5·1014 photons/(cm2·s) (a) and at Iα = 3 · 1013 photons/(cm2·s) (b). Dashed lines in (a) indicate linear and quadratic fits. Color lines in (b) are linear fits. (c) Slope of the fit as a function of temperature irradiation corresponding to (b).

Full size image

Estimation of H2O2 Column Density and H2O2 Photochemical Quantum Yield

All known studies of H2O2 production after irradiation of different ices7,14,30,31,32,33,34,35,36 used the values of \({A}_{{H}_{2}{O}_{2}}\) (the strength of the 2850–2860 cm−1 band absorption) from two sources8,10. Moore & Hudson8 measured \({A}_{{H}_{2}{O}_{2}}\) = 2.7·10−17 cm·molecule−1 and this value used for all temperatures. Loeffler et al.10 found out that \({A}_{{H}_{2}{O}_{2}}\) was 5.7·10−17 cm·molecule−1 at 20 K, 5.2·10−17 cm molecule−1 at 80 K, and 4.9·10−17 cm·molecule−1 at 110 K. Thus, for estimation of H2O2 column density (relative concentration) and H2O2 photochemical quantum yield from the results presented in Figs 1d and 2c, we applied both data sets (see Fig. 3a,b). In particular, Loeffler et al.8 data were interpolated into the temperature regions of 20–80 K and 80–110 K, and extrapolated to the temperature region of 110–140 K.

Figure 3
figure 3

(a) H2O2 column density and its relative concentration in pure H2O ice and in H2O:O2 ice as a function of temperature irradiation corresponding to Fig. 1d. (b) H2O2 photochemical quantum yield as a function of temperature irradiation corresponding to Fig. 2c. (c) H2O2 photochemical lifetime as a function of temperature irradiation corresponding to (a,b).

Full size image

One can see from Fig. 3a, that, in the case of H2O ice, the maximum of relative concentration H2O2/H2O at 20 K is ~2% at \({A}_{{H}_{2}{O}_{2}}\) from Moore & Hudson8 and ~1% at \({A}_{{H}_{2}{O}_{2}}\) from Loeffler et al.10. In the case of H2O:O2 ice, the maximum of H2O2/H2O at 100 K is ~9% at \({A}_{{H}_{2}{O}_{2}}\) from Moore & Hudson8 and ~4.5% at \({A}_{{H}_{2}{O}_{2}}\) from Loeffler et al.10. In that time, the maximum of \({\gamma }_{{H}_{2}{O}_{2}}\) is at 20 K (see Fig. 3b). Note also, that at the temperatures of possible NLCs existence (120–140 K), \({\gamma }_{{H}_{2}{O}_{2}}\) varies within ~(0.009–0.031) molecules/photon at \({A}_{{H}_{2}{O}_{2}}\) from Moore & Hudson8 and ~(0.0053–0.0175) molecules/photon at \({A}_{{H}_{2}{O}_{2}}\) from Loeffler et al.10.

Discussion and Conclusion

The possible mechanism of H2O2 formation during VUV irradiation of H2O ice was discussed by Gerakines et al.15 and pointed by Loeffler et al.10 in comparison with H2O2 formation by ions. This component is formed due to reaction OH + OH → H2O2. The quadratic character of \({S}_{{H}_{2}{O}_{2}}\) dependence on VUV fluence at the growth stage (see Fig. 2a) indicates a reaction of second order. It means that two photons are needed for appearance of one H2O2 molecule. These photons should produce two OH close to each other due to extremely low mobility of OH in water ice below 80 K37,38. The saturation of \({S}_{{H}_{2}{O}_{2}}\) after ~1 hour irradiation corresponds to the photochemical equilibrium when photoproduction is balanced by the photochemical sink due to the reactions H2O2 + hv → 2OH and H2O2 + OH → H2O + HO2.

In the case of H2O:O2 ice, the linear character of \({S}_{{H}_{2}{O}_{2}}\) dependence on VUV fluence at growth stage (see Fig. 2a) shows us that the mechanism of H2O2 formation differs from the previous case. Note, Loeffler et al.10 and Hand and Carlson14 found out the same behavior of \({S}_{{H}_{2}{O}_{2}}\) in H2O ice irradiated by high-energy ions and electrons correspondingly. It was proposed for explanation of this, in particular, that two OH could be produced in an ion track caused by an ion10. Evidently, this mechanism cannot be transferred on our situation. But, following Loeffler et al.10 and Hand and Carlson14, we can speculate that the rate of H2O2 formation in H2O:O2 ice irradiated by VUV photons is proportional to VUV intensity and the concentrations of H2O and O2. In other words, one photon, one H2O molecule and one O2 molecule are needed for appearance of one H2O2 molecule. On the other hand, O2 is impurity of H2O ice and typically two O2 molecules are separated from each other by a “paling” of H2O molecules. So, it is hard to imagine that these O2 molecules can participate in formation of one H2O2 molecule due to extremely low mobility of intermediates (such as OH and HO2) in water ice below 80 K as above mentioned. Thus, we can conclude as a first approximation that H2O2 photochemical quantum yield inside VUV irradiated H2O:O2 ice is proportional to the relative concentration of O2 (O2/H2O), when O2/H2O \(\ll \) 1.

Note, that, in the case of H2O:O2 ice, temperature dependences of H2O2 column density (\({N}_{{H}_{2}{O}_{2}}\)) and \({\gamma }_{{H}_{2}{O}_{2}}\) shown in Fig. 3a,b allow to estimate the H2O2 photochemical lifetime (\({\tau }_{{H}_{2}{O}_{2}}\)) with the use of the photochemical equilibrium condition \({\tau }_{{H}_{2}{O}_{2}}\cdot {N}_{{H}_{2}{O}_{2}}={\gamma }_{{H}_{2}{O}_{2}}\cdot {I}_{\alpha }\). On can see from Fig. 3c that \({\tau }_{{H}_{2}{O}_{2}}\) has a maximum at 60–80 K and the temperature rise from 20 to 60 К results in an essential increase of \({\tau }_{{H}_{2}{O}_{2}}\). For explanation of this, we should take into account that H2O2 photochemical sink is due to the reactions (1) H2O2 + hv → 2OH and (2) H2O2 + OH → H2O + HO2. So, \({\tau }_{{H}_{2}{O}_{2}}={({R}_{1}+{R}_{2}\cdot OH)}^{-1}\), where R1,2 are the corresponding reaction rate coefficients. Note, Loeffler et al.39 measured the loss of H2O2 in H2O:H2O2 at temperatures between 21 and 145 K initiated by UV photons (193 nm). They obtained that the temperature dependences of H2O2 photodestruction cross section (\({\sigma }_{{H}_{2}{O}_{2}}\)) had a minimum at ~70 K which value was in ~5 and ~3 times more than \({\sigma }_{{H}_{2}{O}_{2}}\) at 20 K and 145 K correspondingly. Thus, following Loeffler et al.39, we can speculate that nonmonotonic temperature dependency of \({\sigma }_{{H}_{2}{O}_{2}}\) shown in Fig. 3c is caused by strong and nontrivial temperature dependency of cross section of H2O2 photodestruction by irradiation of our lamp which defines the value of R1. More detailed analysis of obtained results is out of the scopes of this short paper.

Thus, at the relatively high temperatures >60 К, H2O2 is photoproduced in H2O:O2 ice only. The estimated values of \({\gamma }_{{H}_{2}{O}_{2}}\) inside such ice can be used for assessing the impact of Lyman-α photons on water ice and its contribution to H2O2 production in different applications.

In astrophysics, VUV irradiation competes with energetic particles bombardment3,40. Moore and Hudson8 and Cooper et al.12 measured H2O2 production inside H2O:O2 = 6:1 ice mixtures irradiated with 0.8 MeV protons. It was found that G-value (defined as the number of H2O2 molecules created per unit of absorbed energy) varied in the range of 0.2–0.4 molecules/100 eV at 50–100 K, that is close to G-value of Lyman-α photons at 50–100 K obtained in our paper. Thus, contribution of Lyman-α photons to H2O2 production is defined by the ratio between energy fluxes of photons (EFph) and energetic particles (EFep). In the case of EFph~EFep, photons produce approximately the same amount of H2O2 inside ice as particles. At that, as it was noted by Gerakines et al.40, the penetration depth for Lyman-α photons (~45 nm41) in water ice is essentially less, than for protons which depends on its energy (for example, 1–2 μm for 0.1 MeV protons10 and 22 μm for 1 MeV protons42). So, one would expect the high relative H2O2 concentration in the top few tens of nm caused by Lyman-α photons. It means that H2O2 production by VUV photons can be important at EFph/EFep ≥ 10−2.

In the mesopause region of the Earth’s atmosphere, typically EFph \(\gg \) EFep. But, at this moment, there is no information about containing of O2 inside water ice of Noctilucent Clouds. It is well-known that NLCs are formed as a result of gas-kinetic collision of H2O molecules with the surface of mesospheric aerosols, including adsorption and desorption properties. It is, generally, a relatively slow process, with the characteristic time (2–20 hours) depending on temperature43. In the real conditions of a summer mesopause, H2O concentration in gas phase is more than 4 orders of magnitude less than the concentration of O2 in ground (triplet) state and less than daytime concentration of O2 in singlet state ((2–4)·109 cm−3 at 80–85 km44). The molecules of O2 in ground and excited states, like those of H2O, continually bombard the surface of the forming particles of clouds, adsorb on their surface and can be trapped inside the ice matrix as the NCL particles are being covered by new ice layers. This suggests that a small part of O2 molecules from gas phase may be uptaken by the forming matrix of the cloud. It is certainly hard to believe that the relative concentration of O2 inside NCL particles (\({O}_{2}^{NLC}\)) can be equal to 10% at such high temperatures. Nevertheless, we can estimate minimum of \({O}_{2}^{NLC}\) at which photoproduced H2O2 concentration would be comparable with the gas-phase concentration of this component.

Let us assume that \({\gamma }_{{H}_{2}{O}_{2}}^{NLC}\) is unknown H2O2 photochemical quantum yield in NCLs particles. Then the rate of H2O2 production per 1 cm3 at a certain altitude is defined by \({P}_{{H}_{2}{O}_{2}}={\gamma }_{{H}_{2}{O}_{2}}^{NLC}\cdot {S}_{Mie}\cdot {I}_{\alpha }\), where Iα is the local flux intensity of Lyman-α photons and SMie is the Mie absorption cross-section of NLCs, SMie ≈ SNLC/4, where SNLC is the NLC surface density. According to the data of the long-term (1998–2005) measurements with the ALOMAR RMR-lidar in Northern Norway (69○ N, 16○ E), at the altitudes of 81–86 km SNLC varies within the (3–6)·10−8 cm2/cm3 range45. Taking into consideration that at these heights in the conditions of average solar activity Iα~3 · 1011 photons/(cm2·s)24, we obtain \({P}_{{H}_{2}{O}_{2}}\) ~ (2.25–4.5)·103·\({\gamma }_{{H}_{2}{O}_{2}}^{NLC}\) molecules/(cm3·s). In the real conditions of the mesopause, the NLCs particles are also irradiated by UV solar photons, which leads to H2O2 photodissociation in solid phase with the efficiency close to this process in gas phase39. For the considered range of altitudes of 81–86 km, the photodissociation constant of H2O2 in gas phase \({R}_{{H}_{2}{O}_{2}}\) is ~1.5 10−4 s−1. Thus, the equilibrium concentration of H2O2 that may be accumulated in cloud particles irradiated by Lyman-α photons is \({P}_{{H}_{2}{O}_{2}}/{R}_{{H}_{2}{O}_{2}}\,\) = (1.5–3)·107·\({\gamma }_{{H}_{2}{O}_{2}}^{NLC}\) cm−3. Gumbel et al.25 reported the maximum of SNLC~10−7 cm2/cm3, which gives the estimate for the maximum values of \({P}_{{H}_{2}{O}_{2}}\) and equilibrium concentration of H2O2 to be 7.5 · 103·\({\gamma }_{{H}_{2}{O}_{2}}^{NLC}\) molecules/(cm3·s) and 5 · 107·\({\gamma }_{{H}_{2}{O}_{2}}^{NLC}\) cm−3, correspondingly. Under the conditions of NLCs existence, typical value of gas-phase concentration of H2O2 is ~2 · 105 cm−3 at 81 km and decreases with increasing height down to the values less than 104 cm−3 at 86 km26. Thus, the minimum of \({\gamma }_{{H}_{2}{O}_{2}}^{NLC}\), at which photoproduced H2O2 concentration is equal to 104 cm−3, corresponds to 2 · 10−4 molecules/photon. Following our above conclusions, H2O2 photochemical quantum yield inside H2O:O2 ice is proportional to the relative concentration of O2. Taking into consideration the measured values of \({\gamma }_{{H}_{2}{O}_{2}}\) inside H2O:O2 = 9:1 ice at the temperatures of 120–140 K, we estimate that the minimum of \({\gamma }_{{H}_{2}{O}_{2}}^{NLC}\) = 2·10−4 molecules/photon corresponds to \({O}_{2}^{NLC}\) ~ (0.065–0.22)% (i.e. the absolute concentration of O2 in NLCs ~(1.4–4.9)·105 cm−3) at \({A}_{{H}_{2}{O}_{2}}\) from Moore & Hudson8 and ~(0.11–0.38)% (the absolute concentration ~(2.5–8.3)·105 cm−3) at \({A}_{{H}_{2}{O}_{2}}\) from Loeffler et al.10. Note, that the estimated values of the O2 absolute concentration in NLCs are several orders of magnitude less than typical gas-phase concentrations of this component in ground and singlet states at the altitudes of 81–86 km.

To conclude, we have demonstrated for the first time that, if NLCs particles contain ≥0.1% O2, the physicochemical processes occurring in them may remarkably affect the chemical composition of the mesopause region. On the one hand, it may be a possible explanation of the results of early rocket mass-spectrometer measurements28,29 indicating increased H2O2 concentration in the clouds. On the other hand, H2O2, product of its UV photodissociation (OH), H2O, O2 and other impurities (for example, CO2) can participate in subsequent reactions producing more complex chemical compounds inside NLCs as it takes place, for example, in the bulk of supercooled water particles46. We hope that this research stimulates further experimental and theoretical investigations of the chemical composition of cloud particles. Note also that the obtained results are interesting for astrophysical applications, for example, for assessing the contribution of VUV irradiation to H2O2 production in the outer Solar System and interstellar space depending on temperature.

Methods

Apparatus

The experimental set-up was the same as we used under laboratory measurements of the photodesorption rate from water ice. As described by Kulikov et al.27, the apparatus consisted of a Fourier Transform Infrared Spectrometer (Bruker IFS 66 v)), a closed-cycle He refrigerator (Leybold ROK 10–300), a gas preparation and inlet system (further briefly GPIS), and a high-vacuum chamber with a volume of about 1000 cm3 pumped continuously by a turbomolecular pump system (Leybold-Heraeus) securing a high vacuum in the chamber down to the 10−8 mbar range. Inside the chamber, at the cold end of the cryostat there was a vertically mounted aluminium mirror (2.5 × 4 cm in size) as a substrate whose temperature was precisely regulated by a temperature controller (Lake Shore, model 340). The mirror temperature could be selected in the 10–300 K range. The GPIS was equipped with baratrons and needle valves. The upper part of the high vacuum chamber had two ports, one of which was equipped with a MgF2 (5 mm thick) input window for a VUV lamp. The second port had a KBr window for the IR beam of the FTIR spectrometer. The input for the VUV lamp made an angle of incidence of ~450 to the mirror surface and, according to the estimates of the manufacturer, MgF2 transmitted about 60% of the quantum flux at the wavelength of 121.6 nm. As a VUV source (Lyman–α) we used a resonance hydrogen lamp (Opthos Instruments) containing a mixture of 10% H2 and 90% Ar excited by a microwave generator (Opthos Instruments, model MPG-4M) with a frequency of 2450 MHz. The lamp intensity was determined by the power supplied by the microwave generator (about the lamp calibration see below). The FTIR spectrometer was placed on rails allowing precise positioning of the instrument with respect to the cryostat with the sample. This was important for achieving a good overlap of the areas of the light spots from both, infrared (from spectrometer light source) and vacuum ultraviolet irradiation (from VUV lamp) of the ice film sample on the substrate. The operation of the FTIR spectrometer was PC controlled by means of software (OPUS) that permitted scanning spectra over a wide range (from 6000 to 500 cm−1) and analyzing the obtained spectra. The spectra were recorded with a spectral resolution of 0.2–2 cm−1 in the RAIRS mode (reflection absorption infrared spectroscopy) where the IR beam passes through the sample twice.

Experimental procedures

The experimental procedures were almost the same as we used under laboratory measurements of the photodesorption rate from water ice. As described by Kulikov et al.27, each experiment with a particular sample of ice was conducted in two stages. At the first stage, two background spectra with different resolution were recorded at a mirror temperature of 20 K and at a temperature of subsequent irradiation (Tir). At that time, H2O or H2O + O2 gas was got ready in GPIS. We used the oxygen (Air Liquide 5.5) with purity better than 99.9995 Vol% and triply distilled water with resistivity better than 107 ohm cm, additionally degassed by freeze/thaw cycles in vacuum conditions. As described in our previous study27, then, an ice film was prepared by depositing H2O or H2O + O2 vapour onto the mirror at 20 K. The deposition speed and sample thickness were controlled by a needle valve and internal baratron of GPIS and by tracking the evolution of absorption bands in the FTIR spectra. More specifically, a sample was prepared by successive slow depositions of small vapour portion which were accompanied by the integrated area measurements of the water ice 3275 cm−1 band (\({S}_{{H}_{2}O}\)). At the end of each sample deposition, we tried to rich the value of \({S}_{{H}_{2}O}\,\) = 31 ± 1 cm−1 which was equivalent to H2O column density \({N}_{{H}_{2}O}\,\) = (1.55 ± 0.05)·1017 molecules/cm2 at the strength of band absorption \({A}_{{H}_{2}O}\,\) = 2·10−16 cm/molecule taken from Allamandola et al.47. Here we applied the widely used14,30,47 approach to estimate a column density of absorbing molecules: \({N}_{{H}_{2}O}={S}_{{H}_{2}O}/{A}_{{H}_{2}O}\). In the case of H2O ice, the indicated values of \({N}_{{H}_{2}O}\) responded to thickness sample of 50 ± 1.6 nm at ice density of 0.93 g/cm3. In the case of H2O:O2 ice, we might expect increasing thickness of samples not more than 10%. Thus, the thicknesses of H2O and H2O:O2 ice samples were comparable with the attenuation depth (~45 nm41) of 10.2 eV photons in water ice and close to typical radii of NLC particles48. After the sample preparation, the mirror temperature was set at Tir (in the 20–140 K range) and several IR spectra of unirradiated ice were recorded. At Tir = 120 K and above, the IR spectra showed crystalline features of all ice samples that was in accordance with composition of NLCs49. Note also, Bartels-Rausch et al.50 discussed recently the simulations of disorder on pure ice at different temperatures below melting point (Tm) and showed that, at the temperatures 10 K below Tm, disorder affected the first molecular layer of ice only. In current study, the samples consisted of more than 100 layers of water and the highest temperature in our experiments (140 K) was about 20 K below than characteristic Tm of water ice in our vacuum chamber. Thus, we can conclude that interface processes could not influence essentially on the studied processes inside ice samples.

As described in our previous study27, at the second stage, the vacuum ultraviolet lamp was switched on and the ice films were exposed to VUV radiation with intensity set by microwave generator. After each photolysis period, IR spectra of the irradiated ice films were recorded. For improving the signal-to-noise ratio we used the spectral resolution of 2 cm−1 and a large amount of scans (2000). Hydrogen peroxide was found by detecting the IR absorption band of 2850–2860 cm−1 in difference spectra (before and after irradiation). The band was exuded by subtracting the baseline from the spectrum in manner described, for example, in Hand & Carlson14. Values of H2O2 column densities were determined as \({N}_{{H}_{2}{O}_{2}}={S}_{{H}_{2}{O}_{2}}/{A}_{{H}_{2}{O}_{2}}\), where \({S}_{{H}_{2}{O}_{2}}\) was the integrated area of the 2850–2860 cm−1 band, \({A}_{{H}_{2}{O}_{2}}\) was the strength of the band absorption.

Calibration of the hydrogen discharge lamp

The calibration was carried out in the same manner as it was described by Kulikov et al.27. Before an experiment with specific H2O or H2O + O2 ice sample, we performed series of measurements of the absolute magnitude of the flux of Lyman-α photons that reach the ice sample at different adjustments of the microwave generator power. The widely used “ozone method”16,51 was applied for the procedure. The intensity of the lamp was determined by measuring the O2 → O3 conversion rate in a VUV photolyzed sample of solid O2 at 16 K. The ozone formation as a function of photolysis time was monitored with the FTIR spectrometer via the O3 absorption band at about 1040 cm−1. More specifically, for finding the VUV intensity at the mirror for a specific generator output power (GOP) we made successive measurements of the integrated area of the 1040 cm−1 absorption band (\({S}_{{O}_{3}}\)) as a function of irradiation time (see Fig. 2 in Kulikov et al.27). After that, the lamp intensity at this GOP was determined as \({I}_{\alpha }=d{S}_{{O}_{3}}/dt\cdot {(Y\cdot {A}_{{O}_{3}})}^{-1}\), where the derivative \(d{S}_{{O}_{3}}/dt\) was found by the linear part of the function \({S}_{{O}_{3}}(t)\), Y was the quantum yield for the formation of O3 from O2, and \({A}_{{O}_{3}}\) was the strength of the band absorption. The value of \(Y\cdot {A}_{{O}_{3}}\) was adopted from Cottin et al.52 and was equal to 8.4 · 10−18 cm·photon−1. We obtained that, depending on GOP varied within the range of 4–120 W, the photon flux intensity varied within the range 5 · 1012–1015 photons/(cm2•s). The stability of lamp intensity at the fixed GOP was checked by means of photodiode SXUV300 (International Radiation Detectors).