Abstract
Direct calorimetric measurements of a solid state passive switchable radiator for spacecraft thermal control have been performed in a simulated space environment. Dynamic emissivity control is provided by the thermochromic phase change in a multilayer VO2 thin film based resonant absorber. The measured radiated power difference between 300 K and 373 K was 480 W/m2 corresponding to a 7× difference in radiative cooling power. We present theoretical and experimental radiator values for both normal and hemispherical as well the optical properties of VO2 as determined via infrared spectroscopic ellipsometry.
Similar content being viewed by others
Introduction
Thermal control is essential for the proper operation and longevity of space borne assets. Spacecraft thermal management systems often cope with the transient nature of thermal environments in space, such as orbital eclipses, seasonal changes in solar intensity and sun angle variation, as well as dynamic internal thermal loads (e.g. electronics, sensors, propulsion, etc.). Radiative heat transfer through a spacecraft’s thermal radiator into deep space is the sole mode of heat rejection. The thermal radiator alone is not capable of regulating the temperature but often requires supplemental heaters, heat pipes and control systems to maintain the spacecraft temperature within a desirable range1,2. An alternative approach is to dynamically control the emittance of the radiator via macro and micro mechanical louvers3,4,5,6; however, these louvers are sizable for small satellites and are susceptible to mechanical wear. Therefore, the development of cost effective, lightweight, high reliability thermal control systems (TCS) are critical for successful spacecraft missions.
Ideally, a more direct approach would modulate the emissivity of the radiator itself such that when the spacecraft temperature is lower than ideal, the emissivity is decreased to reduce radiative heat loss and when the spacecraft temperature is higher than ideal, the emissivity is increased to radiate the unnecessary heat, thus maintaining a stable spacecraft temperature. To address this matter, electrochromic7 and thermochromic8,9 variable emittance coatings have been proposed to provide efficient thermal control for spacecraft. For this work, we focus on phase change thermochromics because they do not require the use of electrical stimulus. Thin-film-based, passive TCS have been reported based on phase change materials such as chalcogenides, perovskite oxides, and vanadium dioxide (VO2), which can provide temperature-switchable emissivity. Chalcogenide phase change materials such as Ge2Sb2Te5 (GST) have been proposed to provide highly switchable emissivity10,11,12. The non-volatile switching nature between the amorphous GST and crystalline GST is ideal from a thermal control standpoint but the high temperature (913 K) necessary for crystallization requires additional power and control systems. Phase-changing materials such as perovskites and VO2 are more favorable because their structural phase transitions occur at lower temperatures offering the possibility of a totally passive self-regulating thermal control system. Switchable emittance was demonstrated using the perovskite oxide La0.7Ca0.2Sr0.1MnO313,14,15; however, the width of the temperature range during the phase transition was too large (~200 K) to be an effective thermal control device.
VO2 is a thermochromic material well suited for TCS applications because of its dramatic change in optical properties near its phase change temperature, TC ~340 K16,17,18. When T < TC, VO2 exhibits a monoclinic phase structure with an insulating state that is transparent to infrared (IR) radiation. When T > TC, the VO2 phase switches to a tetragonal phase with metallic properties and becomes IR reflecting19,20. Upon the transition to the metallic state (T > TC), its reflectance in the mid-infrared (IR) wavelength region increases and, accordingly, its emittance (ε) decreases (Δε <0) making VO2 suitable for smart window applications21,22,23,24. However, the opposite behavior (increase in emittance with increasing temperature) is required in order for VO2 to be used for spacecraft thermal control applications.
There have been many efforts aimed at achieving a positive, large emissivity change in VO2-based TCS. However, while the majority of these efforts have been theoretical studies, only a handful of experimental demonstrations have been reported. For example, it was reported that a VO2 film grown on an aluminum substrate showed a positive emittance change of Δε = 0.22, which is too low to be an efficient TCS6. Recently, Wu et al. provided a theoretical analysis of thermal homeostasis based on VO2 coated on a textured Si substrate for a switchable thermal emitter with a 10x emission change between the insulating and metallic states25. Hendaoui et al. reported a sandwich-like multilayer structure that consists of an 850 nm-thick SiO2 film sandwiched between a front VO2 thin film (30 nm) and a back infrared reflecting Au layer (350 nm) deposited on a quartz substrate. This multilayer structure provides a near normal emissivity change of Δε = 0.49 between 300 K and 373 K19,26. However, this multilayer structure can be degraded due to the environment in outer space. For example, the VO2 front layer will slowly oxidize into highly-valent V2O5 when exposed to atomic oxygen flux conditions, which greatly deteriorates its thermochromic properties9.
In this work, we provide direct measurements of emitted power from a VO2-based Fabry-Perot thin film radiator in a simulated space environment. This is in stark contrast to the bulk of previous published results which infer radiator performance from near normal optical measurements, rather than performing a direct power measurement27. In addition, most previously published work report near normal reflectance values which result in normal emittance values only28. These results are inadequate because they do not take into account the angular dependence of emissivity. Because of this, hemispherical emittance is required to fully and accurately describe the system. Rather than calculating the hemispherical emittance from reflectance measurements, which is difficult due to the number of angles, polarizations, and grazing incidences, we use a calorimetry method to directly measure the radiated power from which the emissivity can be extracted.
Multilayer Design
The multilayer radiator design consists of a BaF2 dielectric spacer placed between a VO2/Si front layer and a gold reflecting back layer. There are several advantages to this design. By growing the VO2 first, we can ensure deposition of high quality VO2 films by optimizing the high temperature growth conditions while minimizing any issues related to thermal expansion at the interfaces between the BaF2 and Au layers. In addition, the Si substrate, a good IR transparent material, can protect the multilayer coatings from the external environment including exposure to atomic oxygen flux leading to a longer device lifetime. Furthermore, the Au metal layer serves as the bottom contact with the spacecraft, resulting in better thermal contact to the surface of the spacecraft, which is essential for a good thermal radiator. Finally, BaF2 was chosen as a dielectric spacer because of its broadband transparency in the mid-infrared region up to 15 µm. Influence of the thickness of VO2 and BaF2 layers on the emittance variation and the temperature dependence of the emitted power were studied.
Figure 1 shows the multilayer structure (Si/VO2/BaF2/Au) with the insulating (metallic) VO2 layer at 300 K (373 K). When the temperature is below 340 K, the multilayer structure is highly reflective in the mid infrared due to the bottom Au layer, since the insulating VO2 and the BaF2 layers are highly transparent in the mid infrared region. However, when the temperature is increased above 340 K, the VO2 becomes metallic and serves as a top mirror for a Fabry-Perot resonant structure, generating an enhanced absorption (i.e., enhanced emissivity) in the mid-infrared region, thus increasing radiative cooling. In general, the resonance wavelength in this Fabry-Perot structure can be tuned by adjusting the spacer thickness. In addition, the amplitude and the width of the resonance can also be tuned by the top mirror thickness. Thus, the thickness of the BaF2 spacer and the VO2 top mirror were chosen to achieve a maximum interference effect in the mid-infrared region (8–12 µm) corresponding to the range of the maximum emission of blackbody radiation around 300–373 K, providing enhanced emissivity in the mid-infrared region.
Results and Discussion
Growth and characterization of VO2 films
It is well known that the synthesis of high quality stoichiometric VO2 films is challenging due to the multiple stoichiometries of vanadium oxides with multivalent vanadium cations (e.g., V2+, V3+, V4+ and V5+). Available reports on the electrical and optical switching properties (i.e., the resistivity change and infrared transmittance change) for VO2 films are not consistent. This inconsistency indicates that the film properties are greatly influenced by the film growth conditions. Figure 2(a) shows the θ/2θ XRD scan of a 40 nm thick VO2 film grown on a Si (100) substrate. The peaks at ~32.9° and 69.1° are attributed to the (200) and (400) planes of the Si substrate while the peaks at ~27.9° and ~57.5° correspond to the (011) and (022) planes of monoclinic VO2 (M) [JCPDF Card 76-0456] respectively. Thus, it is clear that the VO2 film is a highly (011) oriented crystalline and single phase VO2 structure. These stoichiometric VO2 films exhibit a significant drop in resistivity and IR transmittance as the temperature increases above the TC ~ 340 K. (Fig. 2b). It should be noted that a transition temperature of ~340 K is high for electronics cooling in small satellites; however, 340 K is still suitable for other subsystems such as solar arrays and reflectors. In cases where a lower transition temperature is required, it would be advantageous to dope or strain the VO2 thin film to reduce the transition temperature19,29.
Simulated reflectance of multilayer structures
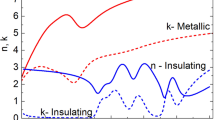
The optical constants (n and k) of an 80 nm VO2 and 1600 nm BaF2 were obtained from spectroscopic ellipsometry measurements by fitting the ellipsometric parameters (Ψ and Δ). Figure 3(a,b) show the optical constants of VO2 and BaF2, respectively, as a function of wavelength (2–25 µm) at 300 K and 373 K. The range of n and k values achieved in this work are similar to those previously reported by other groups for VO2 films grown on quartz (SiO2)6. Prior to device fabrication, the simulated reflectance spectra of the multilayer structure (Si/VO2/BaF2/Au) were generated as a function of VO2 layer thickness using the optical constants (n, k) data derived from ellipsometry measurements for both VO2 and BaF2 films. The BaF2 thickness used in these simulations is 1500 nm, which is determined to satisfy the Fabry-Perot condition of t = (mλRES) / (4n) at λRES = 10 µm, where m is an odd integer and n is the refractive index of BaF2. Figure 4 shows the variation of simulated reflectance spectra in the infrared wavelength region (2–25 µm) for these multilayer structures (Si/VO2/BaF2/Au) at two different temperatures (300 and 373 K). The VO2 layer thickness was adjusted because it is common for the optical constants to vary for thin films due to density, roughness, and phase purity. The structure consists of a 40 to 100 nm-thick VO2 layer, a 1500 nm-thick BaF2 layer and a 200 nm-thick Au reflecting layer on a Si substrate. As seen in Fig. 4(a), the reflectance spectra of multilayer structures at 300 K show slight variation in the 8–10 µm range as the VO2 film thickness changes from 40 to 100 nm. However, at 373 K, the variation of the reflectance spectra is clearly seen when the VO2 becomes metallic and is semi reflective in the infrared, which forms an interference filter with the BaF2 and underlying Au layer. The normal infrared emittance variation (Δε) of these multilayer structures between these two temperatures (300 K and 373 K) was calculated from these infrared reflectance spectra data using Equation (1) in Methods and summarized in Table 1. As the VO2 thickness decreases from 100 nm to 40 nm, the emissivity change of the multilayer structures increases from 0.31 to 0.52. Further decreasing the VO2 thickness below 30 nm decreases the Δε value. The largest change in normal emissivity of Δε ~ 0.52 was achieved from the multilayer structure with a 40 nm thick VO2 layer.
The effect of BaF2 thickness on the emissivity variation of the multilayer structures was also investigated using simulated reflectance spectra of the multilayer structures with BaF2 thickness of 600–1600 nm while the thickness of VO2 and Au was kept at 40 nm and 200 nm, respectively. As seen in Supplementary Fig. S1a, at 300 K as the BaF2 thickness increases from 600 to 1600 nm, the reflectance spectra of all samples are almost the same in the mid-infrared range (8–12 µm). However, at 373 K (Supplementary Fig. S1b), the reflectance spectra in the mid-infrared region gradually decreases with increasing BaF2 thickness. Thus, the overall Δε value increases slightly from 0.47 to 0.51 with the BaF2 thickness up to 1200 nm, where it saturates with a further increase to 1600 nm. (See Supplementary Table S1).
The hemispherical total emittance was numerically determined using Equation (2) in Methods. For a 60 nm VO2 film, the emittance at 300 K, εL, was calculated to be 0.15 and the emittance at 373 K, εH, was 0.54. It should be noted that the predicted change in total hemispherical emittance (Δεhemi) between 300 K and 373 K is 0.39, which is less than the normal emittance change (Δε = 0.45) (Table 1). The 60 nm sample was selected for hemispherical thermal power measurements as a compromise between performance and ease of fabrication.
Experimental reflectance of multilayer structures
Figure 5 shows the variation of measured reflectance spectra in the infrared wavelength region (2–25 µm) for these multilayer structures (Si/VO2/BaF2/Au) at two different temperatures (300 and 373 K). At 300 K, since the VO2 is insulating and both the VO2 and BaF2 layers are transparent in the mid-infrared range (Fig. 5a), the multilayer structure behaves like a simple metal mirror resulting in a low emittance of the structure. However, at 373 K, the VO2 layer becomes metallic and semi-transparent in the infrared (Fig. 5b), which creates an interference filter with the BaF2 spacer and underlying Au layer, resulting in high emittance (i.e., low reflectance) of the multilayer structure. The BaF2 films were measured via atomic force microscopy to have an RMS roughness of 40 nm corresponding to an optical flatness of λ/250 at 10 μm. The optical path error in our multilayer radiators due to BaF2 roughness results in an intensity error of less than 1%. As seen in Table 1, as the VO2 film thickness decreases from 100 nm to 40 nm, the emittance change (Δε) of the multilayer structures increases from 0.30 to 0.49 due to a decrease in reflectance spectra of the multilayer structures. In this work, the largest normal emittance change of ~0.49 was observed from the multilayer structure with a 40 nm thick VO2 film. These experimental results agree well with the simulation results (see Table 1).
Radiated thermal power measurements
As previously mentioned, hemispherical emittance is required to accurately calculate the radiated heat flux. Computation of hemispherical emittance from reflection data requires measurements at all angles of incidence, polarizations, and temperature. However, the indirect emittance measurements using reflectivity (R) data are experimentally prone to error and are difficult to achieve at near grazing angles. As an alternative, we performed calorimetric radiated power measurements as these are direct measurements of power radiated and do not require parameter retrieval from integration30,31.
Figure 6(a) shows a schematic illustration of the radiated thermal power measurement setup which is housed inside a vacuum chamber. Figure 6(b) shows the experimentally measured emitted power of the multilayer radiators as a function of temperature. As the device temperature increases, the emitted power increases as described by the Stefan-Boltzmann law, P = σεAT 4, where σ is the Stefan-Boltzmann constant, ε is the total emittance, A is the surface area, and T is the absolute surface temperature. The cold block was held at a temperature of 108 K and the radiated power of the device was determined from the amount of electrical power required to maintain the device at a given temperature. For comparison, the theoretical emitting powers, calculated from the simulated total hemispherical emittances of the multilayer radiator with the insulating and metallic VO2 phases, are also plotted in Fig. 6(b) (See Methods section). The hemispherical emittance values were extracted by fitting the measured experimental data, resulting in εL ~ 0.16 and εH ~ 0.51. The sharp increase in radiated power around T~ 340 K is due to the change in emissivity across the phase transition of VO2.
(a) A schematic illustration of radiated thermal power measurement setup in a vacuum chamber. (b) Radiated thermal power of a multilayer structure with a 60 nm thick VO2 layer. The direction of heating and cooling are indicated by arrows. The red and blue dashed lines represent the theoretical emitting power obtained from the simulated hemispherical emittance (ε) data with the insulating and metallic VO2, respectively.
The measured radiated power at 300 K and 373 K was 72 W/m2 and 552 W/m2, respectively. These results are consistent with a similar theoretical VO2-based design that took hemispherical emissivity into account27. Because the emitted power must be compared at two different temperatures, the measured emitted power is expected to differ by T4; therefore, it is helpful to measure the emitted power of the switchable radiator and to compare it with a radiator of fixed emissivity. This is accomplished by calculating the emitted power at 373 K using the experimentally determined hemispherical emissivity of 0.16. The predicted radiated power of a device without a phase transition is 175 W/m2 (for εL~ 0.16 at 373 K), whereas the experimentally measured radiated power for the multilayer device is 552 W/m2. A summary of the normal and hemispherical emissivities and emitted power are shown in Table 2. Overall, the experimental results agree well with our simulated results, to within ±~10% error. This dramatic change in radiated power enables a spacecraft radiator to expel more heat as its temperature rises above TC, resulting in a net cooling effect. As the spacecraft temperature decreases below TC, the emissivity of the radiator decreases, thereby emitting less power, resulting in lower heat loss of the spacecraft. Thus, this multilayer structure provides an efficient, self-regulating, and passive method of switching the radiated power emissivity between the insulating and metallic states of VO2 layers.
Conclusion
We have experimentally demonstrated a passive radiator for thermal control in a simulated space environement via direct calorimetric measurments. The VO2-based thermal radiator, which consists of a BaF2 dielectric spacer sandwiched between a VO2 layer and an Au reflecting layer, achieves passive and switchable thermal emissivity control based on the VO2 phase transition. When the VO2 layer is in an insulating state at T <340 K, the multilayer structure behaves like a simple infrared reflector, thereby minimizing radiative heat loss. However, when the VO2 layer switches to a metallic state at T >340 K, the multilayer structure behaves like a resonant absorber with high emissivity around the mid-infrared region (8–12 µm), thus providing a radiative cooling effect. A quantitative comparison between the emitted power using normal and hemispherical emissivity is presented. The radiator shows an excellent switchability of Δε ~0.47 comparable with previously published results using the normal emissivity values. However, using normal emissivity values leads to an overestimate of actual performance because it does not take into account the angular dependence of the multilayer radiator design. While the measured hemispherical emissivity change of the radiator was Δε ~ 0.35, the experimentally measured radiated power increases by more than a factor 7 with a net radiated power difference of 480 W/m2 between 300 K and 373 K. This large and reversible emissivity change makes this design well suited for spacecraft thermal control applications.
Methods
Radiator structure
The device design presented here consists of a three layer stack of VO2, dielectric BaF2 and Au films. First, VO2 films (40–100 nm) were deposited on (100) Si substrates (>1000 Ωcm) at T ~773 K in 12 mTorr of oxygen via pulsed laser deposition using a KrF excimer laser (LPX 300, 248 nm, pulse duration of 20 ns) from a stoichiometric VO2 target (ACI Alloys)29,32,33,34. BaF2 dielectric layers (1500 nm) were deposited on top of the VO2 layer by electron-beam evaporation. Finally, 200 nm thick Au layers were deposited on the BaF2 layer by electron-beam evaporation. Figure 1(a) shows a schematic illustration of the multilayer structure mounted upside down on the temperature controlled stage inside a FTIR [JASCO]. IR illumination is directed into the Si substrate.
Material characterization
X-ray diffraction (XRD) [Rigaku rotating anode X-ray generator with Cu Kα radiation] was used to characterize the crystal structure of the VO2 films. The electrical properties of VO2 films were measured by a four-point probe method at temperatures between 300 and 373 K. The optical reflectance spectra in the 2–25 µm wavelength range were measured at near normal incidence (10° AOI) at two temperatures (300 and 373 K) using an FTIR. The simulation studies were performed using the WVASE32 software (Woollam). The optical constants (refractive index n, extinction coefficient k) of the Au and Si substrates were obtained from the software database. The optical constants of VO2 and BaF2 layers were derived from ellipsometry measurements (IR-Vase, J. A. Woollam). A 200 nm thick Au film grown on a Si substrate was used as a reference. The roughness of the BaF2 films was measured by atomic force microscopy (Dimension Icon AFM, Bruker).
Emittance and radiated power calculation
The normal emittance of the multilayer devices was calculated from the reflectance spectra data by using Kirchhoff’s law, with the spectral emittance ελ, defined as ε(λ) =d1 – R(λ) for an opaque material, summed over the blackbody spectrum using the relation:
where R(λ, T) is the spectral reflectance at temperature T and J(λ, T) is the spectral blackbody radiation at temperature T given by Planck’s function for a given wavelength and temperature. The integral limits of λ1 and λ2 are 2 µm and 25 µm, respectively, as the blackbody radiation at room temperature is very weak beyond this range.
The hemispherical total emittance (εhemi) was calculated from the following equation35:
where ε(λ, θ, ɸ, T) is the directional spectral emissivity at temperature T and at an emission angle of θ and ɸ.
The total hemispherical emitted power was calculated from the following equation:
where σ is the Stefan-Boltzmann constant, εhemi is the hemispherical total emittance, A is the surface area, and T is the absolute surface temperature.
Direct radiated power measurements
The performance of the radiators was measured in a vacuum chamber by mounting a heater to the gold side of the radiator and placing a cold block ~1 cm from the surface of the radiator simulating the coldness of space (blackbody temperature ~ 108 K) as shown in Fig. 6a. The power delivered to the heater was varied while monitoring the sample temperature. Convective losses are assumed to be zero because the experiments were performed in vacuum (1 × 10−7 Torr). The conductive losses are small due to the high thermal isolation between the sample/heater and have been calibrated out of the test fixture. Therefore, the emitted power and change in emissivity can be determined directly from the power delivered to the heater.
References
Nagano, H., Nagasaka, Y. & Ohnishi, A. Simple deployable radiator with autonomous thermal control function. J. Thermophys. Heat Transfer 20, 856–864 (2006).
Goncharov, K. et al. 1500 W deployable radiator with loop heat pipe. In SAE Paper 012194 (2001).
Haddad, E. et al. Tunable emittance thin film coatings for thermal control. In: society of automotive engineers, Inc. Proceedings 2009-01, 2575–2587 (2009).
Beasley, M. A., Firebaugh, S. L., Edwards, R. L., Keeney, A. C. & Osiander, R. Design and packaging for a microelectromechanical thermal switch radiator. IEEE Inter Society Conference on Thermal Phenomena 4, 629–634 (2004).
Osiander, R., Firebaugh, S. L., Champion, J. L., Farrar, D. & Darrin, M. A. G. Microelectromechanical devices for satellite thermal control. IEEE Sensors Journal 4, 525–531 (2004).
Benkahoul, M. et al. Thermochromic VO2 film deposited on Al with tunable thermal emissivity for space applications. Sol. Energy Mater Sol. Cells 95, 3504–3508 (2011).
Demiryont, H. & Moorehead, D. Electrochromic emissivity modulator for spacecraft thermal management. Sol. Energy Mater Sol. Cells 93, 2075–2078 (2009).
Lang, F., Wang, H., Zhang, S., Liu, J. & Yan, H. Review on variable emissivity materials and devices based on smart chromism. Int. J. Thermophys. 39, 6 (2018).
Jiang, X. et al. Effects of atomic oxygen on the thermochromic characteristics of VO2 coating. J. Spacecraft & Rockets 43, 497–500 (2006).
Du, K. K. et al. Control over emissivity of zero-static-power thermal emitters based on phase-changing material GST. Light: Science & Applications 6, e16194 (2017).
Tittl, A. et al. A switchable mid-infrared plasmonic perfect absorber with multispectral thermal imaging capability. Adv. Mater. 27, 4597–4603 (2015).
Gholipour, B., Zhang, J., MacDonald, K. F., Hewak, D. W. & Zheludev, N. I. An all-optical, non-volatile, bidirectional, phase-change meta-switch. Adv. Mater. 25, 3050–3054 (2013).
Fan, D., Li, Q. & Dai, P. Temperature-dependent emissivity property in La0.7Sr0.3MnO3 films. Acta Astronaut. 121, 144–152 (2016).
Fan, D., Li, Q., Xuan, Y., Tan, H. & Fang, J. Temperature dependent infrared properties of Ca doped (La,Sr)MnO3 compositions with potential thermal control application. Appl. Therm. Eng. 51, 255–261 (2013).
Shen, X., Xu, G. & Shao, C. Influence of structure on infrared emissivity of lanthanum manganites. Physica B 405, 1090–1094 (2010).
Ramirez-Rincon, J. A. et al. Thermal hysteresis measurement of the VO2 dielectric function for its metal-insulator transition by visible-IR ellipsometry. J. Appl. Phys. 124, 195102 (2018).
Wang, S. et al. Recent progress in VO2 smart coatings: Strategies to improve the thermochromic properties. Prog. Mater. Sci. 81, 1–54 (2016).
Gao, Y. et al. Nanoceramic VO2 thermochromic smart glass: A review on progress in solution processing. Nano Energy 1, 221–246 (2012).
Hendaoui, A., Émond, N., Dorval, S., Chaker, M. & Haddad, E. VO2-based smart coatings with improved emittance-switching properties for an energy-efficient near room-temperature thermal control of spacecrafts. Solar Energy Materials & Solar Cells 117, 494–498 (2013).
Voti, R. L., Larciprete, M. C., Leahu, G., Sibilia, C. & Bertolotti, M. Optimization of thermochromic VO2 based structures with tunable thermal emissivity. J. Appl. Phys. 112, 034305 (2012).
Kats, M. A. et al. Vanadium Dioxide as a Natural Disordered Metamaterial: Perfect Thermal Emission and Large Broadband Negative Differential Thermal Emittance. Phys. Rev. X 3, 041004 (2013).
Kats, M. A. et al. Ultra-thin perfect absorber employing a tunable phase change material. Appl. Phys. Lett. 101, 221101 (2012).
Batista, C., Ribeiro, R. M. & Teixeira, V. Synthesis and characterization of VO2-based thermochromic thin films for energy-efficient windows. Nanoscale Res. Lett. 6, 301 (2011).
Guinneton, F., Sauques, L., Valmatette, J. C., Cros, F. & Gavarri, J. R. Optimized infrared switching properties in thermochromic vanadium dioxide thin films: role of deposition process and microstructure. Thin Solid Films 446, 287–295 (2004).
Wu, S.-H. et al. Thermal homeostasis using microstructured phase-change materials. Optica 4, 1390–1396 (2017).
Hendaoui, A., Émund, N., Chaker, M. & Haddad, E. Highly tunable –emittance radiator based on semiconductor-metal transition of VO2 thin films. Appl. Phys. Lett. 102, 061107 (2013).
Taylor, S., Yang, Y. & Wang, L. Vanadium dioxide based Fabry-Perot emitter for dynamic radiative cooling applications. J. Quant. Spectroscopy & Radiative Transfer 197, 76–83 (2017).
Wang, X., Cao, Y., Zhang, Y., Yan, L. & Li, Y. Fabrication of VO2-based multilayer structure with variable emittance. Appl. Surf. Sci. 344, 230–235 (2015).
Breckenfeld, E. et al. Strain Effects in Epitaxial VO2 Thin Films on Columnar Buffer-Layer TiO2/Al2O3 Virtual Substrates. ACS Appl. Mater. Interfaces 9, 1577–1584 (2017).
Musilova, V., Hanzelka, P., Kralik, T. & Srnka, A. Low temperature properties of materials used in cryogenics. Cryogenics 45, 529–36 (2005).
Herve, P. et al. Direct measurement of total emissivities at cryogenic temperatures: Application to satellite coatings. Cryogenics 48, 463–468 (2008).
Charipar, N. A., Kim, H., Mathews, S. A. & Piqué, A. Broadband terahertz generation using the semiconductor-metal transition in VO2. AIP Advances 6, 015113 (2016).
Kim, H., Charipar, N., Breckenfeld, E., Rosenberg, A. & Piqué, A. Active terahertz metamaterials based on the phase transition of VO2 thin films. Thin Solid Films 596, 45–50 (2015).
Kim, H., Charipar, N., Osofsky, M., Qadri, S. B. & Piqué, A. Optimization of the semiconductor-metal transition in VO2 epitaxial thin films as a function of oxygen growth pressure. Appl. Phys. Lett. 104, 081913 (2014).
Howell, J. R., Menguc, M. P. & Siegel, R. Thermal radiation heat transfer, 6th ed. 54–62 (CRC Press, 2016).
Acknowledgements
This work was funded by the Office of Naval Research (ONR) through the Naval Research Laboratory Basic Research Program.
Author information
Authors and Affiliations
Contributions
H.K., N.A.C. and K.C. designed the experiments. H.K., R.C.Y.A., N.A.C., D.W. and K.C. conducted experiments while H.K., K.M.C. and N.A.C. performed simulation work. H.K. wrote the manuscript while N.A.C. and A.P. contributed to analysis of the results and writing. All authors discussed results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kim, H., Cheung, K., Auyeung, R.C.Y. et al. VO2-based switchable radiator for spacecraft thermal control. Sci Rep 9, 11329 (2019). https://doi.org/10.1038/s41598-019-47572-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-47572-z
This article is cited by
-
Photonic structures in radiative cooling
Light: Science & Applications (2023)
-
Passive thermal control systems in spacecrafts
Journal of the Brazilian Society of Mechanical Sciences and Engineering (2023)
-
A novel design of a deployable CubeSat for material exposure missions in low earth orbit
CEAS Space Journal (2023)
-
Multimetal–VO2 Switchable Plasmonic Metasurface for High Contrast Optical Switching and Control at Short Wavelength Infrared Regime
Plasmonics (2023)
-
Infrared optical properties modulation of VO2 thin film fabricated by ultrafast pulsed laser deposition for thermochromic smart window applications
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.