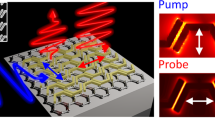
Abstract
Graphene’s giant nonlinear optical response along with its integrability has made it a vaunted material for on-chip photonics. Despite a multitude of studies confirming its strong nonlinearity, there is a lack of reports examining the fundamental processes that govern the response. Addressing this gap in knowledge we analyse the role of experimental parameters by systematically measuring the near-infrared spectral dependence, the sub-picosecond temporal evolution and pulse-width dependence of the effective Kerr coefficient (n2,eff) of graphene in hundreds of femtosecond regime. The spectral dependence measured using the Z-scan technique is corroborated by a density matrix quantum theory formulation to extract a n2,eff ∝ λ2 dependence. The temporal evolution obtained using the time-resolved Z-scan measurement shows the nonlinearity peaking at zero delay time and relaxing on a time-scale of carrier relaxation. The dependence of the n2,eff on pulse duration is obtained by expanding the input pulse using a prism-pair set-up. Our results provide an avenue for controllable tunability of the nonlinear response in graphene, which is limited in silicon photonics.
Similar content being viewed by others
Introduction
The Dirac band structure of graphene1,2 has endowed this atomically thin two-dimensional material with exceptional optical and transport properties. As a scale-invariant host of chiral carriers3, graphene exhibits a universal optical response in absorption, with a single sheet capable of absorbing ~2.3% of normally incident light. Its reduced dimensionality together with the peculiar Dirac type dynamics of the quasiparticles enable graphene to have a relatively strong nonlinear optical response in the presence of intense electromagnetic illuminations4,5. Intrigued by its potential applications in photonics and optoelectronics several theoretical and experimental studies of the nonlinear optical properties of graphene have been carried out3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22. Due to the centrosymmetric crystalline structure of graphene, even-order nonlinearities are forbidden, and the first nonlinear contribution is a third order effect. In particular, the Kerr type nonlinearity is dominantly attributable to the third order nonlinear interactions in graphene. The refractive index, n, considering the first nonlinear term is intensity dependent and is given by the expression n = n0 + n2I, where n0 is the linear refractive index, n2 is the Kerr coefficient, and I is incident intensity. This Kerr-type nonlinearity in graphene has been reported to be large, confirmed by studies characterising frequency mixing4,6,7, harmonic generation8, self-phase modulation9,10, and self-refraction5,11,12,13,14,15.
Several theoretical works have attempted to provide a cohesive theory for the third order nonlinearity in graphene, addressing the magnitude3,16,17,18 of the nonlinear refractive index (\({n}_{2}\)), the spectral3,4,16 and temporal19,20 dependence, and effects of Fermi energy modulation3,17,18,21,22. Although topological anomalies in graphene hinder the adaption of perturbation theory in the treatment of the optical response of graphene3,23, fortunately, over the optical wavelength range, nonlinear response coefficients can still describe interactions of photons. Perturbative treatment of the nonlinear optical response of graphene yields explicit expressions for the higher orders conductivity tensors. Throughout this work we refer to the third order frequency mixing conductivity as \({\sigma }^{(3)}({\omega }_{p},{\omega }_{q},{\omega }_{r})\) where \({\omega }_{p}\), \({\omega }_{q}\) and \({\omega }_{r}\) are the frequencies of the photons undergoing nonlinear interaction through the graphene monolayer. The conductivity is proportional to the Kerr coefficient through the third order susceptibility. The studies show large tunability in \({n}_{2}\) through Fermi level modulation. Other factors such as the spectral and temporal dependence have seen relatively less explicit theoretical discussion.
The experimental studies probing the Kerr-nonlinearity in graphene have shown variation in n2 spanning six order of magnitudes (10−12 to 10−7 cm2/W)4,5,11,14. A point of contention while comparing these results are the varying spectral and temporal properties of the excitation source, sample preparation techniques, and substrate material. The measurements are performed with the excitation wavelength ranging from the visible to the mid-infrared, while the pulse duration ranges from hundred femtoseconds to tens of picoseconds, under different sample preparation methods24. It has been recognised that the n2 depends on the wavelength, pulse duration and power in semiconductor systems25. Particularly in graphene, the n2 expected to become larger with longer wavelengths4. This trend has been observed and reported thereafter in the near15 and mid-infrared12 range, while spectral dependence in other regions remains experimentally unexplored. It has also been shown in graphene oxide, that the nonlinear parameters of the system change when excited with nanosecond and picosecond pulses26. The decrease of n2 with increasing incident intensity due to saturation effects has been observed and reported previously in several studies5,12,15,27. Raman studies have shown p-type doping occurs when chemical vapour deposition (CVD) graphene is transferred onto quartz24. Considering these factors, it is more apt to consider the measured nonlinear parameters in conjunction with the experimental conditions. This makes it imperative to understand the dependence of these factors to gain a fundamental understanding of the governing processes.
In this study we report a systematic analysis of the near-infrared spectral dependence, the sub-picosecond temporal evolution and pulse-width dependence of the effective Kerr coefficient (n2,eff) of graphene in hundreds of femtosecond regime using our pump-probe integrated Z-scan (PPZS) set-up. We refer to the nonlinear refractive index (n2) as n2,eff because we find that the nonlinearity in graphene comprises of the conventional Kerr-type nonlinearity and a component stemming from graphene’s unique structure. In addition to that, our set-up allowed for temporal measurements, unravelling the evolution of the nonlinearity in a pump-probe style measurement to reveal an ultrafast nonlinearity. Thus, this study provides a foundation for the development of predictable models imperative for device design, allowing for large controllable tunability of the nonlinear response of graphene.
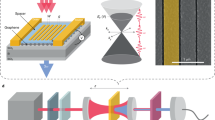
Originally introduced by Sheik-Bahae et al.28, the Z-scan technique proved to be an experimentally facile yet sensitive method to extract the phase and magnitude of the Kerr coefficient. The optically induced self-refraction is quantified by relating the phase modulation of the traversing beam to the transmittance in the far-field in Closed Aperture (CA) configuration, while the Open Aperture (OA) configuration captures the effect of absorption. This technique was modified by Wang et al.29 to extract the temporal evolution through the integration of a secondary time delayed beam to obtain the time-resolved Z-scan measurement. The PPZS set-up is schematically illustrated and further elucidated upon in the Methods and Materials section. The set-up can be operated in multiple modes of measurement. In the single-beam mode, the set-up is a standard Z-scan measurement. In dual-beam mode, with the addition of a lock-in amplifier, chopper and cross-polarisation filtering, the set-up can be used to perform a standard pump-probe measurement for the extraction of relaxation time constants. When used in conjunction with the Z-scan components, the dual-beam mode is used for the time-resolved Z-scan measurements.
Results and Discussion
Spectral-dependence
In order to verify the quality and monolayer nature of the samples, the CVD fabricated graphene on quartz (GoQ) samples (1 × 1 cm2) were characterised by Raman spectroscopy, shown in Fig. 1a. The G-band, 2D-band and D-band peaks appear at 1576 cm−1, 2661 cm−1 and 1328 cm−1, respectively. The relative intensities and widths of the G and 2D peaks confirm that the sample is single layer. We also perform a temporal correlation measurement on the sample, shown in Fig. 1b, to obtain a τ1 relaxation time constant of about ~113 fs. The methodologies and results are further discussed in the Methods and Materials section.
The spectral dependence of n2,eff is obtained in the single-beam Z-scan mode and is measured by scanning the 100 fs excitation source from 800 to 1050 nm with 50 nm increments. The range of the excitation is limited by tunability of the laser (690–1050 nm). Since the measurement is sensitive to the beam quality, the beam is characterised using a knife edge beam profiler for quality and stability over the period of the measurement. To ensure that the Z-scan modulation observed in the far-field is originating from graphene, a bare quartz substrate is measured at 900 nm at high on-axis irradiance to show no effect (see Supporting Information Fig. S5). The on-axis irradiance ranges from 1.5 to 5 GW/cm2, limited by the available power of the laser at each wavelength. A standard acquired Z-scan trace showing the OA, CA and Fit is shown in Fig. 2a. Our study focuses on the nonlinear refraction in graphene and not the nonlinear or saturable absorption. The OA trace is simply acquired for the normalisation of the CA trace for absorption effects, and presented for illustrative purposes to explain the quantum theory as presented shortly. The effects of saturation resulting in decrease of n2,eff with increasing irradiance is observed and shown at 950 nm in Fig. S6 in supporting information.
Spectral dependence of the n2,eff of graphene. (a) Standard Z-scan trace at 900 nm with the OA, CA and Fit shown. (b) Experimental data obtained using the Z-scan measurement spanning 800–1050 nm with 50 nm increments along with fit obtained from quantum theory. The experimental data matches the λ2 dependence predicted in theory. The uncertainties in γ1/2 are accounted for in our theoretical model by the shaded (yellow) region.
The cumulative results of the spectral dependence are presented in Fig. 2b along with the quantum theory based fit. A full set of Z-scan fits from which these results are compiled is also provided for reference (Fig. S7 in supporting information). The values for n2,eff in this regime are measured to be positive and range from 9.07 × 10−9 to 1.76 × 10−8 cm2/W in this excitation range which fits well with our quantum model with relaxation coefficients of γ1 ≈ γ2 ≈ 10 meV. The fitting parameters, γ1/2, are obtained from the time constants derived from the temporal cross-correlation measurement, shown in Fig. 1b. However, the pulse width of the pump and probes signals pose some uncertainties on the obtained decay constant of τ1 ~ 113 fs (see Methods and Materials) as the correlated pulses are of similar pulse durations. This uncertainty is accounted for in our theoretical model and is illustrated by the shaded (yellow) region in Fig. 2b. Shorter wavelengths are observed to have a n2,eff value that is lower as compared to longer wavelengths, with approximately the same on-axis irradiance. Our calculation suggests a quadratic dependence of n2,eff on λ which agrees with the experimental results. It is noted that n2,eff exhibits negligible dependence on the Fermi level for a low-doped graphene monolayer. In our case n2,eff is dominated by contributions from interband transitions and since the λ2 dependence is a direct consequence of the linear band diagram around the Dirac point, the most relevant transition occur at the zero detuning region where ω = 2|k|vF. Detuning is defined as \({{\rm{\Delta }}}_{k}=\hslash \omega -{ {\mathcal E} }_{cv}\), where ω is the frequency of the excitation photon and \({ {\mathcal E} }_{cv}\) is the energy of the transition, see Fig. 3a. The theoretical model employed in our theory uses semiconductor Bloch equations (SBEs) to describe the cooperative intra-interband dynamics of the population difference \({\mathscr{N}}(k,t)\) (between the valence and conduction bands) and the polarisation (coherence) \({\mathscr{P}}(k,t)\) for the Bloch state k. The phenomenological relaxation coefficients, γ1/2, account for the collective broadening effects for the population and coherence decay, respectively. The theoretical derivation is succinctly provided in the Methods and Materials section. Under our theory, the electromagnetic coupling for normal illumination is defined by \({{\rm{\Phi }}}_{k}=\frac{{\bf{E}}\cdot {\hat{\phi }}_{k}}{\hslash k}\), where E is the electric field and the unit vector \({\hat{\phi }}_{k}\) is defined as \({\hat{\phi }}_{k}=\hat{z}\times {\bf{k}}/k\), shown in Fig. 3a.
Carrier relaxation in graphene leading to Kerr-type nonlinearity. (a) Band structure of graphene showing the excitation pulse with energy ℏω, the zero detuning circle Δk = 0, and \({\hat{\phi }}_{k}\) is a vector in reciprocal space, (b) the evolution of the steady state population (\({{\mathscr{N}}}_{k}^{st}\)) and the equilibrium population (\({{\mathscr{N}}}_{k}^{eq}\)) difference upon intense illumination which disturbs the \({{\mathscr{N}}}_{k}^{eq}\) leading to the observation of a Kerr-type nonlinearity in graphene. At very intense illuminations population difference at the zero detuning circle becomes zero and absorption quenching takes place. The colours in the figures represent relative carrier population densities.
The nonlinear optical absorption has multiple origins namely bleaching effects culminating in saturation, and two photon absorption. Since the graphene sample used in our experiment is low-doped (i.e μ ≪ ℏω), absorption bleaching due to optically induced Pauli-blocking plays the leading role. This assumption is supported by observation of the absorption drops upon high optical irradiance, refer to the OA trace in Fig. 2a. Furthermore, since the Fermi energy level is small compared to the energy of the photons, it naturally follows that Pauli blocking around zero detuning region is widely demolished. Under high intensity illumination in a Kerr-type material, the charged carriers undergo ultrafast Rabi oscillations, much faster than their relaxation rate. As a consequence, the steady state population, \({{\mathscr{N}}}_{{\bf{k}}}^{st}\), is significantly modified by light, disturbing the distribution at equilibrium, \({{\mathscr{N}}}_{{\bf{k}}}^{eq}\). The origin of the Kerr-type nonlinearity is the optically induced change to the steady-state population difference. The relaxation dynamics as the population difference evolves is schematically shown in Fig. 3b. Before saturation takes place, the nonlinear contribution of the field to the population difference around the zero detuning region is a quadratic function of the field magnitude, \({{\mathscr{N}}}_{{\bf{k}}}^{st}-{{\mathscr{N}}}_{{\bf{k}}}^{eq}\approx -\frac{1}{{\gamma }_{1}{\gamma }_{2}}{{\mathscr{N}}}_{{\bf{k}}}^{eq}|{{\rm{\Phi }}}_{{\bf{k}}}{|}^{2}\). The induced nonlinear current oscillating at the frequency ω is then given by \({{\bf{J}}}_{NL}=\sum _{k}{\hat{\phi }}_{k}({{\mathscr{N}}}_{{\bf{k}}}^{st}-{{\mathscr{N}}}_{{\bf{k}}}^{eq}){ {\mathcal L} }_{{\bf{k}}}(\omega ){{\rm{\Phi }}}_{{\bf{k}}}\), where the Lorenztian \({ {\mathcal L} }_{{\bf{k}}}(\omega )\triangleq 1/({\gamma }_{2}+i{{\rm{\Delta }}}_{{\bf{k}}})\) accounts for the interband transitions. The nonlinear current JNL is the microscopic origin of the intensity dependence of the refractive index so that n2 ∝ |JNL|/|E|3. For a small enough γ2, the Kerr-type nonlinear induced current is given by:
where gs and gv are the spin and valley degeneracy factors, respectively, D = 1/4π2 is the density of states, and β~π is a dimensionless quantity that arises from angular integration around the Dirac cone. Due to low doping, \({{\mathscr{N}}}_{{\bf{k}}}^{eq}\approx 1\) over the zero detuning circle. Therefore, the frequency dependence of nonlinear current is dominated by the 1/k2 term appearing in Eq. 1. Over the Δk = 0 circle the Bloch wave-number k is linearly proportional to the frequency which in turn yields λ2 dependence of the Kerr nonlinear coefficient.
It is worth pointing out that the quadratic wavelength dependence of the Kerr coefficient is a direct consequence of the linear energy-momentum dispersion of the Dirac quasi-particles. The calculations outlined above can be effectively applied to all two-level condensed matter systems by appropriately replacing interband coupling into Eq. 1. However, exclusive to graphene is the 1/k dependence of the interband coupling Φk which results in the square wavelength dependence of the Kerr coefficient.
Temporal evolution
The temporal evolution of the nonlinearity is obtained using the dual-mode PPZS set-up. A single-beam (pump) Z-scan measurement is performed to locate the peak and valley positions of the sample. In order to locate the zero-delay position of the probe, the sample (GoQ) is placed at the peak position and the probe is scanned until a cross-correlation signal of the pump and probe pulses is obtained, shown in the inset of Fig. 4. The FWHM of the signal is 150 fs, which gives a pulse duration of 110 fs for the probe, considering a pulse duration of 102 fs for the pump. A similar scan is run at the valley position and both time-resolved data sets are used to extract the differential peak-valley transmittance, \({\rm{\Delta }}{T}_{pv}({t}_{d})=\pm [\frac{T({t}_{d},{Z}_{p})}{{T}_{OA}({t}_{d},{Z}_{p})}-\frac{T({t}_{d},{Z}_{v})}{{T}_{OA}({t}_{d},{Z}_{p})}]\), where Zp/v are the positions of the peak and valley, respectively, td is the probe delay, and TOA is the OA transmittance for normalisation. The sign of ΔTpv is given by the sign of Zp − Zv. The pump power used for this measurement was 200 mW, equating to an intensity of ~3.5 GW/cm2. The pump to probe power ratio was kept at 20:1. In general, the far-field aperture should only allow about 1% of light transmittance to isolate the effect of wave front distortion due to phase modulation, however, due to the weak signal of the probe the aperture is opened to allow 10% of transmittance with additional averaging at each acquisition point.
Pump-probe integrated Z-scan measurement. Time-resolved degenerate Z-scan measurement of graphene. Since ΔTpv is proportional to n2,eff, the plot follows the evolution of the induced phase modulation in graphene. The effect peaks at zero time delay and relaxes at longer time scales, showing some oscillatory behaviour as it relaxes. (Inset) Temporal cross correlation of pump and probe pulses at peak position.
The temporal evolution of the nonlinearity is shown in Fig. 4b. The effect peaks at zero probe delay and relaxes on the time-scale of τ1, while at longer time scales, τ2, ΔTpv shows no discernible variation. The symmetric shape of the figure leads us to believe that in this measurement we are simply observing the probe following the pump signals rather than unravelling the nonlinear phenomena hidden at shorter time scales. This is also supported by the fact that the pulse duration of the pump and probe is similar to the measured temporal cross-correlation extracted in Fig. 1b. Therefore, we can conclude that the relaxation dynamics contributing to the observation of the nonlinear refraction are simply too fast to be measured by our laser pulses in this manner. The variation of ΔTP−V or the induced phase shift ΔΦ seen in Fig. 4 relates to the Gaussian power distribution within the pump pulse which reaches its maximum value (i.e. ~3.5 GW/cm2) at the centre peak of the pulse. Therefore, according to \({n}_{2,eff}=\frac{\sqrt{2}{{\rm{\Delta }}{\rm{\Phi }}}_{0}}{{k}_{0}{I}_{0}{L}_{eff}}\) (see Methods and Materials), the n2,eff for the peak power is extracted to be 1.12 × 10−8 cm2/W. As the intensity decreases moving away from the peak, the n2,eff increasing in accordance with saturation. This measurement clearly shows that on the time scale greater than the heating and cooling times, the probe follows the pump and Kerr nonlinearity is tunable and controllable over this time scale. In this context, the heating and cooling times refers to the time-scale of carrier excitation to higher states and subsequent carrier relaxation to the ground state, respectively30. The modulation is understood through the relation n = n0 + Δn, where Δn = n2,effI, and the Δn parameter is modified as the n2,eff varies nonlinearly on the intensity prior to complete saturation5.
For the purposes of all-optical switching the on/off time of the nonlinearity is controlled by the pulse-duration and power of pulse. If the pulse-duration is longer than the effective relaxation times of the nonlinearity, then the evolution of the observed nonlinearity simply follows the Gaussian power distribution of the pulse. In this way through modulation of the Δn term, by changing the pulse properties, the switch can be controlled. However, there is saturation that takes place at relatively high intensities, leading to a deviation between the pump power within the pulse and the observed Δn.
Pulse-width dependence
It is well understood that the relative timescales of the excitation pulse and the system response times determine the induced dynamics in the system. To investigate the effects of pulse duration on nonlinear refraction, we stretch the ~100 fs pulse upto ~475 fs at 900 nm to observe the effects in the long pulse regime; longer than the duration of the nonlinearity or relaxation time, τ1. Pulse stretching is achieved using a dispersion-based prism-pair apparatus, where the pulse can be temporally expanded by varying the separation distance of prisms31. A schematic of the set-up is shown in Fig. S8 in supplementary information. In our set-up we use N-SF11 flint glass prisms. The maximum allowed pulse expansion is limited by the space on the optical table. The autocorrelation curves for the expanded pulses at which the Z-scan is performed are given in Fig. 5a and the results of the pulse-width dependence are provided in Fig. 5b. A set of Z-scan fits for the presented data is also provided in Fig. S9 in supporting information.
The results show a clear dependence of n2,eff on the excitation pulse duration, with n2,eff becoming larger with increasing pulse-width. This trend was theoretically speculated by Vermeulen et al.10 and shown here experimentally. The n2,eff ranges from 1.02 × 10−8 to 1.7 × 10−8 cm2/W in this pulse duration regime with a minimum between 200–300 fs. The decay constant τ1~113 fs measured in Fig. 1b falls near the beginning of the data set. However, doping can modify the decay constant values with p- and n-doping making the time constants long and shorter, respectively32. This data trend coincides with previously reported Z-scan studies on graphene performed with picosecond excitation where the n2,eff is larger than what is reported in the femtosecond regime. In addition to this, a similar comparative analysis performed on carbon disulphide (CS2), reference material used for calibration of Z-scan measurements, revealed a similar dependence of the n2,eff on pulse duration33. In a recent publication10, this pulse-width dependence of n2,eff is theoretically derived for a regime when the effective decay constant is larger than the pulse duration in Z-scan measurements. The interplay of relative carrier heating and cooling times is said to induce a nonlinear response that may not originate only from the conventional electronic Kerr-type nonlinearity but also from what they refer to as saturable photoexcited-carrier refraction (SPCR). As mentioned previously, the nonlinearity originates from the carrier population difference. Given a pulse of an arbitrary pulse duration that impinges on the system, the maximum excited carrier density is reached at the peak of the pulse. If the pulse duration is shorter than the system’s relaxation constant i.e., τ1~113 fs, then the maximum carrier density is reached on the time-scale of the pulse duration, the carriers then remain in the excited state even after the pulse passes, subsequently relaxing on a time-scale of τ1. However, if the pulse duration is longer than τ1 then carriers continuously undergo excitation and relaxation as the pulse passes with the carrier population difference continuously evolving, and therefore the optical nonlinearity becomes dependent on the duration of the pulse. The saturability in graphene deviates from saturability in other 2D materials due to the presence of its unique gapless band structure which facilitates spontaneous saturation near the Dirac point even when there is no field23. Therefore, it is apt that we refer to the Kerr-type nonlinearity characterised using the Z-scan method as n2,eff due to the presence of this contributing mechanism.
Conclusions
The systematic measurement and analysis of the dependence of n2,eff on the spectral and temporal properties of the pulse, has allowed us to gain a more fundamental understanding of the parameters governing the observed nonlinear optical effect in graphene. This sheds significant light on the widespread debate in the field regarding the large variation in the n2,eff value for graphene due to varying experimental conditions and sample preparation techniques. The dependence of n2,eff on the exciting wavelength revealed a quadratic (n2,eff ∝ λ2) relationship observed experimentally and confirmed theoretically. The quantum theory developed can be used to calculate the nonlinear response under varying the relaxation coefficients and Fermi energy, and the results can be extended to other spectral regions. The time-resolved Z-scan measurement revealed that the heating and cooling dynamics within our graphene sample are simply too fast to be probed with ~100 fs pulses using this method. However, this method reveals a practical application in all-optical ultrafast switching of the nonlinearity, completely controlled by the pulse-duration and power of the impinging laser pulse.
Through the pulse-duration dependent measurement, we were able to confirm the theoretically predicted relationship between n2,eff and the laser pulse-duration in the hundreds of femtosecond regime, with n2,eff growing larger with longer pulse-duration. Our results also coincide with the trend that is observed over several papers4,5,11,14 performing the measurement with different pulse durations, further reconciling our measurements, theory and experiments. In our measurements we used a prism-pair set-up to expand the pulses which is highly sensitive to beam alignment, posing a challenge if the pulse duration needs to be changed dynamically. Alternatively, transmission diffraction gratings can provide large pulse expansion ratios with high efficiencies and easier alignment34. Using the diffraction gratings a larger range of pulse durations can be scanned and a decisive relationship between n2,eff and pulse duration can be established.
Throughout all our experiments, the value for n2,eff remains positive. The sign of n2,eff has been a constant point of disagreement in literature, with the sign alternating from positive to negative depending on the method of characterisation employed or the conditions of the experiment. Theoretical studies have revealed that n2,eff is very sensitive to the Fermi energy of the sample3,17,18,21,22. Fermi energy modulation can be practically achieved with ease by electrically gating graphene samples in contrast to changing the spectral and temporal properties of the pulse to achieve the same tuning. Therefore, it becomes absolutely critical to perform an experimental characterisation of the dependence of n2,eff on Fermi energy. By scanning this parameter and observing the nonlinear response, it is possible to observe if or when the change in sign takes place, which would resolve the supposedly contradictory reports. With this study we have gained critical fundamental understanding of the underlying processes governing the nonlinear optical phenomena and the effect of experimental parameters which can be used to largely tune the effect.
Methods and Materials
Pump-probe integrated Z-scan measurement
The experimental set-up for this measurement is illustrated in Fig. 6. When operating in single beam mode, the set-up is a classic Z-scan measurement. The OA is used to normalise for absorption and laser fluctuations in the CA trace. In dual-beam mode, we use degenerate pump and probe at 900 nm, in a collinear configuration with a 20:1 pump/probe ratio. The pump and probe are orthogonally polarised using a λ/2 waveplate (λ/2), polarising beam-splitter (P-BS) and polariser (Pol1) before the sample. An analyser polariser (Pol2) placed after the sample is rotated to achieve extinction of the pump beam.
Pump-probe integrated Z-scan set-up (PPZS). The source is Ti:sapphire tunable laser capable of emitting from 690 to 1050 nm at a repetition rate of 80 MHz at ~100 fs. The laser has a variable high power attenuator on exit comprising of a half-waveplate (λ/2(780)) and a Glan-laser polariser (GP). The beam is directed by silver mirrors (M) into another half-waveplate (λ/2(900)) and polarising beamsplitter (P-BP) to prepare the orthogonal pump (transmitted) and probe (reflected) beams. Both beams are then directed through the dual-frequency chopper (Chp). The pump is directed into a small static retroreflector (Refl-S), while the probe is directed through a polariser (Pol1) and a large retroreflector (Refl-L) that is mounted on a translation stage that allows for one beam to be delayed relative to another. Upon return, both beams are combined at a pellicle beamsplitter (Pel) and guided to the Z-scan set-up. Both beams are then focused using an achromatic doublet lens (ADL) and impinge upong the graphene on quartz sample (GoQ), followed by another polariser (Pol2) which is oriented parallel to Pol1 for extinction of the pump beam. The beam is then bisected in the far-field by an non-polarising beamsplitter (NP-BP) with the reflected arm directed into the open aperture (OA) detector and the transmitted arm directed through an adjustable aperture (AP) into the closed aperture (CA) detector. For all Z-scan based measurements, single-beam or temporal, the power meter is utilised for data acquisition. In pump-probe mode the chopper and Lock-in amplifier are used for data acquisition.
The normalised CA transmittance is fitted to the equation: \(T(x,{{\rm{\Delta }}{\rm{\Phi }}}_{0})\simeq 1-\frac{4{{\rm{\Delta }}{\rm{\Phi }}}_{0}x}{({x}^{2}+9)({x}^{2}+1)}\), where x is the Rayleigh length (zR) normalised position (z/zR) and ΔΦ0 is the nonlinearity induced phase shift. When a pulsed source is used with pulse-width comparable to the duration of the nonlineairty, the nonlinear refractive index is extracted via \({n}_{2}=\frac{\sqrt{2}{{\rm{\Delta }}{\rm{\Phi }}}_{0}}{{k}_{0}{I}_{0}{L}_{eff}}\), where k0 is the wave vector, I0 is the on-axis irradiance and Leff is the effective length of the sample35. In our analysis the value for ΔΦ0 is extracted using a nonlinear least-squares curve fitting routine in MATLAB. The routine takes in the aforementioned function along with a starting value for ΔΦ0, and a vector constraining the upper and lower bound for the value. The routine then works to find a minimum for the sum of squares of the input function in an iterative manner, with the allowed number of iterations being easily modified. In our measurements the value for ΔΦ0 falls in the range of [−0.04, −0.15], which was the upper and lower bound input, while a starting point of 0 with 5000 iterations generally allowed for convergence.
Sample characterisation
In order to verify the quality of the samples, graphene on quartz (GoQ) samples (1 × 1 cm2) were characterised by Raman spectroscopy, shown in Fig. 1a. The samples were purchased from an external supplier and were fabricated using chemical vapour deposition (CVD) onto a large copper sheet. The copper sheet was then cut into the respective sample size and graphene was transferred from the copper onto the quartz substrate. The Raman spectroscopy was performed using a home-built set-up, combining a 561 nm continuous wave (CW) laser and a high-resolution spectrometer. Prior to every measurement the laser input was read to normalise the spectral data to output the Raman shifts. The D band, G band and 2D band peaks appear at 1328 cm−1, 1576 cm−1 and 2661 cm−1 respectively. The D band signifies disorder in the graphene lattice and is typically weak in high quality graphene, as seen in our sample measurement. A point to note as it pertains to the D band is that it is a resonant band and has very weak modes underlying it. The shape and position of this band can vary significantly depending on the excitation laser wavelength. The G band is a signature of an in-plane vibrational mode stemming from the stretching of the C-C bond, characteristic to all sp2 carbon systems. The 2D band is the second overtone of the D band and is the result of a two-phonon lattice vibrational process. It is always strong in graphene and does not represent defects regardless of the presence of the D band. The peak at ~2460 cm−1 has been referred to as the G* band and is attributed to a double resonance36. The peak appearing at ~2325 cm−1 may arise from additional defects or resonances. The relative intensities of the 2D and G peaks confirm that the sample is single layer.
We also perform a temporal correlation measurement on the sample, shown in Fig. 1b. The measurement was performed in the dual-beam mode of the PPZS set-up using the translation stage and cross polarisers to obtain extinction of the pump. An extinction of ~10−4 was achieved with this configuration. The pump/probe power ratio was kept at 20:1, with the pump power being 200 mW. Due to the short time-scale of the temporal correlation of the two pulses, a stage capable of achieving a repeatable resolution of ~5 femtosecond was employed. Lower resolution could be reached but was seen to be unreliable for a mechanical stage. The data is obtained over a time-scale of 1.5 picoseconds, limited by speed of the stage and the oscilloscope sampling rate. The data is fit to a single exponential function of the form: exp(t/τ), to obtain a τ1 relaxation time constant of about ~113 fs.
Theoretical modelling of the nonlinear optical response in graphene
The nonlinear response coefficients have been calculated via Semiconductor Bloch Equations (SBEs). In the continuous excitation regime, the optical response can be estimated based on the dynamics of (i) the microscopic population difference \({\mathscr{N}}({\bf{k}},t)\) and (ii) the microscopic polarization \({\mathscr{P}}({\bf{k}},t)\). In a moving frame {τ, k′} = {t, k − δk(t)}, where δk obeys \(\frac{\partial \delta {\bf{k}}}{\partial t}+{\rm{\Gamma }}\delta {\bf{k}}=-\frac{e}{\hslash }{\bf{E}}(t)\) and Γ is an phenomenological intraband relaxation coefficient, the dynamics of the charge carriers is governed by:
where \({\rm{\Phi }}({\bf{k}},t)=\frac{e{\bf{E}}\cdot {\hat{\phi }}_{{\bf{k}}}}{\hslash k}\) is the matrix element of the external potential of the direct optical transition, and the unit vector \({\hat{\phi }}_{{\bf{k}}}\) is defined as \({\hat{\phi }}_{{\bf{k}}}=\hat{z}\times {\bf{k}}/k\). The frequency \(\hslash {\varpi }_{{\bf{k}}}=2{ {\mathcal E} }_{{\bf{k}}}\) is the energy difference between the energy levels of the conduction and valence bands. At \(t=0\) before the electromagnetic field being applied, the population difference \({\mathscr{N}}\) is relaxed at its equilibrium \({{\mathscr{N}}}_{eq}=f(\hslash {v}_{F}k)-f(-\hslash {v}_{F}k)\) where \(f\) is Fermi-Dirac distribution function. The moving frame accounts for intraband dynamics which has significant contribution in high harmonic generation via coherent Bloch oscillations.
Since the crystalline structure of graphene is centrosymmetric, even order nonlinearities are prohibited and therefore the first nonlinear term is the third order. We describe the effect of this third order nonlinearity by considering three complex fields with the time dependence of \({e}^{i{\omega }_{p}t}\), \({e}^{i{\omega }_{q}t}\) and \({e}^{i{\omega }_{r}t}\) and their mixing through the third order conductivity of graphene. The third order optical response can be interpreted as a three-photon process and different terms contribute to the third order conductivity tensor namely pure intraband term, pure interband term and combination of the both. There are six distinct photon processes contributing to the third order optics of graphene. However, since intraband processes mostly concern harmonic generation, in optical range the interband process plays the leading role in Kerr type linearity. SBEs can be combined and recast in the form of a damp-driven harmonic oscillator equation. The distinctive nonlinear process can be then obtained using an iterative technique23.
The conductivity tensors for the six distinct photon processes contributing to the third order optical effect in graphene are presented in the supplemental document. The leading term (purely interband term) is:
where \({{\mathscr{P}}}_{I}\) denoted the intrinsic permutation operator and the operators \({{\mathscr{V}}}_{{\bf{k}}}\) and \({{\mathscr{W}}}_{{\bf{k}}}\) are defined as:
The equivalent third order bulk susceptibility of graphene is related to the third order surface dynamic conductivity via:
where dgr is the equivalent thickness of graphene which is typically around d ≈ 0.3 nm3 and ε0 is the free space permittivity.In the case of graphene, the definition of the nonlinear bulk susceptibility is ambiguous due to the arbitrariness in the definition of the thickness of the two-dimensional structure. The Kerr coefficient is defined through the intensity dependent refractive index i.e. n = n0 + (n2 − ik2)I where I = 2ε0Re{n0}c|E|2 (c is the speed of light). The complex nonlinear coefficient n2−ik2 is related to the bulk susceptibility χ(3)(ω, ω, −ω) as3:
Since bulk susceptibility and the linear refractive index n0 are both normalized to the thickness dgr, the Kerr coefficient is less sensitive to a particular selection for the thickness of the 2D material. The estimated values for the Kerr coefficient of graphene and the expected spectral dependence are presented in supporting information document.
Data Availability
Experimental data presented in this article is available from the corresponding author upon request.
References
Wallace, P. R. The band theory of graphite. Phys. Rev. 71, 622–634, https://doi.org/10.1103/PhysRev.71.622 (1946).
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Sci. 306, 666–669, https://doi.org/10.1126/science.1102896 (2004).
Semnani, B., Majedi, A. H. & Safavi-Naeini, S. Nonlinear quantum optical properties of graphene. J. Opt. 18, 035402, https://doi.org/10.1088/2040-8978/18/3/035402 (2016).
Hendry, E., Hale, P. J., Moger, J., Savchenko, A. K. & Mikhailov, S. A. Coherent nonlinear optical response of graphene. Phys. Rev. Lett. 105, 97401, https://doi.org/10.1103/PhysRevLett.105.097401 (2010).
Zhang, H. et al. Z-scan measurement of the nonlinear refractive index of graphene. Optics Letters 37, 1856, https://doi.org/10.1364/OL.37.001856 (2012).
Krishna, M. B. M., Kumar, V. P., Venkatramaiah, N., Venkatesan, R. & Rao, D. N. Nonlinear optical properties of covalently linked graphene-metal porphyrin composite materials. Appl. Phys. Lett. 98, 081106, https://doi.org/10.1063/1.3553500?journalCode=apl (2011).
Ciesielski, R. et al. Graphene near-degenerate four-wave mixing for phase characterization of broadband pulses in ultrafast microscopy. Nano Lett. 15, 4968–4972, https://doi.org/10.1021/acs.nanolett.5b00893 (2015).
Jiang, T. et al. Gate-tunable third-order nonlinear optical response of massless dirac fermions in graphene. Nat. Photonics 12, 430–436, https://doi.org/10.1038/s41566-018-0175-7 (2018).
Vermeulen, N. et al. Negative kerr nonlinearity of graphene as seen via chirped-pulse-pumped self-phase modulation. Phys. Rev. Appl. 6, 044006, https://doi.org/10.1103/PhysRevApplied.6.044006 (2016).
Vermeulen, N. et al. Graphene’s nonlinear-optical physics revealed through exponentially growing self-phase modulation. Nat. Commun. 9, 2675, https://doi.org/10.1103/PhysRevApplied.6.044006 (2018).
Chen, W. et al. The nonlinear optical properties of coupling and decoupling graphene layers. AIP Adv 3, 042123, https://doi.org/10.1063/1.4802889 (2013).
Miao, L. et al. Broadband ultrafast nonlinear optical response of few-layers graphene: toward the mid-infrared regime. Photonics Res. 3, 214–219, https://doi.org/10.1364/PRJ.3.000214 (2015).
Demetriou, G. et al. Nonlinear optical properties of multilayer graphene in the infrared. Opt. Express 24, 13033–13043, https://doi.org/10.1364/OE.24.013033 (2016).
Dremetsika, E. et al. Measuring the nonlinear refractive index of graphene using the optical kerr effect method. Opt. Lett. 41, 3281–3284, https://doi.org/10.1364/OL.41.003281 (2016).
Ahn, K. J. et al. Wavelength and fluence-dependent third-order optical nonlinearity of mono- and multi-layer graphene. Appl. Opt. 56, 9920–9924, https://doi.org/10.1364/AO.56.009920 (2017).
Soh, D. B. S., Hamerly, R. & Mabuchi, H. Comprehensive analysis of the optical kerr coefficient of graphene. Phys. Rev. A 94, 023845, https://doi.org/10.1103/PhysRevA.94.023845 (2016).
Ooi, K. J., Ang, L. K. & Tan, D. T. Waveguide engineering of graphene’s nonlinearity. Appl. Phys. Lett. 105, 111110, https://doi.org/10.1063/1.4895934 (2014).
Cheng, J., Vermeulen, N. & Sipe, J. Numerical study of the optical nonlinearity of doped and gapped graphene: From weak to strong field excitation. Phys. Rev. B 92, 235307, https://doi.org/10.1103/PhysRevB.92.235307 (2015).
Mikhailov, S. A. & Ziegler, K. Nonlinear electromagnetic response of graphene: frequency multiplication and the self-consistent-field effects. J. Physics: Condens. Matter 20, 384204, https://doi.org/10.1088/0953-8984/20/38/384204/meta (2008).
Zhang, Z. & Voss, P. L. Full-band quantum-dynamical theory of saturation and four-wave mixing in graphene. Opt. Lett. 36, 4569–4571, https://doi.org/10.1364/OL.36.004569 (2011).
Cheng, J. L., Vermeulen, N. & Sipe, J. E. Third order optical nonlinearity of graphene. New J. Phys. 16, 053014, https://doi.org/10.1088/1367-2630/16/5/053014/meta (2014).
Chatzidimitriou, D., Pitilakis, A. & Kriezis, E. E. Rigorous calculation of nonlinear parameters in graphene-comprising waveguides. J. Appl. Phys. 118, 023105, https://doi.org/10.1063/1.4926501 (2015).
Semnani, B. et al. Anomalous optical saturation of low-energy dirac states in graphene and its implication for nonlinear optics. 2D Mater. 6, 031003, https://doi.org/10.1088/2053-1583/ab1dea (2019).
Berciaud, S., Ryu, S., Brus, L. E. & Heinz, T. F. Probing the intrinsic properties of exfoliated graphene: Raman spectroscopy of free-standing monolayers. Nano Lett. 9, 346–352, https://doi.org/10.1021/nl8031444 (2009).
Ogusu, K. & Shinkawa, K. Optical nonlinearities in silicon for pulse durations of the order of nanoseconds at 1.06 μm. Opt. Express 16, 14780–14791, https://doi.org/10.1364/OE.16.014780 (2008).
Liu, Z. et al. Nonlinear optical properties of graphene oxide in nanosecond and picosecond regimes. Appl. Phys. Lett. 94, https://doi.org/10.1063/1.3068498 (2009).
Meng, F. et al. Saturable absorption of femtosecond optical pulses in multilayer turbostratic graphene. Opt. Express 24, 15261–15273, https://doi.org/10.1364/OE.24.015261 (2016).
Sheik-Bahae, M., Said, A. A. & Stryland, E. W. V. High-sensitivity, single-beam n 2 measurements. Opt. Lett. 14, 955–957, https://doi.org/10.1364/OL.14.000955 (1989).
Wang, J., Sheik-Bahae, M., A. A. Said, D. J. H. & Stryland, E. W. V. Time-resolved z-scan measurements of optical nonlinearities. J. Opt. Soc. Am. B 11, 1009–1017, https://doi.org/10.1364/JOSAB.11.001009 (1994).
Malic, E., Winzer, T., Bobkin, E. & Knorr, A. Microscopic theory of absorption and ultrafast many-particle kinetics in graphene. Phys. Rev. B 84, 205406–1–14, https://doi.org/10.1103/PhysRevB.84.205406 (2011).
Sherriff, R. E. Analytic expressions for group-delay dispersion and cubic dispersion in arbitrary prism sequences. J. Opt. Soc. Am. B 15, 1224–1230, https://doi.org/10.1364/JOSAB.15.001224 (1998).
Johannsen, J. C. et al. Tunable carrier multiplication and cooling in graphene. Nano Lett. 15, 326–331, https://doi.org/10.1021/nl503614v (2015).
Nikolakakos, I., Major, A., Aitchison, J. & Smith, P. Broadband characterization of the nonlinear optical properties of common reference materials. IEEE J. Sel. Top. Quantum Electron. 10, 1164–1170, https://doi.org/10.1109/JSTQE.2004.836007 (2004).
Bonod, N. & Neauport, J. Diffraction gratings: from principles to applications in high intensity lasers. Advances in Optics and Photonics 8, 156–199, https://doi.org/10.1364/AOP.8.000156 (2016).
Sheik-Bahae, M., Said, A. A., Wei, T.-H., Hagan, D. J. & Stryland, E. W. V. Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quantum Electron. 26, 760–769, https://doi.org/10.1109/3.53394 (1990).
Zolyomi, V. & Koltai, J. Kurti Resonance raman spectroscopy of graphite and graphene. Phys. Status Solidi B 248, 2435–2444, https://doi.org/10.1002/pssb.201100295 (2011).
Acknowledgements
S.T., B.S. and A.H.M. acknowledge the financial support received from the Natural Science and Engineering Research Council of Canada (NSERC) and internal funding from U.W. B.S. and S.S.N. also acknowledge the financial support provided by the Canada First Research Excellence Fund.
Author information
Authors and Affiliations
Contributions
S.T., B.S., and A.H.M. defined the project and conceived the experiment(s). S.T. and B.S. conducted the experiment(s), B.S. developed the theoretical model and S.T. analyzed the results, under the guidance of A.H.M. and S.S.N. S.T. and B.S. wrote the manuscript and all authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
41598_2019_46710_MOESM1_ESM.pdf
Supporting Information - Experimental Characterization of Ultrafast, Tunable and Broadband Optical Kerr Nonlinearity in Graphene
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Thakur, S., Semnani, B., Safavi-Naeini, S. et al. Experimental Characterization of the Ultrafast, Tunable and Broadband Optical Kerr Nonlinearity in Graphene. Sci Rep 9, 10540 (2019). https://doi.org/10.1038/s41598-019-46710-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-019-46710-x
This article is cited by
-
Kerr nonlinear effect in the graphene-based wedged hybrid plasmonic waveguide
Optical and Quantum Electronics (2024)
-
Comparative Study of Rogue Wave Solutions for Autonomous and Non-autonomous Saturable Discrete Nonlinear Schrödinger Equation
International Journal of Theoretical Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.