Introduction

Mixtures of light elements at extreme pressure and temperature conditions exhibit intriguing chemical and physical processes, involving complex bonding configurations. Of particular interest are mixtures of water (H2O), methane (CH4), and ammonia (NH3), also called planetary “ices”, as they comprise the major components of the interiors of the ice giant planets Uranus and Neptune. It is commonly assumed that they consist of an outer hydrogen-helium layer, an “icy” mantle, and possibly a rocky core1,2,3. As pressure and temperature increase from the outer layers towards the core, icy mixtures are expected to lose their original molecular nature and to exhibit a wide range of different states embracing atomic, molecular, and dissociated fluids, plasmas, and superionic lattices4,5. In more detail, the term “ice” refers to unspecified high-pressure phases of mixtures whose exact composition is unclear as discussed in previous work2,3.

The complex behaviour of these mixtures at planetary interior conditions – pressures of several megabar (1 Mbar = 100 GPa) and temperatures of a few thousand Kelvin – is at the basis of several gaps in our understanding of Uranus and Neptune. Their internal structures are inferred from the observed gravitational fields, masses, rotational velocities, and radii. However, their mass distributions remain ambiguous, especially in their deep interiors3,6. An accurate analysis of the Voyager 2 data7,8,9,10 even opens the possibility for a dichotomy in their structures, indicating that the two planets could have different internal structures and thermal histories despite being similar in mass and radius. Indeed, the data suggest an internal heat source for Neptune, while Uranus’ low luminosity indicates that it is presently in thermal equilibrium with the radiation received from the Sun11,12. Moreover, our lack of precise information on transport properties of the planetary ices such as conductivities is casting serious issues in explaining Uranus and Neptune’s non-dipolar, non-axisymmetric magnetic fields13. While it is customarily assumed that their peculiar structure is due to the fact that they originate in a thin outer shell, it is not clear if the main contribution to the planetary dynamo is given by hydrogen, which is present in the atmosphere and becomes metallic at around 1 Mbar3,14, or by the icy mixture in the deep interiors15,16. Resolving this situation is even more urgent today, given that the number of known exoplanets keeps growing steadily with lots of them similar in size and radius to Uranus and Neptune. Since solar planets are used as prototypes for extrasolar planets17, the loose description of planetary ices and the resulting approximate portrait of Uranus and Neptune not only prevent the understanding of extrasolar giant planets such as GJ 436 b or HAT-P-11b but also affects our capability to distinguish Earth-like candidates. As a result, there is a great need to establish benchmarking values for the equations of states, phase diagrams, and transport properties of H2O-CH4-NH3 mixtures at megabar pressures and temperatures of a few thousand Kelvin.

So far, our knowledge of icy mixtures relies on Density Functional Theory Molecular Dynamics (DFT-MD) calculations and on few experimental data. DFT-MD calculations have provided equations of state, pair distribution functions, and bond autocorrelation functions5,18,19,20, allowing to deduce the structural (such as compressibility) and transport (such as viscosity) properties of the icy mixtures. The available experimental works have primarily characterised the equation of state and electrical conductivity, using single-shock compression – thus exploring thermodynamic conditions along the principal Hugoniot curve5,21,22, or double-shock compression, which allowed to probe lower temperatures5,22. However, existing experimental data are limited to 0.8 Mbar along the principal Hugoniot curve and 2.2 Mbar off the Hugoniot, missing temperature and reflectivity measurements. Pure water, on the contrary, has been compressed up to higher pressures23,24,25,26,27,28,29, along the principal, statically pre-compressed, and the ice VII Hugoniot curves. Moreover, the water shock-front reflectivity has been measured in the metallic regime25,26,27,28, whereas similar data are not available for icy mixtures.

In the present work, using laser-driven shocks we have compressed pure water, a water-ethanol mixture (WEM), and a water-ethanol-ammonia “synthetic planetary mixture” (SPM) representative for the interiors of Uranus and Neptune and similar to the previously studied “synthetic Uranus”22. We have measured the thermodynamic state of the shocked sample and the optical reflectivity of the shock front up to a pressure of 2.6 Mbar using standard rear-side optical diagnostics: two Doppler velocity interferometers (VISAR), a VISAR-independent reflectivity measure, and a streak optical pyrometer (SOP).

Methods and Experimental Setup

Pure water, a water-ethanol mixture, and a water-ethanol-ammonia mixture have been studied in order to characterise the behaviour of mixtures of various compositions and to isolate possible effects due to different chemical environments linked to the presence of carbon and nitrogen atoms. The water-ethanol mixture (WEM) is composed of 49.45% pure water and 50.55% pure ethanol in mass ratios, which correspond to the atomic abundance ratios of H:C:N:O = 22:4:0:7. The water-ethanol-ammonia synthetic planetary mixture (SPM) has been prepared by adding up pure water, pure ethanol, and a liquid water-ammonia (28% wt.) mixture with the following mass ratios: 23.26% of water, 46.23% of ethanol, 30.51% of water-ammonia solution. The following atomic ratio has been obtained: H:C:N:O = 25:4:1:7, with the aim of reproducing the chemical composition of Uranus’ and Neptune’s mantles. The C:N:O abundance ratios are comparable to those of the Solar System30. Ethanol has been preferred over methane as component of the mixture to avoid demixing issues. The refractive index at 532 nm has been measured for both mixtures as \({n}_{0}^{{\rm{S}}{\rm{P}}{\rm{M}},{\rm{W}}{\rm{E}}{\rm{M}}}\,=1.36\). The values at 1064 nm have been extrapolated using the same wavelength dependence of the refractive index as that of water. The densities of the mixtures at ambient conditions are \({\rho }_{0}^{{\rm{SPM}}}=0.889\) g/cm3 and \({\rho }_{0}^{{\rm{WEM}}}=0.881\) g/cm3.

Experiments were performed at the GEKKO XII laser facility (Institute of Laser Engineering, Osaka University, Japan)31 and at the LULI2000 laser facility (École Polytechnique, France). At GEKKO XII, 3 up to 9 beams (corresponding to energies on target from 120–440 J) at 351 nm have been used, with a 600 μm focal spot diameter. At LULI2000, 1 or 2 beams (energies on target from 200–500 J) at 527 nm have been used, with a 500 μm focal spot diameter. In both cases, the laser pulse duration was 2.5 ns and phase plates were used to obtain a uniform irradiation spot. As rear-side probe lasers, a YAG at 532 nm was used at GEKKO XII with a full-width half-maximum pulse duration of ~10 ns and a YAG at 532 and 1064 nm was used at LULI2000, with a full-width half-maximum pulse duration of ~20 ns.

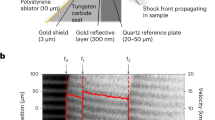
To optimise the target design and ensure there were no shock reverberations in the sample, the laser-target interaction and the shock loading into the cell have been simulated with the Lagrangian 1-D hydrodynamic code MULTI32. The equation of state of the target components have been extracted from the SESAME tables33,34. The table 7154 for water has been used for the mixtures. The multi-layered target cells were composed of a 10–15 μm thick polystyrene ablator, a 40 μm thick aluminium shield, a 50 μm thick α-quartz standard, the sample (4 mm thick), and a rear α-quartz window (200 μm thick). We also performed some high-intensity shots at GEKKO XII with 50 μm of polystyrene/3 μm of gold/5 μm of aluminium/20 μm of α-quartz/4 mm of sample/200 μm of α-quartz targets. The gold layer served as X-ray shield to prevent any pre-heating of the sample. Detailed information about the target cells can be found in the Supplementary information.

A decaying shock technique has been employed. In this approach, the laser pulse is designed to produce a strong shock that decays in time. As the shock propagates in the sample, each successive layer is compressed at a different pressure-temperature condition on the principal Hugoniot curve. As long as the optical depth of the loaded state is lower than the longitudinal temperature gradient length scale, the collected self-emission can be considered as originating from a thin layer behind the shock front, thus allowing a temperature measurement of the Hugoniot states loaded by the shock35,36.

The time-resolved shock velocity Us(t) starting from the shock arrival time in the quartz sample \(t={t}_{1}\) has been extracted using the Neutrino software37 from the output of the two VISARs38 (see the Supplementary information), both working at 532 nm (GEKKO XII) or working one at 532 and one at 1064 nm (LULI2000). The VISAR velocity-per-fringe parameters were 4.476 and 7.432 km/s at GEKKO XII, 15.94 and 6.08 km/s at LULI2000. The thermodynamic conditions (the mass density ρ, the pressure p, and the internal energy density E) reached in the mixture at the moment of the shock arrival have been obtained from the Rankine-Hugoniot relations39,40 through impedance mismatch41, using quartz as in-situ standard. Impedance mismatch requires the measure of the shock velocities (\({U}_{s}^{{\rm{Qz}}}\) and \({U}_{s}^{{\rm{sample}}}\) right before and after the time \(t={t}_{2}\) when the shock crosses the quartz/mixture interface. We were able to extract \({U}_{s}^{{\rm{Qz}}}\) and \({U}_{s}^{{\rm{sample}}}\) from the time-dependent shock velocity Us(t) via an extrapolation to t2 of a linear fit on a 1–2 ns time window ending 100–200 ps before (for \({U}_{s}^{{\rm{Qz}}}\)) or beginning 100–200 ps after (for \({U}_{s}^{{\rm{sample}}}\)) t2. Shock versus fluid (or particle) velocity (Us-Up) data from the Sandia Z-pinch facility42 have been used as reference for quartz. The adiabatic release of quartz on the lower-impedance mixture has been approximated using the mirror reflection of the quartz Hugoniot with respect to the line \({U}_{p}={U}_{p}^{Qz}\) in the p-Up plane. This approximation is validated since in this regime the entropy increase along a Hugoniot curve differs from an adiabatic path only at the third order in relative compression. We verified that this approximation agrees within the error bars with a Mie-Grüneisen release model43 in the region where the latter can be applied.

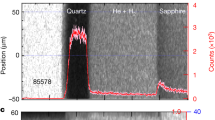
The time-resolved self-emission has been measured through a streaked optical pyrometer (SOP) working in a spectral range centred around \({\lambda }_{{\rm{S}}{\rm{O}}{\rm{P}}}=455\,{\rm{n}}{\rm{m}}\) with a FWHM of 20 nm. The time-resolved temperature of the states reached downstream the decaying shock has been obtained from Planck’s law \(T(t)={T}_{0}/\,{\rm{l}}{\rm{n}}[1+A{\varepsilon }_{532{\rm{n}}{\rm{m}}}\,(t)/{N}_{c}(t)]\), where \({T}_{0}=hc/{k}_{B}{\lambda }_{{\rm{S}}{\rm{O}}{\rm{P}}}\), A is a calibration factor, \({\varepsilon }_{455{\rm{n}}{\rm{m}}}\,(t)\) is the time-resolved emissivity of the shock front at the working wavelength and Nc(t) is the time-resolved number of counts on the SOP. To get the emissivity at 455 nm we used the reflectivity measured at 532 nm under a grey-body hypothesis: \({\varepsilon }_{455{\rm{n}}{\rm{m}}}\,(t)=1-{R}_{532{\rm{n}}{\rm{m}}}\,(t)\). This hypothesis introduces a negligible error source, since the temperature measures depend logarithmically on the emissivity and, as the measured reflectivity was often below 30%, a relative change in reflectivity is attenuated when \(\varepsilon =1-R\) is calculated. The SOP calibration has been made either in situ, by determining the A factor using quartz as standard (GEKKO XII), or using a calibration lamp with known emission temperature (LULI2000, see the Supplementary information). A typical VISAR and SOP output is shown in Fig. 1, together with the extracted shock velocity and self-emission temporal profiles.

Figure 1
figure 1

Diagnostics output of a typical shot on the SPM at the GEKKO facility. From top to bottom: VISAR image; SOP image; time-resolved shock velocity; time-resolved SOP counts. The three time intervals indicate when the probe laser is reflected by aluminium (Al), when a reflecting shock front is propagating through the quartz layer (Qz), and when the shock front is propagating through the mixture sample. The transverse target dimension is ~180 μm.

Full size image

The shock compression of the samples induces a refractive index change. According to the Fresnel equations, this implies that the shock front will reflect a fraction of the incident light from the probe laser. The time-resolved reflectivity of the shock front has been measured with the VISARs as the ratio between the shot signal and a reference signal reflected on the aluminium/quartz interface and normalised using the known relation between shock velocity and reflectivity in quartz at 532 nm44 and 1064 nm45. A time-resolved VISAR-independent reflectivity measurement at 532 nm (“reflectometer”) was included in the setup to corroborate the reflectivity measurements obtained from the VISAR fringe system.

The Hugoniot curves of the WEM and the SPM are reproduced by DFT-MD calculations using a Linear Mixing Approximation (LMA). The LMA is performed using the pure water, methane, and ammonia equations of state from DFT-MD simulations20. In particular, the WEM is modelled by a 7:4 water-methane mixture, while the SPM is represented by a 7:4:1 water-methane-ammonia mixture. A quantum correction to the internal energies has been added as motivated in previous work46. This correction typically yields much better agreement between simulation and experiment along the Hugoniot as has been shown for pure ammonia47. Since the stoichiometry of the mixtures in the simulations differs slightly from the experiment, the initial Hugoniot densities have been determined by performing additional DFT-MD calculations employing VASP48,49,50. Four to six density points have been computed along the 298 K isotherms for water, methane, ammonia, the 7:4 water-methane mixture, and the 7:4:1 water-methane-ammonia mixture. For the pure compounds, the same parameters as in a previous work20 have been used, while 88 and 96 molecules have been used for the binary and ternary mixture, respectively. The linear mixing approximation is found to agree within ±2 kJ/g in energy for both mixtures along the 298 K isotherm. In linear mixing densities differ from the real mixtures up to 6% and 3% for the binary and ternary mixture, respectively. Overall, these findings are within the range discussed in a previous work20, except the 6% discrepancy in density for the water-methane mixture, which is most likely due to well-known pressure-dependent solubility for this mixture51. Finally, initial densities of 0.7019 g/cm3 for the water-methane mixture and 0.7301 g/cm3 for the water-methane-ammonia mixture have been found at the pressures given by the experimentally used real mixtures containing ethanol.

Results and Discussion

Equation of state

Figure 2 (top) shows the Us-Up data for pure water, the WEM, and the SPM, together with previous results on the similar “synthetic Uranus”22. A linear fit on previous water data26, Us = (1.350 ± 0.014) \({U}_{p}+(2.16\pm 0.15)\,{\rm{km}}/{\rm{s}}\) is also shown. The corresponding figure for all available data on pure water is provided in the Supplementary information. The two water data points of this study are in perfect agreement, thus validating the experimental procedure. The obtained SPM data are also compatible within error bars with this linear fit. A satisfying agreement is also found for WEM except for two data points. Furthermore, Fig. 2 also presents DFT-MD calculations. For the water-methane and the water-methane-ammonia mixtures, the LMA has been used as discussed above. We find very good agreement between the experimental data and the simulations, suggesting a validation of the LMA approach along the Hugoniot curve.

Figure 2
figure 2

Top. Experimental shock - fluid velocity data on water, WEM, and SPM (blue, green, and red points with error bars, respectively) compared to DFT-MD calculations (triangles). A linear fit on previous water data26 and previous experimental data on synthetic Uranus22 (similar to the SPM) are shown for comparison. Bottom. Transposition in the pressure - compression factor (ρ/ρ0) plane of the data displayed on the top image. Other previous data on water23,24,27 and on synthetic Uranus21 are shown.

Full size image

Using the Rankine-Hugoniot equations, we extracted the ρ-p-(E − E0) thermodynamic conditions from the Us-Up relation. ρ-p-(E − E0) results are shown in Table 1. Pressure as a function of compression is shown on the bottom of Fig. 2 (see also the Supplementary information for a comparison with the calculations).

Table 1 Experimental data on pure water, WEM and the SPM.
Full size table

The temperature-pressure (T-p) relations of water and the considered mixtures are shown in Fig. 3, together with different temperature-pressure profiles predicted for Uranus20,52,53. Our data have been fitted with the quadratic function \(T(p)={T}_{{\rm{amb}}}+{c}_{1}p+{c}_{2}{p}^{2}\) (with \({T}_{{\rm{amb}}}=300\,{\rm{K}}\)). An extrapolation of our fit to lower pressures is compatible with previous gas-gun data24. While our data agree within the errors with recent laser shock results27, our temperatures are higher than those given by DFT-MD simulations54, although the discrepancy is reduced when quantum corrections from molecular vibrations are taken into account46 (the predicted temperatures increase of \(\simeq \)700 K). Our SPM results agree with a previous low-pressure experimental study of the very similar synthetic Uranus21. Although the relatively large error bars on temperature make the detection of possible discrepancies rather difficult, water, the WEM, and the SPM temperatures along the principal Hugoniot curves are comparable. We also notice that these findings are in agreement with our DFT-MD calculations using the LMA.

Figure 3
figure 3

From top to bottom: temperature - pressure relation for pure water (blue data) along the principal Hugoniot curve; the same relation for the WEM (green data) and the SPM (red data); temperature difference between the fit on mixtures and the fit on pure water. Each filled circle is a time-resolved measure during the propagation of a decaying shock. Each area corresponds to the error bars of the associated fit. Previous studies of pure water24,27,46,54 and synthetic Uranus21 are shown for comparison. Different Uranus interior models20,52,53 are shown in purple.

Full size image

The similar Us-Up and T-p relations between water and mixtures can be interpreted in light of previous DFT-MD simulations5, which identify the regime explored in this study as an electronically conducting phase. At these temperatures, carbon-carbon and carbon-nitrogen bond lifetimes are predicted to be very short19. Therefore phenomena like polymerisation and clustering are not expected to occur and the presence of carbon and nitrogen atoms should not influence the Us-Up and T-p relation of the SPM with respect to that of pure water. However, potentially existing chemical processes in the compressed bulk material could not be observed in this study, which relies on shock-front measurements. All over the studied range, our Us-Up and T-p data show very good agreement with LMA calculations, which validates this approximation at planetary conditions20.

The T-p data of this work are hereafter compared with the available models of planetary internal profiles. Most of them20,52 predict an adiabatic profile inside the icy giants, implying that temperatures stay relatively low (3000–4000 K) even at the highest pressures we explored. Nevertheless, adiabatic models are not consistent with Uranus‘ thermal evolution and more advanced internal structure models including a thermal boundary layer are suggested53. The internal profiles hence obtained are much hotter, spanning from 7000–14000 K. Our data therefore bring useful input for these models up to 1.5 Mbar. Moreover, the recent discovery of a large amount of exoplanets exhibits a wide range of structures including hot Neptunes, whose internal profiles can match the thermodynamical conditions we explored. Additionally, our data represent useful constraints for the validation of DFT-MD simulations at extreme conditions.

Shock-front reflectivity

The optical reflectivities R of the water, the WEM, and the SPM shock front at 532 nm and 1064 nm as a function of pressure (top) and temperature (bottom) are shown in Fig. 4. These are the first reflectivity measurements of this type of mixtures; moreover, no calculations of shock-compressed icy mixtures reflectivity exist in the literature to date. For all liquids, the gradual increase of reflectivity, from a low initial value of a few percent up to a saturation value of some ten percent, along the principal Hugoniot indicates a smooth transition from an insulating to an electronically conducting (“metallic”) state with the increase of density, pressure, and temperature.

Figure 4
figure 4

Reflectivity of water and the SPM at 532 nm (left) and 1064 nm (right) as a function of pressure (top) and temperature (bottom) along the principal Hugoniot curves. Top. Reflectivity vs pressure data. Blue, green, and red areas correspond to the fit of our data for pure water, WEM, and SPM within the error bars, respectively. Crosses are time-resolved measures during decaying shock propagation. Filled squares or circles correspond to previous DFT reflectivity calculations55 using the HSE and PBE exchange-correlation functionals, respectively. Previous data on water are shown for comparison26,27. Error bars are larger at 1064 nm because of the smaller number of available shots. Bottom. Reflectivity vs temperature data. Solid lines serve as guides to the eye.

Full size image

We performed a fit on each R-Us relation using a Hill function \(R({U}_{s})={R}_{0}+({R}_{sat}-{R}_{0})\cdot {U}_{s}^{k}\)/\(({U}_{s}^{k}+{U}_{0}^{k})\), which is suitable to model this gradual transition. The error bars of the fit are discussed in the Supplementary information and mainly depend on the calibration. The function has then been rescaled to be pressure-dependent using an experimentally determined equation of state for water26 and a fit on our data for the WEM and the SPM to link pressure and shock velocity. On the left we present a direct comparison between water, SPM and WEM at 532 nm while on the right the probe is at 1064 nm. Strong differences are observed in particular at 532 nm. The main one concerns the onset of reflectivity occurring in water at 1.1–1.2 Mbar while in SPM and WEM is observed at lower pressures, around 0.8 Mbar. The saturation values are also different (24% for water against 29% in SPM and even higher in WEM). Concerning water, our 532 nm reflectivity data are in quantitative agreement with previous experiments26,27. When compared with existing calculations55, at 532 nm, our reflectivity data suggest that the HSE exchange-correlation functional is more accurate than PBE, confirming what previous observations26. At 1064 nm, the differences are less important, which indicates a complex behaviour of optical conductivity that needs to be investigated with theoretical calculations in the future. We note that saturation values of reflectivity at 1064 nm for both liquids are greater than those at 532 nm. Water data at 1064 nm are in qualitative agreement with the calculations. Reflectivity data are also presented as a function of temperature (bottom of Fig. 4) showing a similar trend.

The fact that the onset pressure of the SPM and the WEM reflectivity at 532 nm occurs at pressures around 26% lower than in water cannot be fully explained by the 12% difference between their initial densities. The higher reflectivity of the mixtures may be due to a higher free electron density at the same thermodynamic conditions, as the ionisation energy of carbon-bearing molecules (e.g. 10.5 eV for ethanol) is lower than that of water (12.6 eV)56. This hypothesis seems to be corroborated by the reflectivity saturation values at 532 nm. Indeed they are 35% for the WEM, 29% for the SPM, and 24% for water, consistently ordered by carbon concentration.

Reflectivity data are essential due to their connection to electronic conductivity. In the literature, the extraction of the electronic conductivity from reflectivity data is often obtained using a classic or modified Drude model25,28. The assumptions of the Drude model in this regime are questionable, as water and mixtures are known not to follow a Drude behaviour for what concerns the frequency dependence of electronic conductivity. Nonetheless, it is insightful to use it to compare the conductivity water and the SPM. This way we estimate conductivity saturation values of 2200 and 3400 S/cm for water and SPM, respectively. The details of this estimation are presented in the Supplementary information.

Conclusions

In this work, pure water, a water-ethanol mixture (WEM), and a water-ethanol-ammonia “synthetic planetary mixture” (SPM) have been compressed by laser-driven decaying shocks up to a pressure of 2.73 ± 0.07, 2.79 ± 0.11, and 2.60 ± 0.08 Mbar, respectively. The thermodynamic states and shock-front reflectivities at 532 nm and 1064 nm have been measured along their principal Hugoniot curves. The datasets presented in this work significantly extend the previously reported results on icy planetary mixtures and provide constraints for theoretical discussions, e.g. by DFT-MD simulations.

The shock-fluid velocity relations for water, the WEM, and the SPM are comparable within the error bars. Their temperature-pressure relations are also comparable, although possible small discrepancies cannot be ruled out due to the error bars on the fitted relations. The performed LMA calculations of the Hugoniot curves of a water-methane and a water-methane-ammonia mixture suggest that the experimental data validate such an approach.

Pure water and mixtures exhibit different shock-front reflectivity behaviours. The pressure onsets of reflectivity for the WEM and the SPM are lower than that of water, while the reflectivity saturation values are higher for the SPM and WEM than for water. This may be a signature of the fact that carbon-rich mixtures dissociate at lower pressures and temperatures than pure water. Our data constitute thus a touchstone for the DFT-MD calculations of the structural and transport properties for complex mixtures with varying compositions of heavy elements. Finally, our reflectivity data show that the electronic conductivity of the SPM is larger than that of water. Such a result can have direct repercussions on planetary models including a thermal boundary layer53, where the electronic contribution is predominant with respect to the ionic one, due to the high temperatures involved.

Future experimental work should study high-pressure off-Hugoniot states to enlarge the explored scenario and probe thermodynamic conditions closer to those expected in planetary interiors. Pure liquid methane and pure liquid ammonia should be studied to provide a complete framework of the properties of the icy end-members and their mixtures. Finally, X-ray diffraction studies should be conducted on synthetic planetary ices to probe their bulk structure, thus overcoming the limitations of shock-front measurements.