Introduction

Network science is playing an increasingly significant role in many domains including physics, sociology, engineering, biology, management, and so on1. The heterogeneous nature of real networks2 asks for a crucial question: How to quantitatively measure a node’s importance in a dynamical process? Taking spreading dynamics as an example, a popular star in Twitter may remarkably accelerate a rumor and a few superspreaders could largely expand the epidemic prevalence of a disease3. Therefore, a good answer to the above question, namely an efficient algorithm to identify influential spreaders in complex networks, can help to better control the outbreak of an epidemic4, optimize the use of limited resources to facilitate the dissemination of information5, prevent catastrophic disruptions of power grid or the Internet6, discover the candidates of drug target and essential proteins7, and so on. Till far, most known methods only make use of the structural information8, which can be roughly classified into neighborhood-based centralities and path-based centralities.

Typical representatives of the neighborhood-based centralities are degree centrality9 (DC), H-index10 and k-shell decomposition method11 (KS). For DC, nodes with larger degrees are more influential. For H-index, nodes connecting with many large-degree neighbors are more influential. KS assigns a k-shell index to each node based on its topological location, where nodes closer to the core of the network will get higher k-shell indices, and nodes in the periphery will get lower k-shell indices. The nodes with higher k-shell indices are considered to be more influential. Besides, PageRank12 and LeaderRank13 are two representative neighborhood-based iterative methods, both suggesting that the influence of a node is determined by the influences of its neighbors. Two well-studied path-based centralities are closeness centrality14 (CC) and betweenness centrality15 (BC). CC claims that a node averagely closer to other nodes is more influential while BC assumes that a node locating in many shortest paths is of high influence.

Inspired by the gravity law, recently, Ma et al.16 proposed two gravity-law-based algorithms by considering both neighborhood information and path information (see Methods for the details of algorithms). Analogously, we proposed a variant algorithm named gravity model (GM), which also takes into account both neighborhood information and path information, where a node with larger degrees (neighborhood information) and averagely shorter distances to other nodes (path information) is more influential. Furthermore, we propose a local version of the gravity model (named as local gravity model, LGM for short) to lower the computational complexity and reduce the possible noise caused by interactions at distance. Such local model only accounts for pairwise interactions within a truncation radius. Empirical results show that GM and LGM perform very competitively in comparison with well-known state-of-the-art methods. In particular, for LGM, an empirically linear relation between the optimal truncation radius and the average distance of the network is observed.

Results

Algorithms

Individually speaking, nodes with large degrees are likely to be more influential. In addition, a node is of higher impacts on nearby nodes17. According to the above issues and inspired by the gravity law, we regard the degree of a node as its mass, and the shortest distance between two nodes as their distance. Hence a node i’s influence can be estimated as

$$S(i)=\sum _{j\ne i}\,\frac{{k}_{i}{k}_{j}}{{d}_{ij}^{2}},$$
(1)

where ki is the degree of node i, dij is the shortest distance between node i and node j, and j runs over all nodes other than i. Obviously, a node with many neighbors and be close to most nodes is more influential according to Eq. 1. Such method is named as gravity model as it adopts the formula of the gravity law.

Although GM can identify the nodes averagely closer to other nodes and with larger degrees, it has two shortcomings. Firstly, to calculate shortest distances between all node pairs is time-consuming for large-scale networks18. Secondly, in real propagation a node is hard to impact other nodes at distance and to estimate the interacting strength between distant nodes is usually inaccurate since the step-by-step decaying influence will be disturbed by accumulated noise19. Therefore, by introducing a truncation radius, we only consider the pairwise interactions within the truncation radius. Hence a node i’s influence can be estimated as

$${S}_{R}(i)=\sum _{{d}_{ij}\le R,j\ne i}\,\frac{{k}_{i}{k}_{j}}{{d}_{ij}^{2}},$$
(2)

where R is the truncation radius. Such method (Eq. 2) is named as local gravity model as it only takes into account local information of the network.

Data description

In this paper, fourteen real networks from disparate fields are used to test the performance of GM and LGM, including three collaboration networks (Jazz, NS and GrQc), four communication networks (EEC, Email, PG and Enron), four social networks (PB, Facebook, WV and Sex), one transportation network (USAir), one infrastructure network (Power) and one technological network (Router). Jazz20 is a collaboration network of jazz musicians. NS21 is a co-authorship network of scientists working on network science. GrQc22 is a collaboration network of eprint articles in arXiv categories General Relativity and Quantum Cosmology. EEC23 describes email interchanges between institution members of a large European research institution. Email24 describes email interchanges between users including faculty, researchers, technicians, managers, administrators, and graduate students of the Rovira i Virgili University. PG22 is a snapshot of the Gnutella peer-to-peer file sharing network from August 2002. Enron25 is the Enron email network. PB26 is a network of US political blogs. Facebook27 describes social circles from Facebook. WV28 is a network of Wikipedia who-votes-on-whom. Sex29 is a bipartite network in which nodes are females (sex sellers) and males (sex buyers) and links between them are established when males write posts indicating sexual encounters with females. USAir30 is the US air transportation network. Power31 is the power grid of the western United States. Router32 is a symmetrized snapshot of the structure of the Internet at the level of autonomous systems. These networks’ topological features (including the number of nodes, the number of links, the average degree, the average distance, the clustering coefficient31, the assortative coefficient33, the degree heterogeneity34 and the epidemic threshold35 of the SIR model36) are shown in Table 1.

Table 1 The basic topological features of the fourteen real networks.
Full size table

Empirical results

We apply the well-known SIR model36 to compare the rankings of influences produced by algorithms and simulations. Initially, one node (called seed) in the network is in the infected state (I) and the others are in the susceptible state (S). Each of the infected nodes can infect its susceptible neighbors with probability β. And in each step, every infected node changes to be recovered and will never participate in the dynamics with probability λ. The spreading process repeats until there are no more infected nodes in the network. The influence of any node i can be estimated by

$$F(i)={N}_{r}/N,$$
(3)

where Nr is the number of recovered nodes at the end of the dynamics. For simplicity, we set λ = 1, and the corresponding epidemic threshold34 is

$${\beta }_{c}\approx \frac{\langle k\rangle }{\langle {k}^{2}\rangle -\langle k\rangle },$$
(4)

where 〈k〉 and 〈k2〉 denote the average degree and the second-order moment of the degree distribution.

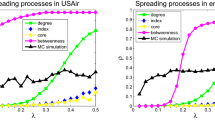
Given a network and the transmission probability β, to obtain the standard ranking of nodes’ influences, we implement 1000 independent runs, in each run every node is selected once as the seed once. The accuracy of an algorithm is measured by the Kendall’s Tau (τ)37 between the standard ranking and the ranking by the algorithm (see details in Methods). A larger value of τ means a stronger correlation between the two sequences and thus a better performance. Table 2 compares the accuracies of the two proposed algorithms (i.e., GM and LGM) and seven benchmark algorithms (see details about the benchmark algorithms in Methods). The transmission probability for each case is fixed as β = βc (for more values of β, see Fig. 1) and the parameters in relevant algorithms are all adjusted to their optimal values subject to the largest τ.

Table 2 The algorithms’ accuracies for β = βc, measured by the Kendall’s Tau (τ).
Full size table
Figure 1
figure 1

The algorithms’ accuracies for different β, measured by the Kendall’s Tau (τ).

Full size image

As shown in Table 2, both GM and LGM are very competitive. In particular, G+ and LGM perform best among the nine algorithms. Notice that, G+ also adopts the gravity formula16 (see Methods) but a node’s mass in G+ is defined as its k-shell index so G+ is indeed a global index. The results reported in Table 2 demonstrate the advantage of gravity models (e.g., G, G+, GM, LGM) and show that a local index (LGM) can outperform most benchmark algorithms including some global indices. As shown in Fig. 1, results for other values of β not too far from the threshold are consistent to the one at βc, suggesting the robustness of our findings.

Since to determine the optimal truncation radius, denoted by R*, asks for more computation, we want to see whether topological information can be used to profile R*. As shown in Fig. 2, R* approximately scales linearly with the average distance, as

$${R}^{\ast }\approx \frac{1}{2}\langle d\rangle $$
(5)

at β = βc. Such approximately linear relation also holds for other values of β not so far from βc. This empirical relation can save computational cost in practice.

Figure 2
figure 2

The relation between R* and 〈d〉 for β = βc. Fourteen pentagrams represent fourteen networks and the slope of the blue line is 1/2. The pentagram in black is the outlier – the Enron network. Although the optimal truncation radius R* = 7 is much different from what Eq. 5 predicts (i.e., R = 2), the algorithmic accuracy at R = 2 (τ = 0.4949) is very close to the best accuracy at R* = 7 (τ = 0.5075) in comparison with the traditional methods (e.g., about 0.34 for BC, 0.42 for CC and 0.46 for DC, KS and H-index). That is to say, to apply Eq. 5 can still achieve much better algorithmic performance than the traditional methods.

Full size image

Discussion

To measure influences of nodes in a certain networked dynamics, a straightforward method is to estimate the interacting strengths between node pairs in advance. The gravity law is a simple, elegant and representative formula that estimates the interacting strength between two nodes by simultaneously considering the intrinsic influences of the two nodes themselves and the distance between them. In this paper, the gravity model (Eq. 1) makes use of both the neighborhood information and the path information, which were separately adopted in many previous methods. Furthermore, to reduce the computational complexity and to avoid the accumulated noises through long paths, we proposed a local version of the gravity model (LGM, see Eq. 2). Both GM and LGM are very competitive, and of particular interests, the LGM requires less computation yet performs even better. Indeed, LGM is one of the two best-performed methods among many well-known benchmark algorithms.

A potential disadvantage of LGM is that it has a free parameter, namely the truncation radius R. The negative effects of the existence of R are twofold. Firstly, it asks for more computation to determine the optimal value of R. Secondly, if the optimal value, say R*, is very large, the computational complexity of LGM will be more or less the same to GM. Fortunately, as shown in Fig. 2, we found an empirical relation between R* and the average distance 〈d〉, so that if the computational resource is highly limited, we can use the relation (see Eq. 5) to approximate R*. In addition, since most real networks are of small-world property31,38, R* should be small and thus it requires much less computation than GM. Fortunately, the difference between two rankings of nodes produced by neighboring R will quickly converge to a very small value, so that to choose a small value of R will probably perform very well. In Table 3, we show the values of τ(R), which is the Kendall’s tau between two rankings of nodes’ influences with truncation radius being R and R + 1. One can observe that after R = 5, all networks are of τ(R) > 0.97 and a half of them are of τ(R) > 0.99. This indicates a strong saturation, namely the increasing of R will produce almost the same rankings if the value of R is already large.

Table 3 The Kendall’s Tau between two rankings of nodes’ influences produced by the LGM with truncation radius R and R + 1.
Full size table

Another similar model (named G+, see Eq. 11) shows very close performance to LGM. In comparison, LGM is more efficient since it completely depends on the local topological structure and thus can be calculated not only faster but also under the case where the global topology is not known. In the absence of global topology, G+ cannot be obtained since it sets a node’s k-shell index as its mass, and to determine the k-shell index needs the knowledge of the whole network. In despite the difference between G+ and LGM, the very good performance of G+ and LGM strongly suggest the validity and advantage of the usage of the gravity law to estimate the interacting strength. Of course, both G+ and LGM are very simple and general, which can be further improved by the following aspects (also leaving as open issues for future studies). Firstly, by introducing a few tunable parameters that can adjust the relative importance of mass and distance (e.g., to replace d2 by some da and/or to replace k by some kb) may result in more accurate predictions as indicated by known variants of the gravity law in other applications39. Secondly, we should explore how the topological features and dynamical processes affect the prediction accuracy and thus improve the original methods by introducing some topology-dependent and/or dynamics-sensitivity items40,41. Thirdly, the original gravity law is symmetric, while due to the different roles of different nodes or the essentially asymmetric nature of the dynamics42,43, the influence from node i onto node j could be different from the influence from node j onto node i, where an asymmetric form of the gravity law may be relevant.

Methods

The Kendall’s Tau

The Kendall’s Tau37 is an index measuring the correlation strength between two sequences. Considering two sequences with N elements, X = (x1, x2, …, xN) and Y = (y1, y2, …, yN). Any pair of two-tuples (x1, y1) and (xj, yj) (i ≠ j) are concordant if both xi > xj and yi > yj or both xi < xj and yi < yj. They are discordant if xi > xj and yi < yj or xi < xj and yi > yj. If xi = xj or yi = yj, the pair is neither concordant nor discordant. The Kendall’s Tau of two sequences X and Y can be calculated as

$$\tau =\frac{\mathrm{2(}{n}_{+}-{n}_{-})}{N(N-\mathrm{1)}},$$
(6)

where n+ and n− denote the number of concordant and discordant pairs, respectively. It can be seen that the extent to which τ exceeds zero indicates the strength of the correlation.

Benchmark centralities

Degree Centrality9 of node i is defined as

$$DC(i)=\sum _{j}\,{a}_{ij},$$
(7)

where A = {aij} is the adjacency matrix, that is, aij = 1 if i and j are connected and 0 otherwise.

H-index10 of node i, denoted by H(i), is defined as the maximal integer satisfying that there are at least H(i) neighbors of node i whose degrees are all no less than H(i). Such index is an extension of the famous H-index in scientific evaluation44 to network analysis.

Closeness Centrality14 of node i is defined as

$$CC(i)=\frac{N-1}{\sum _{j\ne i}\,{d}_{ij}}\mathrm{.}$$
(8)

Betweenness Centrality15 of node i is defined as

$$BC(i)=\sum _{s\ne i,s\ne t,i\ne t}\,\frac{{g}_{st}(i)}{{g}_{st}},$$
(9)

where gst is the number of shortest paths between nodes s and t, and gst(i) is the number of shortest paths between nodes s and t that pass through node i.

Gravity Centrality16 (G) of node i is defined as

$$G(i)=\sum _{j\in {\psi }_{i}}\,\frac{{k}_{s}(i){k}_{s}(j)}{{d}_{ij}^{2}},$$
(10)

where ks(i) is the k-shell index of node i, and ψi is the set of nodes whose distance to node i is less than or equal to 3.

Extended Gravity Centrality16 (G+) of node i is defined as

$${G}_{+}(i)=\sum _{j\in {{\rm{\Lambda }}}_{i}}\,G(j),$$
(11)

where Λi is the set of neighbors of node i.